超聲波電機夾心式定子結構含損耗機電等效電路建模與分析

董曉霄 黃肖肖 夏 博 袁 越

超聲波電機夾心式定子結構含損耗機電等效電路建模與分析

董曉霄 黃肖肖 夏 博 袁 越

（河海大學能源與電氣學院 南京 211100）

Langevin夾心式結構被廣泛應用于超聲波電機定子結構設計中，其壓電振子工作于厚度方向振動模態，現有等效電路模型由于沒有充分考慮壓電振子固有損耗特性，因此無法實現對機械品質因數的準確評估。為此，該文首先建立壓電振子含三類損耗的解耦機電等效電路模型，研究壓電振子三類固有損耗對機械品質因數的影響規律；再進一步建立Langevin夾心式結構的機電等效電路模型，分析材料特性參數和結構參數對于共振頻率、反共振頻率和有效機電耦合系數等關鍵性能指標的影響。最后制作Langevin夾心式結構性樣機，并分別對其阻抗-頻率特性和振動特性進行測試，通過實驗結論證實理論模型的準確性。該研究通過揭示壓電振子固有損耗對其輸出特性的差異性影響規律，為設計具有高機械品質因數的振子結構，并進一步開發高性能超聲波電機提供理論支撐。

超聲波電機 Langevin結構 機電等效電路 損耗

0 引言

超聲波電機是一種新型微特電機，其中Langevin換能器結構作為超聲波電機定子的常用結構[1-3]，具有機電轉換效率高[4]、功率容量大、靈敏度高、結構簡單、性能穩定[5-6]等優點。超聲波電機的研究方法通常包括有限元法[7-9]、解析法[10]和等效電路 法[11-15]，其中有限元法可以分析復雜的幾何結構，但其使用成本高，且無法充分地描述超聲波電機的電學特性；而運用解析法時，為了簡化建模，通常會引入一些假設條件，導致較大的誤差；相比之下，等效電路模型是利用機械振動和電路振蕩的相似原理，將壓電振子的機械諧振等效地轉化為電路諧振，可以有效地反映出壓電作動器的電學特性。文獻[11-13]通過建立等效電路模型，分析幾何結構對于換能器共振頻率、反共振頻率和有效機電耦合系數的影響；文獻[14]利用等效電路法分析振動體的材料特性對振動特性的影響；文獻[15]中利用等效電路法分析壓電換能器結構的阻抗頻率特性。上述文獻在等效電路建模時僅考慮介電損耗或機械損耗，對壓電損耗的考慮較少。然而，近幾年已有研究表明，壓電損耗在壓電陶瓷的熱量產生機制中具有關鍵的作用[16]。當前IEEE標準[17]中壓電振子等效電路模型僅考慮了壓電振子的機械損耗，該方法假定共振頻率處的機械品質因數與反共振頻率處的機械品質因數相等，但該結論與實驗結果相悖。

基于此，本文提出一種充分考慮壓電振子三類損耗的超聲波電機解耦機電等效電路模型，分別研究三類損耗對于機械品質因數的影響規律，并進一步對Langevin夾心式定子結構進行建模，研究結構參數和材料參數對其輸出特性的影響，最后，搭建實驗測試平臺，通過實驗測試對仿真結果進行驗證。

1 新型含損耗的機電等效電路模型

Langevin夾心式定子簡化結構如圖1所示，其中包括兩側的金屬結構和中間兩片以上疊堆的壓電陶瓷振子結構。壓電陶瓷振子沿厚度方向極化，兩片壓電陶瓷極化方向相反，中間側接正電壓，靠近金屬側接地，當向壓電振子施加交流電壓時，在垂直方向上產生振動，使兩個金屬端部產生縱向位移。

傳統Langevin機電等效電路模型如圖2所示，圖中，和分別表示電氣支路（即等效變壓器的一次側）的輸入電壓和電流。r1和r2為輸出力，r1和r2為機械分支（即等效變壓器的二次側）中的振

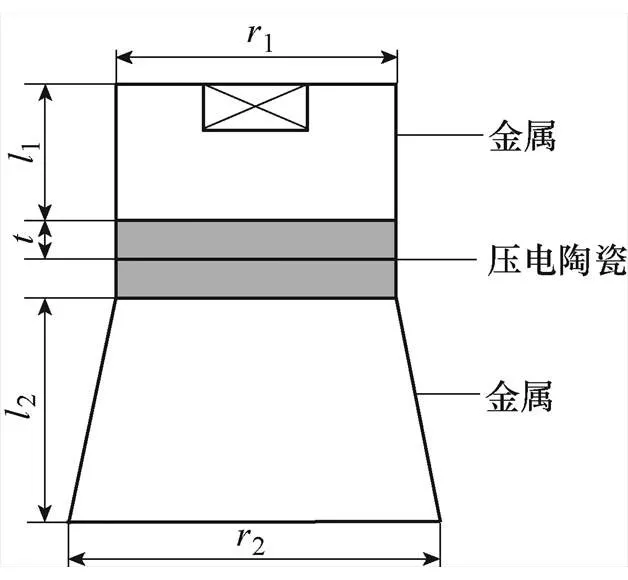
圖1 Langevin夾心式定子結構示意圖

動速度。d為壓電陶瓷環的靜態電容，其表達式為

<

圖2 傳統厚度振動模態壓電陶瓷機電等效電路模型

Fig.2 Conventional equivalent circuit of piezoelectrics in thickness vibration mode

為機電耦合系數，其表達式為

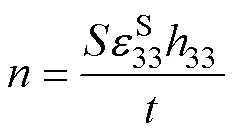
波速表示為

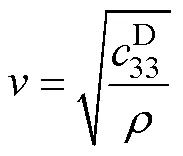
1p、2p和3p分別為機械分支中的阻抗，其表達式為

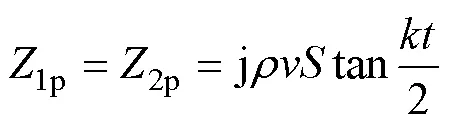
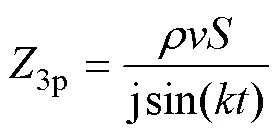
1.1 壓電振子結構含損耗機電等效電路模型

為深入研究超聲波電機定子內部的發熱機制，需要全面研究壓電振子的損耗特性。壓電振子含三類損耗：介電損耗、機械損耗和壓電損耗，分別用復數表示為

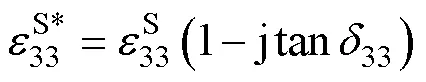
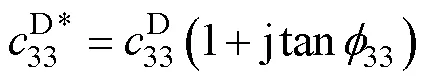
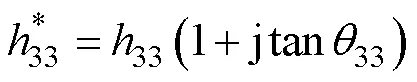
當考慮損耗時，對于機電等效電路中電學分支中的式（1）可用復數形式表示為

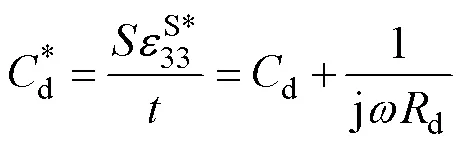
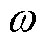
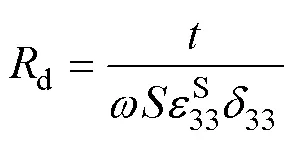
同樣地，等效電路電學分支中的式（2）可用復數形式表示為

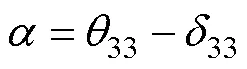
針對機電等效電路中機械側的參數，在考慮損耗情況下的式（4）和式（5）復數表示為

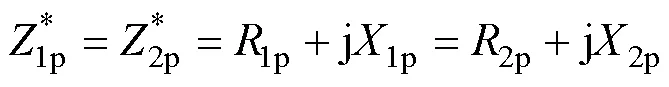
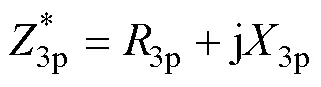
式中，1p、2p和3p為機械損耗；1p、2p和3p為存儲的機械能量，具體表達式為

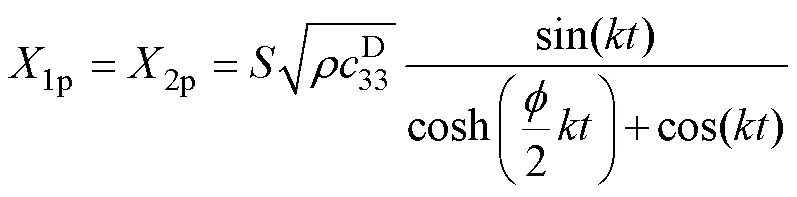
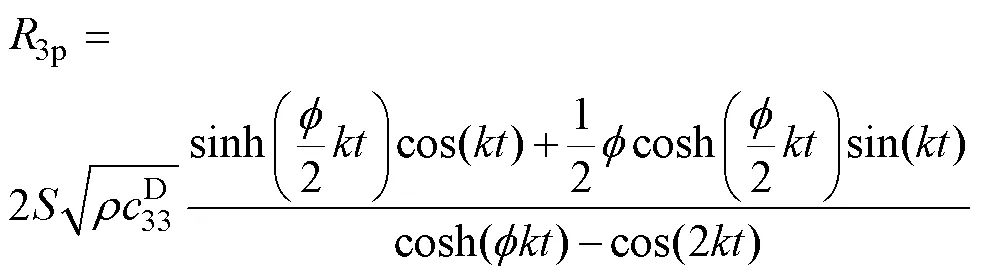
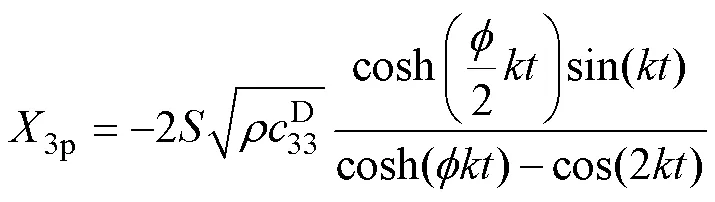
需要注意的是，1p2p具有電感特性，即代表機械系統中的質量；3p對應動態電容，即代表機械系統中的彈性。根據以上推導，新型含三類損耗的解耦機電等效電路模型如圖3所示。

圖3 新型含三類損耗的解耦機電等效電路模型

Fig.3 New decoupled electromechanical equivalent circuit with three types of losses

1.2 Langevin夾心式定子結構機電等效電路模型

由于Langevin結構中的兩側金屬僅具有機械特性，不具備電學特性，因此僅考慮金屬的機械損耗因子，其復楊氏模量可以表示為

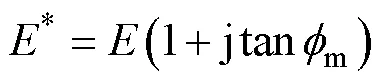
Langevin夾心式定子結構的等效電路機電模型如圖4所示，其中金屬結構的機械側參數表達式為

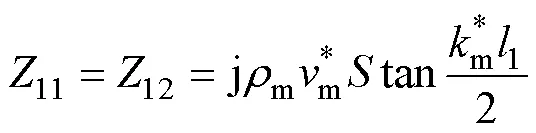
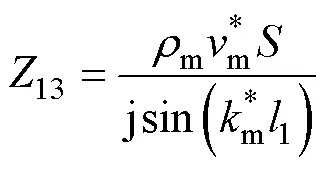
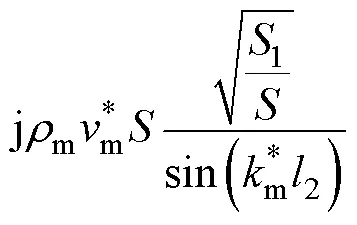
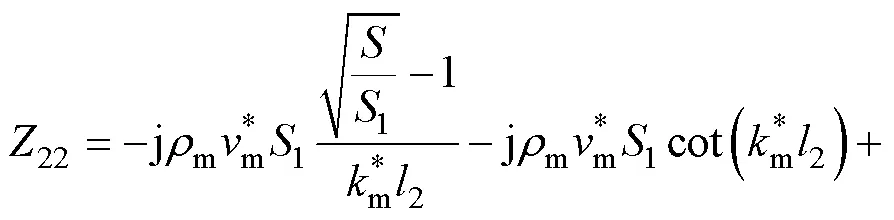
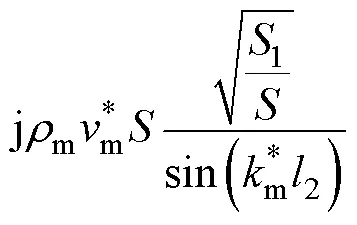
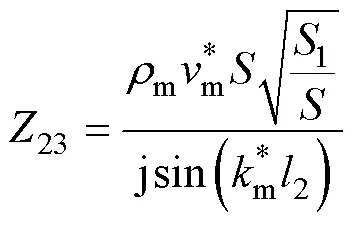
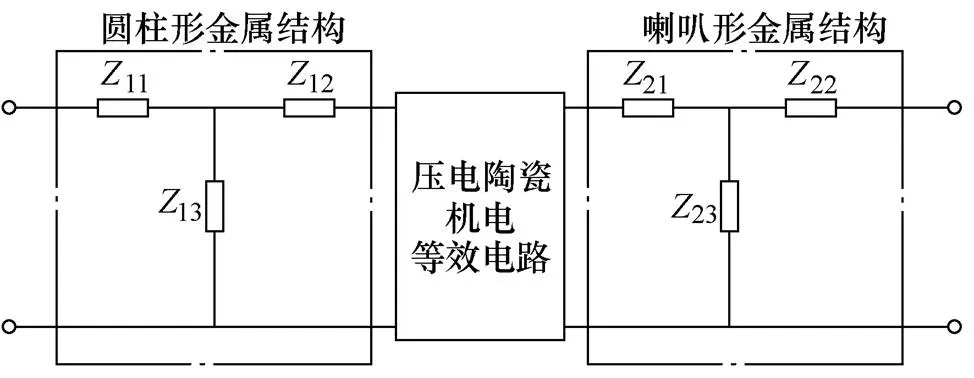
圖4 Langevin夾心式定子結構機電等效電路模型

2 仿真與實驗分析

2.1 壓電振子結構的仿真與實驗分析

本文采用的厚度振動模態下壓電振子的尺寸為：半徑1為18.5mm，單片厚度為5mm，其材料特性參數見表1。

表1 壓電振子的材料特性參數

利用仿真軟件Matlab（版本：R2022a）對圖3所示的壓電振子機電等效電路模型進行仿真分析。圖5為壓電振子阻抗頻率特性仿真結果對比，其中圖5a為不含損耗與含三種損耗的阻抗頻譜對比，可以看出兩種情況下的共振頻率和反共振頻率相同，即固有損耗不影響壓電振子的頻率特性，而兩者區別之處在于：不含損耗情況下，共振和反共振頻率處均出現尖峰，因此無法計算相對應的機械品質因數；圖5b為不含壓電損耗與含三種損耗仿真結果對比，兩者的區別在于共振頻率處的3dB帶寬不同，即對應的機械品質因數存在差異。在含損耗的情況下，可采用如圖6所示的3dB帶寬法計算共振頻率R處的機械品質因數R和反共振頻率A處的機械品質因數A，其表達式分別為

圖5 壓電振子阻抗頻率特性仿真結果對比

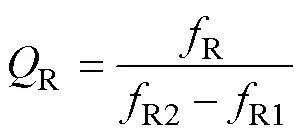
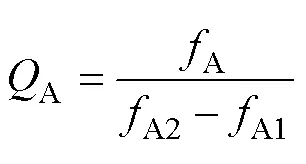
為了驗證仿真結果的準確性，利用高精度阻抗特性分析儀（E4990A, Keysight Technologies, Inc., Santa Rosa, CA）對壓電振子進行阻頻特性實驗測試，并將實驗結果與仿真分析進行比較，具體結果見表2。通過對比結果可以看出，相比于不含壓電損耗的仿真結果，含三類損耗的仿真結果與實驗結果更為接近，其準確度的提升尤其體現在表2中加粗顯示的數據，可以得出結論：壓電損耗對于共振條件下的機械品質因數影響較大。

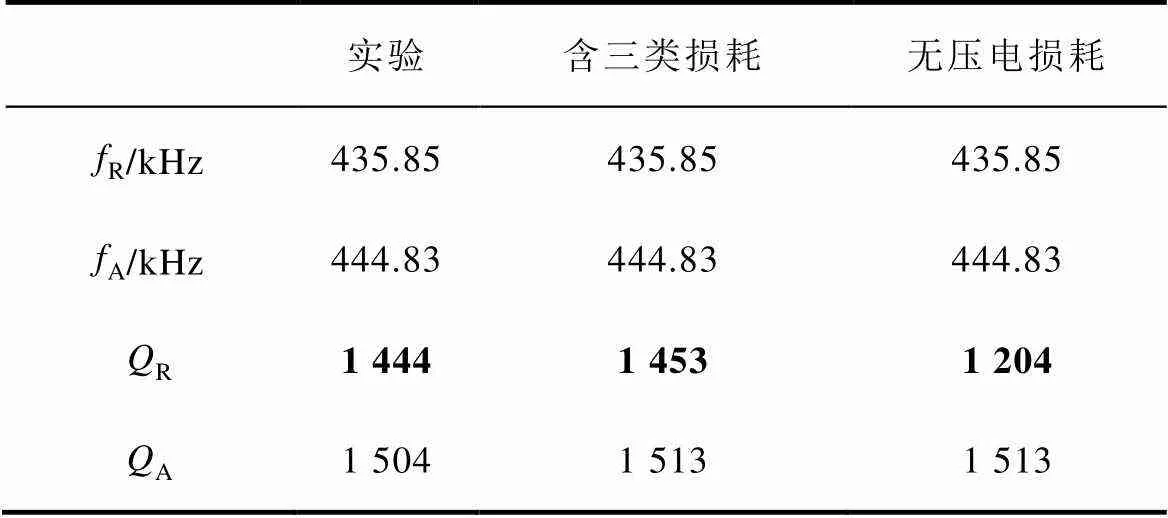
表2 含三類損耗、無壓電損耗的仿真與實驗結果對比

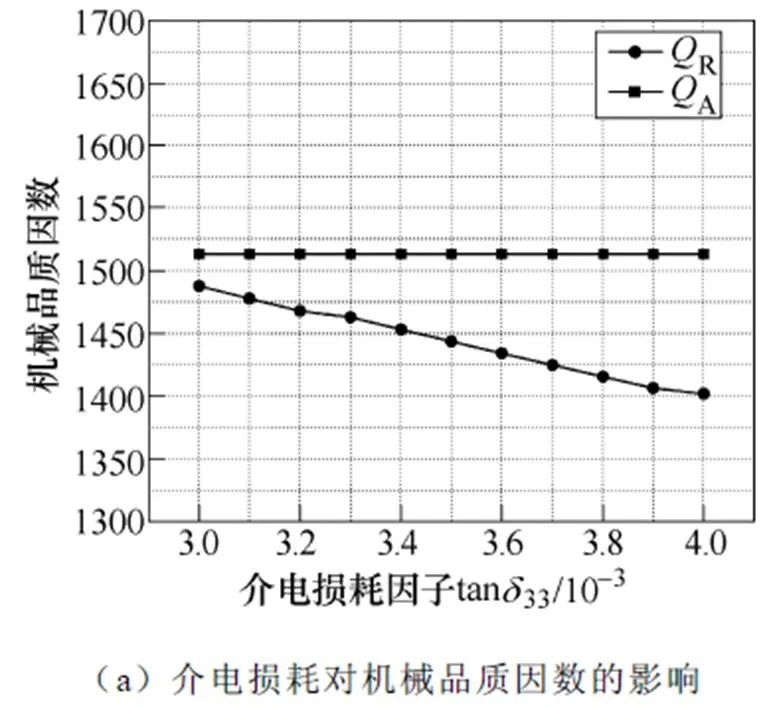
圖7所示為三類損耗特性對機械品質因數的影響規律，其中隨著介電損耗因子和機械損耗因子增加，共振頻率處的機械品質因數R呈現下降趨勢，而當壓電損耗因子增加時，R呈現升高趨勢；反共振頻率處的機械品質因數A則會隨著機械損耗因子的增加而減少，但不受介電損耗因子和壓電損耗因子的影響。

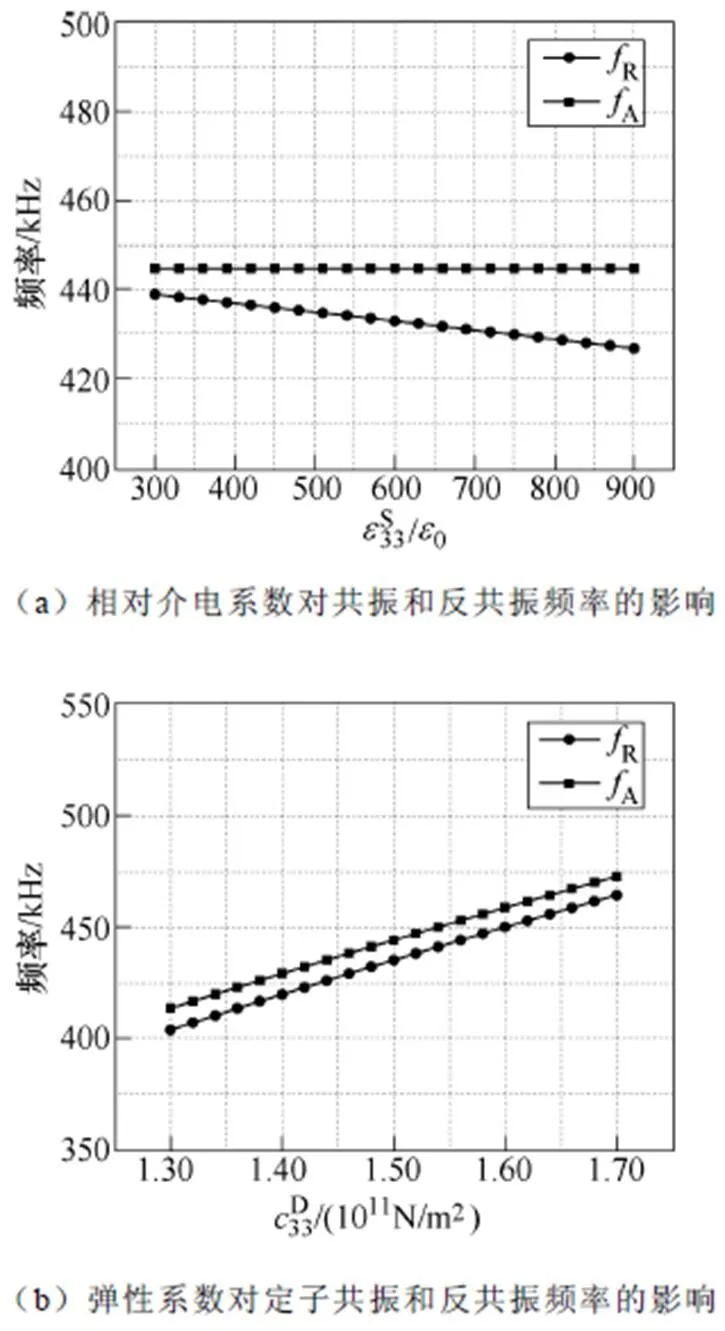
三類材料特性對壓電振子的共振頻率和反共振頻率的影響規律如圖8所示，其中共振頻率R隨著相對介電系數和壓電系數的增加而降低，但隨著彈性系數的增加而升高；反共振頻率A則會隨著彈性系數的增加而升高，但不受相對介電系數和壓電系數的影響。

有效機電耦合系數是描述電機定子機電轉換效率的重要參數，可以通過如下公式求得。

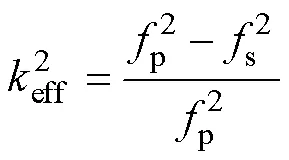
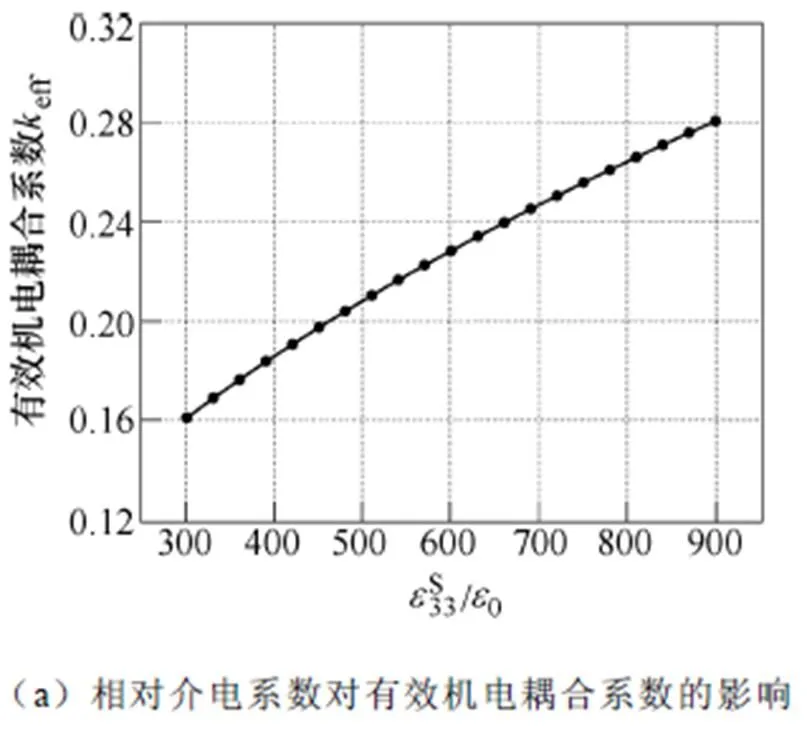
式中，s和p分別為壓電振子的串聯共振頻率和并聯共振頻率，可分別近似于共振頻率R和反共振頻率A。圖9為三類材料特性對有效機電耦合系數eff的影響規律，其中eff隨著彈性系數的增大而呈現下降趨勢，但隨著相對介電系數和壓電系數的增大而升高。

2.2 Langevin夾心式定子結構的仿真與實驗分析

Langevin夾心式定子結構中金屬的結構尺寸為：左側圓柱體金屬的厚度1=28mm，右側喇叭形金屬的厚度2=46mm，半徑2=29mm，材料特性為：楊氏模量=6.92×1010N/m2，密度為2 700kg/m3。基于上述參數，對如圖4所示的機電等效電路模型進行仿真，得到Langevin夾心式定子結構的共振頻率為28.392kHz。

為了驗證仿真模型結論，對Langevin夾心式定子結構采用激光測振儀（PolyTec PSV-400）進行測試。實驗測試平臺如圖10a所示，測試時，定子結構為自由狀態，將PSV-400各硬件連接成整套測試系統后，采用激光測振儀內部信號發生器產生正弦激勵信號，再通過功率放大器（NF 4052）將電壓信號進行放大，驅動信號通過數字示波器（Tektronix TDS 2014B）進行監控。激光測振過程采用系統自帶的軟件PSV8.51，依次按照如下步驟進行測試：光學設置→設置掃描點→設置參數→單點測試→掃描測量→顯示數據。測試時的原始測試界面如圖10b所示，由于掃描點設置和溫漂現象會對頻率產生一定影響，因此取5次測試結果平均值作為最終實驗值，測得的共振頻率為28.316kHz（最大偏差值為±0.035kHz）。考慮到建模中進行結構等效，忽略軸、螺栓和黏膠等結構引入的少量誤差，可認為仿真與實驗結果基本一致。

進一步地，可以根據機電等效電路模型對Langevin夾心式定子材料和結構特性進行分析。圖11為金屬的楊氏模量對共振和反共振頻率的影響規律，隨著楊氏模量的增加，共振頻率和反共振頻率同時增大。圖12為結構參數的變化對共振頻率和反共振頻率的影響規律，圖中，為圓柱體金屬的長度1與Langevin結構總長度的比值，隨著的增加，共振和反共振頻率呈現小幅度上升趨勢。相比于楊氏模量，結構參數對于頻率的影響較小。圖13和圖14分別表示金屬的楊氏模量和對有效機電耦合系數的影響規律。如圖13和圖14所示，隨著楊氏模量和結構參數的增加，有效機電耦合系數均呈現明顯的上升趨勢。該結論有助于通過合適地選取材料和設計結構來提升Langevin夾心式定子結構的機電能量轉換效率。

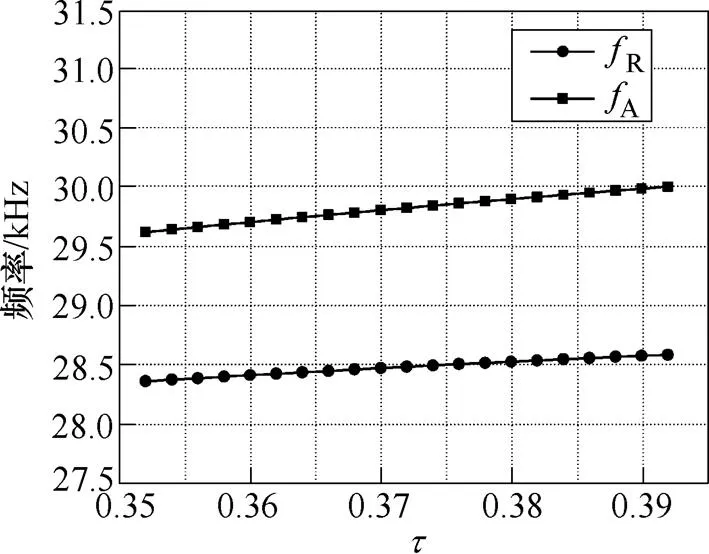
圖12 t 對共振和反共振頻率的影響仿真結果

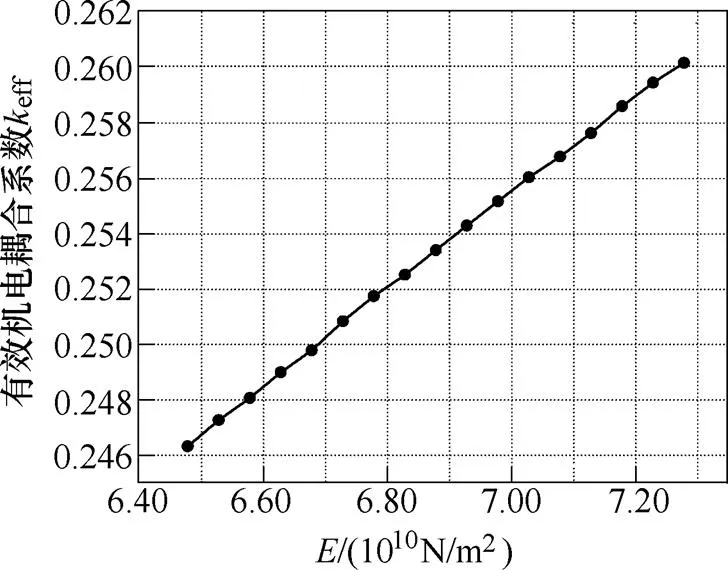
圖13 楊氏模量對有效機電耦合系數的影響仿真結果

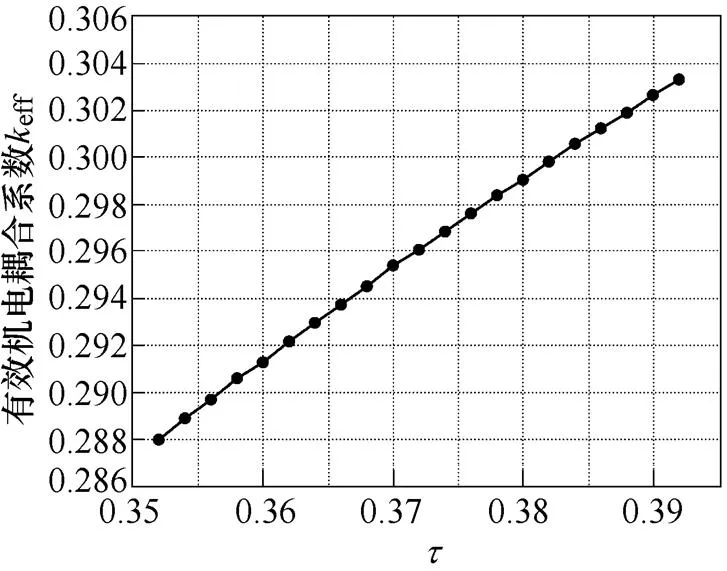
圖14 t 對有效機電耦合系數的影響仿真結果

3 結論

本文建立了含損耗的Langevin夾心式定子結構解耦機電等效電路模型，通過理論模型的仿真分析可得出以下結論：

1）壓電損耗對于厚度振動模態下壓電振子共振頻率處的機械品質因數影響較大。

2）共振頻率處的機械品質因數由三類損耗共同決定，而反共振頻率處的機械品質因數僅與機械損耗相關。

3）三類材料特性均對共振頻率產生影響，而反共振頻率僅受彈性系數影響較大。

4）材料和結構參數均對有效機電耦合系數產生較大影響。

綜上所述，通過所提出的模型可為進一步設計和優化Langevin夾心式定子結構提供理論支撐。

[1] Liu Yingxiang, Yan Jipeng, Wang Liang, et al. A two- DOF ultrasonic motor using a longitudinal-bending hybrid sandwich transducer[J]. IEEE Transactions on Industrial Electronics, 2019, 66(4): 3041-3050.

[2] Jiang Xinggang, Zhu Xianbin, Wong C Y, et al. Theory of series inductance matching to transducer at premechanical resonance zone in ultrasonic vibration cutting[J]. IEEE Transactions on Industrial Elec- tronics, 2019, 66(4): 3019-3029.

[3] Li Xuan, Stritch T, Manley K, et al. Limits and opportunities for miniaturizing ultrasonic surgical devices based on a Langevin transducer[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2021, 68(7): 2543-2553.

[4] 王天圣, 吳志軍, 馮平法, 等. 壓電超聲換能器電負載調頻特性研究[J]. 機械工程學報, 2017, 53(19): 45-51.

Wang Tiansheng, Wu Zhijun, Feng Pingfa, et al. Characteristics of piezoelectric ultrasonic transducer with electric load modifying frequency[J]. Journal of Mechanical Engineering, 2017, 53(19): 45-51.

[5] 劉繼倫, 劉素貞, 金亮, 等. 用于測厚和裂紋檢測的正交橫波電磁超聲換能器仿真分析及實驗研究[J]. 電工技術學報, 2022, 37(11): 2686-2697.

Liu Jilun, Liu Suzhen, Jin Liang, et al. Simulation and experiment of orthogonal shear waves with electro- magnetic acoustic transducer for thickness measure- ment and crack detection[J]. Transactions of China Electrotechnical Society, 2022, 37(11): 2686-2697.

[6] 姚睿豐, 王妍, 高景暉, 等. 壓電材料與器件在電氣工程領域的應用[J]. 電工技術學報, 2021, 36(7): 1324-1337.

Yao Ruifeng, Wang Yan, Gao Jinghui, et al. Applications of piezoelectric materials and devices in electric engineering[J]. Transactions of China Elec- trotechnical Society, 2021, 36(7): 1324-1337.

[7] 韋艷飛, 楊鑫, 陳鈺凱, 等. 計及損耗的超磁致伸縮材料參數提取及有限元仿真應用[J]. 電工技術學報, 2022, 37(7): 1726-1734.

Wei Yanfei, Yang Xin, Chen Yukai, et al. Parameter extraction and FEM simulation of giant mag- netostrictive transducer considering losses[J]. Transa- ctions of China Electrotechnical Society, 2022, 37(7): 1726-1734.

[8] 王光慶, 徐文潭, 楊斌強. T型直線超聲波電動機的運行機理及其特性分析[J]. 電工技術學報, 2017, 32(15): 111-119.

Wang Guangqing, Xu Wentan, Yang Binqiang. Operating mechanism and characteristics analysis of a T-shaped linear ultrasonic motor[J]. Transactions of China Electrotechnical Society, 2017, 32(15): 111- 119.

[9] 蔣春容, 董曉霄, 張津楊, 等. 徑向換能型超聲波電機定子振動模型[J]. 電工技術學報, 2017, 32(9): 48-55.

Jiang Chunrong, Dong Xiaoxiao, Zhang Jinyang, et al. Stator vibration model of a radial energy conversion ultrasonic motor[J]. Transactions of China Electro- technical Society, 2017, 32(9): 48-55.

[10] 王鑫, 王亮, 于鵬鵬, 等. 貼片式縱彎復合型直線超聲電機的理論建模與實驗研究[J]. 中國電機工程學報, 2021, 41(14): 5014-5024.

Wang Xin, Wang Liang, Yu Pengpeng, et al. Theoretical modeling and experiment studies of a bonded type longitudinal-bending hybrid linear ultrasonic motor[J]. Proceedings of the CSEE, 2021, 41(14): 5014-5024.

[11] Deng Yunyun, Zhang Guangbin, Zhang Xiaofeng. A method to depress the transmitting voltage response fluctuation of a double excitation piezoelectric transducer[J]. Applied Acoustics, 2020, 158: 107066.

[12] 陳誠, 林書玉. 基于2-2型壓電復合材料的新型寬頻帶徑向振動超聲換能器[J]. 物理學報, 2021, 70(1): 341-351.

Chen Cheng, Lin Shuyu. A new broadband radial vibration ultrasonic transducer based on 2-2 pie- zoelectric composite material[J]. Acta Physica Sinica, 2021, 70(1): 341-351.

[13] Li Xiaoniu, Yao Zhiyuan, Li Rong, et al. Dynamics modeling and control of a V-shaped ultrasonic motor with two Langevin-type transducers[J]. Smart Materials and Structures, 2020, 29(2): 025018.

[14] Wu Jiang, Mizuno Y, Nakamura K. Vibration characteristics of polymer-based Langevin trans- ducers[J]. Smart Materials and Structures, 2018, 27(9): 095013.

[15] Dal Bo L, Gardonio P, Turco E. Analysis and scaling study of vibration energy harvesting with reactive electromagnetic and piezoelectric transducers[J]. Journal of Sound and Vibration, 2020, 484: 115510.

[16] Dong Xiaoxiao, Jiang Chunrong, Jin Long, et al. Inherent loss analysis of piezoelectrics in radial vibration and its application in ultrasonic motor[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2020, 67(8): 1632-1640.

[17] American National Standards Institute. An American National Standard: IEEE Standard on Piezoelectricity Standard[S]. IEEE, 1988.

Electromechanical Equivalent Model of Sandwich Stator of Ultrasonic Motors Considering Losses

（College of Energy and Electrical Engineering Hohai University Nanjing 211100 China）

The Langevin sandwich structure is widely used in the stator design of ultrasonic motors, in which the piezoelectric vibrator works in the thickness vibration mode. Because the existing equivalent circuit model does not fully consider the inherent loss characteristics of the piezoelectric vibrator, it is unable to evaluate the mechanical quality factor. In this paper, the decoupling electromechanical equivalent circuit model of a piezoelectric vibrator with three types of losses is firstly established to study the influence of three types of inherent losses of piezoelectric ceramics on the mechanical quality factor. Then, the electromechanical equivalent circuit model of the Langevin sandwich structure is established, and the influence of material and structural parameters on resonance frequency, anti-resonance frequency and electromechanical coupling coefficient is discussed. Finally, a Langevin structural prototype is fabricated, and its impedance-frequency characteristics and vibration characteristics are tested. The accuracy of the theoretical model is verified. This paper provides theoretical support for designing a vibrator structure with a high mechanical quality factor and further develops a high-performance ultrasonic motor by revealing the differential influence of the inherent loss of piezoelectric vibrators on its output characteristics.

Ultrasonic motor, Langevin structure, electromechanical equivalent circuit, losses

TM35

10.19595/j.cnki.1000-6753.tces.220994

國家自然科學基金資助項目（52107043）。

2022-05-13

2022-07-09

董曉霄 女，1990年生，博士，副教授，碩士生導師，研究方向為微型特種電機設計及驅動控制、壓電發電技術和電動汽車相關 領域。

E-mail: dongxiaoxiao@hhu.edu.cn（通信作者）

黃肖肖 女，2000年生，碩士研究生，研究方向為微型特種電機設計及驅動控制。

E-mail: hhhuangxx@163.com

（編輯 郭麗軍）