一類帶有p-Laplacian算子的分數階微分方程邊值問題的多重正解①
胡芳芳, 劉元彬, 張永
1.伊犁師范大學 數學與統計學院,新疆 伊寧 835000;2.伊犁師范大學 應用數學研究所,新疆 伊寧 835000;3.新疆工程學院 數理學院,新疆 昌吉 830091
帶p-Laplacian算子的微分方程主要來源于非牛頓流體理論和多孔介質氣體的湍流理論.學者從多孔介質方程[1]中抽象出p-Laplacian方程,隨后此類方程被廣泛地應用到諸多領域,且p-Laplacian算子在許多物理工程的實際應用中可以更加具體地解釋一些復雜的物理現象,所以,越來越多的學者研究帶有p-Laplacian算子的分數階微分方程解的存在性[2-6].
隨著科學技術的進步和學者的深入研究,分數階微分方程模型引起了數學學者們的廣泛關注,在過去的幾十年里,分數階微分方程的成果豐碩[7-10],如:不同邊值條件下的正解性,其主要研究方法包括錐上不動點定理、上下解方法、單調迭代方法等[11-13].
文獻[14]利用Banach壓縮映射原理和Guo-Krasnosel’skii不動點定理得到了以下具有p-Laplacian算子的邊值問題
(1)
文獻[15]利用Guo-Krasnosel’skii不動點定理和上下解方法得到了具有p-laplacian算子的Caputo分數階微分方程邊值問題
(2)
的正解存在性的一些新結果.其中
2<α≤3φp(s)=|s|p-2sp>1
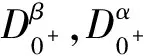
文獻[16]運用單調迭代法得到了分數階微分方程邊值問題
(3)
的正解的存在性結果.其中
α<0γ≤2β>0 1+β≤α
0<ξ,η<1φp(s)=|s|p-2sp>1
Dα,Dβ是標準的Riemann-Liouville型分數階導數.
基于上述研究,本文利用p-Laplacian算子考慮分數階微分方程邊值問題
(4)
1 預備知識

其中等式右端在[0,+∞)內有定義.

其中n是不小于α的最小整數.
引理1[18]設u(t)∈C[0,1]∩L1[0,1],且α>0,則
其中n是不小于α的最小整數.
引理2[18]設u(t)∈L1(0,1),且α>β>0,則
其中n是不小于α的最小整數.
引理3[18]設ρ>0,μ>0,則
引理4設y∈[0,1],1<β≤2,2<α≤3,則分數階微分方程邊值問題
(5)
有唯一解

(6)
其中
(7)
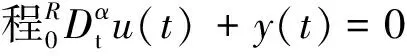
由邊值條件
u(0)=u′(0)=0
可得
c2=c3=0
(8)
因為α>β,對(8)式兩邊進行β階微分,可得
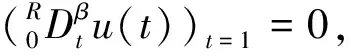
即
其中
引理5設g∈[0,1],1<β≤2,2<α≤3,則分數階微分方程邊值問題
(9)
有唯一解
(10)
其中
(11)
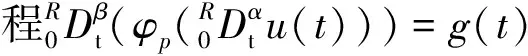
由邊值條件
可得
d2=0
即
即
由引理4可知
引理6函數G(t,s),H(t,s)滿足如下性質:
(i)對任意的t,s∈[0,1],G(t,s)≥0,H(t,s)≥0;
證(i)由函數G(t,s),H(t,s)的表達式可知(i)顯然成立.
(ii)若0≤s≤t≤1,則一定有
0≤t-s≤t-ts=t(1-s)
因此
(t-s)α-1≤tα-1(1-s)α-1
當0≤s≤t≤1時,有
當0≤t≤s≤1時,有
即
(iii)若0≤s≤t≤1,則一定有
0≤t-s≤t-ts=t(1-s)
因此
(t-s)β-1≤tβ-1(1-s)β-1
當0≤s≤t≤1時,有
當0≤t≤s≤1時,有
即
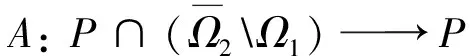
(i)‖Ax‖≤‖x‖(x∈P∩?Ω1),‖Ax‖≥‖x‖(x∈P∩?Ω2);
(ii)‖Ax‖≥‖x‖(x∈P∩?Ω1),‖Ax‖≤‖x‖(x∈P∩?Ω2).
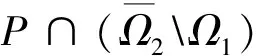
引理8[20]設P為實Banach空間E中的一個錐,
Pc={x∈P:‖x‖ P(θ,b,d)={x∈P:θ(x)≥b,‖x‖≤d} (i){x∈P(θ,b,d):θ(x)>b}≠?,且對x∈P(θ,b,d)有θ(Ax)>b; (ii)當‖x‖≤a時,‖Ax‖≤a; (iii)當x∈P(θ,b,c)且‖Ax‖>d時,θ(Ax)>b. 那么A至少有3個不動點x1,x2,x3,滿足 ‖x1‖ 記E=C[0,1],在E中定義范數 則E為Banach空間.定義錐P?E為 P={u∈E:u(t)≥0} 定義錐P上的非負連續泛函θ為 證設Ω是P的任意有界集,即存在一個常數γ>0,使得?u∈Ω,都滿足‖u‖≤γ.由于f(t,u(t))是連續的,則對于t∈[0,1],存在m>0,使得 0≤f(t,u(t))≤m 令 所有T(Ω)是一致有界的. 由于G(t,s)在[0,1]×[0,1]上是一致連續的,因此G(t,s)是一致連續的.對任意的ε>0,存在δ>0,使得當t1,t2∈[0,1],t1 于是 定理2假設f(t,u(t))為C[0,1]×[0,+∞)上的連續函數,其中 若存在兩個正常數r2>r1>0,使得 (i)當(t,u(t))∈[0,1]×[0,r1]時,f(t,u(t))≥φp(Nr1); (ii)當(t,u(t))∈[0,1]×[0,r2]時,f(t,u(t))≤φp(Mr2). 則方程(4)至少有一個正解u,使得r1<‖u‖ 證令 Ω1={u∈P:‖u‖ 當u∈?Ω1時,有 0≤u(t)≤r1t∈[0,1] 由(i)和引理6得 從而 ‖Tu‖≥‖u‖u∈?Ω1 令 Ω2={u∈P:‖u‖ 當u∈?Ω2時,有 0≤u(t)≤r2t∈[0,1] 可從(ii)和引理6得 從而‖Tu‖≤‖u‖,u∈?Ω2. 總之,通過引理7可知,方程(4)至少有一個正解u,且滿足r1<‖u‖ 定理3假設f(t,u(t))為C[0,1]×[0,+∞)上的連續函數,若存在滿足0 (i)當(t,u(t))∈[0,1]×[0,a]時,f(t,u(t))≤φp(Ma); (ii)當(t,u(t))∈[0,1]×[b,c]時,f(t,u(t))≥φp(Nb); (iii)當(t,u(t))∈[0,1]×[0,c]時,f(t,u(t))≤φp(Mc). 則方程(4)至少有3個正解u1,u2,u3,且滿足 下面證明引理8的條件(i)也是滿足的.很明顯, {u∈P(θ,b,d):θ(u)>b}≠? 若u∈P(θ,b,d),對任意的0≤t≤1有b≤u(t)≤d,通過(ii)可得 即對任意的u∈P(θ,b,d),θ(Tu)>b.因此滿足引理8中的條件(i). 最后,我們證明引理8的條件(iii)也是滿足的.對任意的u∈P(θ,b,c),都有θ(Tu)>b.因此,引理8的條件(iii)也成立. 綜上所述,引理8的所有條件都滿足.根據引理8,可以得出方程(4)存在3個正解u1,u2和u3,滿足 例1考慮邊值問題 其中 經過計算得 M≈1.766N≈2.949 應用定理3,例1至少有3個正解u1,u2,u3,且滿足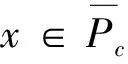
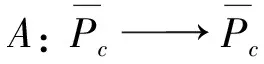
2 主要結論



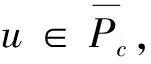
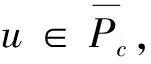
3 例子