半群的秩和3次方冪等元秩①
張心茹, 羅永貴, 劉木村
貴州師范大學 數學科學學院,貴陽 550025
設S是半群,A是S的非空子集且a,e∈S.若對任意的s∈S,存在a1,a2,…,am∈A,使得s=a1a2…am,則A是半群S的生成集,記S=〈A〉.若對半群S的任意生成集B都有|A|≤|B|,則A為半群S的極小生成集.通常半群S的秩定義為
rankS=min{|A|:A?S,〈A〉=S}
其中|A|為A的基數.
若e2=e,則e為半群S的冪等元,半群S中所有冪等元之集記為E(S).類似地,A中所有的冪等元之集記為E(A).
若(a3)2=a3且a3≠a,則a為半群S的3次方冪等元,所有3次方冪等元之集用E3(S)表示.類似地,A中所有3次方冪等元之集記為E3(A).
若A?E3(A),且對任意s∈S,存在b1,b2,…,bm∈A使得s=b1b2…bt,則A為半群S的3次方冪等元生成集.令M是半群S的任意3次方冪等元生成集且|A|≤|M|,則A為半群S的3次方冪等元極小生成集.進而|A|為半群S的3次方冪等元秩,記為
rank3(S)=min{|A|:A?E3(S),〈A〉=S}
設Xn={1,2,…,n}并賦予自然序,Tn和Sn分別是Xn上的全變換半群和對稱群,記Singn=TnSn,則Singn是Tn的子半群且Singn為奇異變換半群.記

ker(α)={(x,y)∈[n]×[n]:xα=yα}
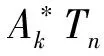
顯然
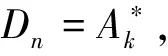
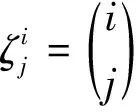
其中1≤i,j≤n且i≠j,即
設n≥3,3≤k≤n,記
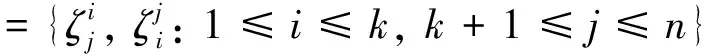
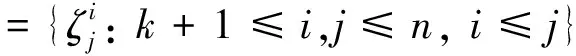
令E(Dn-1)為Dn-1中所有冪等元之集,于是有

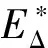
R(i,j)={α∈Dn-1:iα=jα}
Lq={α∈Dn-1:im(α)=Xn{q}}
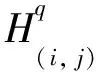
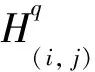

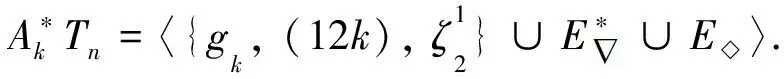
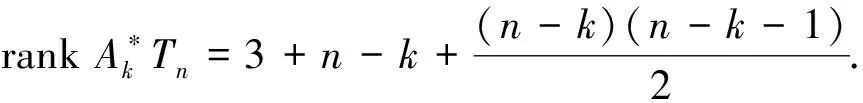
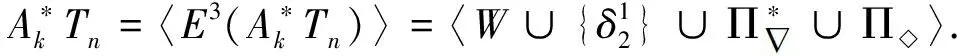
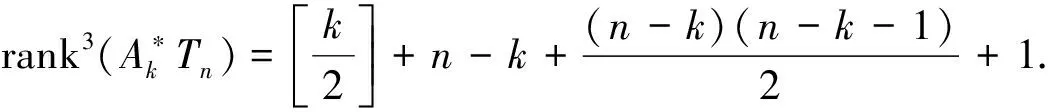
本文未定義的符號及術語參見文獻[12-16].
為完成定理1和定理2的證明,先給出以下若干引理:
引理1[2]當n≥3時,Singn=〈E(Dn-1)〉.


引理4[5]當1≤r≤n-2時,Dr?Dr+1·Dr+1.
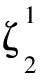
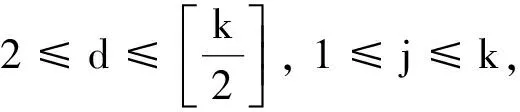

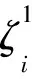
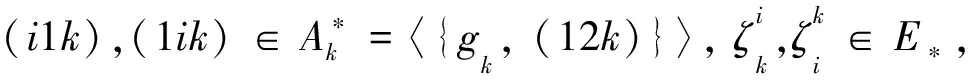
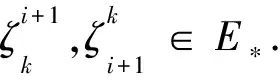
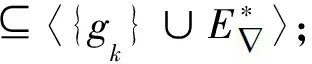
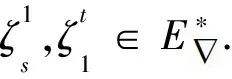
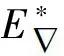
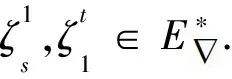
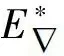

證易驗證,~是Dn-1上的等價關系.對任意α∈Dn-1,記
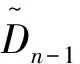
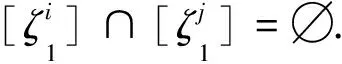
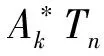
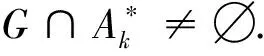
|im(αj)|≥n-1 |im(αp)|≥n-1 1≤j,p≤t
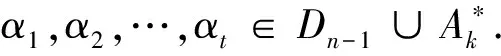
f=min{i:|im(αi)|=n-1,1≤i≤t}
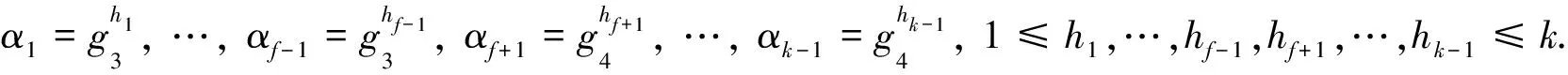
l=h1+…+hf-1p=hf+1+…+hk-1

|im(g1αfg2)|=|im(αf)|=n-1
設g1αfg2的唯一非單點核類為{x,y},則xg1αfg2=yg1αfg2.于是
xg1αfg2αk…αt=yg1αfg2αk…αt
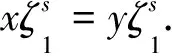
引理10設n≥3,3≤k≤n,則rankE*=3.
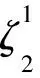
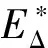
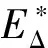
引理12設n≥3,3≤k≤n,當k為奇數時,rankE?=n-k+1;當k為偶數時,rankE?=n-k+2.

定理1的證明因為
再由引理1知Singn=〈E(Dn-1)〉.又因

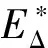
則
定理2的證明由定理1知
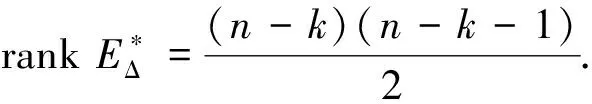
顯然
因此
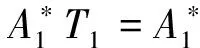
設δ∈Dn-1,且δ的唯一非單點核類為(i,j),其中i,j∈Xn,則Dn-1中3次方冪等元的形式如下:
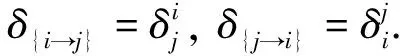
設n≥5,3≤k≤n.記
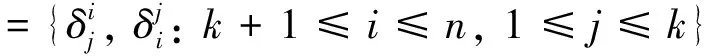
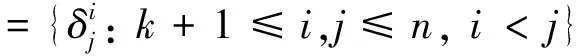
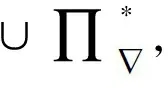
為完成定理3及定理4的證明,先給出以下若干引理:
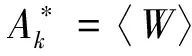

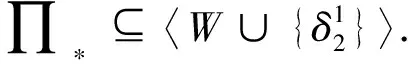
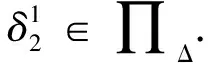
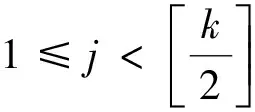

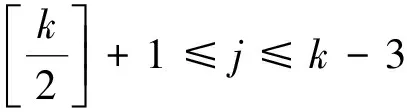
?
?


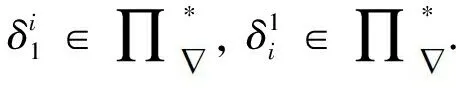
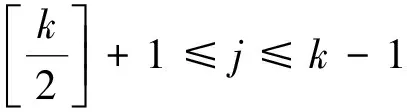
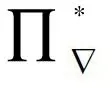
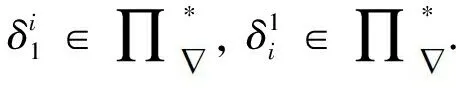
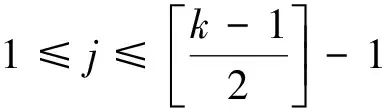

對任意的j∈{k-2,k-1,k},s∈{1,2,3},有
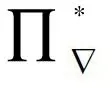
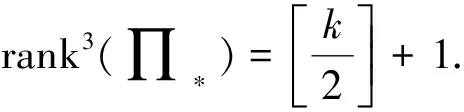
證根據引理13及引理14可知
從而

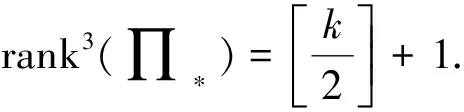
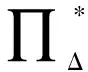
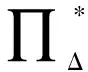
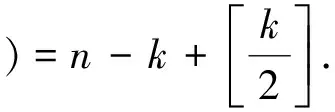

定理3的證明因為
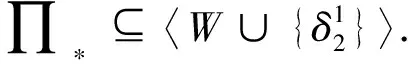
則
定理4的證明由定理3知
顯然
因此

