基于信號分析技術和人工智能算法的電力線路故障定位研究

董詩燾，路學剛，孫華利，葉清華

(1.云南電力調度控制中心，云南 昆明 650000； 2.南京南瑞繼保工程技術有限公司，江蘇 南京 211102)

行波分析理論經過不斷發展已經日趨成熟，被廣泛應用于輸電線路故障定位分析。比較常用的行波法有單端法和雙端法[1-4]。單端法是依據故障行波第一次到達一端母線量測點的時間以及故障點反射行波第1次到達同一端母線測量點的時間之差來進行故障定位。雙端法是根據故障點產生的沿線路向兩側傳播的故障行波波頭到達兩端母線量測點的時間之差進行定位[5-7]。由于對第1次反射波波頭的識別存在困難，因此單端法的分析精度較差。雙端法具有精度高的優點，但是需要GPS對時裝置和電力通信網絡基礎設施的支持，存在部署成本較高的問題[8-10]。行波法在實際應用中，遇到的另一個嚴重問題是串聯電容補償裝置主保護MOV的非線性，導致行波法不再適用于輸電線路的故障定位分析[11-13]。為此，本文提出基于信號分析技術和人工智能算法的電力線路故障定位分析方法。該方法僅需在變電站母線上部署一套故障電流量測設備和故障分析算法，無需復雜的GPS對時裝置和電力通信網絡基礎設施即可實現輸電線路故障的準確識別，具有部署成本低、精度高的優點。所提出的混合故障定位方法首先通過小波多分辨率分析方法檢測故障電流信號的瞬態發生時間，然后使用雙曲S變換對暫態故障電流信號進行時頻轉換處理以提取故障特征，隨后基于Parseval定理確定不同尺度上信號能量的分布以降低特征維度，最后使用BP-ANN根據選定的能量分布特征實現故障位置的識別。在電磁暫態程序/替代暫態程序(EMTP/ATP)中所模擬的電力線路系統中，對所提出的方法在不同條件下進行仿真測試，驗證了該方法的有效性、準確性和可靠性。

1 BP-ANN理論

包含輸入層、隱藏層和輸出層的BP-ANN模型如圖1所示。

圖1 BP神經網絡模型Fig.1 BP neural network model

圖1中的BP-ANN由3層組成：n個輸入節點、m個隱藏節點和i個輸出節點。輸入層到隱藏層的權值矩陣V為：V=(v1，v2，…，vm)，其中任意列向量vj是第j個隱藏節點對應的權重系數向量。隱藏層到輸出層的權值矩陣W為：W=(w1，w2，…，wi)，其中任意列向量wk是第k個輸出節點對應的權重系數向量。

BP-ANN訓練算法采用最速下降法計算網絡總誤差函數最小值，即沿著誤差函數的負梯度方向修正權系數。具體訓練過程包括輸入信號的正向傳播和輸出誤差信號的反向傳播2個過程[14-15]。

(1)輸入正向傳播。輸入信號沿輸入層經隱藏層，最終傳至輸出層。在信號傳輸過程中，上一層節點只影響下一層節點。輸出層節點比較當前輸出和期望輸出，如當前輸出不符合期望輸出，則輸出誤差信號，轉入反向傳播過程。

(2)誤差反向傳播。在反向傳播時，誤差信號按正向傳播的通道反向傳回，并在傳播過程中對每個隱藏節點的權重系數進行修改，以最小化誤差信號。每個節點的權重系數的改變量由傳播到該節點的誤差值所決定。

上述2個過程反復交替直至收斂。BP-ANN的訓練流程如圖2所示。

圖2 BP-ANN的訓練流程Fig.2 Training process of BP-ANN

BP-ANN傳輸函數選擇Sigmoid函數，訓練算法采用梯度下降法。設BP-ANN的輸入節點數為n，訓練樣本數為k，隱藏節點的輸出為hi(i=1，…，m)，輸出節點數為i。BP-ANN的輸入向量為X=[x1，x2，…，xn]T，輸出向量為O=[o1，o2，…，oi]T，則有：

(1)

式中，ωhi為輸出節點i的偏移量；ωji為隱藏節點j至輸出節點i的權重系數。

設輸出節點i的輸出為ti，則BP-ANN訓練的均方誤差函數為：

(2)

2 故障定位方法

高壓輸電線路故障定位系統的部署如圖3所示。

圖3中，從電流互感器 (CT) 的二次側測量輸電線路的三相電流。然后，通過本文所提的故障分析算法快速處理測量數據以識別故障位置，同時這些數據(包括測量數據和結果)通過局域網傳送到數據庫管理系統。作為故障事件的結果，所識別的故障信息被電網控制中心用于預測可能受影響的區域。

圖3 輸電線路故障定位系統的部署示意Fig.3 Deployment diagram of electric line fault location system

輸電線路故障位置識別算法如圖4所示。①利用小波多分辨率分析技術檢測故障的瞬時發生時間。②使用雙曲S變換對輸電線路暫態電流信號進行時頻轉換。③利用時頻域能量相等定理(Parseval定理)定量選擇能量分布。本文在2個周期內計算能量譜，一個周期是故障發生前的穩態信號，另一個周期是故障發生后的暫態信號。④訓練BP-ANN根據選擇的能量分布來識別故障位置。

圖4 故障位置識別流程Fig.4 Fault location identification process

3 仿真實驗與結果分析

3.1 實驗環境

在電子暫態程序/替代暫態程序(EMTP/ATP)中建立的仿真高壓輸電線路模型如圖5所示。圖5中有4條輸電線路、4個母線以及2個等效的三相電源(S1和S3)。母線BUS1和BUS2之間的傳輸線路(L1和L2)建模為雙回路耦合線。L3和L4建模為集中參數模型。每條傳輸線路總長45 km。負載2為通過升壓變壓器與BUS4連接的830 MVA 24 kV的同步電機。圖5中，SC為串補電容裝置，串補電容C=95.74 μF，串補度為40%。

圖5 高壓輸電線路仿真模型Fig.5 Simulation model of high voltage transmission line

圖5中，在L1F5、L2F5和L3F5三個位置分別設置單相接地故障(SLGF)、兩相接地故障(LLGF)、三相相間短路故障(LLLF)、三相接地故障(LLLGF)以及兩相相間短路故障(LLF)等不同類型的故障。

故障數據集來自圖5中輸電線路的母線SBUS和BUS3上的暫態電流波形測量值。數據集由0.3 s內采集的1 200個樣本組成，采樣頻率為4 kHz。實驗系統的額定頻率設定為50 Hz。

3.2 基于能量譜的HST實驗結果與分析

HST的頻率分解尺度在200～600，數據采樣的時間間隔為0.3 s，以4 kHz采樣頻率生成17個分解尺度。

當發生A相SLGF時，在SBUS和BUS3上分別測量的能量譜分布如圖6、圖7所示。發生LLLGF時，SBUS和BUS3上測量的能量譜分布如圖8、圖9所示。

圖6 不同位置發生SLAG故障時在SBUS上的能量譜Fig.6 Energy spectrum on SBUS when SLAG fault occurs at different locations

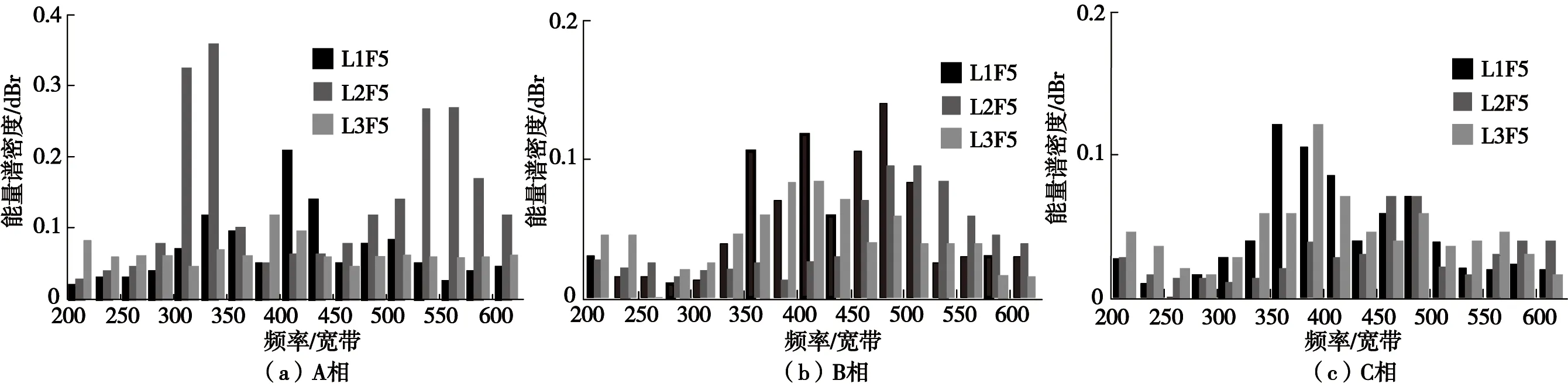
圖7 不同位置發生SLAG故障時在BUS3上的能量譜Fig.7 Energy spectrum on BUS3 when SLAG fault occurs at different locations

圖8 不同位置發生LLLGF故障時在SBUS上的能量譜Fig.8 Energy spectrum on SBUS when LLLGF fault occurs at different locations

圖9 不同位置發生LLLGF故障時在BUS3上的能量譜Fig.9 Energy spectrum on BUS3 when LLLGF fault occurs at different locations

由上述結果可知，同一故障類型同一位置的能量分布的輪廓相似，不同類型和不同位置的故障行波信號中高頻域能量會表現出明顯不同分布特征。

3.3 BP-ANN實驗結果與分析

選取3個不同故障位置和不同過渡電阻進行故障定位測試。對每個故障電流信號采樣777個數據樣本，其中過渡電阻分別為10、50、100 Ω。對于每個過渡電阻，電壓故障發生的時間間隔為1/(60×36) s，而總的過渡時間是0.1 s到0.116 66 s。

輸入數據集的大小為1 200×(L×3×777)。通過基于能量譜的HST(PS-HST)對完整輸入數據集進行處理，形成大小為17×(L×3×777)能量譜數據集，作為BP-ANN的輸入數據集。其中，L是故障位置的數量。為了檢驗BP-ANN的判別效果，輸入數據集被隨機地分為2個大小接近的訓練和測試樣本集。

向BP-ANN中輸入訓練樣本集后，開始訓練神經網絡。首先選擇隱藏層節點數為3，然后逐漸增加到12。得到BP-ANN的誤差曲線如圖10所示。確認隱含層節點數為9時誤差最小。

圖10 BP-ANN訓練曲線Fig.10 BP - ANN training curve

完成BP-ANN的訓練后，輸入測試樣本集，測試結果和誤差見表1。

表1 測試結果Tab.1 Test result

由表1可知，在不同故障類型、不同過渡電阻、不同故障距離的仿真條件下，本文提出的故障定位方法表現出了較高的定位精度，絕對誤差在250 m以內，相對誤差在1%以內，能夠滿足故障定位的精度要求。

4 結論

本文提出了一種基于信息分析技術和人工智能算法電力線路故障位置識別方法。該方法只需要在母線一側部署一套電流監測裝置和故障定位算法，即可實現電力線路故障位置的識別。在考慮到故障類型和過渡電阻2個因素的條件下，對所提出的故障定位方法的性能進行仿真測試，結果表明該故障定位方法的準確性和可靠性能夠滿足電力線路的故障定位要求。