波形鋼腹板-UHPC 組合連續箱梁橋靜力和抗震性能研究

朱平，丁子賢，張哲，邵旭東

［1.湖南大學土木工程學院，湖南長沙 410082；2.風工程與橋梁工程湖南省重點實驗室（湖南大學），湖南長沙 410082；3.湖南工業大學土木工程學院，湖南株洲 412007］

超高性能混凝土（Ultra-high Performance Con?crete，UHPC）是一種新型水泥基復合材料，采用顆粒組分優化級配的方式構建，具有非常高的堆積密度［1］，抗壓強度可達120～200 MPa［2］.不連續的孔隙結構能有效減少液體的進入，耐久性得到顯著提升［3］.摻入的鋼纖維在UHPC 基體內不連續且亂向分布，使UHPC 具有持續的開裂后拉伸性能，抗拉強度可超過8 MPa［4］.

目前，大跨徑預應力混凝土（Prestressed Con?crete，PC）連續梁橋存在自重過大，主跨過度下撓以及梁體開裂嚴重的難題.造成這些問題的主要原因在于普通混凝土（Normal Concrete，NC）抗拉強度低、徐變系數較大.邵旭東教授研發團隊［5］利用UHPC高強度、高耐久性的特征，提出了單向預應力UHPC 薄壁箱梁結構，并將這種新的結構形式應用于工程實踐：廣東省英德市已建成世界最大跨徑的單向預應力UHPC 簡支箱梁橋（跨徑102 m），該橋運營狀態良好，受到工程界的一致好評.

為克服普通混凝土箱梁橋腹板易開裂問題，法國提出由平鋼腹板（Flat Steel Web，FSW）代替混凝土腹板的概念.但FSW 沿縱向無法自由伸縮，使得FSWs-NC 組合橋梁預應力損失較嚴重.為此，法國Campenon Bernar公司提出一種可沿橋梁縱向自由伸縮的新型鋼腹板形式：波形鋼腹板（Corrugated Steel Web，CSW）［6］.波形鋼腹板不約束頂、底板的變形，幾乎全部預應力都可作用在頂板和底板上.法國將波形鋼腹板引入工程項目中，取得了良好的效果，并在全世界范圍推廣.法國、德國、日本等國相繼建成了Cognac橋、Dole橋、Altwipfergrund橋、日見夢大橋、安威川大橋等，橋型包括簡支梁、連續梁、連續剛構、斜拉橋等.我國也建成了江蘇淮安長征人行橋［7］、鄄城黃河公路大橋、深圳平鐵大橋等［8］.CSWs-NC 組合箱梁橋消除了普通混凝土腹板開裂的風險；對比PC箱梁橋，可降低結構自重約1/5～1/4；無腹板鋼筋綁扎立模的過程，施工更為簡單方便.

雖然CSW 可降低主梁的重量，但箱梁的頂板和底板采用NC 使得組合橋梁的自重仍然較大，并成為制約CSWs-NC 組合箱梁橋跨徑進一步增大的瓶頸.NC 具有較大的徐變，使得大跨預應力混凝土連續梁橋中跨跨中過度下撓的問題仍難以有效解決［9-10］.并且，NC 較低的抗拉強度使得頂、底板仍然易開裂；在使用階段，受壓區普通混凝土的正截面最大壓應力限值較低，例如16.2 MPa（C50混凝土）.

受已建成UHPC 橋梁自重輕、性能優異的啟發，本文嘗試將CSWs-NC 組合箱梁橋的頂、底板替換為UHPC 板，提出CSWs-UHPC 組合連續箱梁結構，以期能大幅減輕上部結構自重，提升CSWs-UHPC 組合連續箱梁橋的跨徑，改善主梁跨中過度下撓的問題，消除頂、底板開裂的風險.這種新型組合體系橋梁能突破CSWs-NC 組合箱梁橋的瓶頸，成為大跨徑連續梁橋中有較強競爭力的一種結構型式.

為驗證CSWs-UHPC 組合結構的可行性，本文設計了一座78 m+130 m+78 m 三跨CSWs-UHPC 組合連續箱梁橋，利用Midas/Civil 建立了整橋有限元模型，對其進行靜力分析［11］.在此基礎上，為便于CSWs-UHPC 組合連續箱梁橋結構設計，本文對該新型組合橋梁的合理中支點梁高、中跨跨中梁高進行了分析，提出組合梁合理的梁高范圍.然后，分析了CSWs-UHPC 組合箱梁橋的動力特性；研究了E2 地震波縱向激勵作用下，組合梁端位移、墩底彎矩和剪力以及高阻尼橡膠支座的滯回耗能特性，可為CSWs-UHPC組合箱梁橋的工程應用提供參考.

1 波形鋼腹板-UHPC組合箱梁橋方案設計

1.1 縱橫斷面設計

橋梁上部結構為三跨CSWs-UHPC 組合連續箱梁，跨徑布置為78 m+130 m+78 m，立面如圖1 所示.主橋分左右雙幅，單幅橋采用單箱單室截面，中跨跨中及邊跨支點梁高為3.5 m，中墩支點梁高為7.5 m.CSWs-UHPC 箱梁頂板寬10.0 m；UHPC 橋面板采用帶有縱肋的矮肋板，UHPC 矮肋板的面板厚8 cm，縱肋高14 cm，縱肋間距設為70 cm.UHPC 橋面板下沿縱向每隔2.4 m 設置一道1.1 m 高的UHPC 橫肋，橫肋厚度為12 cm，形成正交異性UHPC 矮肋板橋面體系，使組合箱梁頂板的主受力方向由橫橋向變為縱橋向.UHPC 橫肋可有效減小車輪荷載作用下橋面板的縱向應力［12-13］，并有利于體外預應力束的布置.箱梁節段示意圖如圖2 所示.UHPC 底板寬8.0 m，底板厚度沿縱向在20～45 cm之間變化；腹板采用Q345波形鋼腹板.采用節段預制懸臂拼裝法施工，相鄰節段頂、底板之間采用環氧樹脂膠進行接縫處理，相鄰CSW 的連接采用焊接.CSWs-UHPC 箱梁截面布置如圖3所示.

圖1 CSWs-UHPC組合連續梁橋立面布置圖（單位：cm）Fig.1 Elevation layout of corrugated steel webs-UHPC composite continuous box girder bridge（unit：cm）

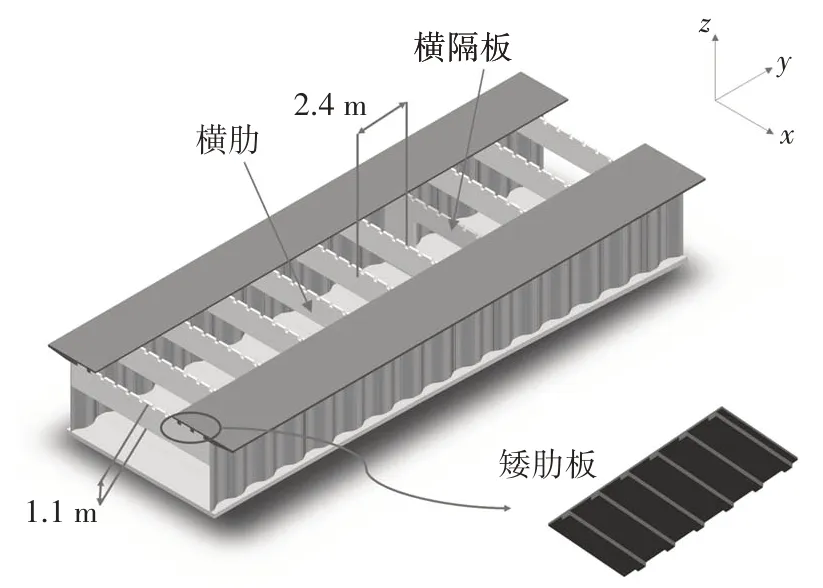
圖2 CSWs-UHPC組合箱梁節段Fig.2 Segmental schematic of corrugated steel webs-UHPC composite box-girder

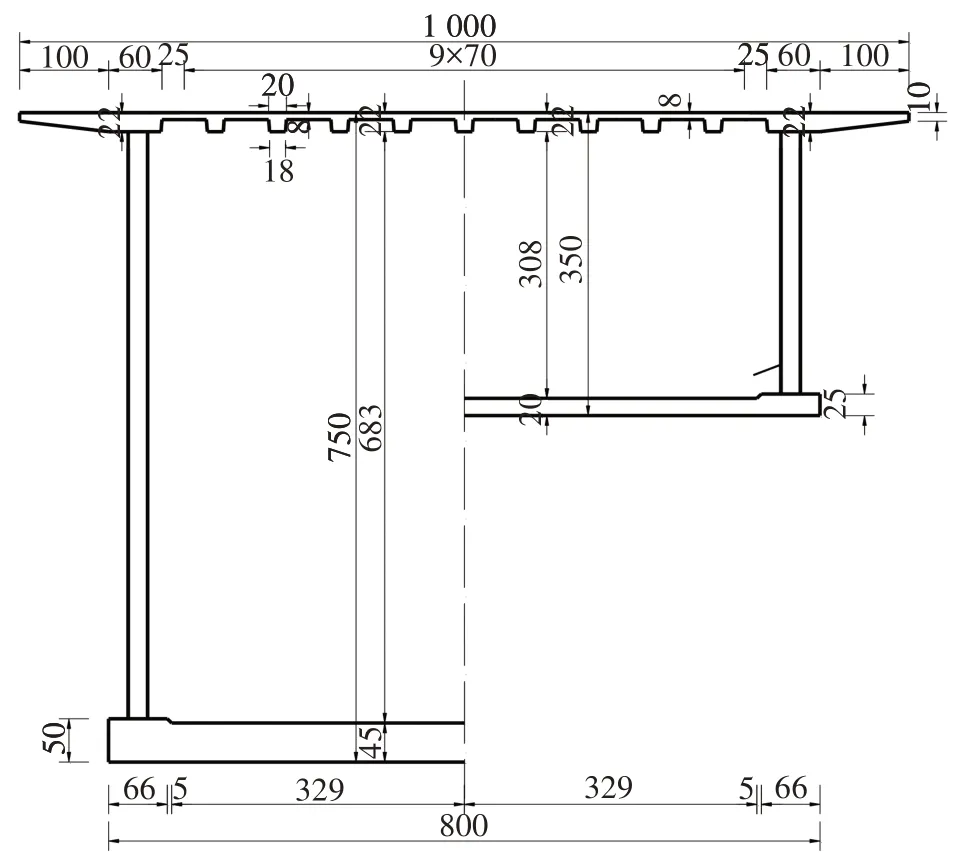
圖3 CSWs-UHPC箱梁截面（單位：cm）Fig.3 Typical cross section of corrugated steel webs-UHPC composite box-girder（unit：cm）

1.2 波形鋼腹板設計

本橋采用1600 型波形鋼腹板［14］，可在工廠采用模壓法加工成長6 400 mm 的安裝構件后，再運送至制梁場地進行CSWs-UHPC 組合箱梁預制節段的施工.要求CSW 整節段模壓成型，節段內無焊縫［15］.CSWs-UHPC 組合連續梁橋的CSW 厚度變化范圍為12～28 mm.

1.3 UHPC頂、底板與波形鋼腹板的連接

CSW 與UHPC 頂、底板的連接采用翼緣板+栓釘的連接方式.翼緣板厚18 mm，寬550 mm，栓釘直徑22 mm，高100 mm，橫向間距為200 mm，縱向間距為150 mm，一個翼緣板上可布置3列栓釘.UHPC 頂、底板連接件的布置形式相同.

1.4 UHPC橫隔板

在CSWs-UHPC 組合連續箱梁橋邊跨和中跨各設置4道和8道橫隔板，以提高主梁抵抗扭轉畸變的能力，橫隔板厚度為16 cm.部分橫隔板兼具體外預應力的轉向作用，該類橫隔板在靠近底板處為馬蹄形，厚50 cm.UHPC 橫隔板與波形鋼腹板之間采用栓釘連接.

1.5 單向預應力體系

CSWs-UHPC 組合箱梁結構中密集布置的UHPC 橫肋與矮肋式UHPC 頂板形成正交異性橋面體系［13］，頂板無須設置橫向預應力，僅沿橋梁縱向設置預應力，從而形成單向預應力CSWs-UHPC 組合連續箱梁體系.由于組合箱梁的UHPC 頂板和底板較薄，為合理布設預應力筋，采用全體外預應力形式［16］.體外預應力束采用Φs15.2 高強度低松弛環氧涂覆無黏結成品索［17］，懸臂體外頂板束位于頂板下方，靠近頂板處布置；合攏體外底板束位于底板上方，靠近底板處布置.

1.6 應用前景分析

按照橋梁跨徑、橋寬、跨中和支點梁高以及結構設計性能目標相同的原則，設計了CSWs-NC 組合連續箱梁橋和預應力混凝土連續箱梁橋，與本文提出的CSWs-UHPC 組合箱梁橋進行對比.3 種方案均采用節段預制懸臂拼裝法施工，CSWs-NC 組合箱梁橋和PC 連續箱梁橋的截面布置分別如圖4 和圖5所示.

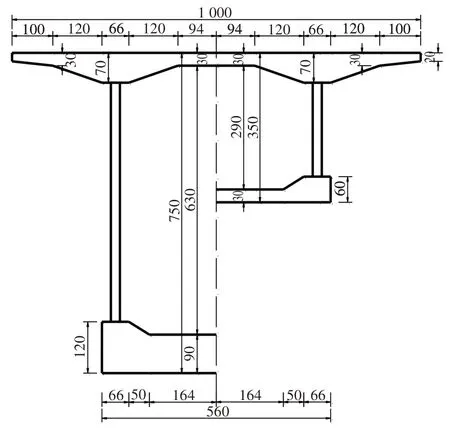
圖4 CSWs-NC組合箱梁橋截面布置圖（單位：cm）Fig.4 Typical cross section of CSWs-NC composite continuous box girder bridge（unit：cm）

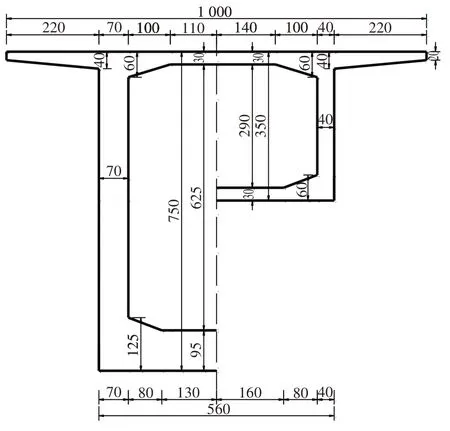
圖5 PC連續箱梁橋截面布置圖（單位：cm）Fig.5 Typical cross section of PC continuous box girder bridge（unit：cm）

1.6.1 上部結構自重及有效性分析

3 種方案的上部結構自重及自重效應對比如表1 所示.由表1 的數據可以看出，CSWs-NC 組合箱梁橋對比PC箱梁橋，上部結構自重降低了16.6%，中支點負彎矩減小了14.6%，活荷載效應比增加了15.0%，說明僅將混凝土腹板替換為波形鋼腹板對于降低中支點負彎矩和提高結構有效性的作用有限.相對于CSWs-NC 組合箱梁橋和PC 箱梁橋，CSWs-UHPC 組合箱梁橋上部結構自重分別降低了45%和54%，自重荷載作用下中支點負彎矩分別降低了45.8%和53.8%，活荷載效應比（活荷載效應與總效應之比）則分別增加了66.9%和91.8%.這表明使用CSWs-UHPC 組合箱梁這種結構型式能顯著降低自重，大大減小中支點處負彎矩，結構抵抗活荷載的有效性得到明顯增強，對提升連續梁橋主跨跨越能力具有較大潛力.

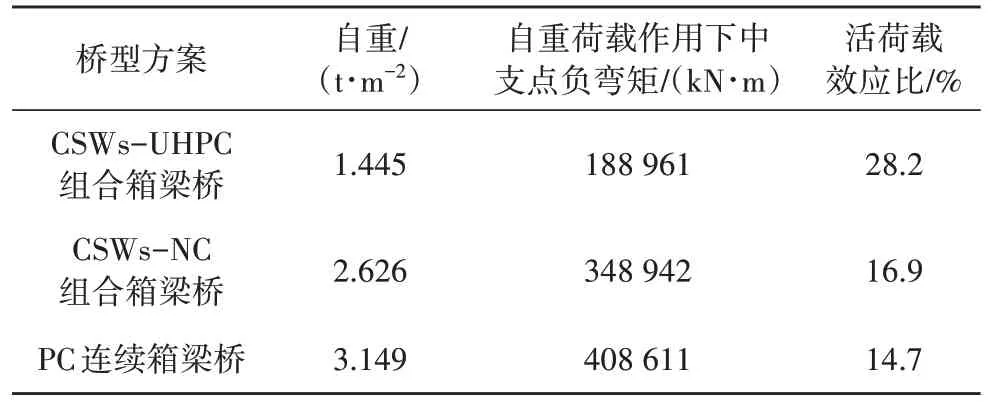
表1 結構自重及有效性對比Tab.1 Comparisons of dead weight and its effectiveness

1.6.2 耐久性和經濟性分析

PC 箱梁橋存在較為嚴重的耐久性病害，如梁體開裂、跨中過度下撓［9，18-19］、體內預應力管道壓漿不密實導致的預應力筋銹蝕等問題［17］.CSWs-UHPC 組合箱梁頂、底板采用UHPC 替換NC，使箱梁頂、底板基本無開裂風險；波形鋼腹板無開裂隱患，且橋梁鋼結構防腐技術也已經相當成熟；預制CSWs-UHPC組合箱梁結構在蒸汽養護后，UHPC 頂、底板的后期收縮可基本消除，并且徐變也遠小于NC，可有效解決傳統大跨梁橋跨中過度下撓的問題；CSWs-UHPC組合箱梁橋采用全體外預應力體系，體外預應力束采用無黏結鋼絞線外包HDPE 防護［17］，易檢測，可更換，耐久性優異.

將CSWs-UHPC 組合箱梁橋的經濟性與CSWs-NC 組合箱梁橋及PC 箱梁橋進行對比，如表2 所示.CSWs-UHPC 組合箱梁橋上部結構自重大幅降低，使得運輸吊裝費用降低，下部結構材料用量也可減少.經估算，對比CSWs-NC 組合箱梁橋和PC 連續箱梁橋，CSWs-UHPC 組合箱梁橋的綜合單價僅分別增加了16.8%和6.5%.但CSWs-UHPC 組合箱梁橋耐久性能優異，且能避免傳統大跨徑梁橋各種常見病害的產生，可大幅度降低橋梁病害所帶來的后期養護費用，綜合而言，CSWs-UHPC 組合箱梁結構在橋梁全壽命周期成本上仍具有競爭力.

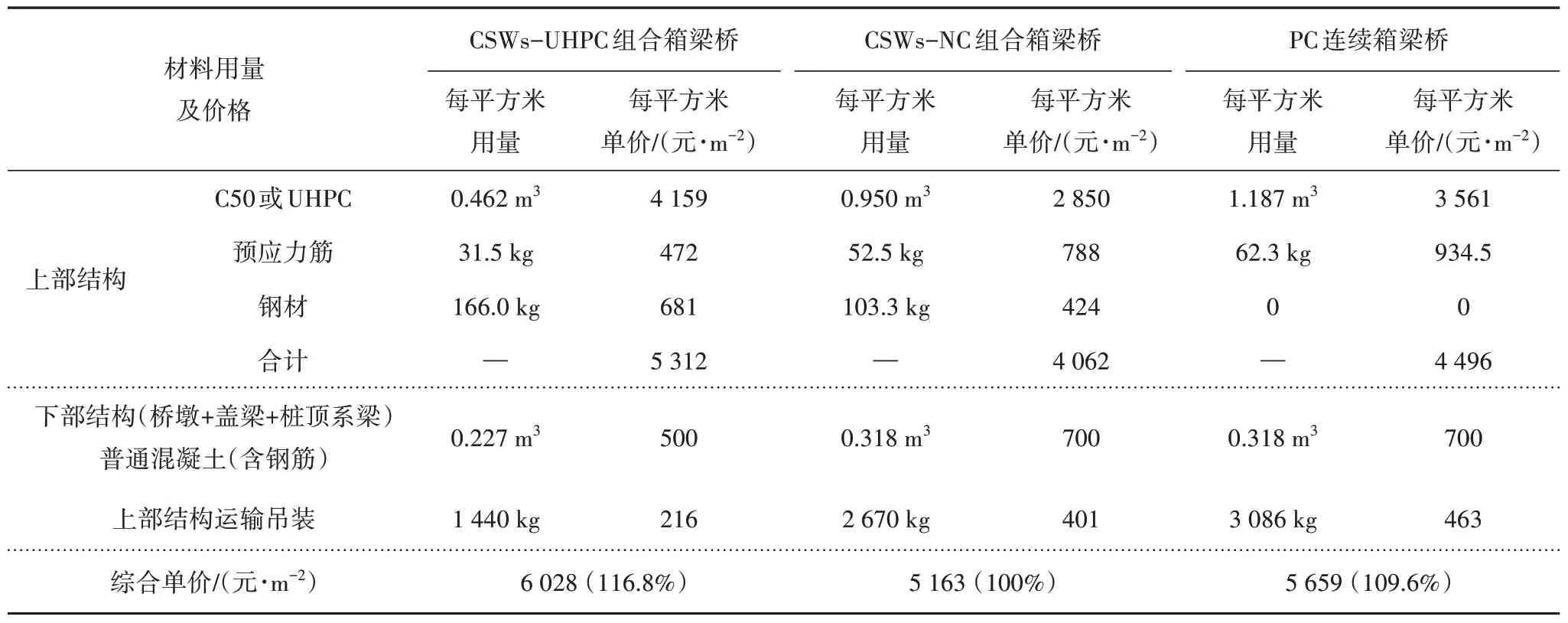
表2 方案經濟性比選表Tab.2 Economic performance among different bridge types

2 波形鋼腹板-UHPC 組合箱梁橋靜力性能分析

采用有限元軟件Midas/Civil 建立CSWs-UHPC組合連續箱梁橋的空間桿系模型，模型包含84 個梁單元.按照體外預應力鋼束的形狀并設定適當的摩擦系數，在模型上施加預應力荷載以模擬體外預應力鋼束的作用.模型的計算假定：1）波形鋼腹板與UHPC 頂和底板固結，并共同受力；2）UHPC 頂板和底板承擔縱向彎矩，波形鋼腹板承擔橫向剪力；3）組合梁彎曲時符合平截面假定.

有限元模型中相關參數取值為：1）UHPC 材料性能參考《超高性能混凝土梁式橋技術規程》（T/CCES 27—2021），UHPC 彈性模量取41.9 MPa，泊松比取0.2，抗壓、抗拉強度設計值分別取58 MPa、3.3 MPa，抗壓強度標準值取84 MPa［22］.CSW 和預應力筋的材料特性參考《波形鋼腹板組合梁橋技術標準》（CJJ/T 272—2017）［14］；2）一期恒載按橋梁設計自重取值，二期恒載為32.5 kN/m；考慮整體溫升和溫降20 ℃，梯度溫升、溫降按照《公路橋涵設計通用規范》（JTG D60—2015）取值［23］；汽車荷載等級為公路-Ⅰ級；支座沉降取值為：邊支座沉降5 mm，中支座沉降10 mm；經高溫蒸養后，UHPC 的徐變系數終極值取為0.2［22］.

2.1 承載能力極限狀態分析

CSWs-UHPC 組合連續箱梁的最小彎矩、最大彎矩設計值及彎矩抗力如圖6所示，由圖6可知主梁抗彎承載力計算滿足規范《超高性能混凝土梁式橋技術規程》（T/CCES 27—2021）要求［22］.

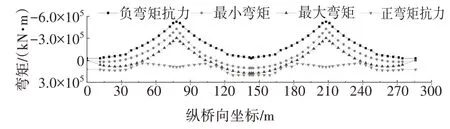
圖6 主梁彎矩包絡及抗力圖Fig.6 Bending moment envelope and flexural resistance of the main girder

主梁最大剪力、最小剪力及剪力抗力如圖7 所示，由圖7 可知主梁抗剪承載力計算滿足規范CJJ/T 272—2017要求［14］.

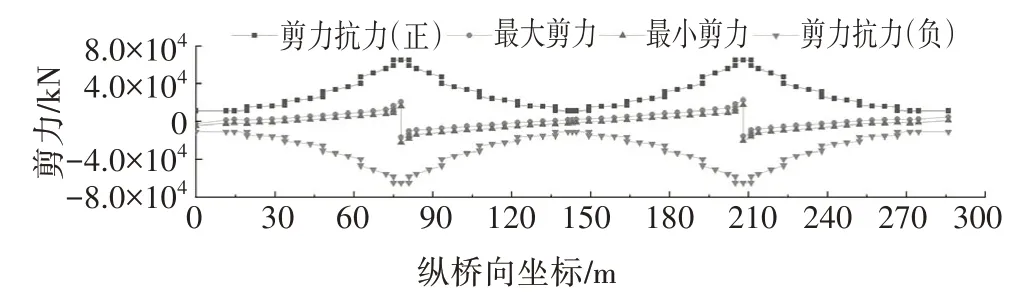
圖7 主梁剪力包絡及抗力圖Fig.7 Shear envelope and resistance of the main girder

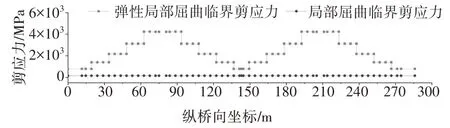
圖8 局部屈曲剪應力Fig.8 Local shear buckling stress

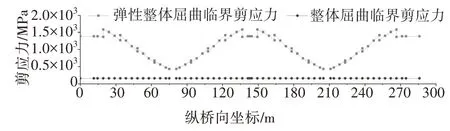
圖9 整體屈曲剪應力Fig.9 Global shear buckling stress

《波形鋼腹板組合梁橋技術標準》（CJJ/T 272—2017）規定CSW 剪應力設計值不應超過組合屈曲臨界剪應力［14］，即：

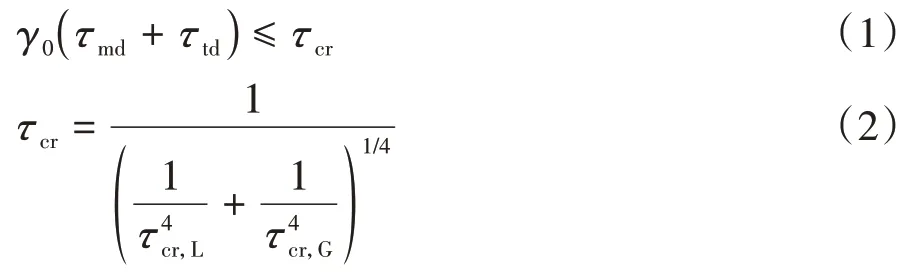
式中：τmd為剪力與預應力的豎向分力產生的剪應力設計值，MPa；τtd為扭矩產生的剪應力設計值，MPa；τcr為波形鋼腹板組合屈曲臨界剪應力，MPa；τcr，L為波形鋼腹板局部屈曲臨界剪應力；τcr，G為波形鋼腹板整體屈曲臨界剪應力.

求得組合屈曲臨界剪應力τcr=155 MPa，剪應力設計值τmax=52.3 MPa.可知試設計方案CSW 承載能力極限狀態剪切穩定滿足規范CJJ/T 272—2017 要求［14］，且具有較大的組合屈曲剪應力富余.

剪力連接件受剪承載力應符合下式要求：

經計算可知，栓釘單位長度水平受剪承載力設計值和水平剪力設計值分別為2 128 N/mm 和1 132 N/mm，栓釘連接件受剪承載力滿足規范要求.

2.2 施工及使用階段應力分析

表3 給出了施工階段和使用階段的應力值，從表中可以看出施工階段應力和正截面壓應力均低于規范T/CCES 27—2021 限值［22］，荷載頻遇組合作用下無拉應力出現，且具有一定的應力儲備.

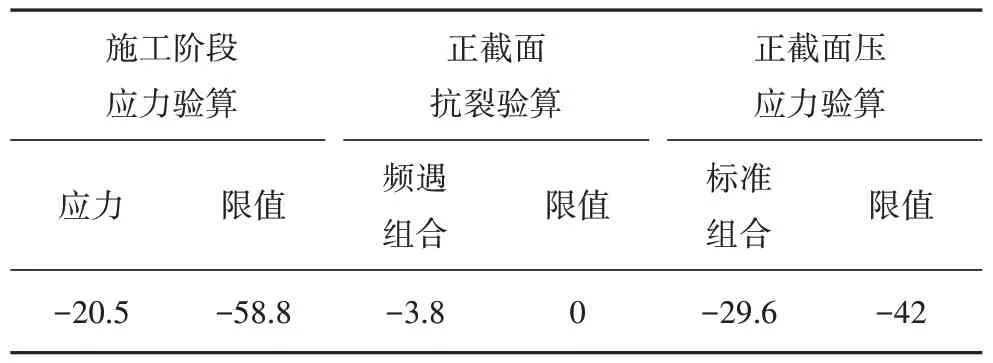
表3 施工及使用階段應力Tab.3 Stresses during construction and service stages MPa

2.3 合理梁高范圍分析

在上述分析中，CSWs-UHPC 組合箱梁橋的梁高取值參考了已建成的主跨為120～150 m 的CSWs-NC組合箱梁橋方案，目前缺少可直接用于CSWs-UHPC組合連續箱梁橋設計的梁高參數.本節在結構靜力分析的基礎上，對CSWs-UHPC 組合箱梁橋中支點和中跨跨中的合理梁高范圍進行分析，以便對主跨跨徑為100～200 m 的CSWs-UHPC 組合連續箱梁橋的結構設計提供可直接參考的合理梁高范圍.

2.3.1 中支點和中跨跨中合理梁高范圍分析

由組合結構內力和應力分析得到中支點梁高的下限值.隨著中支點梁高的降低，中支點負彎矩降低，中跨跨中正彎矩增大.為滿足使用階段抗裂要求，必須增大中跨合攏底板束的數量，可能導致使用階段正截面最大壓應力超過0.5fck=42 MPa［22］.根據計算可得到中支點梁高的下限值為6.0 m，高跨比為1/22.

由撓度計算得到中跨跨中梁高的下限值［22］.分別計算了中支點梁高為6.0 m、6.5 m、7.0 m、7.5 m 時對應的中跨跨中梁高臨界值，計算結果見表4.

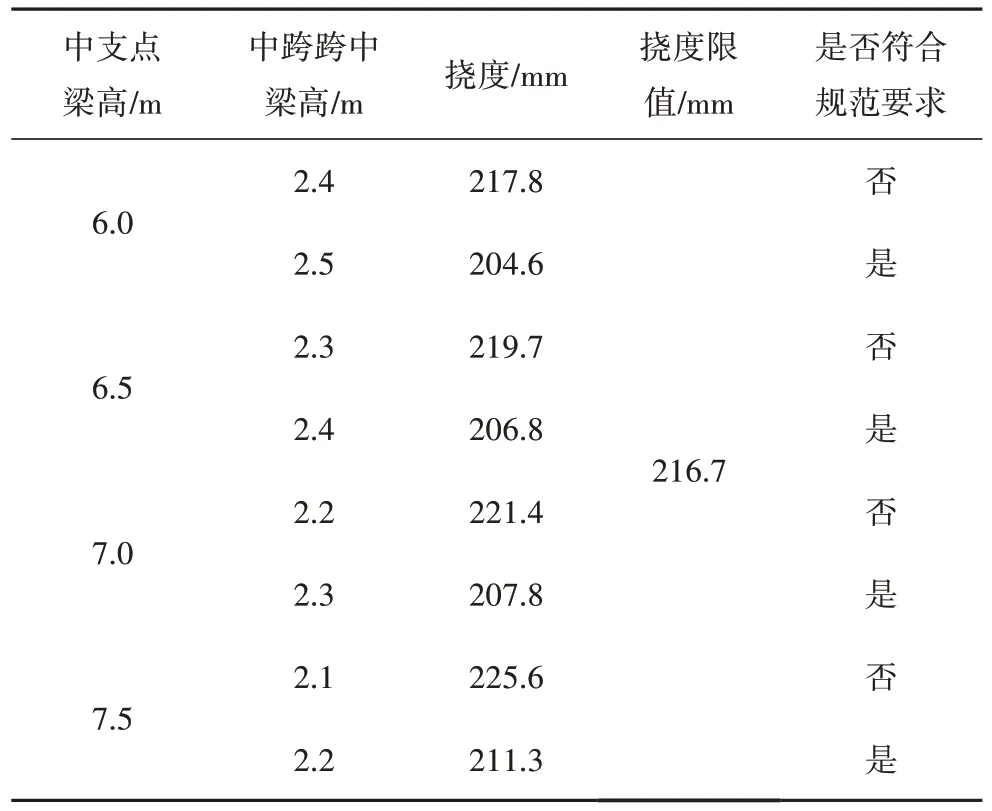
表4 不同梁高組合下主跨跨中撓度Tab.4 Deflection under different combinations of beam depths

由表4 可知：當組合梁中支點梁高為6.0 m、6.5 m、7.0 m、7.5 m 時，中跨跨中梁高的下限臨界值分別為2.5 m、2.4 m、2.3 m、2.2 m.計算得到的中支點梁高與主跨跨徑比和跨中梁高與主跨跨徑比下限值的關系曲線如圖10 所示.從圖10 可以看出：中跨跨中梁高跨徑比的下限值隨支點梁高跨徑比的增大而大致呈線性減小的趨勢，擬合線性方程為Hm/L=-0.2Hs/L+0.029，即中跨跨中與中支點的梁高比為Hm/Hs=-0.2+0.029L/Hs，Hs表示中支點梁高，L表示中跨跨徑，Hm表示由先行確定的中支點梁高推算得到的中跨跨中梁高的下限值.

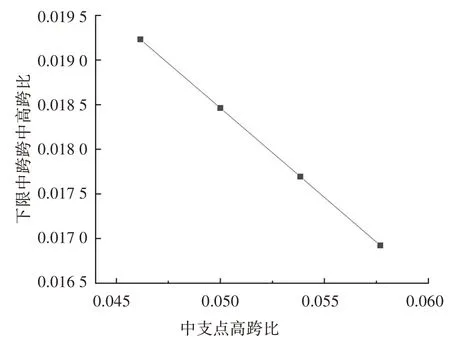
圖10 中支點高跨比-中跨跨中高跨比下限值關系圖Fig.10 Ratio of girder depth at support to mid span length versus the lower limit of the ratio of girder depth at midspan to mid span length

在初始方案的基礎上，增加梁高使中支點附近的波形鋼腹板更容易發生整體屈曲，并且增加用鋼量.參考PC 連續箱梁橋梁高取值范圍的上限值［24］，可得到CSWs-UHPC 組合連續箱梁橋梁高上限值，即中支點梁高與中跨跨徑比Hs/L為1/16，中跨跨中梁高與中支點梁高比Hm/Hs為1/1.5.

綜上可知，CSWs-UHPC 組合連續箱梁橋合理梁高范圍為：中支點梁高與中跨跨徑比Hs/L為1/16～1/22，中跨跨中梁高與中支點梁高比Hm/Hs為1/1.5～（-0.2+0.029L/Hs）.

2.3.2 采用梁高限值的組合橋梁方案受力分析

分別采用合理梁高范圍的上限值和下限值，進行相應CSWs-UHPC 組合連續箱梁橋的受力分析.方案1 取合理梁高范圍的下限值，中支點梁高為6.0 m，中跨跨中梁高為2.5 m；方案2 取合理梁高范圍的上限值，中支點梁高為8.1 m，中跨跨中梁高為5.4 m.計算結果如表5所示.

表5 采用梁高臨界值的CSWs-UHPC組合結構應力Tab.5 Stresses of the CSWs-UHPC composite plans with critical depths MPa

從表5 可以看出：當分別采用合理梁高范圍的上限值和下限值時，CSWs-UHPC 組合箱梁橋的受剪承載力和使用階段應力均滿足規范要求［9，14］.在進行CSWs-UHPC 組合箱梁橋結構設計時，梁高取值可參考本文提出的合理梁高范圍.

將2.3.1 節中得到的CSWs-UHPC 組合箱梁橋合理梁高范圍與PC 箱梁橋和CSWs-NC 組合箱梁橋的中支點及中跨跨中梁高設計建議值［15，24］進行對比可知：CSWs-UHPC 組合箱梁橋中支點及中跨跨中梁高的下限值小于PC 連續箱梁橋和CSWs-NC 組合箱梁橋.這是因為CSWs-UHPC 組合箱梁橋的自重顯著降低，中支點負彎矩和跨中正彎矩大大減小，在合理范圍內降低梁高可滿足承載力要求.并且本設計方案中所采用的UHPC 的抗壓強度標準值是C50 混凝土的2.6 倍，在使用階段可承受更大的正截面壓應力.因此，當跨徑和荷載條件相同時，CSWs-UHPC 組合箱梁橋的梁高取值可小于CSWs-NC 組合箱梁橋和PC箱梁橋.

3 動力性能分析

為探究CSWs-UHPC 組合連續箱梁橋的動力特性，分別建立了CSWs-NC 組合箱梁橋、PC 連續箱梁橋以及CSWs-UHPC 組合連續箱梁橋的有限元模型，并考慮了下部結構尺寸變化的影響，對不同橋梁方案的動力特性和在E2 地震作用下的非線性動力時程進行了對比分析.

3.1 模型概況

CSWs-UHPC 組合箱梁橋A、CSWs-NC 組合箱梁橋及PC 箱梁橋采用相同的下部結構方案，布置情況為：1#、4#橋墩高19 m，采用矩形空心截面，邊長為8 m×2.6 m，壁厚0.8 m；2#、3#橋墩高15 m，采用邊長8 m×5 m 矩形空心截面，壁厚1.0 m，如圖11、圖12（a）所示.為符合工程實際，CSWs-UHPC 組合連續箱梁橋B采用截面尺寸縮減的主墩.由于CSWs-UHPC組合箱梁橋上部結構自重比PC 箱梁橋降低了54%，所受的汽車制動力與PC 箱梁橋相同，綜合考慮，CSWs-UHPC 組合箱梁橋B 的2#、3#橋墩采用邊長8 m×4 m 矩形空心截面，壁厚0.8 m，如圖12（b）所示，1#、4#墩則與其他三種方案相同.各橋梁方案的橋墩橫截面尺寸如表6 所示.建立的有限元模型忽略了樁土的相互作用，各墩底在地面處固結.

圖11 橋墩與支座布置圖（單位：m）Fig.11 Layout of piers and supports（unit：m）

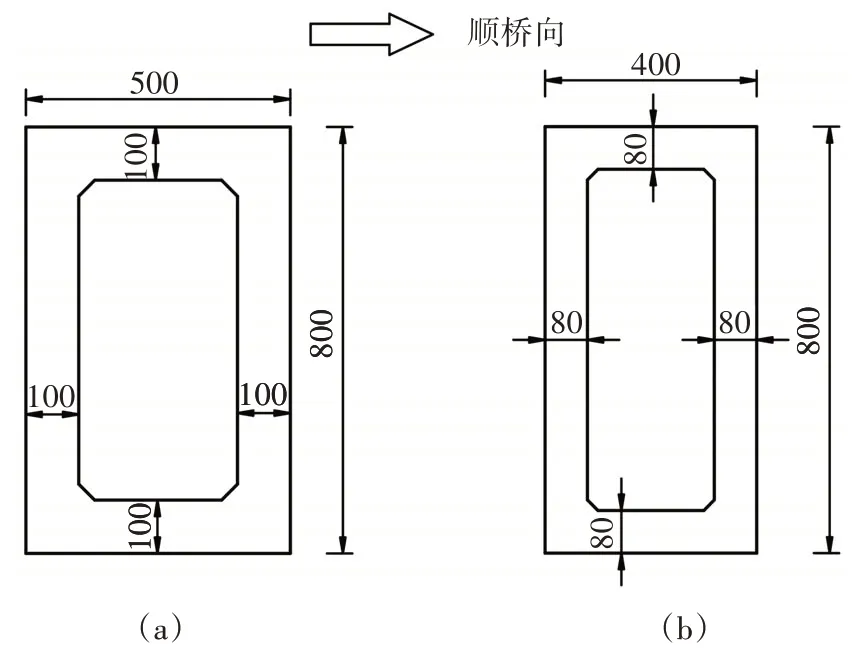
圖12 主墩截面布置（單位：cm）Fig.12 Typical cross section of main pier（unit：cm）

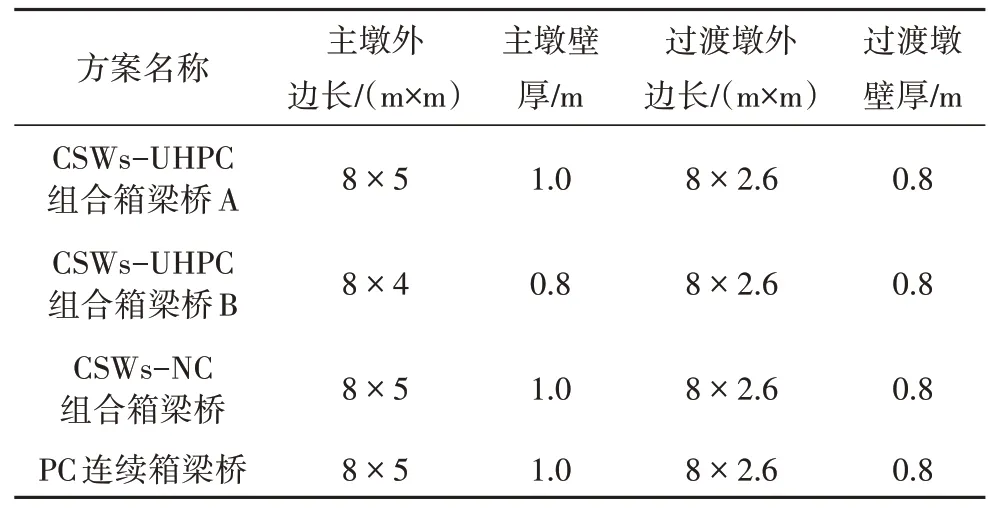
表6 橋墩橫截面尺寸Tab.6 Cross section dimension of pier

在1#和4#墩頂設置LNR 矩形滑動型支座；2#和3#墩頂設置HDR（I）型隔震高阻尼橡膠支座.HDR 支座和LNR 支座的滯回模型如圖13 所示.2#、3#墩頂的HDR 支座帶有剪力鍵，在正常使用和常遇地震狀況下，剪力鍵起到限制主梁位移的作用；而在罕遇地震下，剪力鍵可“熔斷”，隔震高阻尼橡膠支座通過較大的水平剪切變形能力耗散地震能量［25］.

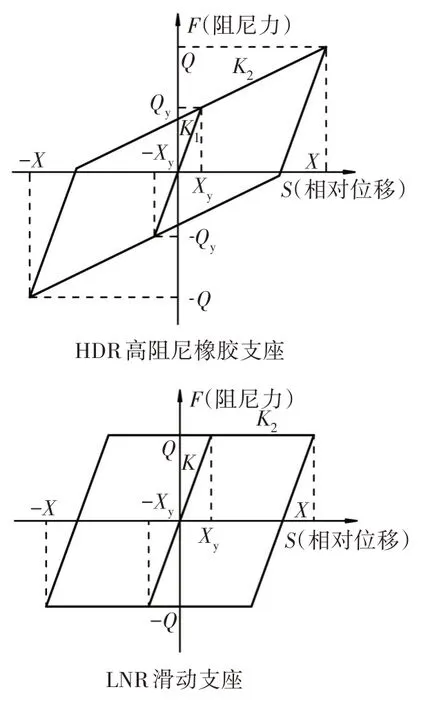
圖13 支座滯回模型Fig.13 Hysteretic model of bearings

3.2 地震波選擇

地震荷載工況為：分區特征周期0.4 s，場地類型Ⅱ，設防烈度8（天然地震波峰值加速度為0.3g）［26］.計算得到E2 地震設計加速度反應譜最大值Smax=1.275g.根據設計加速度反應譜E2，采用SIMQKEGR 軟件，分別生成E2 人工地震波3 條，地震波峰值加速度為0.51g，持續時間均為40 s，E2 人工地震波如圖14 所示.由于橫橋向地震作用下橋墩的內力和位移較小，本文僅考慮2#制動墩在縱橋向地震波作用下的內力響應.

圖14 E2人工地震波Fig.14 E2 artificial seismic wave

3.3 自振頻率與振型

4 種橋梁方案的自振頻率與振型特征如表7 所示.由表7 可以看出：對于第1～第5 階振型，CSWs-UHPC組合箱梁橋A與CSWs-UHPC組合箱梁橋B的自振頻率基本相同.4種橋梁方案的第1階振型均表現為主梁橫向彎曲，CSWs-UHPC 組合箱梁橋的自振頻率最低，為0.260 Hz；CSWs-NC 組合箱梁橋的自振頻率與CSWs-UHPC 組合箱梁橋相差較小，為0.272 Hz；PC 箱梁橋自振頻率最高，為0.490 Hz.這是因為CSWs-UHPC 與CSWs-NC 組合箱梁橋采用波形鋼腹板，抵抗橫向彎曲的能力較弱.

CSWs-UHPC 組合箱梁橋第1、2、4 階為橫向彎曲，第5階為豎向彎曲；CSWs-NC組合箱梁橋第1、3、5 階為橫向彎曲，第4 階為豎向彎曲；PC 箱梁橋第1、2階為橫向彎曲，第4、5階為豎向彎曲，表明3種方案的橫向抗彎剛度均弱于豎向抗彎剛度.振型為一階豎彎時，CSWs-UHPC 組合箱梁橋的頻率最大，說明CSWs-UHPC組合箱梁橋的豎向抗彎剛度最大.

3.4 下部結構相同的3種方案地震響應

表8 為下部結構相同的3 種方案在E2 地震波作用下2#橋墩墩底彎矩峰值、剪力峰值以及梁端位移峰值.從表8 中的數據可以看出：CSWs-UHPC 組合箱梁橋的彎矩峰值、剪力峰值以及梁端位移峰值均小于CSWs-NC 組合箱梁橋和PC 箱梁橋；CSWs-UHPC 組合箱梁橋A 的墩底彎矩峰值對比CSWs-NC組合箱梁橋和PC 箱梁橋分別降低了20%和31%；其墩底剪力峰值對比CSWs-NC 組合箱梁橋和PC 箱梁橋則分別降低了22%和29%.這是因為CSWs-UHPC組合箱梁橋上部結構自重相比CSWs-NC 組合箱梁橋和PC 箱梁橋分別降低了45%和54%，使得地震作用下的慣性力大幅降低，因此墩底的彎矩和剪力也顯著降低.

從表8 中的數據還可以看出：CSWs-UHPC 組合箱梁橋梁端縱向位移對比CSWs-NC 組合箱梁橋和PC箱梁橋分別降低了25%和23%.CSWs-NC組合箱梁橋與PC 箱梁橋梁端縱向位移峰值僅相差3%，而CSWs-NC 組合箱梁橋的自重比PC 箱梁橋降低了16.6%，原因是PC 箱梁橋一階縱飄對應的自振頻率較大（見表7），地震作用下位移響應降低，從而抵消了由于較大的慣性力而增加的位移響應.

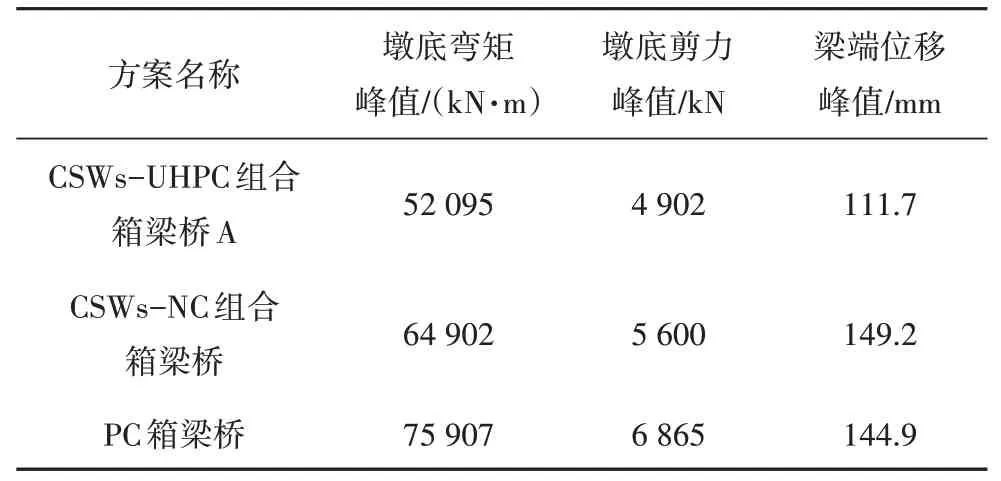
表8 地震響應對比Tab.8 Comparisons of Seismic responses

圖15 所示為E2-1 地震波作用下中墩支座的滯回曲線.CSWs-UHPC 組合箱梁橋支座位移、水平力及滯回曲線包圍面積小于CSWs-NC 組合箱梁橋和PC箱梁橋，相比CSWs-NC組合箱梁橋和PC箱梁橋，CSWs-UHPC 組合箱梁橋支座滯回曲線包圍的面積分別降低了41.3% 和49.0%.在地震波激勵下，CSWs-UHPC組合箱梁橋需要耗散的能量大大降低.

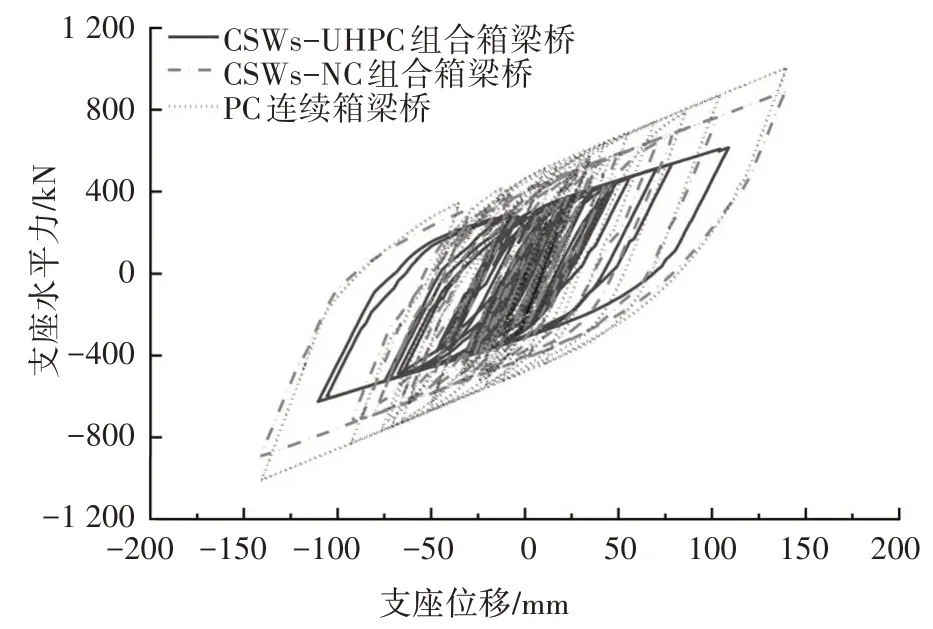
圖15 支座滯回曲線Fig.15 Hysteretic curves of bearing

3.5 下部結構不同的組合箱梁橋地震響應

由圖16 可以得出：CSWs-UHPC 組合箱梁橋A與CSWs-UHPC 組合箱梁橋B 的支座滯回曲線基本重合.

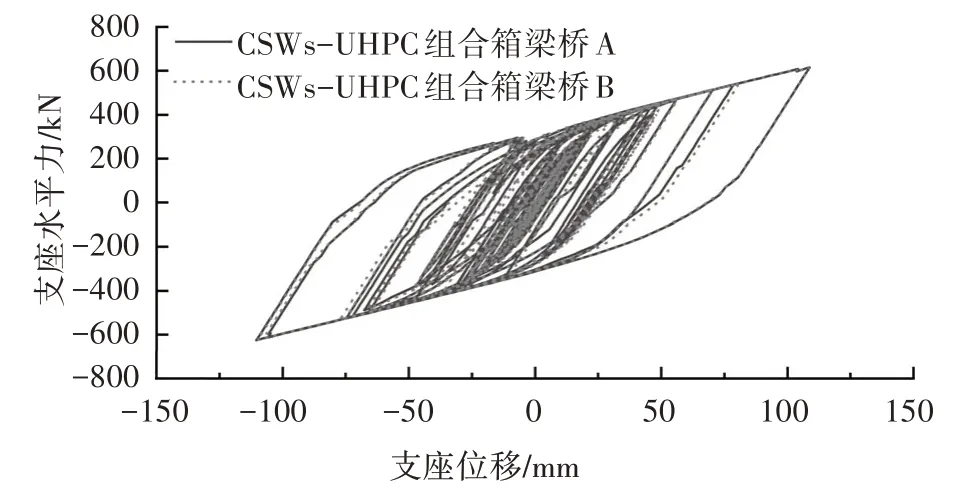
圖16 CSWs-UHPC組合箱梁橋支座滯回曲線Fig.16 Hysteretic curves of bearing of CSWs-UHPC composite box girder bridges

當主墩橫截面尺寸不同時，表9 給出了CSWs-UHPC 組合箱梁橋在E2 地震波作用下2#橋墩墩底彎矩峰峰值、剪力峰值以及梁端位移峰值.從表9 中的數據可以看出：CSWs-UHPC 組合箱梁橋B 的墩底彎矩和剪力峰值對比CSWs-UHPC 組合箱梁橋A 分別降低了10%和14%.由于CSWs-UHPC 組合箱梁橋A、B 主墩的支座滯回曲線基本重合，即2#、3#橋墩墩頂所受的支座水平力基本相同.2#、3#橋墩截面尺寸減小后，橋墩的縱橋向彎曲剛度和重量降低，在地震荷載及支座水平力的作用下，墩底彎矩和剪力降低.但CSWs-UHPC 組合箱梁橋A 與CSWs-UHPC 組合箱梁橋B的梁端位移峰值基本相同.

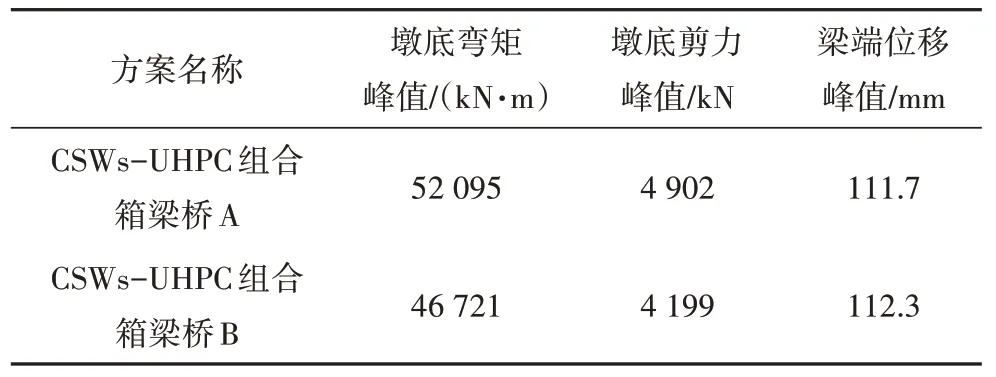
表9 CSWs-UHPC組合箱梁橋地震響應對比Tab.9 Comparisons of Seismic responses of CSWs-UHPC composite box girder bridges

由以上分析可以得出：在E2 地震波作用下，CSWs-UHPC 組合箱梁橋可降低梁端位移以及中墩墩底處的彎矩和剪力，使得隔震橡膠支座所需要消耗的能量顯著降低.CSWs-NC 組合箱梁橋和PC 箱梁橋在地震荷載作用下的縱向位移較大，需要設置一定數量的阻尼器以減小縱向位移；而CSWs-UHPC組合箱梁橋可不設阻尼器或僅設置較少數量的阻尼器即可滿足結構抗震的需求.

4 結論

本文利用UHPC 的高強度、高韌性的特點，設計了一座大跨徑全體外預應力CSWs-UHPC 組合連續箱梁橋，對其進行了結構靜力和抗震性能分析，并將其與CSWs-NC 組合箱梁橋及PC 連續箱梁橋進行對比，得到如下結論：

1）對比CSWs-NC 組合箱梁橋和PC 箱梁橋，CSWs-UHPC 組合箱梁橋的自重分別降低了45%和54%，CSWs-UHPC 組合箱梁橋的使用荷載作用效應占總效應的比例分別提高了66.9%和91.8%，對提升連續梁橋主跨跨越能力具有較大潛力.

2）CSWs-UHPC 組合箱梁橋上部結構自重的大大降低，能進一步減少下部結構的工程量，降低運輸吊裝成本，且UHPC 在橋梁運營期不需要養護，CSWs-UHPC 組合箱梁橋全壽命周期成本具有一定的優勢.

3）130 m 跨徑波形鋼腹板-UHPC 組合箱梁橋合理梁高范圍為：中支點高跨比Hs/L=1/16～1/22，中跨跨中梁高與中支點梁高比Hm/Hs=1/1.5～（-0.2+0.029L/Hs）.

4）由于CSWs-UHPC 組合箱梁橋上部結構自重較輕，慣性荷載大大降低，地震響應顯著降低；CSWs-UHPC 組合箱梁橋可不設阻尼器或僅設置較少數量的阻尼器即可滿足結構抗震的需求.

綜上所述，CSWs-UHPC 組合箱梁橋具有良好的全壽命周期經濟性和靜力性能，其自重、結構有效性和抗震性能對比CSWs-NC 組合箱梁橋和PC 箱梁橋均具有明顯優勢，是大跨徑連續梁橋中一種有較強競爭力的結構型式.