格拉頓-吉尼斯的HPM思想*

徐伯華

(南通大學教育科學學院 226019)

朱鳳琴

(南京信息工程大學無錫學院數理學院 214105)

艾弗·格拉頓-吉尼斯(Ivor Grattan-Guinness,1941—2014)，英國米德爾塞克斯(Middlesex)大學數學史教授，一生致力于數學和數理邏輯的歷史研究，2009年因“終身學術成就和貢獻”與R.C.Gupta分享國際數學史學會凱尼斯·梅獎．在四十多年的職業生涯中，格拉頓-吉尼斯一直重視數學史的教育價值，不斷思考數學史服務數學教育的問題，形成了獨特的HPM思想．有評論說：他的思想隨著時間的推移而逐漸成熟、逐漸拓展，雖具有一般主題上的統一性，但并不是鐵板一塊[1]，主要是理論性的、指導性的[2]．由于格拉頓-吉尼斯是一位專業的數學史家，并不專門研究HPM，有關HPM的論述散見于他的論文、評論、報告中，國內還沒有系統的研究．本文運用文獻研究法，以他的四篇文獻[3-6]為主要研究對象，結合其他文獻和評論，從思想基礎、數學史的地位、解讀數學史的方式、融入數學史的方法四個方面整理、概括他的HPM思想，希望給我國HPM

[2] 徐超．拋物線概念教學:重構數學史[J]．教育研究與評論(中學教育教學)，2015(8)：26-31．

[3] 張佳麗．HPM視角下高中圓錐曲線的教學研究[D]．南昌：江西師范大學，2018．

[4] 陸琳琰．拋物線的發生教學研究[D]．上海：華東師范大學，2013．

[5] Tanner J H,Allen J.An elementary course in analytic geometry[M].New York:American Book Company,1898：67-68.

[6] Salmon G.A treatise on conic sections[M].Dublin:Hodges & Smith,1850：120-124.

[7] Smith P F,Gale A S.New analytic geometry[M].Boston:Ginn,1912:153.

[8] Ziwet A,Hedric E R,Hopkins L A.Analytic geometry and principles of algebra[M].New York:The Macmillan Company,1913：131.

[9] Roberts M M,Colpitts J T.Analytic geometry[M].New York:John Wiley & Sons,1918:110-119.

[10] Harding A M,Mullins G W.Analytic geometry[M].New York:The Macmillan Company,1926:120-124.

[11] Loomis E.Elements of analytical geometry and the differential and integral calculus[M].New York:Harper & Brothers,1851:44-53.

[12] Phillips H B.Analytic geometry[M].New York:John Wiley & Sons,1915:74-77.

[13] Bauer G N.The simpler elements of analytic geometry[M].Minneapolis,The H.W.Wilson Company,1903:38-41.

[14] Poor V C.Analytical geometry[M].New York:J.Wiley & Sons,1934:82-102.

[15] Reynolds J B,Weida F.Analytic geometry and the elements of calculus[M].New York:Prentice-Hall,1930:153-159.

[16] Biot J.An elementary treatise on analytical geometry[M].Philadelphia:Charles Desilver,1860：95-139.

[17] Loomis E.The elements of analytic geometry[M].New York:Harper & Brothers,1872:84-102.

[18] Smith P F,Gale A S.The elements of analytic geometry[M].Boston:Ginn & Company,1904:173-178.

[19] Hamilton H P.The principles of analytical geometry[M].Cambridge:J.Deighton & Sons,1826:142-143.

[20] Robinson H N.Conic sections and analytical geometry[M].New York:Ivison,Blakeman & Company,1860:50.

的理論和實踐帶來啟發和幫助．

1 思想基礎：數學知識并非憑空產生

格拉頓-吉尼斯之所以從事數學史研究，緣自他對數學教育的不滿．早在20世紀60年代，他就感到數學教學多是按照整理好了的、嚴格的數學理論進行的，很少討論問題的核心動機，甚至不討論相關的歷史發展與人的作用．四十多年后，他仍然說：“我的研究動機完全來自于對數學教育的消極反應……展現在我面前的是一系列令人贊嘆的數學理論，但是為什么首先要研究這些理論？為什么教授方式差強人意？它們從哪里來的？沒有人能在某個周四的下午坐下來，像教給我們的那樣發明群論．”[7]

這種不滿促使他思考數學的來源，思考數學史對數學教育的價值．他意識到，這些問題本身不是數學問題，而是數學哲學問題．于是，他向大名鼎鼎的波普爾(Karl Popper)求教，選修了碩士課程，攻讀了博士學位，分別于1969年、1978年獲得倫敦大學數學史哲學博士學位和科學史與科學哲學理學博士學位，從此走上數學史與邏輯史的研究道路．波普爾的科學觀對格拉頓-吉尼斯影響很大，在梅獎發言中他還特別提到了以下幾點：生命是一個問題解決的過程；科學總是處于猜想、驗證、理論化的過程中；知識的生長比知識本身更重要；知識的基礎是挖掘出來的，而不是建立其上的；認識不僅包括知的根源，還包括不知的根源；未來是開放的，既是主觀的又是客觀的．[7]

格拉頓-吉尼斯認為，數學知識不是憑空產生的，一個知識生長出另一個知識，有復雜而深刻的路徑．對一個現代形式的數學知識，如果不了解它的發生動機、不了解它的發展過程，就不可能深刻地理解它．例如，作為數學基礎的“集合”，看似簡單，但要很好地理解它，絕非易事．康托既不是唯一、也不是首先研究集合的數學家，他的研究起源于黎曼的三角幾何級數．在考察非收斂的“點集”與特殊級數間的關系時，他得出了兩類非收斂點，由此定義了集合的類型，證明了連續統無限大于可數集，給出了超限算術的序數列，這是康托研究無限集的序、定義集合的勢的真正起點．為了把有限算術和超限算術建立在一般的集合概念上，康托提出了樸素的集合定義，從而擺脫了序，建立了基數算術，并逐步使集合論成為測度論、分析學以及數學基礎研究的有力工具．現在的教材只呈現加工好的、簡化的集合理論，雖然讓人容易接受，卻不能讓人領悟到它的優越性．

同樣地，對一個現代形式的數學知識，如果沒有相應的方法論支持，我們也不可能深刻地理解它．例如，很多人認為數學知識總是正確的，數學有可靠的基礎，人們信任數學，就像信任歐幾里得幾何一樣，這被稱為歐幾里得主義．隨著現代數學的發展，數學的基礎不在于定義是不是正確，而在于基本要素的一般性和簡單性，數學重視的不再是不變的事實，而是不變的結構，人們對數學的可靠性、嚴謹性的認識發生了改變，這被稱為新歐幾里得主義．歐幾里得主義、新歐幾里得主義都不是數學知識本身，而是數學的方法論．方法論在數學體系中很重要，它決定著我們如何理解數學．例如，可誤主義主張數學知識是在嘗試中被接受的，其標準是能否成功地解決問題，除非一個技術性知識需要一個基礎，否則就不存在基礎知識．在這種觀念下，數學知識就沿著技術和基礎兩個方向生長起來，表現出不同的層次和深度．要想很好地理解一個數學知識，就要熟悉它的基礎性知識、技術性知識、方法論知識、認識論知識，這絕不是知識本身所顯現的那么簡單．

生長的觀點、歷史的觀點能讓我們看到數學知識的豐富性，從而更加深刻、更加準確地理解它．如果刻意簡化數學，不僅會使知識膚淺化，還會讓人難以理解，給人留下一個壞印象：數學就是用不平常的方式觀察平常的事情．格拉頓-吉尼斯喜歡用“演進”(Convolution)解釋數學的發展，而不是“革命”(Revolution)．他認為，數學的發展從沒有完全顛覆前期的成果，演進包括創新和替代，是一個認可、接受、拒絕、修正的動態過程，當談到某個數學知識時，就不僅包含這個知識本身，還涉及與之相關的其他知識．例如：

(1)定義包含更多知識

數學定義并不是簡單的命名方式，它所使用的判斷和概念，要么是不明確的，要么是有定義的，要想很好地理解它，就要弄清楚這些判斷和概念，以及凸顯這些判斷和概念之所以重要的那些語句．一些原創的定義為定理提供了證明，或者是公理的一種形式，其確切的意義只有通過重新解釋定理或公理才能獲得．

(2)數學理論有多個層次

對一般的數學知識來說，理性主義、經驗主義是認識論知識，實證主義、可誤主義是方法論知識．通常情況下，一般的數學知識包含于認識論知識之中，認識論知識又包含于方法論知識之中．數學理論就是由一般的數學知識、數學的認識論知識、數學的方法論知識構成的多層次的復雜體系．

(3)數學有三種表述

一是認識論表述，是由基本原理演繹出的形式系統，典型的是公理化系統．二是歷史的表述，通過描述不同階段的發展進程，如創造的發現過程、學術的影響過程等，歷史地反映數學知識和數學理論．三是啟發式表述，即從熟悉的情境中激發動機，獲取實例，然后經過猜想、驗證等一系列活動，最終在啟發和思考中生成理論．認識論表述往往基于最新的觀點去解釋、梳理已有的知識．歷史的表述則相反，往往挖掘更深的基礎和背景，解釋知識的由來．而啟發式表述介于兩者之間，既有認識論成分也有歷史成分，在生成理論的同時，也帶來更多的啟發和思考．

2 數學史的地位：數學學習中的積極角色

數學知識不是憑空產生的，數學史在背后支撐著學生的學習和理解．你可以不關心數學史，不喜歡數學史，但不可能不受數學史的影響．在數學學習中，數學史是一個積極角色．與其討論是否用數學史，還不如討論如何自覺地運用數學史．數學史的積極角色具體表現為：

(1)模仿的對象

從某種意義上說，數學學習是數學研究的模仿．學生了解數學知識的早期發展，模仿數學的研究過程，不僅能獲得知識，還能獲得學習的途徑和方法．模仿的對象有很多，如目標選擇的背景、思路發現的途徑，甚至曾經發生過的各種錯誤和策略．當然，模仿應該是啟發式模仿，不能只是認識論模仿，因為認識論模仿更多地關心數學的結果，其價值是有限的．

(2)體驗的素材

數學學習要獲得知識，但更重要的是經歷、體驗一些創造性活動．如果學生面對數學史上的一個獨創性問題，從不熟悉的情景開始，重構發明創造的過程，感受觀念的萌生、發展和衰落，就會切實體會到數學的精神、思想和方法，看到數學活動中的“人”的真實世界．借鑒數學史，給學生一個真實的問題，雖然有可能增加學生的困難，但對學生的學習和發展是有深遠意義的．

(3)研究的內容

數學大家對數學史往往情有獨鐘，他們認為如果一個觀點很重要，那么其歷史也就很重要，與之相關的因素就要仔細考察，然后才可能推進它．數學大家喜歡數學史不是被動的，他們知道要想做好數學，只能從歷史中學習，沒有別的辦法．在數學學習中，數學史不是可有可無的陳詞濫調，它應該成為數學學習的內在成分，通過研究前人的成就，了解更多的知識，激發創造的靈感，逐漸作出自己的貢獻．

(4)學科理解的途徑

形式化的數學有解無問、有答無疑，看不到“人”；編年體的數學能指出數學家的成就和局限，但常常以此評價后人；而實證主義能說明一個概念為什么重要，但彰顯的是后來的觀點，缺乏靈活性和廣泛性．在數學學習中，上述方式都是需要的，把它們合在一起，才能體現出“人”的活動和價值．實際上，數學學習的內容不是那么重要，與之相聯系的方法論更有價值．方法論可以解決不同的問題，越是自覺地使用它，越會得到更好的發展．數學史既包含數學的知識，又包含數學的方法論，既有科學性，又有人文性，對學生理解數學學科、感受數學文化、提高數學素養，都是至關重要的．

(5)啟發動機的資源庫

在知識和理解之間，數學史傾向于理解，通過提供動機、檢驗知識背后的發展和相互關系，幫助學生樹立問題意識、調動研究興趣、提高認識水平．成功的數學教育離不開深刻的、深入的思考動機，數學史上的問題、背景、應用、影響、不同層次的嚴謹、數學與其他學科的互動，都是啟發動機的資源．甚至曾經發生的各種錯誤也是很好的動機資源．要知道，數學本來就是人類的一項活動，致力于解決有趣的問題，犯錯在所難免，數學大家的一個錯誤往往比普通人做出的一百個無懈可擊的小定理，更具有影響力和啟發性．

3 解讀數學史的方式：歷史與遺產

對同一個數學史料，不同的人可能有不同的解讀．例如，同樣是讀《原本》，史學家會發現，歐幾里得處理的對象是線而不是長度，是平面區域而不是面積，而數學家則會融入方程的思想，從中讀出幾何代數來．格拉頓-吉尼斯認為，圖形的解讀和方程的解讀都是合理的，沒有對錯之分，但卻彼此不同，前者稱為歷史的解讀方式，后者稱為遺產的解讀方式．

一般地，如果兩個數學對象A,B有聯系，并且A的出現早于B，就稱A是B的歷史；反之，稱A是B的遺產．例如，方程對于歐幾里得來說是遺產，對于笛卡爾來說是歷史．

歷史的解讀方式，關注數學對象在特定時期的發展，包括它的前史、提出、早期形態、年表、內外影響與應用等，主要通過對過去的描述和解釋來回答這樣的問題：過去發生了什么？過去沒發生什么？為什么會發生？為什么沒有發生？數學史家常用歷史的解讀方式，希望在更廣泛的意義上尋找數學活動的動機、根源、成果．

遺產的解讀方式，關注數學對象對后期或者現在的影響，主要回答的問題是：我們是怎樣來到這里的?給出的答案往往像一條康莊大道，似乎后期的成果早就蘊藏在前期的形態和觀念之中了．實際上，這是對史料注入后期觀念的結果．數學家常用遺產的解讀方式，希望從過去的數學中獲得現在需要的思想靈感．

通常情況下，一個數學對象既有自己的歷史，也有自己的遺產．數學教育在歷史資源和遺產資源的選擇上，應該選擇最能發揮教育效益的資源，而不是偏執一端．例如，在代數教學中，《原本》中的幾何代數最能發揮效益，那就用它的遺產資源，或者說遺產地應用它；在幾何教學中，線和面的幾何最能發揮效益，那就用它的歷史資源，或者說歷史地應用它；而比例理論，既有助于幾何教學，也有助于算術教學，那就根據教學的需要，既可以歷史地應用它，也可以遺產地應用它．

格拉頓-吉尼斯對兩種解讀方式作了細致的區分．表1列出其中的一部分，這部分區分對教師解讀具體的數學史料和資源選擇可能有直接的幫助．

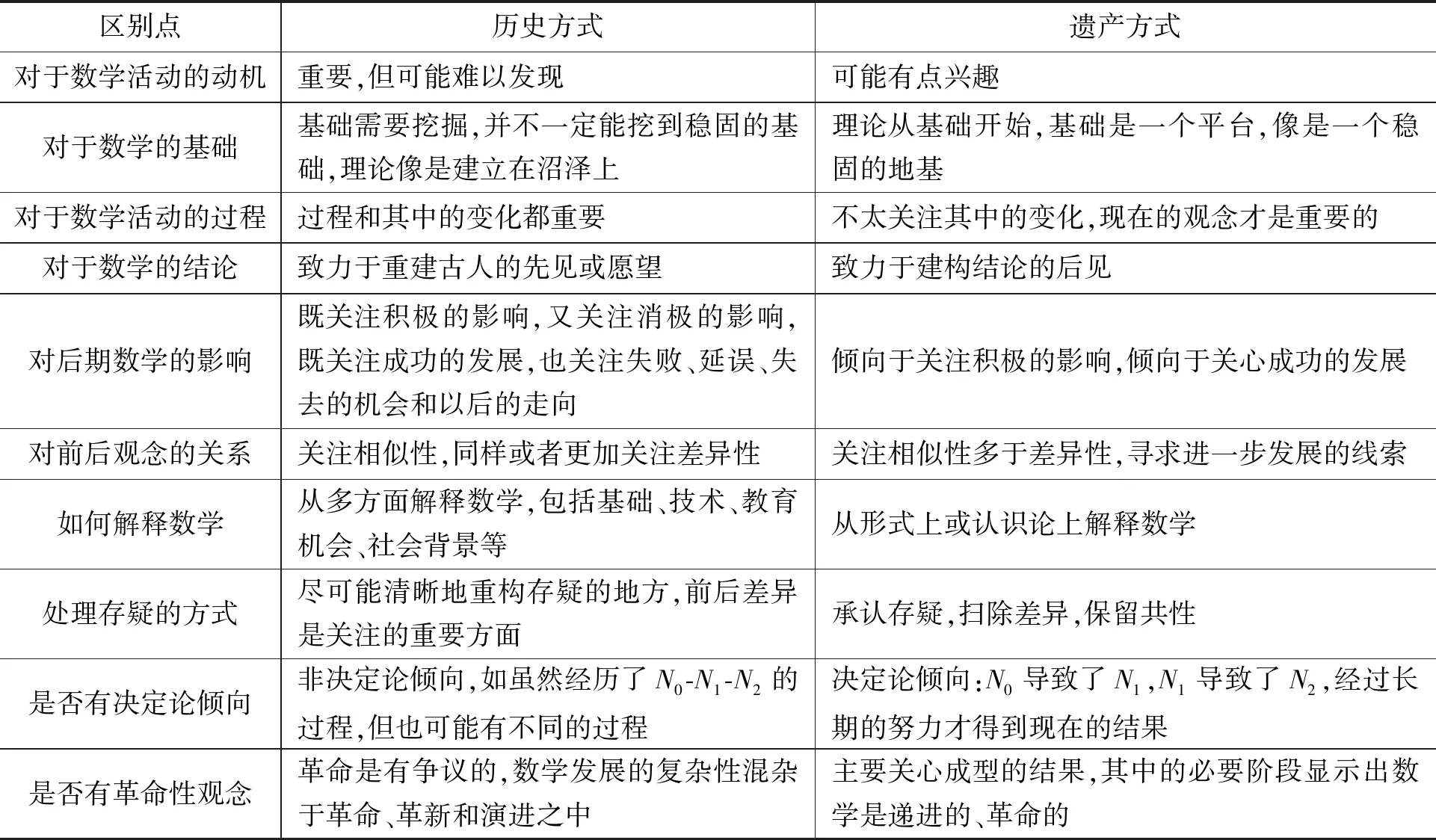
表1 歷史方式與遺產方式的區別

4 融入數學史的方法：“歷史-諷刺”教學法

格拉頓-吉尼斯認同歷史發生原理，他說“教育模仿歷史”，這樣的例子比比皆是．例如零、分數、負數、未知數、常數、變量、方程、函數、極限、向量空間、線性代數、算術運算、超限算術等等．甚至對數學符號，也不能只講授普遍使用的那一個，不同的符號有不同的歷史，所有的符號都應該適當關注．

歷史的或者發生學的方法，不僅能幫助學生深入地理解數學的動機、問題、概念及其聯系，還能幫助教師清楚地表達、應對學生學習的困難，設計合理的教學活動．為了更好地發揮數學史的教學效益，格拉頓-吉尼斯提出以下教學策略：

(1)精選數學問題，圍繞問題展開教學

問題的歷史不一定顯性呈現，但必須有足夠的思考寬度，能廣泛聯系有關學科，讓學生體會到問題的重要性．

(2)解釋問題及其解答的重要階段

說明每個階段的發展貢獻和外部因素，如果有可能，還可以指出該問題發展到現在的路徑，或者指出現在還沒有解決的有關問題．

(3)讓學生在改造的歷史情境中做出一些新結論

教學不必模仿繁瑣的歷史細節，可以給學生提供一定的知識基礎或方法基礎，讓學生自己 尋找更多的細節和興趣，或者從歷史發展的某個中間環節開始，讓學生自己探索解題的途徑和目標．

(4)適當點撥方法論

通過方法論的提示和說明，讓學生感受數學創造的不確定性、知識生長的雙向性、數學理論的層次性，感悟數學的精神、思想和方法，體驗“人”的活動和價值．

“歷史-諷刺”法(history-satire)，是格拉頓-吉尼斯根據自己的教學經驗提出的一種獨特的數學史融入教學的方法．在這里，“歷史”指的是數學史資源，包括歷史資源和遺產資源；“諷刺”指的是借助數學史資源激發學生的動機和思考，突出數學的意義，增強學生的數學理解．

該方法包括兩個基本步驟：一是把歷史文獻翻譯成當前的等價形式，便于學生理解原文、把握數學內容；二是把當前的教學內容嵌入到歷史情境中，讓學生在重構的歷史情境中開展數學活動、實現教學目標．可以看出，該方法有明顯的遺產傾向，第二步不可能完全符合歷史的情景和進程，也不可能把當前教學的知識完全嵌入到歷史情境中去，這是“歷史-諷刺”法的特殊之處．

案例柯西閉線積分定理的教學．

柯西閉線積分定理：具有連續導數的單值可微函數在閉線C上的積分為0．很多學生對這個定理感覺奇怪，教材上利用柯西-黎曼方程和格林公式給出的快速證明更讓學生一頭霧水．

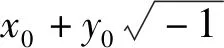
融入數學史的教學思路：實函數的積分定義早已講過，學生比較熟悉．本定理的教學引入上述中間版本，能使學生在實分析的基礎上更容易地理解該定理，這是一次“歷史-諷刺”；而從中間版本到最后版本，能使學生在理解的基礎上超越幾何方式，更深刻地感受到分析的本質，這又是一次“歷史-諷刺”．在兩次諷刺中，教師還可以放大某些歷史要素的意義，以便增強諷刺的效果．例如，把“幾何的角色”作為一個問題提出來，讓學生討論，可以使學生更好地體會圖形在分析中的地位和作用；把“柯西是否假設了f的導數是連續的”作為一個問題提出來，讓學生思考，可以使學生更好地辨析殘數定理的柯西版本與后來版本的不同．

“歷史-諷刺”法的優點很突出，能夠廣泛地關注數學知識的歷史資源和遺產資源，特別有益于當前教學的歷史要素，既讓歷史服務于教學，又不讓教學止步于歷史、局限于歷史．但是，缺點也很明顯，一是諷刺的作用指向數學能力的培養，對基礎概念的學習或者低年級的學習似乎不太合適；二是遺產的傾向容易導致歷史失真，甚至歷史曲解，讓學生對數學學習尤其對數學研究產生偏見，從而不利于學生的長遠發展．不過，這些缺點并非沒法克服，只要教師善加應用，還是能很好地發揮數學史的積極作用的．