改進A＊算法的水面艦艇靜態航路規劃

武善平，黃炎焱，陳天德

南京理工大學 自動化學院，南京 210094

由于海洋環境的復雜性，航路規劃是船舶智能引導的重要組成部分，主要功能是在已知船舶準確位置以及周圍靜態障礙物信息的環境中，搜索一條從起點到終點的、滿足一定要求的航行路徑，使船舶在航行過程中能夠安全可靠地避開所有障礙區域并且使航路盡可能短、盡可能平滑。

路徑規劃問題較早應用于自主移動機器人，通過自動推理、全局規劃、移動控制等過程，實現機器人的自主導航移動。A*算法是一種控制性能好且發展成熟的方法，是移動機器人全局路徑規劃的常用算法之一[1]。在靜態場景中，A*算法能更快更有效地求解出最優路徑，因此被廣泛用于未知環境的全局路徑規劃，但也存在計算量大、效率低、路徑拐點不平滑等缺陷[1]。

在靜態環境下，A*算法具有最優性、完備性，但在隨著地圖數據變大搜索速度變慢。很多學者對A*算法進行許多改進，探索更高效的算法。文獻[2]通過增加h(n)的權重來提高A*算法的搜索性能；文獻[3]將柵格模型優化為無障礙、靜態障礙以及動態障礙三種移動環境下進行路徑規劃；文獻[4]提出一種動態改變步長的快速A*算法；文獻[5]提出一種基于關鍵點選取的策略來代替傳統A*算法中的Openlist和Closelist兩個列表；文獻[6]通過加入引導量對啟發函數進行改進，減少具有相同估價值的網格數量來優化算法搜索效率；文獻[7]提出了一種對啟發函數h(n)結合了分區距離信息和角度變量信息加權的改進啟發函數；文獻[8]在改進啟發函數中加入了n個父輩的信息，并根據待擴展節點和目標點相對位置選擇擴展象限；文獻[9]在啟發函數中引入當前節點的父節點啟發函數；文獻[10-11]引入了雙向搜索機制，以原始起點、終點和對向搜索所處的當前節點作為目標點進行搜索操作。

針對A*算法在大地圖中復雜障礙物環境下存在數據量大、尋路效率低、航路不平滑等問題，本文提出一種高效的改進A*算法。首先，改進A*算法的啟發函數，加入自適應的啟發信息，以提高尋路效率；然后，加入安全距離，保證了航路的安全性；最后，對原始路徑進行二次優化，進一步縮短了航路的長度并提高了航路的平滑性。

1 傳統A＊算法

1.1 地圖建模

地圖建模是路徑規劃的重要環節，目的是將實際物理環境抽象成便于計算機存儲和處理的地圖模型，實現從物理環境到虛擬地圖的映射[12-13]。在常用的地圖建模方法中，柵格地圖具有簡單有效、易于實現、便于更新的特點，是目前研究和應用最廣泛的方法。

傳統A*算法一般采用正方形柵格來進行地圖建模[14]，在正方形柵格地圖中，當前節點的鄰居節點通常為8鄰域，節點可以沿水平、豎直或對角線方向移動。如圖1所示，地圖中包含障礙物的柵格標記為障礙柵格（黑色柵格），表示不可通行的區域；地圖中不包含障礙物的柵格標記為自由柵格（白色柵格），表示可以通行的區域。

圖1 柵格地圖Fig.1 Raster map

為利用真實的海洋環境實現全局航路規劃，通過解析電子海圖提取的海洋環境信息通常由復雜幾何圖形組成，多數路徑規劃算法不能直接使用[15-16]。因此，需要采用柵格法建立基于電子海圖的海洋環境模型。首先解析電子海圖，提取其中的海域地理信息。然后利用正方形柵格網格劃分進行網格化，建立由可航行網格和不可航行網格組成的海洋環境模型。對電子海圖的海洋環境信息進行柵格化可以提高路徑規劃算法的效率[4，6-7]。

1.2 傳統A＊算法

A*算法是全局路徑規劃中一種啟發式搜索算法，在Dijkstra算法的基礎上引入了啟發式函數h(n)[3]，h(n)表示了當前節點到目標節點的估計代價。在保證了路徑最優性的同時，加入了目標節點的距離信息，提升了搜索效率。其估價函數表示為：

式中，g(n)表示累積代價，即對從初始節點到節點n的累計真實代價；h(n)表示目標代價：即節點n到目標節點的估計代價；f(n)表示估價函數，即從初始節點經過當前節點n，再到目標節點的估計代價。

1.3 算法流程

A*算法通過代價估計函數f(n)進行路徑規劃，從初始節點向附近鄰居節點進行擴展，將不超過地圖的非障礙物鄰居節點加入OpenList。然后選取OpenList中f(n)值最小的節點選為下一父節點，并將搜索過的節點加入CloseList。重復此過程直到搜索到目標節點，然后沿著父節點的方向進行回溯生成最終路徑，完成路徑規劃[2-4]。傳統A*算法的偽代碼如下所示：

A*算法在擴展鄰居節點時會把當前節點所有鄰居節點都考慮進去，該過程中會生成大量與最終路徑無關的節點，或者導致能夠通過但是花費的代價較高的情況，從而消耗大量時間，所以提高路徑規劃效率是本文的研究點之一。

2 改進A＊算法

傳統A*算法能夠對目標點進行有效的全局路徑規劃，但所規劃出的路徑存在冗余節點、轉折點多、距離障礙物過近且轉折角度過大等問題。針對這些問題，從3個方面對A*算法進行改進。一是改進估價函數加快航路搜索速度；二是加入安全距離來保證航路的安全性；三是刪除冗余節點然后使用貝塞爾曲線平滑轉折節點來減少航路轉折次數和航路長度，增加航路的平滑度。

2.1 改進啟發函數

在A*算法中，用于估計節點n的啟發代價值h(n)決定著A*算法對其他節點的擴展速度及所擴展節點是否合理。h*(n)是指節點n到目標節點的真實代價，h(n)與h*(n)的大小影響算法的精度和速度。A*算法能夠找到最短路徑的原則為h(n)的值不大于h*(n)[1]。

當h(n)=h*(n)時，A*算法可以兼顧精度和速度，是A*算法的最優狀態，但這個h(n)一般不容易找到；當h(n)＜h*(n)時，A*算法搜索效率略低，h(n)越小，意味著需要擴展的節點就越多，效率上越低，但是精度上越準確。當h(n)=0時，A*算法退化為Dijkstra算法[7]。

2.1.1 節點距離

傳統A*算法一般采用歐氏距離或曼哈頓距離來計算h(n)[9]，但是由于歐氏距離計算的h(n)很多情況下都小于柵格地圖的真實目標代價h*(n)，勢必會擴展很多不必要的節點，且往往造成所計算的距離過大或過小。為此，本文采用一種更加適合柵格地圖的距離計算方法。

對于地圖上任意兩個不同坐標節點P1(x1,y1)和P2(x2,y2)，定義x軸和y軸的絕對距離分別為：

在無障礙物環境中，柵格地圖中的兩個節點之間的移動距離都可以用圖2中兩條折線的距離相加求得。

圖2 柵格地圖節點間實際距離Fig.2 Actual distance between grid map nodes

在柵格地圖中，一般設置橫向和縱向移動一個單元的距離為1，斜向移動一個單元的距離為2。很容易得到兩個節點坐標之間的距離計算公式為：

這種距離也叫切比雪夫距離或棋盤距離。

2.1.2 目標方位信息

由A*算法具體搜索過程可知，導致其效率低的一個重要原因如圖3所示：對于無障礙物情況下，真實目標代價h*(n)確定的路徑是閉氏解，往往存在多條等價路徑，而實際上從起點到終點只需要取其中一條路徑即可。選擇f(n)值最小的點作為下一個擴展節點時，總是會出現往返搜索的情況。

圖3 閉式解路徑Fig.3 Closed-form solution path

對于這種情形，可以考慮加入目標節點的方位代價來打破對稱性，讓A*算法具有保持當前方向的傾向性，可以減少擴展沒必要的節點并平滑路徑。其次，為提高運動平穩性，在路徑規劃過程中，不僅要減小轉角，也要盡可能減少機器人轉向次數。

傳統A*算法中啟發信息h(n)只包含了當前點到目標節點的距離信息，這也導致出現多條冗余路徑，是A*算法在大地圖數據量爆炸時尋路速度變慢的原因之一。在任意節點擴展鄰居節點的時候，不僅希望路徑的長度最短，還總是希望路徑能夠傾向朝著目標節點的前進。基于此本文在啟發信息中加入當前節點到目標節點的方位信息，來引導A*算法偏向拓展分布在當前節點到目標點連線附近的節點。

取當前節點(xnode,ynode)指向目標節點(xgoal,ygoal)的引導向量a為：

如圖4所示，當前節點指向鄰居節點的向量為可行向量ti。引導向量a與可行向量ti的夾角θ可以用來表示目標節點的方位信息。夾角θ越小，說明該鄰居節點位于更靠近目標節點的方位；反之，則說明該鄰居節點位于更遠離目標節點的方位。

圖4 引導向量與可行向量的夾角Fig.4 Angle between guiding vector and feasible vector

考慮到計算方便以及cos函數在夾角取值范圍內的單調性，本文采用引導向量a與可行向量ti的夾角θ余弦值來計算方位信息，其計算公式為：

對于柵格地圖中搜索路徑的任意節點都可以分為兩種情況，前方有障礙物和前方沒有障礙物，如圖5所示。

本文根據尋路過程將節點的狀態分為前方存在障礙物和無障礙物兩個狀態。區分方法就是，從當前節點沿著引導向量的方向前方距離為dmin（一般是給定的安全距離）范圍內的節點(xi,yi)，判斷這些節點中是否存在障礙物：

式中，round表示四舍五入函數。

如圖5（a）所示，在無障礙環境中（預測節點(xi,yi)中不存在障礙物），為了加快搜索航路的速度，搜索能力偏向深度優先搜索，搜索節點的期望方向總是向著目標點的方向（紅色箭頭方向）進行，這時可以設置啟發信息為：

如圖5（b）所示，在遇到障礙物時（預測節點(xi,yi)中存在障礙物），為了加快繞開障礙物，搜索能力偏向廣度優先搜索，搜索節點時的期望方向總是向著引導向量的兩側方向（藍色箭頭方向）進行，這時可以設置啟發信息為：

圖5 柵格地圖中的兩種情況Fig.5 Two situations in grid map

可以得到柵格地圖中的自適應啟發函數為：

綜上，改進的A*算法估價函數為：

為了驗證改進啟發函數搜索路徑的快速性，使用傳統A*算法和改進A*算法進行了50次隨機實驗，在相同地圖中的起點和終點下，仿真時間對比如圖6所示。

圖6 算法時間對比Fig.6 Comparison of algorithm pathfinding time

從圖6可以看出，改進啟發函數后的算法都比傳統A*算法更快，具有更加高效的尋路速度。

2.2 安全距離

在傳統A*算法中，航路存在大量緊貼著障礙物的危險節點。若在實際航路跟蹤時，艦艇沿著障礙物邊緣行進時，安全性較差。針對這個問題，在搜索航路時需要設置一定的安全距離，迫使航路遠離障礙物。

本文提出一種保持航路與障礙物安全距離的方法。在對某個節點搜索鄰居節點時，若已經判斷該鄰居節點可以擴展，則沿著當前方向ti繼續搜索dmin（最短安全距離）步，判斷到達的節點是否為障礙物。若該節點是障礙物，則直接放棄這個鄰居節點；若不是，則將該鄰居節點加入OpenLsit。這樣可以使得航路跳過那些距離障礙物小于安全距離的節點，保證了航路的安全性。

2.3 二次航路優化

在傳統的A*算法中，路徑只進行一次規劃，得到航路是一條在A*算法模型約束條件下的最優路徑。由于在搜尋節點的過程中限制了節點的移動方向，只能向周邊八個點進行擴展搜索，使得路徑中依然存在著冗余路徑點，并且轉折次數多且很多拐點處轉向難，使艦艇行駛轉彎效率低下，不能很好地跟蹤所規劃的路徑。因此對原始航路進行二次優化，對冗余節點進行刪除，對轉折處進行平滑，獲得由起點、終點和關鍵轉折點組成的平滑航路。

2.3.1 提取路徑轉折點

A*算法得到的原始路徑存在大量的冗余節點，占據了大部分的非必要內存。因此，需要對路徑轉折點進行提取，只保留起點、終點和路徑轉折點。若原始航路在某一段路徑上保持同一個方向趨勢不變時，可以認為除了兩端之外的節點都是冗余節點。遍歷每一個航路節點，計算父節點進入它的相對方向（子節點在父節點鄰域中編號），起點的方向默認為0。

若航路是一條線段時，即在一段路徑上航路的方向保持不變并且航路長度大于閾值時，則保留這段航路的起點和終點；若航路是一條折線段時，即在一段路徑上節點的方向出現反復震蕩，則判斷震蕩的起點和終點是否能直線到達，若可以，則保留震蕩航路的起點和終點。最終獲得只包括起點、終點和轉折點的航路。

2.3.2 優選關鍵轉折點

由起點、終點和轉折點表示的航路可以大幅度減少航路的冗余節點，但還在冗余轉折點會導致航路不必要轉彎，航路的實際距離并不是最優。如圖7所示，黑色航路是在柵格地圖中規劃的最優航路；而在實際應用中，若兩節點直線可達，艦艇只需沿著紅色航線的路線便可進一步減少轉向次數和航程。因此，需要采用Dijkstra算法來刪除冗余轉折點，優選關鍵轉折點，減少航路長度和航路轉折次數。

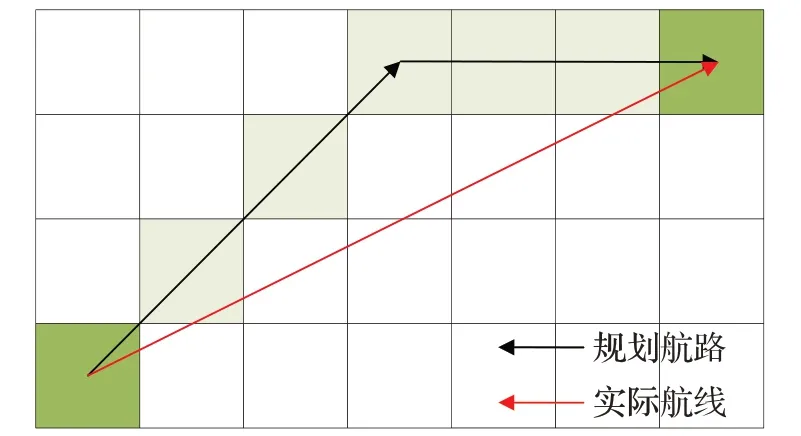
圖7 柵格地圖航路與實際航線對比Fig.7 Comparison of grid map route and actual route

Dijkstra（迪杰斯特拉）算法是典型的單源最短路徑算法，用于計算一個節點到其他所有節點的最短路徑。主要特點是以起始點為中心向外層層擴展，直到擴展到終點為止。

為了進一步優化航路，對提取的轉折點之間進行直線可達性判斷。遍歷每一個轉折節點，若兩個轉折節點之間可以直線到達，則記錄它們之間的實際距離（歐式距離）；若不是直線可達，則記錄它們的距離為無窮大。將所有可以直線互通的節點距離轉換為一個無向圖（距離矩陣）。然后使用Dijkstra算法刪除航路中不必要的轉折點，優取從起點到終點的最短路徑的關鍵轉折點。這樣進一步縮短航路長度，并減少航路的轉折次數。

2.3.3 貝塞爾曲線平滑路徑

由關鍵轉折點組成的路徑轉折次數大幅度減小，當由于轉折處都是折線，還存在且拐點處轉向難、轉彎效率低下的問題。因此，本文采用貝塞爾曲線對由關鍵轉折點進行平滑處理。

貝塞爾曲線由于操作簡單且有極強的圖像平滑能力，因此在圖形設計和路徑規劃中的應用都非常廣泛。貝塞爾曲線完全由其控制點（端點）決定其形狀，n個控制點對應著n-1階的貝塞爾曲線。通用的n階貝塞爾曲線的公式為：

式中，n是階數，t是參數，取值范圍是[0，1]。

為了保證航路在拐點處能夠平滑地轉向并且不失真，本文使用二階貝塞爾曲線對關鍵轉折點的每一個轉折處進行平滑處理。

如圖8所示，二階貝塞爾曲線需要三個端點來控制，對應航路上構成一個轉折處的三個節點P0、P1和P2。在線段P0P1和P1P2分別取兩個動點并使它們滿足如下比例關系：

圖8 二階貝塞爾曲線Fig.8 Second-order Bezier curve

然后過點P0和P2做一條與相切的拋物線，相切點為，并滿足如下比例等式：

引入參數t，令式（13）的比值為t:(1-t)，則：

當t從0變到1，即點向點P1移動、點向點P2移動時，點的移動軌跡就是由三節點P0、P1和P2三點確定的一條二階Bezier曲線，這就是式（11）的二階形式：

二次航路優化的總體效果如圖9所示，綠色節點是原始航路，藍色節點是提取的路徑轉折點，紅色節點是由Dijkstra算法篩選的關鍵轉折點，紅色路徑是使用貝塞爾曲線平滑的最終路徑。可以看到經過二次優化后的航路轉折次數大幅減少，縮短了路徑長度，提高了軌跡的平滑度，且增加了航路與障礙物之間的距離。

圖9 二次航路優化效果Fig.9 Optimization of secondary route

2.4 算法流程

改進算法在傳統A*算法的基礎首先增加的非障礙鄰居節點是否滿足安全距離判斷，篩選出大于安全距離的非障礙鄰居節點；其次增加了搜索路徑時當前節點前方有無障礙物判斷，并根據判斷結果采用對應的公式計算非障礙鄰居節點的f(n)，并記錄父節點進入當前節點的相對方向；最后，對原始航路進行二次優化，包括根據節點的父節點進入方向提取航路轉折點、判斷任意兩個航路轉折點的直線可達性生成距離矩陣，根據距離矩陣采用Dijkstra算法刪除冗余航路轉折點、對優選后的航路轉折點采用二階貝塞爾曲線進行平滑處理等操作。改進算法偽代碼如下所示：

3 仿真實驗

為了驗證本文提出的改進A*算法的航路搜索效率和航路優化效果，結合電子海圖進行仿真實驗。在硬件平臺為i5-7500，主頻3.4 GHz，運行內存8 GB的臺式機，軟件平臺為Matlab R2018b的實驗平臺上進行實驗，并與傳統A*算法進行比較。

首先，從電子海圖中獲取海洋環境信息，使用正方形柵格建立的環境模型如圖11所示，白色區域為可航行區域，黑色區域為不可航行區域。建立以水平向右為正方向的x軸，豎直向下為正方向的y軸的笛卡爾坐標系，網格數為200×87，一個網格即為一個節點。

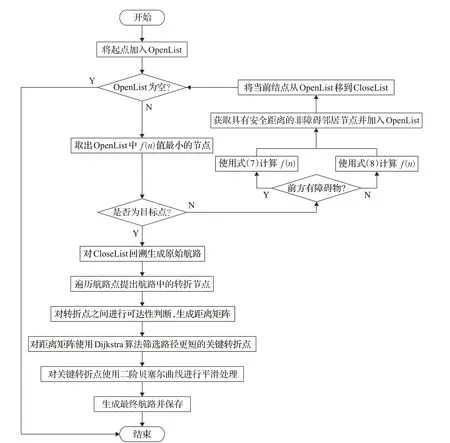
圖10 改進A*算法流程圖Fig.10 Chart of improved A*algorithm process

圖11 電子海圖柵格建模圖Fig.11 Grid modeling diagram of electronic chart

如圖12所示，是在兩組柵格化電子海圖環境模型下的航路結果對比。藍色航路為傳統A*算法規劃結果，紅色航路為改進A*算法規劃結果。

圖12 算法航路對比圖Fig.12 Comparison of route of two algorithms

從圖12（a）和表1的統計數據可以明顯看出，改進算法的航路比傳統算法的航路轉折點更少，轉彎處更加平滑，距離障礙物更遠，使得艦艇更加容易進行跟蹤。

表1 改進A*算法和傳統A*算法航路規劃結果Table 1 Comparison of traditional and improved A*algorithm

從圖12（b）和表1的統計數據可以看出，改進算法的航路比傳統算法的航路長度略長，但避開了狹窄通道，安全性更高，轉折點更少，航路更加平滑。

4 總結

針對復雜的海洋工作環境下，傳統A*算法規劃航路時出現的規劃速度慢、沿障礙物邊緣走安全性較差以及航路轉折過多且不平滑等問題，本文結合柵格化后的電子海圖環境模型，提出了一種加入目標方位信息的自適應啟發函數改進A*算法，然后刪除冗余節點后使用Dijkstra算法進一步優選航路的關鍵轉折點，最后再使用貝塞爾曲線平滑法對航路轉折處進一步優化。仿真實驗結果表明，相較于傳統A*算法，改進算法能準確地、迅速地在給定地圖中內任意兩個節點之間生成安全無碰撞且平滑全局航路，較傳統A*算法優勢明顯。