噴氣式客機層流翼氣動設(shè)計綜述
楊體浩,白俊強,段卓毅,史亞云,鄧一菊,周鑄
1. 西北工業(yè)大學(xué) 航空學(xué)院,西安 710072
2. 航空工業(yè)第一飛機設(shè)計研究院,西安 710089
3. 西安交通大學(xué) 航空航天學(xué)院,西安 710049
4. 中國空氣動力研究與發(fā)展中心,綿陽 621000
降低飛機燃油消耗率,減小環(huán)境污染是飛行器設(shè)計所追求的永恒目標(biāo)之一。發(fā)展更經(jīng)濟、更環(huán)保的“綠色航空”是未來航空工業(yè)的重要發(fā)展趨勢。層流技術(shù)的巨大減阻潛力[1-2],使其成為實現(xiàn)“綠色航空”發(fā)展目標(biāo)的核心技術(shù)之一。
典型噴氣式客機的氣動阻力主要由摩擦阻力、升致阻力、激波阻力、干擾阻力及其他附加阻力組成。摩擦阻力約占全機總阻力的50%,如圖1所示。其中摩擦阻力大約 38%來自機翼,40%左右來自機身,5%左右的摩擦阻力來自于發(fā)動機短艙[3]。層流減阻技術(shù)可在包括機翼、尾翼、翼梢小翼等升力面部件,以及短艙、機頭等非升力面部件上得到應(yīng)用,如圖2所示。研究表明,在機翼、平尾、垂尾和發(fā)動機短艙表面維系50%的層流區(qū),可使全機總阻力降低15%[3]。

圖1 典型噴氣式客機氣動阻力成份[3]

圖2 層流減阻技術(shù)在民機上的應(yīng)用范圍
世界主要航空強國及地區(qū)在過去幾十年投入了大量的人力、物力進行層流流動控制技術(shù)的研究。美國 NASA啟動了環(huán)保航空ERA (Environmentally Responsible Aviation)[4]計劃,層流控制技術(shù)是3大研究內(nèi)容之一。歐洲清潔天空聯(lián)合技術(shù)計劃(Clean Sky Joint Technology Initiative)的智能固定翼飛機(Smart Fixed Wing Aircraft, SFWA)項目和綠色支線飛機(Green Regional Aircraft, GRA)項目中,層流機翼以及具有被動/主動層流控制和載荷控制的智能機翼是重要研究內(nèi)容之一。
本文從技術(shù)原理、設(shè)計方法及設(shè)計理論對噴氣式客機的層流翼氣動設(shè)計原理進行系統(tǒng)的闡述。
1 適用于噴氣式客機的層流減阻技術(shù)
本節(jié)從典型噴氣式民機流動物理特征出發(fā),論述客機機翼上存在的典型轉(zhuǎn)捩機制,討論不同層流減阻控制技術(shù)的基本原理、優(yōu)缺點及適用范圍。
1.1 典型噴氣式客機的流動物理特征與轉(zhuǎn)捩機制
現(xiàn)役噴氣式客機為采用大涵道比渦扇發(fā)動機的翼吊/尾吊布局形式。噴氣式客機典型經(jīng)濟巡航速度一般在馬赫數(shù)0.7~0.85的高亞聲速范圍、機翼前緣后掠角在10°~38°之間。圖3 給出了運營中的典型公務(wù)機、支線客機以及干線客機的平面布局對比。除了如Hondajet這類巡航速度在馬赫數(shù)0.7左右的公務(wù)機具有小機翼前緣后掠角外,經(jīng)濟巡航速度在馬赫數(shù)0.75以上的客機均具有中等大小的機翼前緣后掠角。可見,典型噴氣式客機往往具有較大的機翼前緣后掠角,巡航狀態(tài)具有跨聲速和高雷諾數(shù)的流動特征。
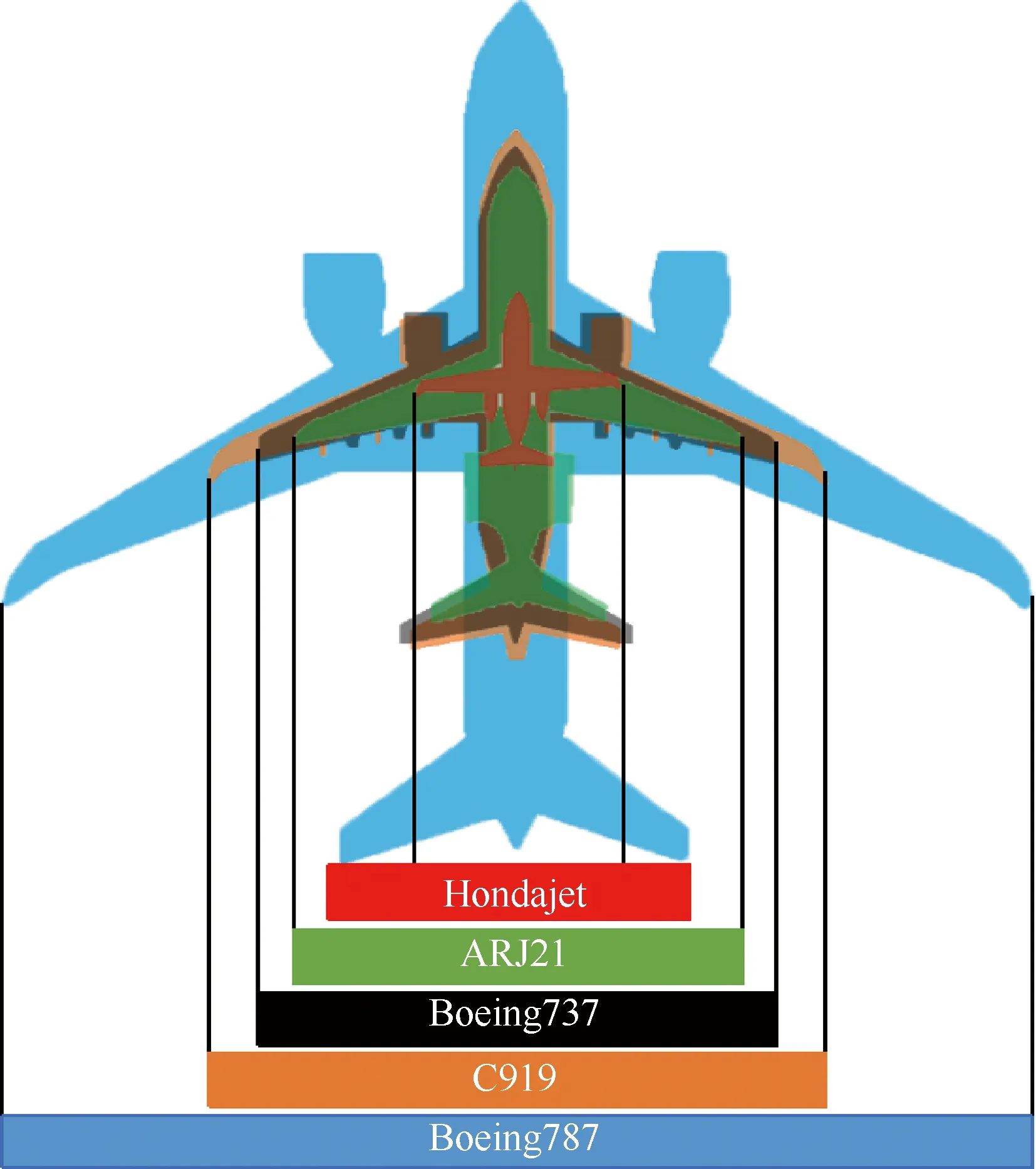
圖3 典型噴氣式客機平面參數(shù)對比
噴氣式客機具有的流動特征導(dǎo)致機翼表面存在多種轉(zhuǎn)捩機制并存的復(fù)雜流動現(xiàn)象。圖4匯總了超臨界機翼表面存在的典型轉(zhuǎn)捩現(xiàn)象[2,5-6]。受機身湍流附面層流動的影響,機翼翼根前緣可能出現(xiàn)附著線轉(zhuǎn)捩。遠離翼身結(jié)合處,超臨界機翼較大的后掠角,使得翼面上同時存在Tollmien-Schlichting (TS)波以及Crossflow(CF)渦失穩(wěn)觸發(fā)轉(zhuǎn)捩的現(xiàn)象。超臨界機翼具有的沿展向方向當(dāng)?shù)乩字Z數(shù)逐漸減小的變化趨勢,以及壓力分布形態(tài)漸變特征,使得中內(nèi)翼以及外翼段的轉(zhuǎn)捩現(xiàn)象通常分別由CF渦和TS波的穩(wěn)定性主導(dǎo)。此外,機翼表面還存在由于加工制造及昆蟲尸體污染等因素造成的幾何缺陷。這些幾何缺陷可能引起“旁路”(Bypass)轉(zhuǎn)捩現(xiàn)象[7]。
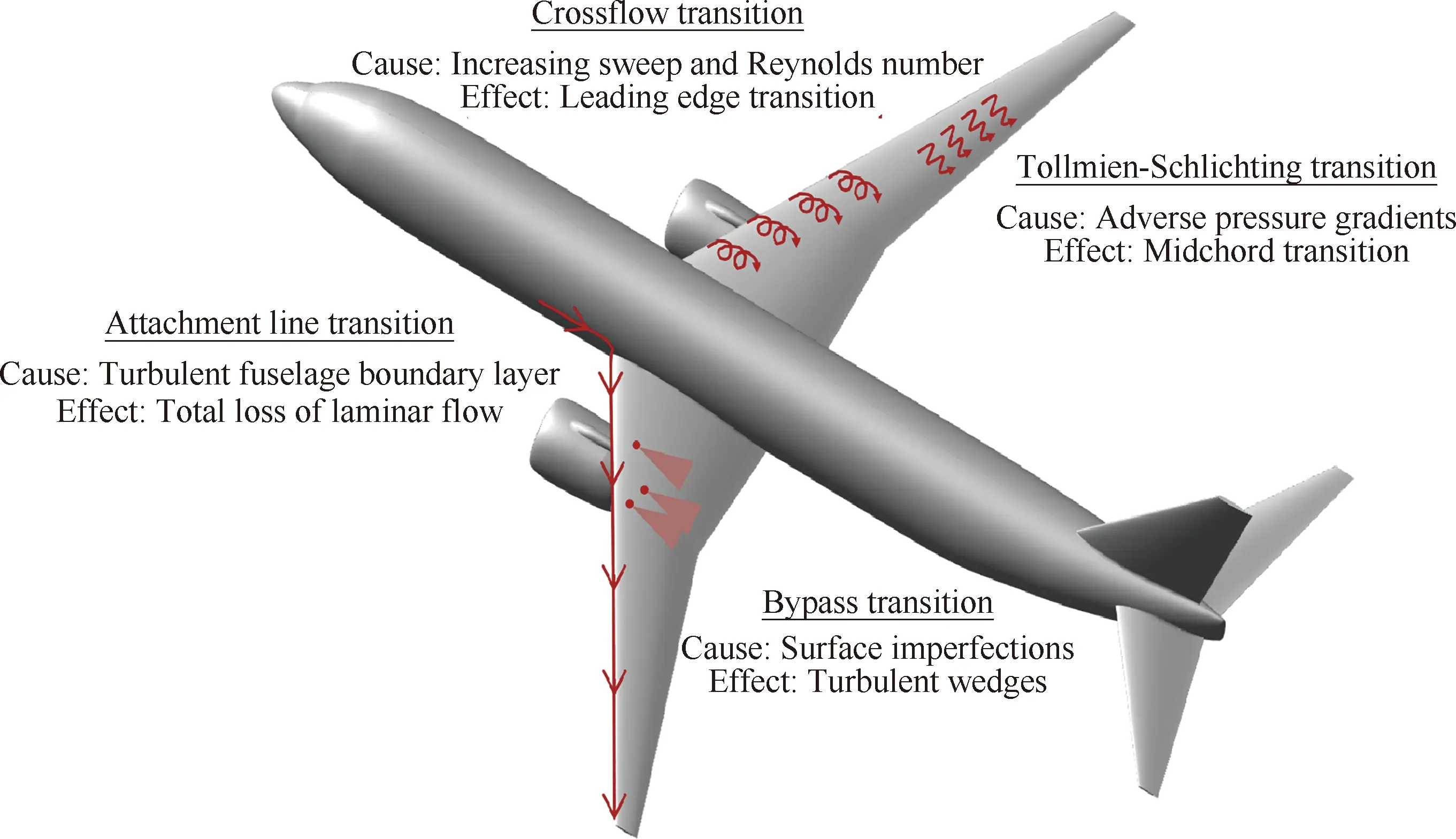
圖4 噴氣式客機超臨界機翼典型轉(zhuǎn)捩機制[2,5-6]
目前,自然層流(Natural Laminar Flow, NLF)以及混合層流控制(Hybrid Laminar Flow Control, HLFC)技術(shù)是適用于噴氣式客機的兩種最為有效的層流減阻技術(shù)[8]。但是,噴氣式客機具有的復(fù)雜轉(zhuǎn)捩現(xiàn)象,顯著增大了層流減阻技術(shù)的應(yīng)用難度。觸發(fā)不同轉(zhuǎn)捩現(xiàn)象的失穩(wěn)機制決定了NLF以及HLFC技術(shù)的適用范圍受機翼后掠角及雷諾數(shù)大小影響顯著。
圖5統(tǒng)計了不同條件下主導(dǎo)層流-湍流轉(zhuǎn)捩的失穩(wěn)機制及NLF、HLFC的有利適用范圍。小型公務(wù)機可直接采用NLF技術(shù),而現(xiàn)役的諸如B787、A350這類遠程寬體客機需要采用HLFC技術(shù)。對于B737和A320這類中短程客機,相比NLF機翼技術(shù),HLFC機翼技術(shù)在維持大范圍魯棒層流區(qū)的效能上更具優(yōu)勢。但是,倘若適當(dāng)減小機翼前緣后掠角,或者降低飛行雷諾數(shù),NLF機翼無需借助復(fù)雜吸氣控制系統(tǒng)維持魯棒層流的特點,使得NLF機翼具有比HLFC機翼更強的技術(shù)吸引力。為了充分發(fā)揮NLF機翼的技術(shù)優(yōu)勢,涌現(xiàn)了很多采用新布局形式的噴氣式客機設(shè)計構(gòu)想,如D8[9]和支撐翼[10]這兩種具有更小機翼前緣后掠角和飛行雷諾數(shù)的噴氣式客機布局形式。

圖5 層流-湍流轉(zhuǎn)捩主導(dǎo)機制及NLF、HLFC使用范圍統(tǒng)計圖
1.2 自然層流減阻技術(shù)
層流-湍流轉(zhuǎn)捩過程可視為層流邊界層在外界擾動下的穩(wěn)定性問題。四階微分方程Orr-Sommerfeld方程[11]以特征值問題的形式刻畫層流邊界層中小擾動沿流向的線性放大階段。對于不可壓流動Orr-Sommerfeld方程為
(1)
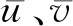
層流流動控制技術(shù)抑制擾動波發(fā)展的基本原理可通過壁面附近層流邊界層動量方程中各項的物理意義體現(xiàn)。對于二維不可壓流動,壁面附近流向方向的動量方程可寫成如下形式[13]:
(2)
式中:μw表示壁面黏性系數(shù);x為流向坐標(biāo);p為壓力;ρ為密度;T為溫度;ωw表示垂直物面的吸氣速度。當(dāng)不出現(xiàn)分離流動時,(?u/?z)w>0。顯然,為了抑制TS波的發(fā)展,維持邊界層流動的穩(wěn)定性,需要方程(2)右端項為負值,并且負值越大越好。
NLF減阻技術(shù)通過形面設(shè)計維持較大的順壓梯度dp/dx<0來有效抑制TS波的發(fā)展。但是,與抑制TS波相反,順壓梯度會促使CF渦快速失穩(wěn),需憑借逆壓梯度抑制CF渦的發(fā)展。對于前緣附著線轉(zhuǎn)捩,給定機翼后掠角,NLF機翼可通過控制翼剖面前緣半徑使附著線動量厚度雷諾數(shù)小于給定臨界值來抑制轉(zhuǎn)捩。總之,NLF技術(shù)通過合理的形面設(shè)計,維持有利的壓力分布形態(tài)特征推遲轉(zhuǎn)捩、維持可觀的層流區(qū),同時有效權(quán)衡激波阻力、誘導(dǎo)阻力等阻力成份,獲得可觀的減阻收益。
1.3 混合層流減阻技術(shù)
方程(2)表明,采用物面吸氣控制(即ωw<0)有利于維持邊界層流動的穩(wěn)定性。HLFC技術(shù)在機翼前緣附近進行吸氣控制,抑制機翼前緣附近區(qū)域TS波、CF渦的發(fā)展,以及附著線轉(zhuǎn)捩,圖6給出了NLF和HLFC工作原理對比示意圖[14]。

圖6 NLF和HLFC工作原理對比示意圖[14]
HLFC技術(shù)可視為NLF與LFC(Laminar Flow Control)技術(shù)的結(jié)合。但是與LFC不同的是,HLFC技術(shù)并不在整個翼面上,而僅僅在前梁以前區(qū)域進行吸氣控制。在非吸氣控制區(qū)域通過形面設(shè)計維持有利的壓力分布特征,抑制擾動波的發(fā)展。HLFC技術(shù)不會破壞現(xiàn)有機翼的翼盒結(jié)構(gòu),同時可極大減小需用吸氣體積流量。因此,HLFC技術(shù)是目前最具工程實踐性的主動層流控制技術(shù)之一。
HLFC 技術(shù)的工作原理決定了整個控制系統(tǒng)由理想的氣動外形、透氣吸氣壁板以及吸氣輔助系統(tǒng)組成(包括管道、吸氣泵等),如圖7所示[14]。雖然HLFC技術(shù)是從氣動學(xué)科提出的層流流動控制概念,但是其實現(xiàn)過程呈現(xiàn)出明顯的多學(xué)科屬性,涵蓋氣動、結(jié)構(gòu)、系統(tǒng)等學(xué)科。衡量HLFC技術(shù)的效益,需將氣動減阻收益同吸氣控制功率消耗代價、吸氣控制系統(tǒng)的重量懲罰進行綜合考慮。

圖7 HLFC機翼吸氣控制系統(tǒng)[14]
圖8和圖9分別面向中短程客機(如B737、A320等)和遠程客機(如A340等),借助總體估算方法給出了相比全湍流設(shè)計,采用HLFC技術(shù)后的航程增加量ΔR(圖中紅色圓點所示),以及從敏度分析角度顯示了氣動減阻收益(巡航升阻比K的提高)、功率消耗Ppump代價及吸氣控制系統(tǒng)重量WHLFC懲罰變化對HLFC綜合收益的影響規(guī)律。航程估算采用布雷蓋航程公式。參數(shù)敏度分析結(jié)果顯示,一定范圍內(nèi),相比吸氣功耗及控制系統(tǒng)重量懲罰,氣動減阻大小對HFLC綜合收益影響更為顯著。此外,對于主要在巡航段使用的HLFC技術(shù),由于遠程客機巡航段在整個任務(wù)剖面中占有更大比重,因此該技術(shù)在遠程客機上具有更大的綜合收益。
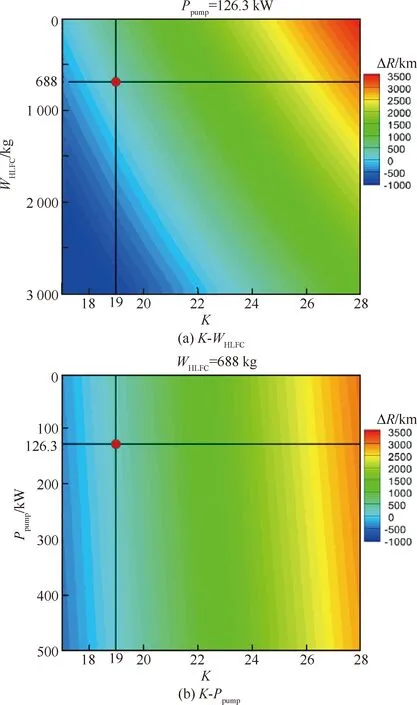
圖8 面向中短程客機的HLFC機翼綜合收益參數(shù)分析

圖9 面向遠程客機的HLFC機翼綜合收益參數(shù)分析
德國宇航中心(DLR)利用給定航段內(nèi)燃油消耗減少引起的燃油費的降低,量化HLFC技術(shù)的綜合收益,并給出了敏度分析結(jié)果,如表1所示[15]。研究結(jié)果顯示,對于預(yù)計年飛行500個周期的客機而言,氣動阻力CD降低1%,每年可節(jié)省燃油費約19萬美元。相比之下,吸氣功耗或者吸氣控制系統(tǒng)重量降低1%,每年節(jié)省的燃油費不超過1 800美元。

表1 基于燃油花費成本的HLFC機翼收益及敏度分析[15]
雖然HLFC技術(shù)工程實現(xiàn)過程呈現(xiàn)明顯的多學(xué)科屬性,但是從最大化綜合收益角度出發(fā),以較小的吸氣功耗和系統(tǒng)重量懲罰代價,顯著提高氣動效率是HLFC技術(shù)發(fā)展的重要趨勢。
2 面向噴氣式客機的層流減阻技術(shù)發(fā)展概述
本節(jié)總結(jié)了國、內(nèi)外面向噴氣式客機的NLF和HLFC減阻技術(shù)的發(fā)展。
2.1 國外發(fā)展情況
美國NACA(National Advisory Committee for Aeronautics)在20世紀(jì)30年代就對自然層流翼型進行了大量研究,設(shè)計、發(fā)展了“NACA 6”系列及“NACA 7”系列的自然層流翼型[16]。最早有關(guān)層流流動控制LFC的風(fēng)洞試驗研究是在20世紀(jì)30—40年代期間開展的[17-18]。NACA 工程師提出了基于多吸氣縫道概念的層流流動控制技術(shù),為后續(xù)混合層流控制概念的提出奠定了基礎(chǔ)。這一時期針對NLF和LFC技術(shù)的探索在一定程度上提升了當(dāng)時人們對邊界層內(nèi)轉(zhuǎn)捩過程的理解。
20世紀(jì)70年代石油危機的爆發(fā),使得80—90年代期間層流流動控制技術(shù)得到航空工業(yè)界的廣泛關(guān)注,相關(guān)風(fēng)洞、飛行試驗研究不斷涌現(xiàn),并且主動層流流動控制開始轉(zhuǎn)向效率更高的HLFC概念。圖10為國際上面向噴氣式客機的NLF/HLFC技術(shù)發(fā)展的主要歷程。

圖10 國外面向噴氣式客機的NLF/HLFC技術(shù)發(fā)展
美國NASA先后改裝F-111/TACT以及F-14變后掠飛機,進行了一系列變后掠角NLF機翼飛行試驗,評估橫流對轉(zhuǎn)捩的影響,極大地提升了研究者們在機翼后掠角和剖面翼型對層流轉(zhuǎn)捩耦合影響方面的認(rèn)知[19]。波音公司在B757機翼上添加了具有21°后掠角的NLF翼套[20],初步探究了大涵道比翼吊發(fā)動機噪聲擾動對層流邊界層穩(wěn)定性的影響。飛行試驗表明,發(fā)動機噪聲擾動對橫流穩(wěn)定性的影響相對較小。
NASA啟動了EETT(Energy Efficient Transport Technology) 項目,開展了大量數(shù)值和風(fēng)洞試驗研究,促使其在HLFC技術(shù)方面取得巨大研究進展[18,21-22]。NASA在Jetstar飛機上改裝HLFC翼套開展飛行試驗,成功驗證了飛行條件下防昆蟲污染、除冰及吸氣控制系統(tǒng)運行的有效性。進一步,波音公司基于B757開展了HLFC翼套飛行試驗研究[23],初步形成了飛行試驗數(shù)據(jù)庫。高雷諾數(shù)飛行條件下HFLC機翼翼套最大實現(xiàn)了65%弦長的層流區(qū)。GE (General Electric)公司與NASA合作推進了HLFC短艙概念的氣動設(shè)計和飛行試驗[23]。其表面可魯棒地實現(xiàn)40%以上短艙長度的層流范圍。相關(guān)數(shù)值、風(fēng)洞及飛行試驗研究成果顯著增強了航空工業(yè)對HLFC技術(shù)應(yīng)用潛力的信心。
同一時期,歐洲圍繞NLF/HLFC技術(shù)也開展了大量研究。法國和德國分別以Falcon-50和ATTAS飛機為試驗平臺,開展大量飛行試驗[24]。歐盟在F100飛機機翼上加裝NLF翼套,以飛行試驗方式在綜合考慮加工制造工藝、實際運營和使用維護影響,研究NLF超臨界機翼在小型公務(wù)機上工程實現(xiàn)的可行性[25-26]。Dassault公司與法宇航在Falcon-900飛機內(nèi)翼段安裝HLFC系統(tǒng),測試HLFC系統(tǒng)在真實飛行環(huán)境下的可靠性[27]。隨后,Airbus與德宇航、法宇航合作,開展HLFC垂尾研究,推進了A320 HLFC垂尾飛行試驗[28]。
進入21世紀(jì),隨著對層流流動控制技術(shù)研究的不斷深入,圍繞NLF/HLFC技術(shù)的研究開始推進工程應(yīng)用轉(zhuǎn)化,部分技術(shù)甚至已經(jīng)得到實際應(yīng)用。Piaggio P-180和Hondajet小型公務(wù)機[29]氣動設(shè)計采用了NLF機身和NLF機翼技術(shù),顯著降低了燃油消耗率。B787-8采用了NLF短艙氣動設(shè)計技術(shù)[30]。波音公司將NLF小翼概念應(yīng)用在B737 Max的小翼上[30]。
由于大型客機的流動現(xiàn)象復(fù)雜、存在多種轉(zhuǎn)捩機制,使得層流流動控制技術(shù)還未在超臨界機翼上得到工程應(yīng)用。但是,相關(guān)研究仍在不斷推進。意大利Piaggio航空公司設(shè)計了具有20°前緣后掠角的NLF超臨界機翼UW-5006[31]。設(shè)計馬赫數(shù)0.78,最大雷諾數(shù)10.0×106。風(fēng)洞試驗顯示,典型巡航工況下可維持40%弦長以上的層流區(qū)。空客公司將A340約1/3展長的外翼替換成前緣后掠角更小的NLF超臨界機翼試驗段,并開展飛行試驗[32]。該試驗段的設(shè)計將NLF超臨界機翼的氣動外形設(shè)計與標(biāo)準(zhǔn)的機翼結(jié)構(gòu)設(shè)計進行了結(jié)合。NASA在CRM (Common Research Model) 基礎(chǔ)上發(fā)展了NLF超臨界機翼標(biāo)模CRM-NLF[33]。機翼前緣后掠角35°,巡航馬赫數(shù)0.85。風(fēng)洞試驗結(jié)果顯示,在雷諾數(shù)15.0×106條件下,整個翼面上仍能維持可觀的層流區(qū)。
歐盟圍繞HLFC技術(shù),特別是HLFC垂尾啟動了一系列研究計劃,持續(xù)開展了大量風(fēng)洞及飛行試驗研究[34]。這一階段研究旨在通過簡化吸氣控制系統(tǒng),突破翼面防污染、除冰技術(shù),闡明加工制造帶來的表面缺陷的影響,發(fā)展高效、可靠的數(shù)值模擬和設(shè)計工具等,借此提高HLFC機翼、HLFC短艙及HLFC垂尾技術(shù)的技術(shù)成熟度。波音公司計劃在B787-9尾翼上測試HLFC垂尾[30]。
2.2 國內(nèi)發(fā)展情況
相比歐美地區(qū),國內(nèi)在NLF及HLFC減阻技術(shù)領(lǐng)域內(nèi)的研究起步較晚。圖11為20世紀(jì)90年代后中國面向噴氣式客機的NLF/HLFC技術(shù)發(fā)展的主要歷程。
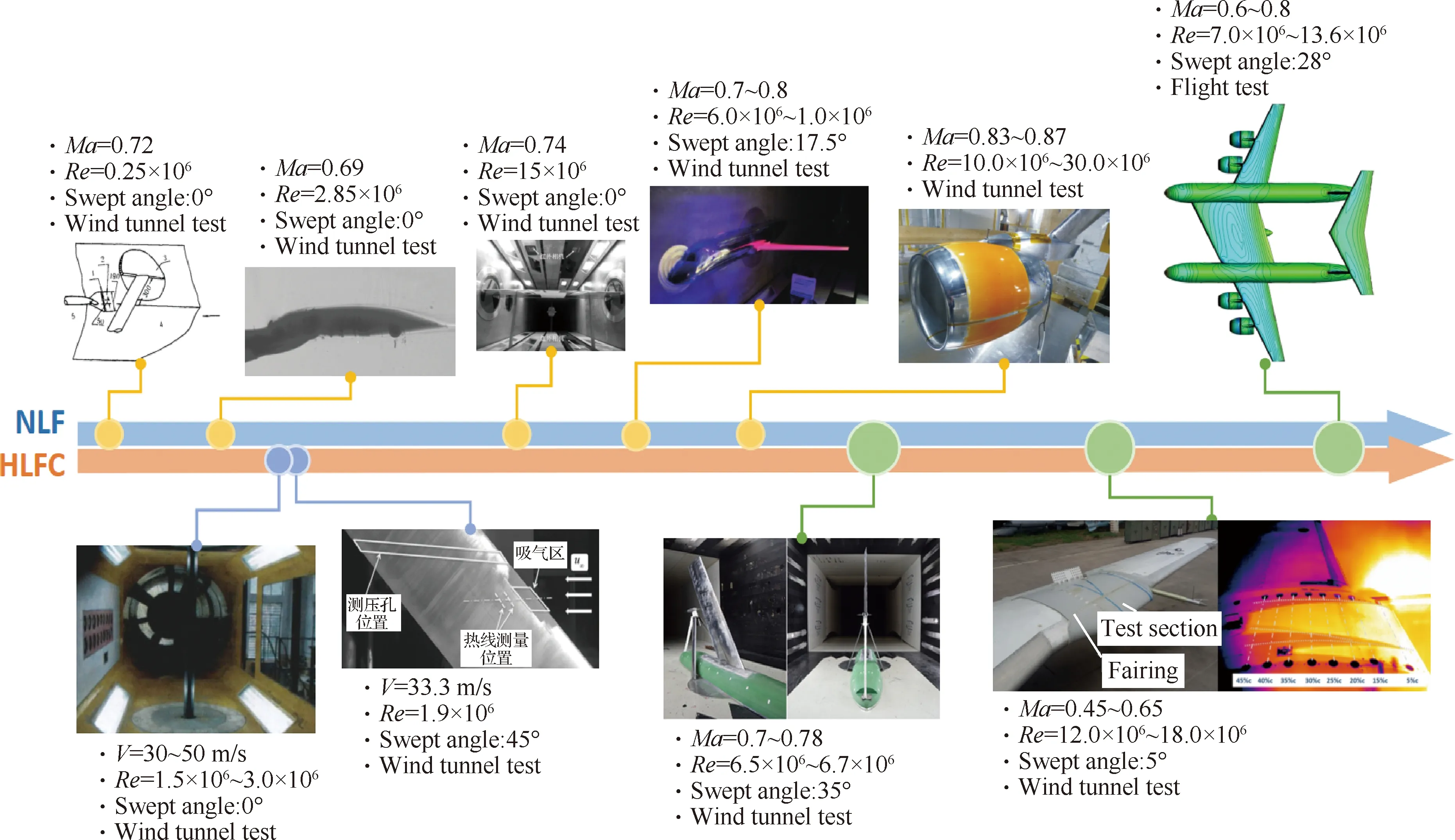
圖11 國內(nèi)面向噴氣式客機的NLF/HLFC技術(shù)發(fā)展
該技術(shù)發(fā)展早期,國內(nèi)主要基于國際上的標(biāo)準(zhǔn)模型進行風(fēng)洞試驗研究,或者基于公開翼型開展補充性的風(fēng)洞試驗。試驗內(nèi)容集中于NLF翼型/機翼氣動特性及轉(zhuǎn)捩預(yù)測研究。20世紀(jì)90年代,國內(nèi)科研工作者開始自主設(shè)計層流超臨界翼型/機翼,并開展了一系列風(fēng)洞實驗。喬志德等[35-36]設(shè)計了NPU-L72513超臨界NLF翼型,在Ma=0.72、Re=0.25×106的風(fēng)洞試驗條件下可維持40%弦長以上的層流區(qū)。進一步設(shè)計了巡航馬赫數(shù)Ma=0.69的高亞聲速NLF翼型,風(fēng)洞試驗結(jié)果顯示設(shè)計點附近可維持50%弦長以上層流段[37]。但是這一階段的研究主要面向二維翼型,并且風(fēng)洞試驗雷諾數(shù)較低,不超過3.0×106。進入2010年,相關(guān)研究開始向高雷諾數(shù)、復(fù)雜構(gòu)型發(fā)展。中國商飛[38]采用反設(shè)計方法設(shè)計了具有較好低阻特性的高雷諾數(shù)NLF超臨界翼型,Ma=0.74、Re=15.0×106風(fēng)洞試驗條件下可維持60%弦長以上的層流范圍。進一步,開展了跨聲速NLF短艙風(fēng)洞試驗研究[39]。中航工業(yè)第一飛機設(shè)計研究院[40]基于典型支線客機翼身組合體構(gòu)型,設(shè)計了前緣后掠17.5°的超臨界NLF機翼。設(shè)計馬赫數(shù)0.75,雷諾數(shù)Re=10.0×106,可穩(wěn)定維持40%~50%弦長層流區(qū)。白俊強和史亞云等[41]基于具有35°后掠角超臨界機翼的翼身組合體構(gòu)型,采用數(shù)值與風(fēng)洞試驗相結(jié)合的方法,研究了壓力分布形態(tài)特征與TS波及CF渦失穩(wěn)觸發(fā)轉(zhuǎn)捩的影響關(guān)系。2020年前后,國內(nèi)NLF機翼技術(shù)得到進一步發(fā)展,相關(guān)研究已經(jīng)開始逐步從風(fēng)洞試驗驗證向?qū)嶋H飛行試驗驗證階段邁進。中國飛行試驗研究院采用層流翼套試驗技術(shù),開展了NLF機翼飛行試驗[42],飛行馬赫數(shù)0.45~0.65,雷諾數(shù)最高Re=18.0×106,典型工況下可穩(wěn)定維持理論設(shè)計的層流范圍,達45%弦長。中航工業(yè)第一飛機設(shè)計研究院也計劃于2022年基于無人飛行試驗平臺,開展無后掠自然層流翼飛行試驗。
HLFC減阻技術(shù)方面,2010年前后才出現(xiàn)一些圍繞HLFC技術(shù)的風(fēng)洞試驗研究的相關(guān)公開報道。但是這些早期的風(fēng)洞試驗[43-44]旨在探究HLFC技術(shù)的實現(xiàn)原理和轉(zhuǎn)捩抑制效果,存在試驗?zāi)P秃唵巍⒃囼烇L(fēng)速及雷諾數(shù)過小的不足,遠達不到噴氣式客氣典型飛行工況狀態(tài)。之后,史亞云等[45]基于具有35°后掠角超臨界機翼的翼身組合體構(gòu)型,在跨聲速試驗條件下詳細研究了HLFC吸氣控制強度、壓力分布特征、轉(zhuǎn)捩抑制效果間的定量關(guān)系,形成了數(shù)據(jù)庫。中國飛行試驗研究院[46-48]采用自主設(shè)計的混合層流翼套,在真實飛行環(huán)境下研究了HLFC技術(shù)抑制TS波失穩(wěn)誘導(dǎo)轉(zhuǎn)捩的能力。相同飛行條件下,相比NLF試驗,采用HLFC技術(shù)后轉(zhuǎn)捩位置最大推遲了30%弦長以上。中航工業(yè)第一飛機設(shè)計研究院也計劃于2022年基于具有28°前緣后掠的無人飛行試驗平臺,采用飛行試驗技術(shù)研究HLFC技術(shù)抑制CF渦失穩(wěn)誘導(dǎo)轉(zhuǎn)捩的能力。
3 層流-湍流轉(zhuǎn)捩工程預(yù)測
層流-湍流轉(zhuǎn)捩是一個及其復(fù)雜的過程,目前國內(nèi)外尚沒有一個嚴(yán)格意義上通用的轉(zhuǎn)捩模型可以準(zhǔn)確的預(yù)測航空領(lǐng)域存在的多種機制誘導(dǎo)的轉(zhuǎn)捩現(xiàn)象[2]。但是隨著計算機和CFD的發(fā)展,從針對不同轉(zhuǎn)捩機制的機理研究,到面向工程應(yīng)用的高可信度轉(zhuǎn)捩預(yù)測方法建立,在邊界層轉(zhuǎn)捩問題中得到了廣泛關(guān)注。直接數(shù)值模擬方法(Direct Numerical Simulation, DNS)可以精確的刻畫邊界層內(nèi)感受機制、擾動初始發(fā)展階段、非線性擾動相互干擾階段、湍流斑形成及最終匯集成全湍流的過程。在邊界層轉(zhuǎn)捩過程中,外部湍流擾動可能直接導(dǎo)致瞬態(tài)增長(Transient Growth)失穩(wěn)或者“旁路”轉(zhuǎn)捩,見圖12。DNS計算所需的網(wǎng)格量極大且時間步長較小。現(xiàn)階段,DNS所需要的計算資源及其計算效率無法滿足真正意義上的工程計算[49]。大渦模擬(Large Eddy Simulation, LSE)理論上對大尺度渦進行直接數(shù)值模擬求解,對小尺度渦通過模型封閉[50]。受制計算資源,LES目前只在簡單構(gòu)型及低雷諾數(shù)流動中得到應(yīng)用,并且LES的模型封閉適應(yīng)性限制其在層流-湍流轉(zhuǎn)捩中的發(fā)展。
考慮到計算精度和計算效率,基于高可信度的RANS方程在工程中得到了廣泛應(yīng)用。國內(nèi)外研發(fā)了不同的RANS求解器,如國外著名的CFL3d[51]、Overflow[52]、ADflow[53]等結(jié)構(gòu)求解器,TAU、Fun3d、SU2[54]等非結(jié)構(gòu)求解器,以及ANSYS公司開發(fā)的Fluent和CFX軟件,國內(nèi)的風(fēng)雷(PHengLEI)、HUNS3D[55]、TeAM[56]等。基于高可信度求解器,相應(yīng)的發(fā)展了多種轉(zhuǎn)捩預(yù)測方法,主要分為兩類:一類是基于穩(wěn)定性理論的轉(zhuǎn)捩預(yù)測方法;另一類是基于輸運方程的轉(zhuǎn)捩模型。
3.1 基于穩(wěn)定性理論的轉(zhuǎn)捩預(yù)測方法
穩(wěn)定性理論的基本思想是,模擬擾動的線性/非線性階段,結(jié)合eN方法及轉(zhuǎn)捩判據(jù),從而預(yù)測轉(zhuǎn)捩位置。該類方法主要包括線性穩(wěn)定性理論(Linear Stability Theory, LST)和拋物化方程(Parabolic Stability Equation, PSE)。線性穩(wěn)定性理論是基于平行流小擾動假設(shè),擾動定義為
(3)

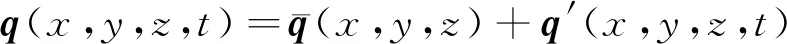
(4)
分別將式(3)和式(4)帶入Navier-Stokes方程,并結(jié)合小擾動,假設(shè)忽略二階項,最終求得特征值方程,當(dāng)為二維流動時,即為Orr-Sommerfeld方程。對于一般二維/三維、不可壓/可壓流動,基于線性穩(wěn)定性理論的特征值方程可表示為
(5)

得到擾動增長率,并不能確定具體的轉(zhuǎn)捩位置,因而引入eN方法。針對二維流動,假設(shè)某一擾動初始擾動為A0,其在下游的擾動幅值演化可表示為
(6)
可進一步表示為
(7)
式中:x0為擾動流向起始位置;x為當(dāng)?shù)財_動位置。當(dāng)N值達到對應(yīng)的轉(zhuǎn)捩閾值后,該點即為轉(zhuǎn)捩位置。轉(zhuǎn)捩閾值可由Mack公式[59]獲得,或者由基于風(fēng)洞/飛行試驗的轉(zhuǎn)捩閾值圖表決定。對于三維流動,需要進一步明確擾動傳播的方向,即積分路徑。
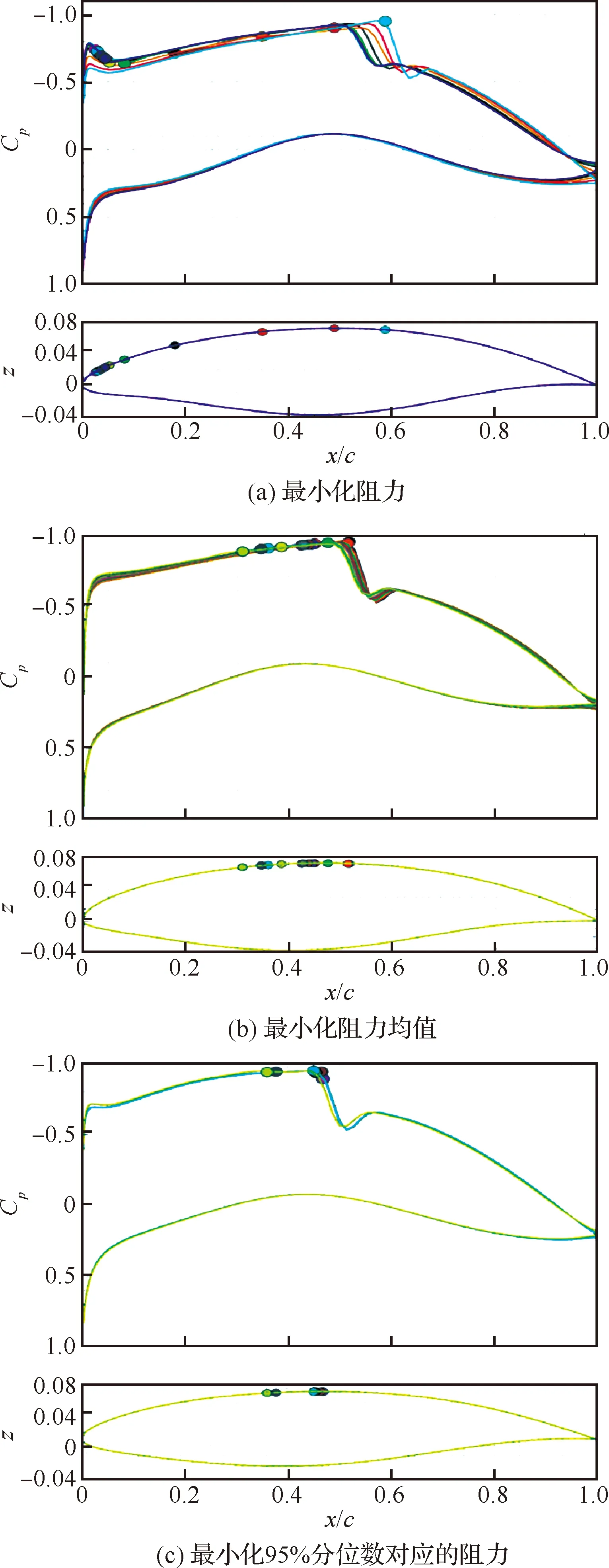
一般認(rèn)為,非平行效應(yīng)作為小量而忽略,但是由于積分效應(yīng),在實際中非平行效應(yīng)的累積效應(yīng)還是不可忽視,尤其是在非線性階段,如圖13所示[5]。基于非平行流,具有代表特征的是拋物化方程,其擾動定義為

圖13 基于LST、LPSE、NPSE的數(shù)值模擬與試驗對應(yīng)擾動放大因子對比[5]
(8)
對應(yīng)的方程可以表示為
(9)
(10)

基于線性穩(wěn)定性理論和拋物化理論的轉(zhuǎn)捩預(yù)測方法在國內(nèi)外得到了廣泛的研究與應(yīng)用。Malik等[60]基于時間模式推導(dǎo)了三維可壓縮線性穩(wěn)定方程,采用高效的Rayleigh商求解不同擾動頻率和不同擾動波長下的擾動增長率和對應(yīng)的特征向量。針對特征值搜索,分別采用了全局和當(dāng)?shù)夭呗裕瑸榱斯?jié)省計算時間和內(nèi)存空間,基于初值,采用當(dāng)?shù)鼗蠼狻alik[61]還針對高超聲速穩(wěn)定性問題進行了數(shù)值求解研究,分別通過二階有限差分方法、四階緊致差分格式以及Chebyshev譜離散控制方法,研究了馬赫數(shù)10以內(nèi)的方程求解。Schrauf[25]進一步發(fā)展了基于時間模式的線性穩(wěn)定理論,并廣泛的應(yīng)用在算例及試驗分析中。Arnal[62]、Chen和Cebeci[63]推導(dǎo)了空間模式的線性穩(wěn)定理論方程。Cebeci和Stewarton[64]從復(fù)變函數(shù)的角度,研究了一個波包的演化,即通過鞍點法(?α/?β=0)確定展向波數(shù),從而確定擾動波傳播的群速度方向。
國內(nèi)蘇彩虹[65]采用數(shù)值模擬對鞍點法的物理機制進行了闡述(圖14),即鞍點法確定的擾動傳播方向是波包(Wave packet)波峰的演化方向。蘇彩虹[65]對于線性穩(wěn)定性理論在高超聲速轉(zhuǎn)捩預(yù)測中遇到的問題進行了探討,強調(diào)了在使用線性穩(wěn)定理論預(yù)測高超聲速轉(zhuǎn)捩時考慮感受性的重要性。
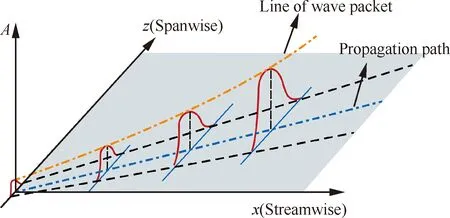
圖14 鞍點法積分策略的物理含義[65]
為了考慮非平行流效應(yīng),國內(nèi)外還開展了拋物化理論的研究。Herbert等[66]分別求解了不可壓縮拋物化理論和可壓縮拋物化方程,并與DNS數(shù)值模擬結(jié)果進行了對比,結(jié)果顯示拋物化理論可以較好的捕捉非線性階段擾動及非平行流效應(yīng)。Schrauf[25]針對ATTAS飛行試驗應(yīng)用了非拋物化理論進行研究,相比線性穩(wěn)定理論,拋物理論得到的橫流渦擾動值更大,同時觀察到TS和CF渦之間的相互干擾。國內(nèi)劉一方[67]通過拋物化理論研究了超聲速平板邊界層的擾動演化過程。趙磊[68]改進了拋物化方程的求解算法,且研究了不同狀態(tài)下橫流駐渦的演化過程。徐國亮等[69]基于非線性拋物化理論分析了馬赫數(shù)0.1~2.0的橫流失穩(wěn)機制,并拓展到后掠翼,分別給出了曲率、雷諾數(shù)及后掠角對橫流二次失穩(wěn)的影響。基于拋物化理論的轉(zhuǎn)捩預(yù)測使得邊界層轉(zhuǎn)捩演化過程得到了充分的認(rèn)識,但是拋物化理論計算效率低,同時面臨求解復(fù)雜的問題。同時較為簡單的線性拋物化方程相比線性穩(wěn)定理論,在線性階段差異較小,但付出了高昂的計算代價。因而,目前航空領(lǐng)域的高雷諾數(shù)主要還是應(yīng)用線性穩(wěn)定性理論或者改進的線性穩(wěn)定性理論。
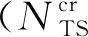
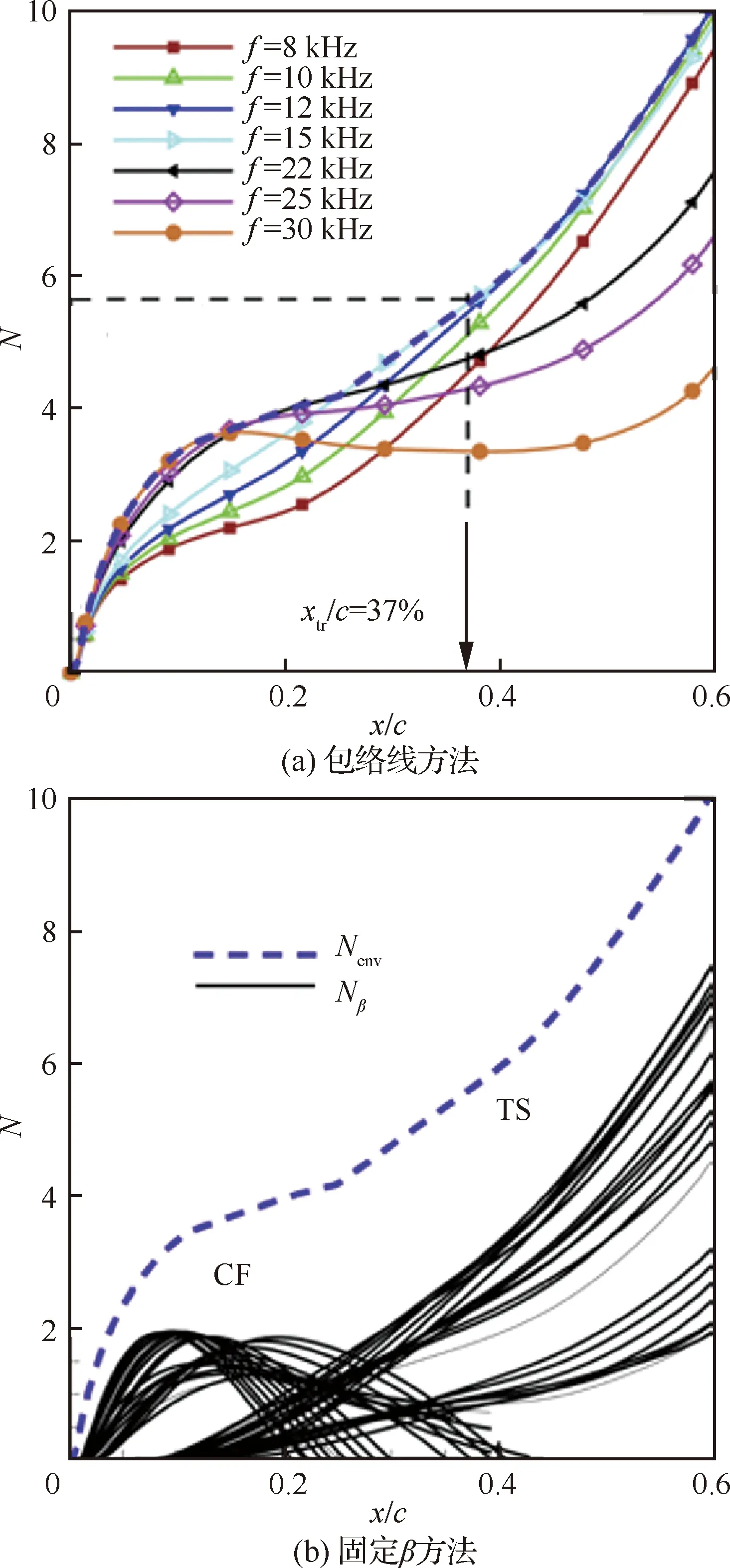
圖15 不同積分策略給出的擾動因子增長圖對比[2]
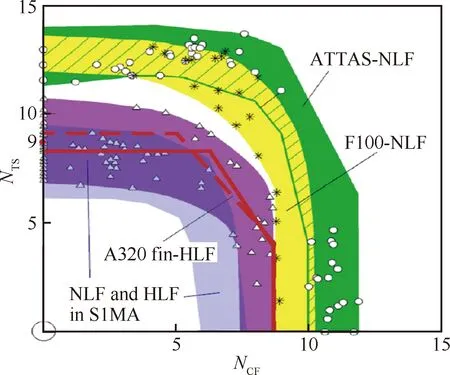
圖16 臨界N因子值圖[41,70]
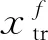

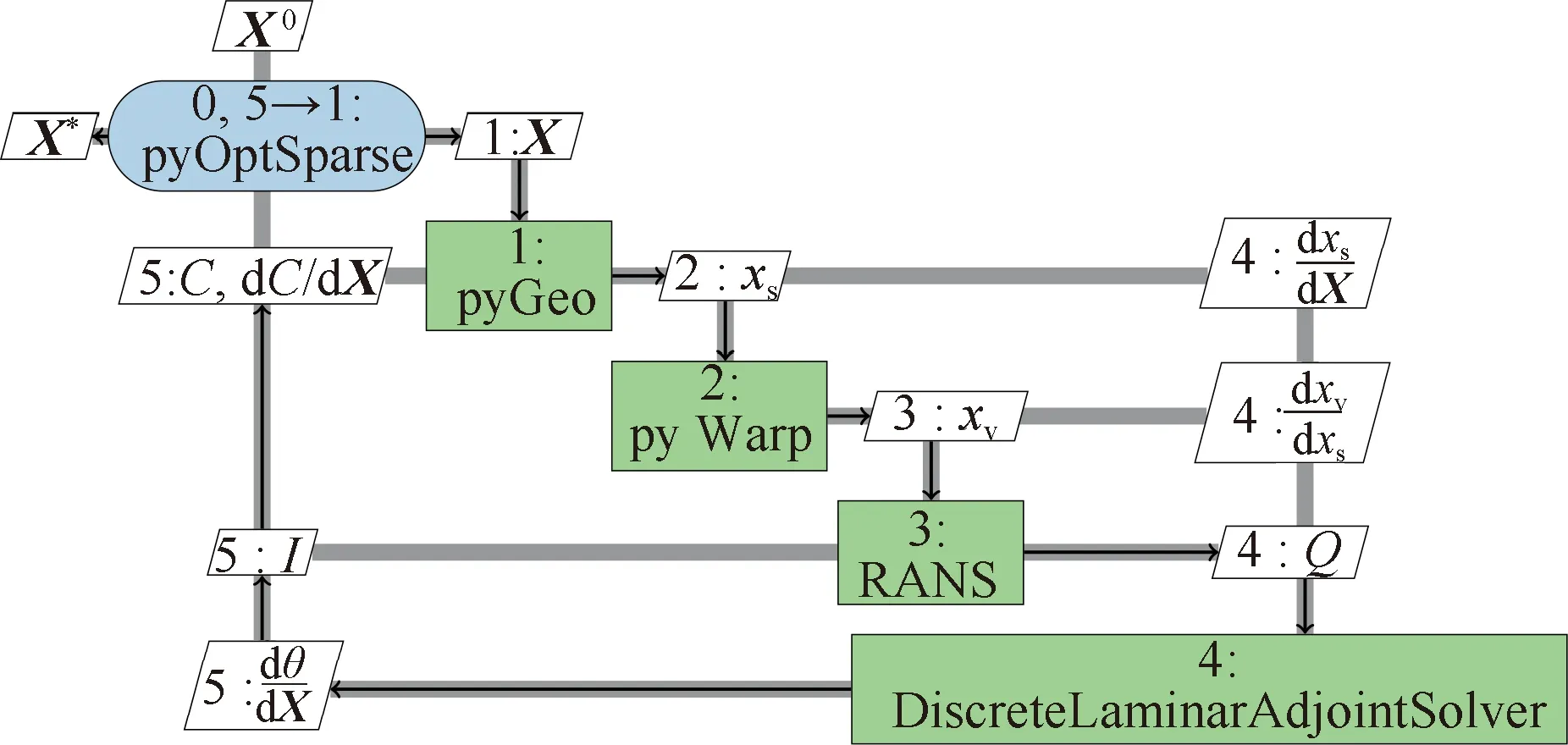
圖17 基于穩(wěn)定性理論的eN方法耦合RANS迭代計算示意圖[71-73]
針對耦合RANS求解器,邊界層信息的計算主要有兩種方式:一種是求解層流邊界層方程;另一種是直接提取RANS方程對應(yīng)的流場解。一般層流邊界層方程是基于錐形流假設(shè)得到的,從而使得該方法適用于展弦比較大的構(gòu)型,且該方法計算效率高,因而廣泛地應(yīng)用在機翼的邊界層信息計算中。而對于三維流動較強的構(gòu)型,提取RANS求解的流場更為合適,該方法要求有足夠的網(wǎng)格密度,尤其是在法向靠近物面的區(qū)域。為了進一步提高計算效率,Arnal[74]和Cliquet[75]等提出了基于線性穩(wěn)定理論的數(shù)據(jù)庫方法,即通過穩(wěn)定性分析及相關(guān)試驗,建立擾動增長率σ、σI、σV與位移厚度雷諾數(shù)Reδ的關(guān)系(圖18)。相比求解線性穩(wěn)定方程,該方法在保證工程使用精度的情況下具有明顯的計算效率優(yōu)勢。

圖18 擾動放大率與位移厚度雷諾數(shù)關(guān)系示意圖[72]
根據(jù)邊界層信息求解和擾動增長率計算的方式,轉(zhuǎn)捩計算與RANS的耦合有不同的組合:包括不同邊界層信息求解(求解層流邊界層方程/直接提取RANS流場邊界層信息)和不同擾動放大因子計算(穩(wěn)定性理論/數(shù)據(jù)庫)。DLR[76]基于非結(jié)構(gòu)求解器實現(xiàn)了不同組合的轉(zhuǎn)捩預(yù)測方法,并對二維翼型、三維機翼及復(fù)雜增升裝置構(gòu)型進行了轉(zhuǎn)捩預(yù)測驗證。Liao等[77]基于非結(jié)構(gòu)求解器Fun3d研究了基于流場邊界層提取和線性穩(wěn)定理論的轉(zhuǎn)捩預(yù)測方法,結(jié)果表明,在物面附近網(wǎng)格具有足夠精度時,得到的計算結(jié)果與試驗或者邊界層求解吻合。Shi等[72,78]基于離散伴隨結(jié)構(gòu)求解器ADflow分別研究了基于線性穩(wěn)定理論和基于數(shù)據(jù)庫的轉(zhuǎn)捩預(yù)測,基于數(shù)據(jù)庫的快速求解有利于高效求解考慮轉(zhuǎn)捩的耦合伴隨方程。國外基于eN方法進行了層流翼設(shè)計研究,包括Telfona前掠翼[70]、UW5006[31]、CRM-NLF[79]、翼套飛行試驗[80]等。國內(nèi)的楊體浩[81]、楊一雄[56]等將基于eN方法轉(zhuǎn)捩預(yù)測應(yīng)用在自然層流和混合層流的設(shè)計中,進行了自然層流、混合層流的風(fēng)洞模型及翼套模型的設(shè)計。韓忠華等[82]基于該方法結(jié)合代理模型對后掠翼進行了單點和多點優(yōu)化設(shè)計。大量研究和試驗表明基于eN方法在工程應(yīng)用中是可靠的。
3.2 基于輸運方程的轉(zhuǎn)捩模型


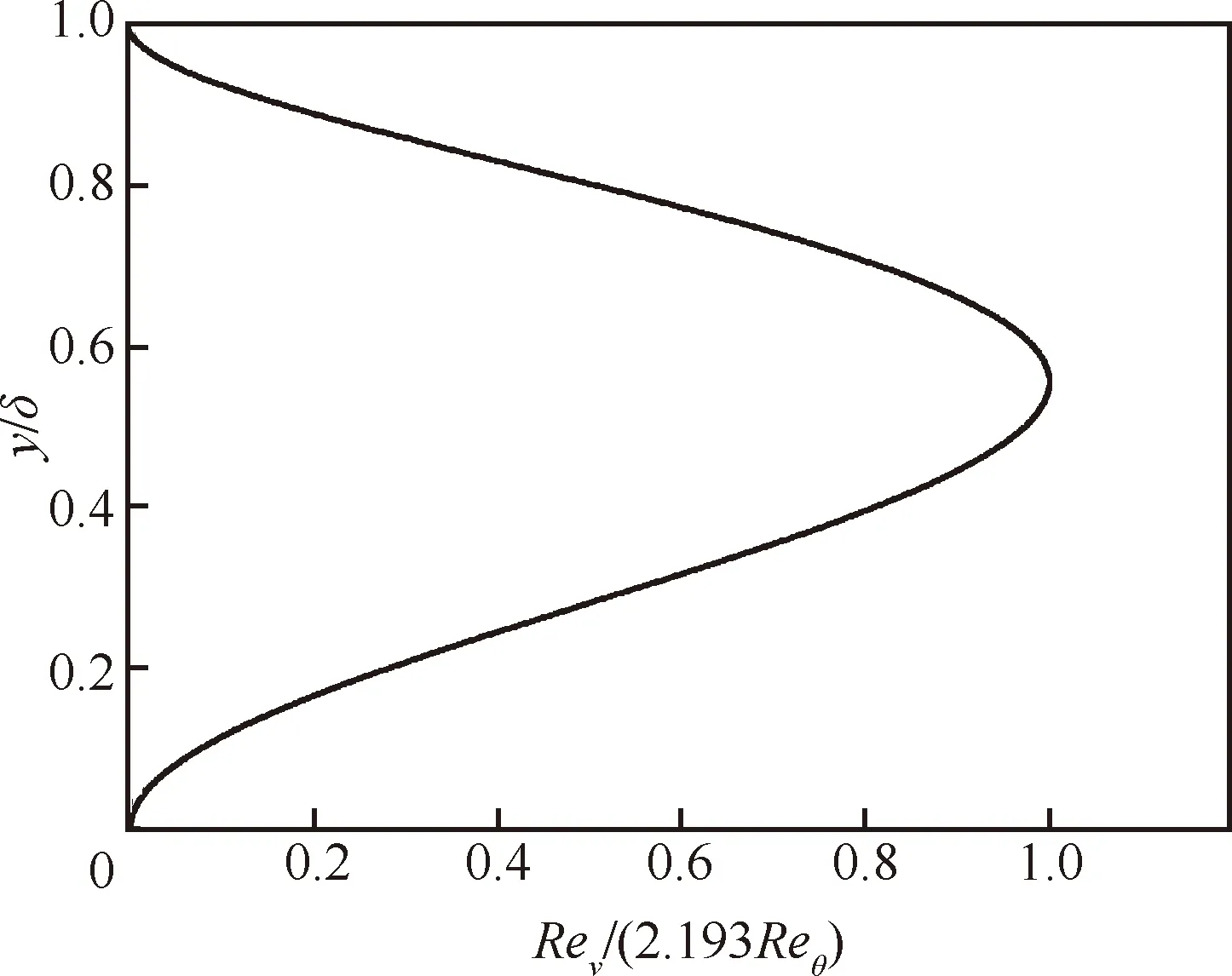
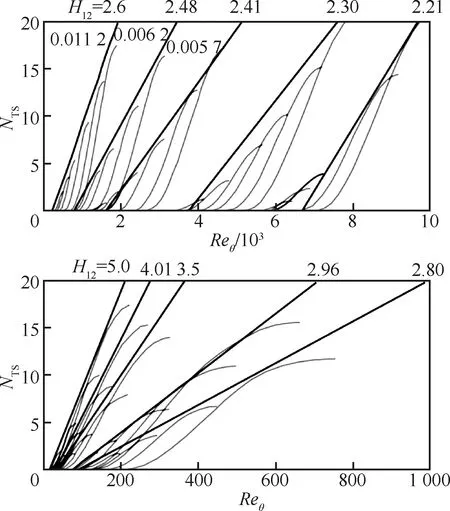
圖19 Blasius邊界層內(nèi)渦量雷諾數(shù)和動量厚度雷諾數(shù)關(guān)系圖[7]
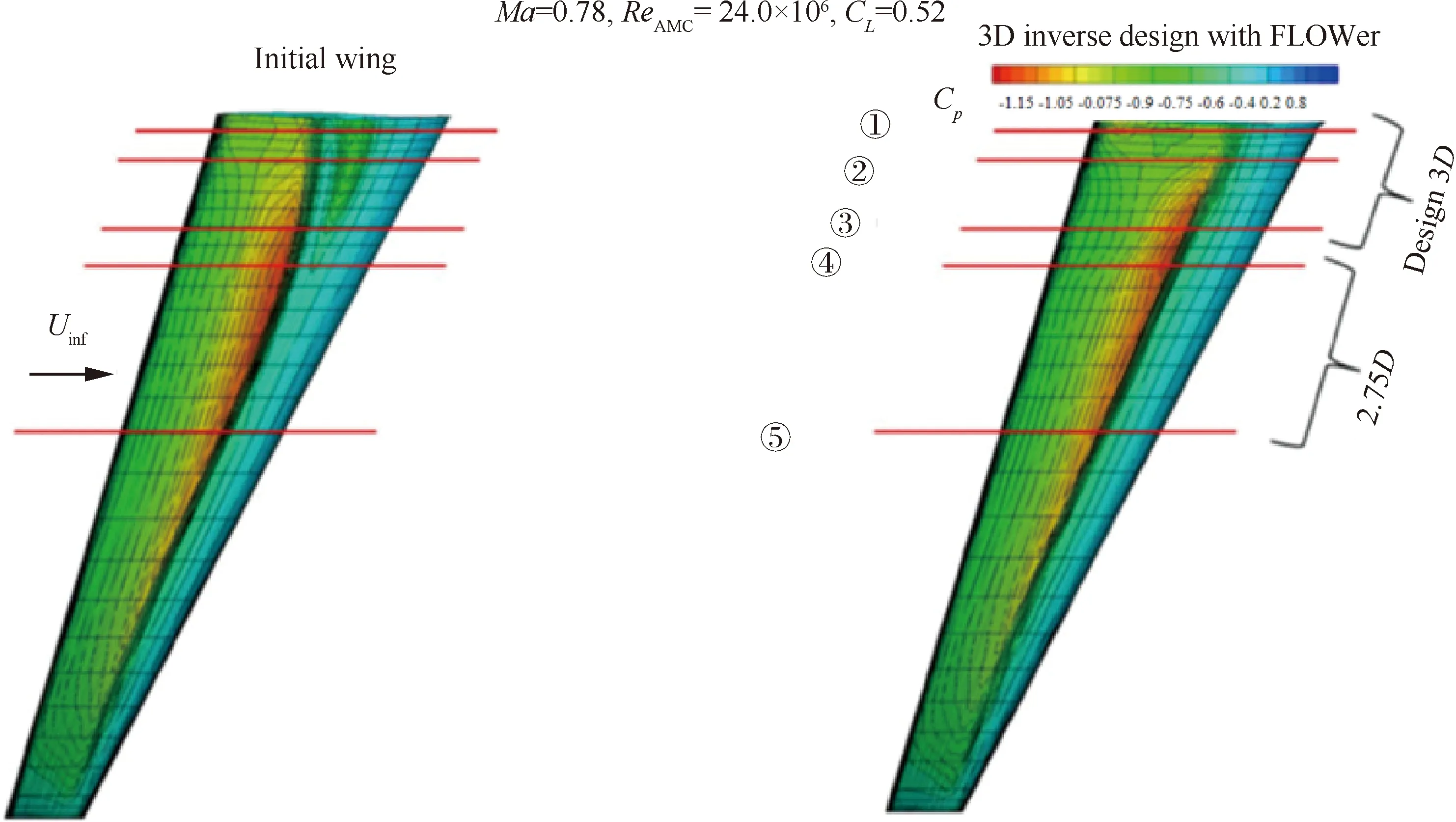
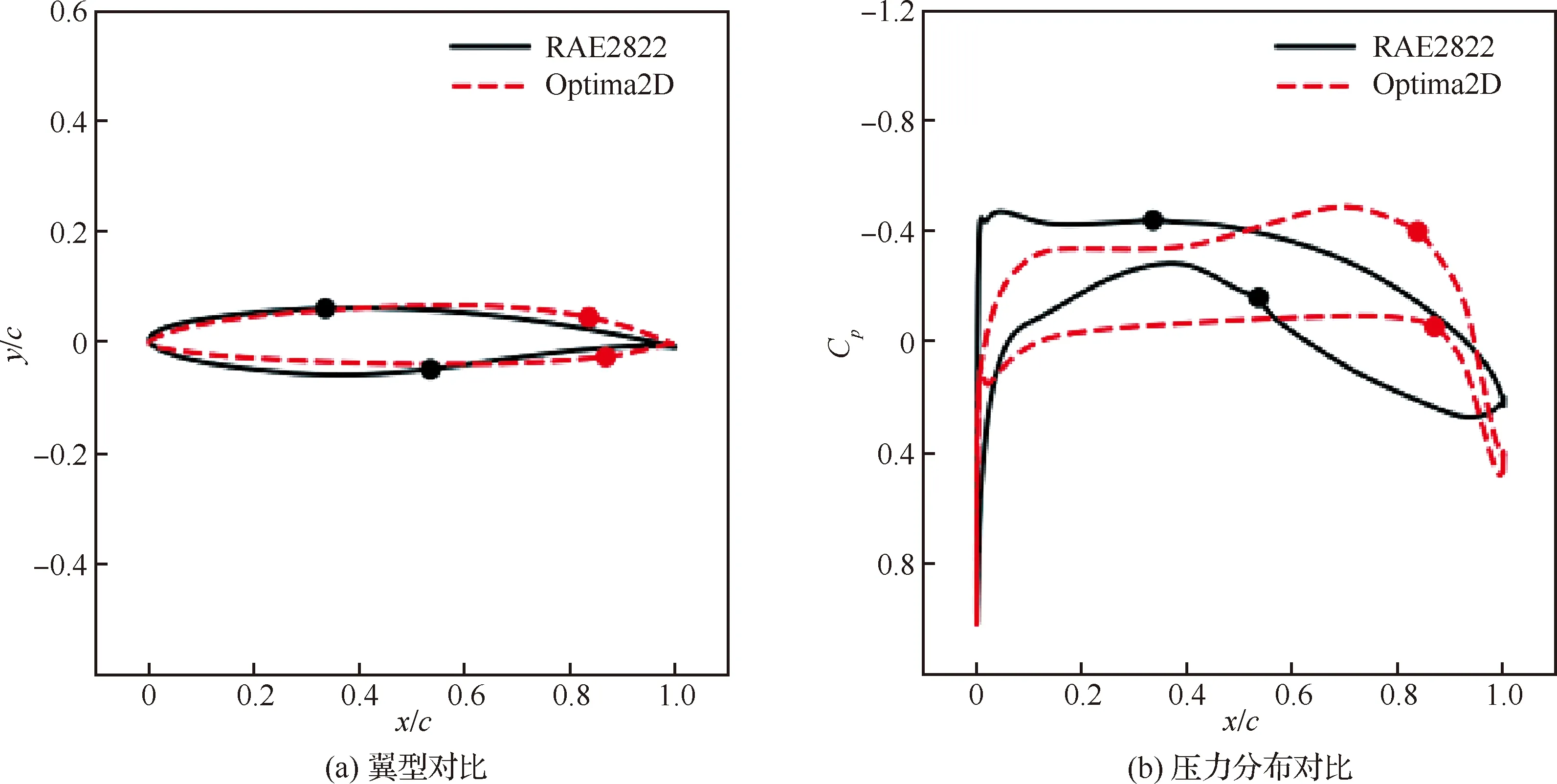
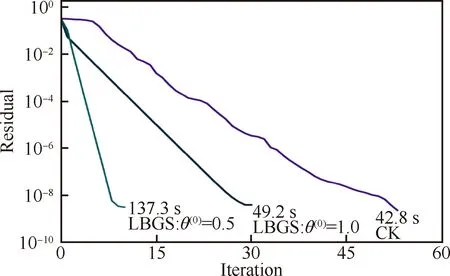
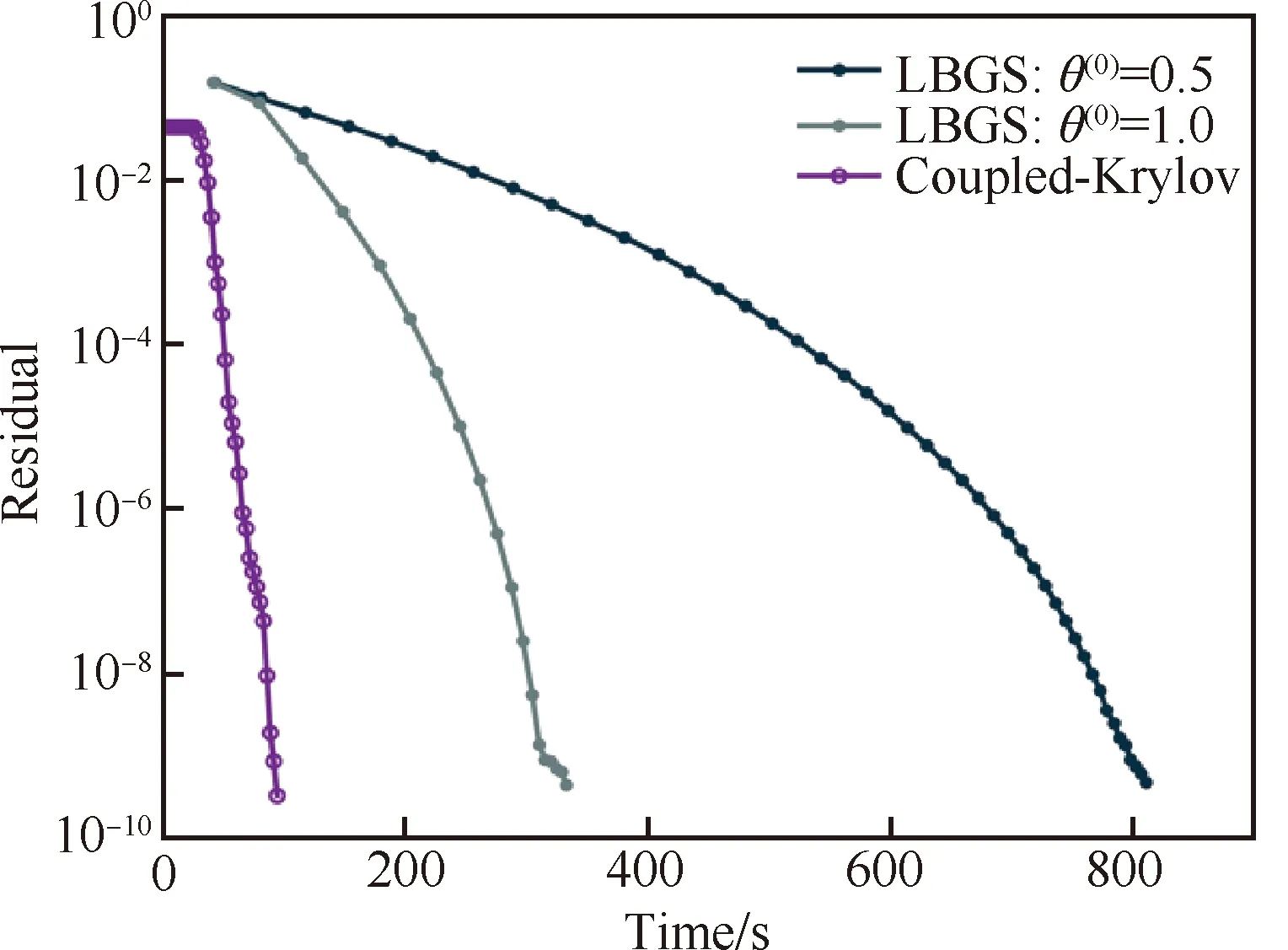
(11)
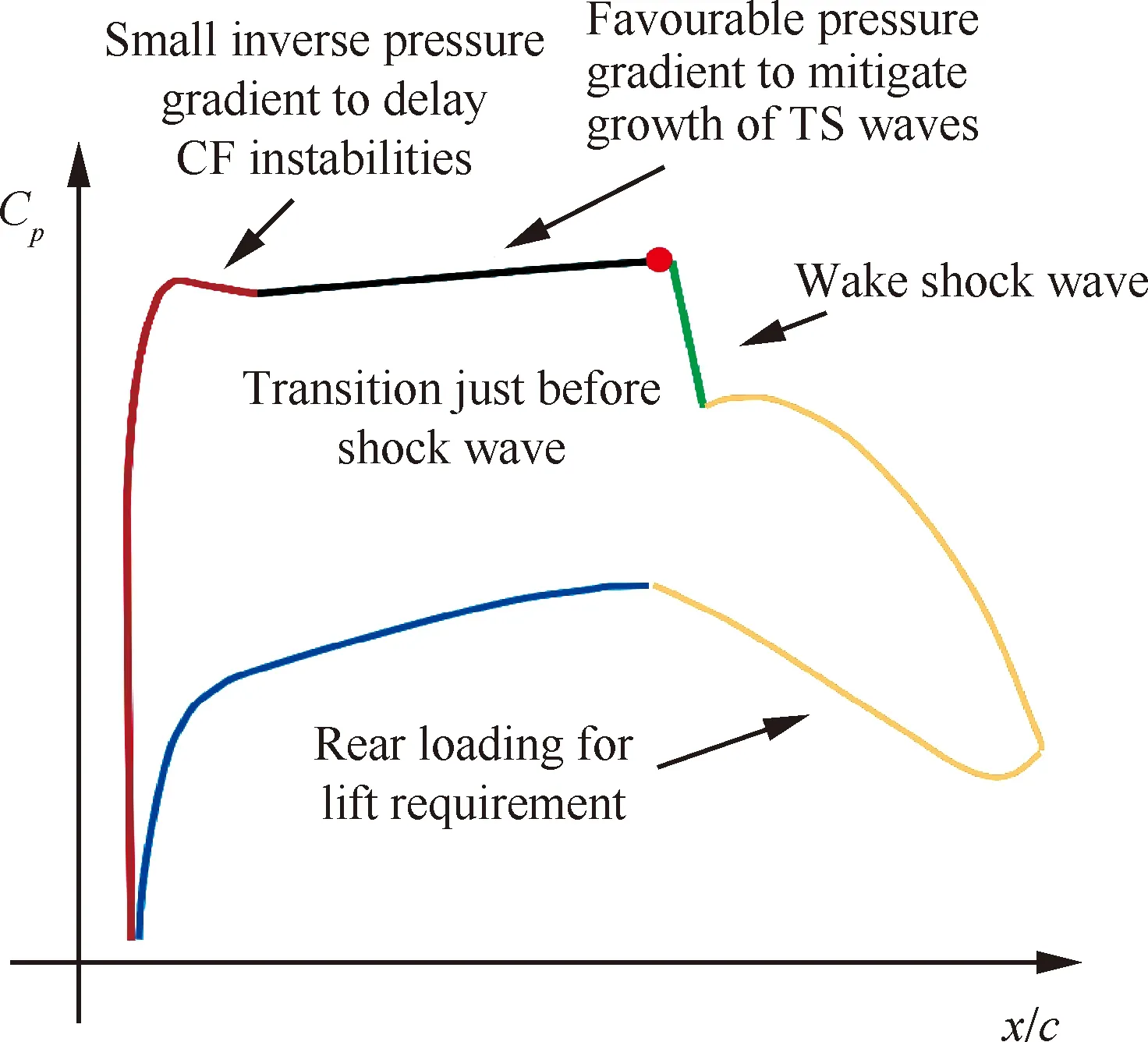
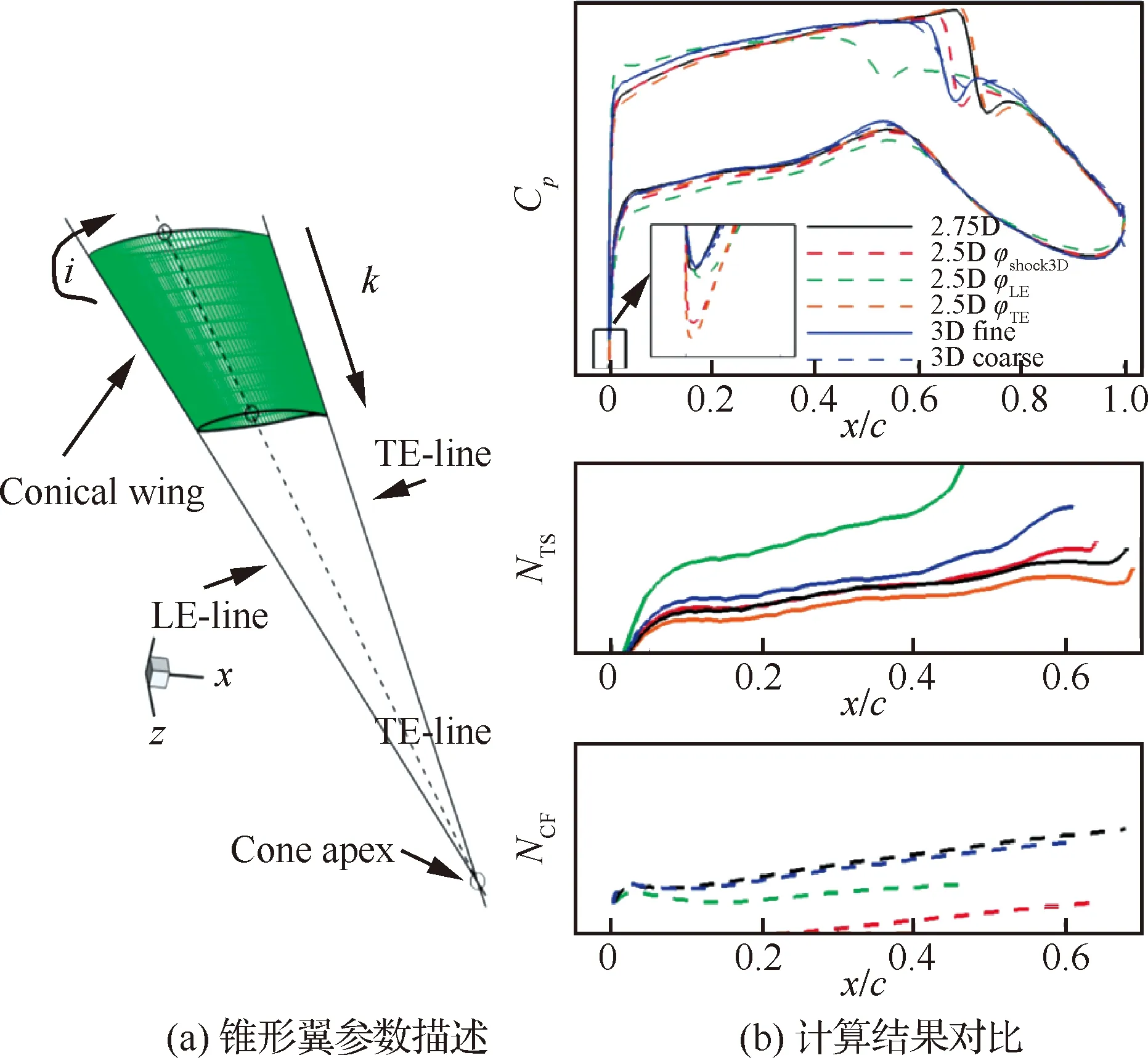
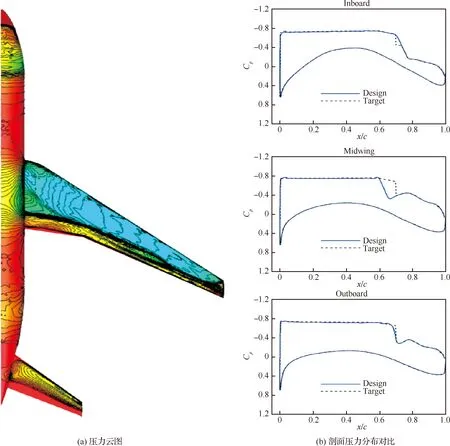
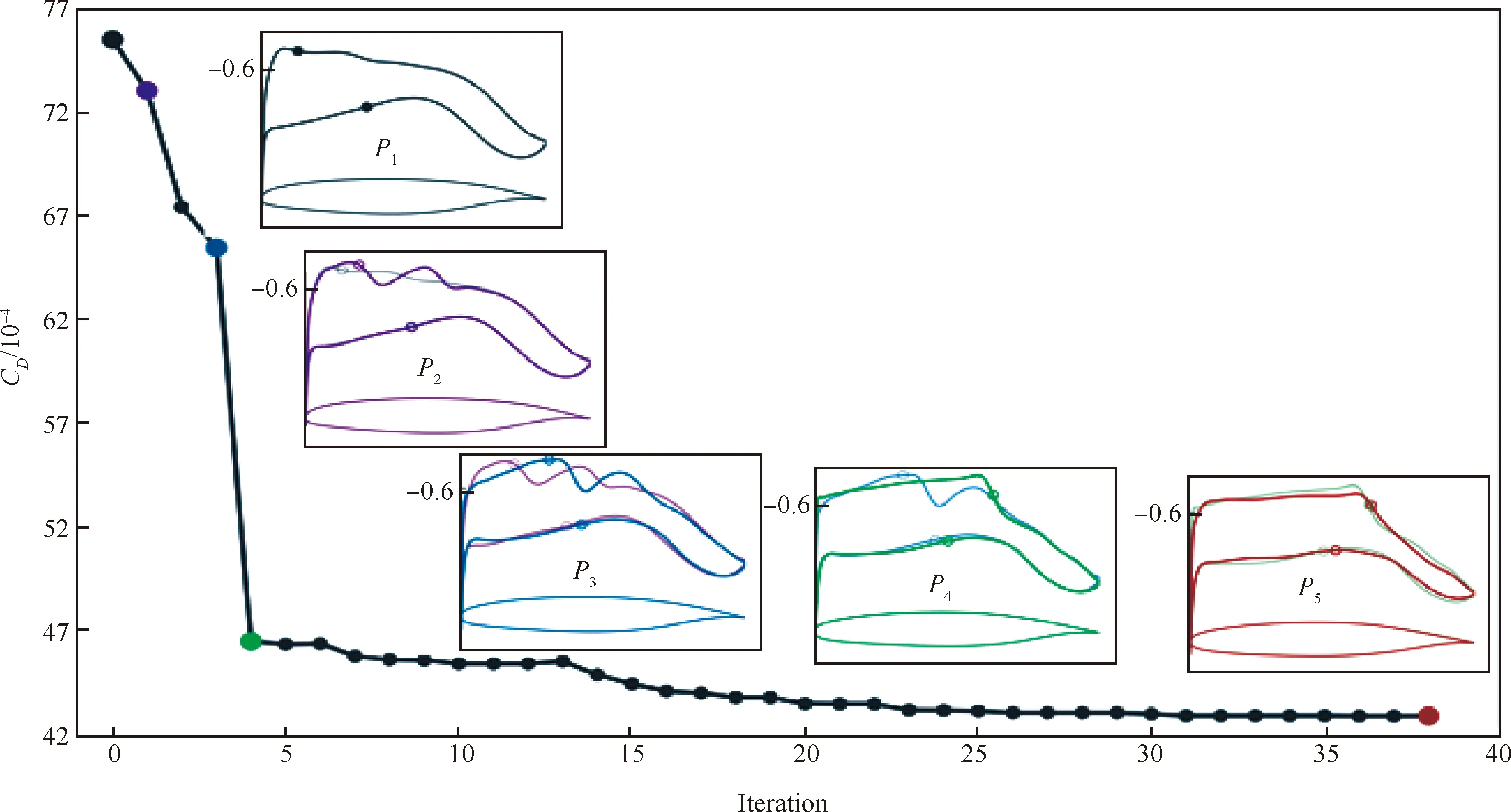
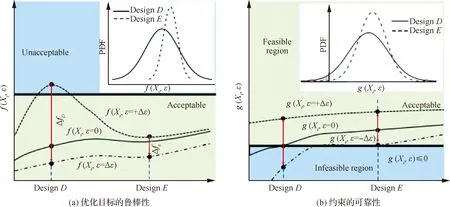
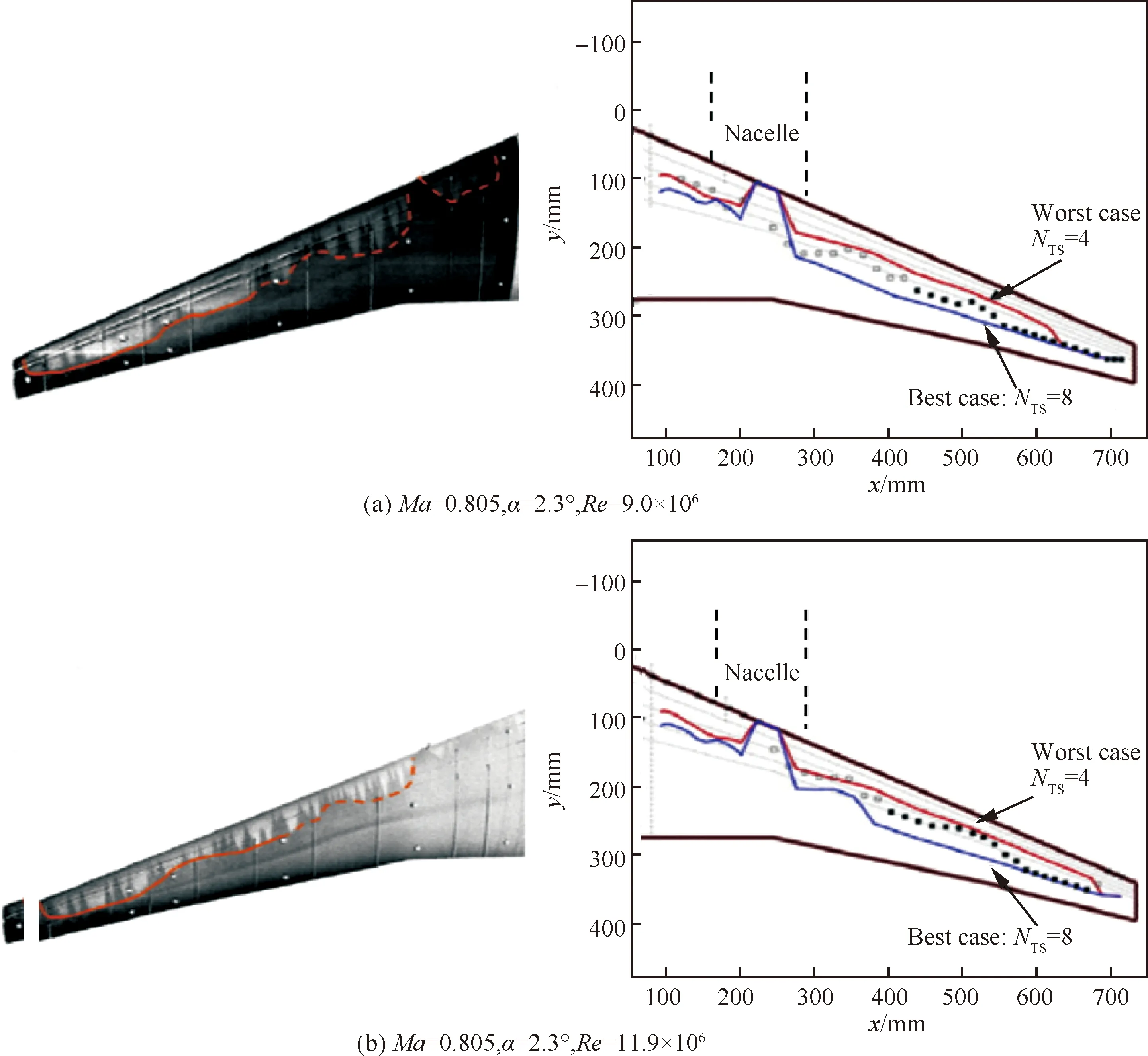
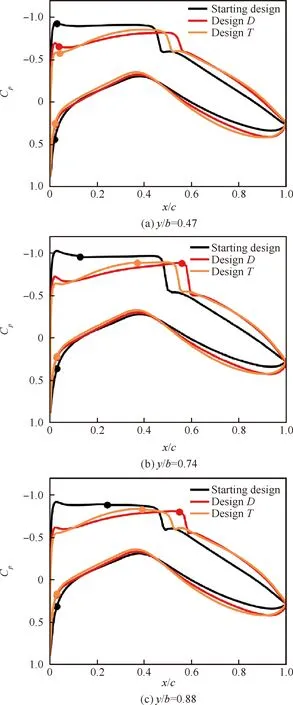
當(dāng)形狀因子H12范圍在2.3 圖20 最大渦量雷諾數(shù)與動量厚度雷諾數(shù)相對誤差隨形狀因子變化示意圖[6] Coder等[91]基于輸運方程的思想,結(jié)合Drela提出的擾動放大因子關(guān)系式,建立了放大因子輸運(Amplification Factor Transport)方程。Drela建立了放大因子和動量厚度雷諾數(shù)的關(guān)系,見圖21。該關(guān)系式基于穩(wěn)定理論,是從物理機理角度構(gòu)建轉(zhuǎn)捩預(yù)測模型的。在輸運方程的建立中,Coder也建立了當(dāng)?shù)乩字Z數(shù)與動量厚度雷諾數(shù)的關(guān)系式,以當(dāng)?shù)鼗麄€方程N的求解。之后,Oberkmpf等[92]通過改進形狀因子,使得N因子輸運方程遵守Galilean不變形。國內(nèi)徐家寬[93]和史亞云[94]等基于不同湍流模型研究了該輸運方程,并通過不同算例,驗證了該模型的精度。徐家寬等[95]基于線性穩(wěn)定理論和C1準(zhǔn)則還提出考慮橫流的N因子輸運方程,驗證結(jié)果表明拓展的模型可預(yù)測NLF(2)-0415、橢球、鐮刀翼(Sickle wing)等橫流轉(zhuǎn)捩現(xiàn)象。 圖21 不同形狀因子下擾動放大積分N因子與動量厚度雷諾數(shù)的關(guān)系[91] Walters等[96]還提出了層流脈動方程,該模型起源于斯坦福大學(xué)Bradshaw通過試驗提出的分裂機制概率,其認(rèn)為轉(zhuǎn)捩區(qū)的能力可分為層流動能和湍流動能兩個部分。層流動能主要在轉(zhuǎn)捩前和轉(zhuǎn)捩過程中放大擾動、傳遞能力最終猝發(fā)轉(zhuǎn)捩。轉(zhuǎn)捩過程被描述為能量傳遞和轉(zhuǎn)換過程。Walters等[96]建立的kL-kT-ε實現(xiàn)了對轉(zhuǎn)捩起止點的精確預(yù)測。王亮等[97]基于層流脈動黏性系數(shù)提出了k-ω-γ三方程模型,可模擬自然轉(zhuǎn)捩、旁路轉(zhuǎn)捩和橫流渦誘導(dǎo)轉(zhuǎn)捩。徐晶磊等[98]提出了湍動能一方程轉(zhuǎn)捩模型,基于尺度自適應(yīng)湍流模型重新標(biāo)定模型參數(shù),實現(xiàn)了層流/湍流的一體化計算,并針對經(jīng)典算例進行了驗證。 本節(jié)針對層流翼優(yōu)化設(shè)計總結(jié)了非梯度類優(yōu)化、梯度優(yōu)化以及不確定性分析和魯棒優(yōu)化,討論了層流翼氣動設(shè)計與全湍流氣動設(shè)計問題的異同點,梳理了NLF和HLFC機翼氣動設(shè)計理論。 基于非梯度類算法的優(yōu)化方法在飛行器氣動設(shè)計領(lǐng)域內(nèi),特別是全湍流氣動設(shè)計問題中得到了廣泛應(yīng)用[99-103]。常見的非梯度類算法包括遺傳算法 (Genetic Algorithm, GA)[104-105]、例子粒子群算法(Particle Swarm Optimization, PSO)[106-107]、差分進化算法(Differential Evolution, DE)[108-109]等。非梯度類算法無需對求解器進行修改,可方便的與各個模塊進行耦合,因此具有簡單、易實現(xiàn)、模塊化設(shè)計的特點。 非梯度類算法往往采用群體搜索策略,通過迭代計算以較大概率得到最優(yōu)解。為了逼近全局最優(yōu)解,群體搜索策略決定了需要可觀的種群規(guī)模以及足夠的迭代次數(shù)。并且優(yōu)化問題設(shè)計變量個數(shù)越多,需要的種群規(guī)模越大。這無疑增加了優(yōu)化過程中調(diào)用CFD求解器的次數(shù)。因此,非梯度類算法面臨“維度災(zāi)難”問題。為了提高非梯度類算法的優(yōu)化效率,除改進算法自身性能外,氣動優(yōu)化設(shè)計領(lǐng)域發(fā)展了一系列優(yōu)化方法及優(yōu)化策略,如基于低可信度或者混合精度CFD求解器的優(yōu)化策略、基于代理模型的優(yōu)化設(shè)計方法,設(shè)計空間降維方法等。文獻[110-113]對相關(guān)優(yōu)化方法的原理進行了較為詳細的綜述。 非梯度類算法模塊化、可移植性強的特點使得面向全湍流氣動設(shè)計的優(yōu)化方法和策略,基本可直接推廣至層流翼的氣動優(yōu)化設(shè)計。本文不再對相同方法原理進行重復(fù)贅述。按照優(yōu)化設(shè)計邏輯,基于非梯度類算法的層流翼優(yōu)化可分為直接優(yōu)化設(shè)計和反設(shè)計。 1) 直接優(yōu)化設(shè)計 利用基于全速勢、Euler的低可信度求解器耦合eN方法進行NLF翼型/機翼氣動設(shè)計,在層流翼設(shè)計方法發(fā)展初期得到了較廣泛的研究[114-115]。低可信度求解方法的使用,以設(shè)計精度損失為代價降低NLF翼型/機翼氣動優(yōu)化問題的計算規(guī)模。 針對計算花費較高的基于高可信度CFD求解器的層流翼氣動優(yōu)化設(shè)計問題,Zhang等[116]針對小后掠機翼,在優(yōu)化過程中采用固定轉(zhuǎn)捩計算策略,將順壓力梯度作為流場特征約束條件,保證優(yōu)化結(jié)果的真實轉(zhuǎn)捩位置與預(yù)估的固定轉(zhuǎn)捩位置相匹配。通過該近似處理減小層流翼優(yōu)化的計算量。Han等[82]采用Kriging代理模型和并行混合加點方法開展具有17°前緣后掠角的NLF超臨界機翼氣動優(yōu)化設(shè)計。設(shè)計馬赫數(shù)0.75,雷諾數(shù)20.0×106。Tang等[117]借助Kriging代理模型和混合優(yōu)化算法,開展了考慮流量系數(shù)和幾何約束的軸對稱NLF短艙多目標(biāo)氣動優(yōu)化設(shè)計。 為了提高設(shè)計結(jié)果在非設(shè)計點的魯棒性,F(xiàn)an等[118]添加了局部壓力分布特征目標(biāo)函數(shù),通過在氣動減阻尋優(yōu)過程中匹配給定的局部壓力分布特征,在一定程度上將設(shè)計經(jīng)驗引入基于代理模型的NLF機翼優(yōu)化設(shè)計中。但是,相比層流超臨界機翼氣動力系數(shù),壓力分布特征的預(yù)測難度更大,需要更大的樣本容量保證壓力分布的預(yù)測精度。 在HLFC機翼氣動優(yōu)化設(shè)計研究方面,白俊強[81]、楊體浩[56]、史亞云[119]等以無限展長后掠翼為對象,借助基于非梯度算法的直接優(yōu)化設(shè)計方法探究、梳理了HLFC機翼設(shè)計要點。 Shi等[120]采用RBF代理模型和微分進化算法,針對二維翼型,以吸氣孔位置、孔間距以及吸氣系數(shù)為設(shè)計變量,開展了HLFC吸氣控制參數(shù)優(yōu)化設(shè)計研究。相比初始構(gòu)型,優(yōu)化構(gòu)型轉(zhuǎn)捩位置推遲了17%,氣動阻力減小12.1%。Sudhi等[121]針對Ma=0.4的低亞聲速HLFC翼型,采用NSGA Ⅱ優(yōu)化算法,以包括吸氣控制位置、分布在內(nèi)的吸氣控制參數(shù),以及幾何為設(shè)計變量,開展考慮吸氣控制系統(tǒng)能耗懲罰的多點氣動設(shè)計。研究表明最優(yōu)吸氣控制位置與設(shè)計翼型具體的壓力分布特征息息相關(guān)。進一步,Sudhi等[122]以具有22.5°前緣后掠角的無限展長后掠翼為對象,在Ma=0.78、Re=30.0×106條件下開展NLF和HLFC機翼氣動設(shè)計,并進行了性能對比。設(shè)計結(jié)果表明,HLFC設(shè)計機翼的型阻比NLF機翼設(shè)計結(jié)果小43%。 基于傳統(tǒng)非梯度類算法的NLF/HLFC機翼直接優(yōu)化設(shè)計在探索、揭示層流超臨界機翼轉(zhuǎn)捩抑制原理和設(shè)計準(zhǔn)則方面發(fā)揮了重要作用。 圖22和圖23分別給出了小后掠NLF超臨界機翼、中等后掠角NLF超臨界機翼典型壓力分布特征。對于小后掠NLF機翼,TS波失穩(wěn)是導(dǎo)致層流-湍流轉(zhuǎn)捩的主要機制。因此,有利于層流保持的壓力分布形態(tài)為:擁有較低的頭部峰值,維持大范圍的順壓梯度,以弱激波形式實現(xiàn)壓力恢復(fù)。大范圍的順壓梯度可抑制TS波的快速發(fā)展。對于中等后掠NLF機翼,TS波和CF渦均為可觸發(fā)層流-湍流轉(zhuǎn)捩的主要機制。因此,中等后掠NLF機翼呈現(xiàn)出明顯不同于小后掠NLF機翼的壓力分布特征。具有大小適宜的頭部峰值避免過高峰值引起CF渦在前緣快速增長,峰值之后維持一定的逆壓力梯度或壓力平頂區(qū)來抑制或延緩CF渦的發(fā)展。之后為具有一定大小的順壓梯度抑制TS波的發(fā)展。最后以弱激波的形式進行壓力恢復(fù)。 圖22 小掠角NLF超臨界機翼典型壓力分布特征 圖23 中等掠角NLF超臨界機翼典型壓力分布特征 設(shè)計氣動性能優(yōu)異的HLFC機翼,需綜合權(quán)衡摩擦阻力、壓差阻力、激波強度、配平阻力以及吸氣控制的能量消耗。對于HLFC機翼,非均勻吸氣通過改變吸氣分布來提高吸氣控制效率,同等吸氣體積流量下,相比均勻吸氣控制,非均勻吸氣控制具有更好的轉(zhuǎn)捩抑制效果。配合有利壓力分布特征的轉(zhuǎn)捩抑制效果,HLFC機翼憑借較小的吸氣控制強度,便可實現(xiàn)層流轉(zhuǎn)捩的顯著推遲。在給定吸氣控制參數(shù)條件下,馬赫數(shù)、升力系數(shù)的變化,通過改變機翼壓力分布形態(tài)影響HLFC機翼氣動性能的魯棒性。適當(dāng)調(diào)整壓力分布形態(tài)的魯棒性并增大吸氣控制強度,可有效增強HLFC機翼氣動特性的魯棒性。通常吸氣控制區(qū)域越接近轉(zhuǎn)捩點上游,吸氣控制的轉(zhuǎn)捩抑制效果越明顯。 盡管基于非梯度類算法的傳統(tǒng)優(yōu)化方法具有互通性,但是層流翼優(yōu)化問題仍表現(xiàn)出一定自身特點。一方面,優(yōu)化過程中,單次CFD數(shù)值模擬計算量增大。對于基于輸運方程的轉(zhuǎn)捩預(yù)測方法,控制方程復(fù)雜度的提高增大了數(shù)值求解的計算量。對于基于松耦合策略的RANS-eN數(shù)值評估方法,在優(yōu)化算法大循環(huán)迭代基礎(chǔ)上,增加了保證轉(zhuǎn)捩計算收斂的內(nèi)循環(huán)次數(shù);另一方面,幾何設(shè)計變量與氣動性能參數(shù)間映射關(guān)系非線性特性增強。對于基于代理模型的優(yōu)化方法,高亞聲速流動中激波-附面層干擾呈現(xiàn)的非線性特征增大了提高代理模型預(yù)測精度的難度。層流超臨界翼型/機翼設(shè)計涉及轉(zhuǎn)捩控制問題。高亞聲速條件下,壓力分布-轉(zhuǎn)捩-氣動特性間復(fù)雜的非線性關(guān)系,進一步加大了提高代理模型預(yù)測精度的難度。 為了降低三維層流超臨界機翼氣動設(shè)計的難度,DLR[123]發(fā)展了一種基于截面錐形翼近似的層流機翼設(shè)計方法,其原理如圖24所示。該方法將三維超臨界機翼設(shè)計截面簡化為2.75D錐形翼設(shè)計。簡化的錐形翼的CFD數(shù)值模擬計算量與二維翼型相當(dāng)。與基于無限展長后掠翼(無根梢比)的2.5D設(shè)計方法相比,2.75D錐形翼設(shè)計同時兼顧了后掠及根梢比三維效應(yīng)影響(機翼前緣后掠角對CF渦不穩(wěn)定性和附著線轉(zhuǎn)捩影響顯著,機翼根梢比影響翼面上的激波掠角)。圖24顯示,相比不同后掠(包括:按機翼前緣后掠φLE、按機翼后緣掠角φTE及按激波掠角φshock3D)的2.5D 設(shè)計方法,2.75D設(shè)計方法在壓力分布形態(tài)、CF渦以及TS波發(fā)展方面與直接的3D設(shè)計方法更為接近。 圖24 基于截面錐形翼近似的層流翼設(shè)計方法[123] 近年快速發(fā)展的深度學(xué)習(xí)技術(shù)被引入至層流翼的氣動設(shè)計與分析問題中。Li等[124]借助生成對抗網(wǎng)絡(luò)和翼型模態(tài)表征法,發(fā)展了翼型特征篩選模型,通過濾掉不滿足幾何約束及幾何特征奇異的翼型,得到更為緊致的翼型設(shè)計空間,以提高基于非梯度算法的氣動優(yōu)化設(shè)計方法的效率。Li等[124]篩選模型嵌入基于代理模型的優(yōu)化框架,開展了低雷諾數(shù)層流翼型氣動優(yōu)化設(shè)計。篩選模型的構(gòu)建依賴于符合工程應(yīng)用需求的翼型數(shù)據(jù)庫。但是,對于包括超臨界層流機翼在內(nèi)的大部分氣動設(shè)計問題往往難以獲得可靠的翼型數(shù)據(jù)庫。Wang等[125]針對帶有微/納矩形肋的層流翼氣動減阻問題,借助人工神經(jīng)網(wǎng)絡(luò)將微/納米結(jié)構(gòu)近壁流動對流場的影響,以邊界條件的形式引入基于RANS方程的面向光滑層流翼的數(shù)值模擬中,近似考慮微/納矩形肋對層流翼氣動性能的影響。Wang等[125]通過簡化的多尺度數(shù)值模擬策略,提高微/納矩形肋影響下層流翼氣動分析與優(yōu)化設(shè)計的計算效率。 2) 反設(shè)計方法 相比基于非梯度算法的層流翼直接優(yōu)化設(shè)計方法,當(dāng)掌握了“壓力分布-轉(zhuǎn)捩-氣動性能”之間的映射關(guān)系,氣動反設(shè)計[126-127]成為一種層流翼高效設(shè)計方法。 層流翼反設(shè)計方法已被廣泛用于面向風(fēng)洞、飛行試驗的層流翼試驗?zāi)P偷脑O(shè)計。Yang等[128]建立了基于代理模型的HLFC機翼反設(shè)計方法,設(shè)計了具有35°前緣后掠角的垂尾翼套氣動外形,如圖25所示。在Ma=0.75、Re=38.1×106、-2°~2°側(cè)滑角工況下均可維持20%當(dāng)?shù)叵议L以上的層流區(qū)。 圖25 基于代理模型氣動反設(shè)計方法的HLFC垂尾翼套設(shè)計[128] Cella等[31]利用基于低可信度速勢方程的CFD求解器和GA算法的反設(shè)計方法,設(shè)計了具有20°前緣后掠的UW-5006 NLF超臨界機翼,如圖26所示。風(fēng)洞試驗結(jié)果表明典型工況上、下翼面均可維持40%弦長以上的層流范圍。 圖26 UW-5006 NLF超臨界機翼設(shè)計[31] 反設(shè)計方法的難點在于給出具有優(yōu)異氣動性能且物理可實現(xiàn)的目標(biāo)壓力分布。Campbell和Streit等[129]發(fā)展了一種可有效匹配指定流場特征的目標(biāo)壓力分布生成方法,以支持融合設(shè)計經(jīng)驗的層流翼反設(shè)計。轉(zhuǎn)捩預(yù)測采用eN方法。該設(shè)計方法不僅可添加包括壓力梯度在內(nèi)的壓力分布特征約束,還可施加TS及CF擾動波的N因子分布特征約束。N因子分布特征通過構(gòu)造指數(shù)多項式描述。Campbell等[79]利用構(gòu)建的反設(shè)計方法進行了CRM-NLF構(gòu)型氣動設(shè)計,實現(xiàn)了對附著線轉(zhuǎn)捩、TS波及CF渦失穩(wěn)觸發(fā)轉(zhuǎn)捩的有效抑制,如圖27所示。DLR的Seitz等[130]利用構(gòu)建的反設(shè)計方法,面向具有17°前緣前掠角的中短程前掠翼布局客機,設(shè)計了NLF超臨界機翼。在馬赫數(shù)0.78、雷諾數(shù)24.0×106的設(shè)計條件下,前掠翼上翼面可維持不小于60%弦長的層流區(qū),如圖28所示。 圖27 基于反設(shè)計方法CRM-NLF氣動設(shè)計[79] 圖28 基于反設(shè)計方法的前掠翼氣動設(shè)計[130] NASA的Lynde等[131]針對采用分布式動力的電動支線客機,借助反設(shè)計方法設(shè)計了巡航馬赫數(shù)0.785、雷諾數(shù)23.0×106的NLF超臨界機翼。反設(shè)計過程引入了上翼面最大曲率約束以及最大逆壓力梯度流場約束,以此控制非設(shè)計條件下NLF超臨界機翼的激波強度,同時避免過早出現(xiàn)流動分離現(xiàn)象。 基于非梯度算法的氣動優(yōu)化方法具有的較強通用性,使得面向?qū)恿饕須鈩釉O(shè)計問題的相關(guān)研究,無論是直接優(yōu)化設(shè)計還是反設(shè)計,基本均沿襲面向全湍流氣動設(shè)計的優(yōu)化方法。相比全湍流氣動設(shè)計問題,層流翼氣動優(yōu)化具有更大的計算量,更強的設(shè)計空間非線性特性,更突出的“維度災(zāi)難”現(xiàn)象。現(xiàn)有研究通常在已有優(yōu)化方法框架下通過引入局部壓力分布特征等約束/目標(biāo)來調(diào)整優(yōu)化設(shè)計策略,以適應(yīng)層流翼氣動優(yōu)化設(shè)計問題。發(fā)展匹配層流翼氣動設(shè)計問題特點的高效、可靠的非梯度優(yōu)化設(shè)計方法的研究較少。 近些年,基于離散伴隨的梯度優(yōu)化被廣泛認(rèn)為是未來全機一體化設(shè)計最為有效的解決途徑。從圖29可以看出,非梯度優(yōu)化算法調(diào)用的CFD計算次數(shù)與設(shè)計變量個數(shù)呈二次或者三次方增長關(guān)系,而梯度優(yōu)化是線性增長關(guān)系。梯度優(yōu)化的關(guān)鍵在于梯度信息的高效、精確求解。基于伴隨理論的求解方法使得梯度信息計算成本不依賴于設(shè)計變量個數(shù),從而得到了廣泛的發(fā)展和應(yīng)用。控制方程的伴隨方程主要有兩種形式:連續(xù)伴隨和離散伴隨。連續(xù)伴隨依賴于網(wǎng)格疏密,難以保證計算精度,同時大量針對控制方程的推導(dǎo)對開發(fā)者提出苛刻的要求。基于離散伴隨方程結(jié)合自動微分技術(shù)、無矩陣存儲技術(shù)、鏈?zhǔn)角髮?dǎo)法則等先進技術(shù)的梯度優(yōu)化方法目前得到了重點發(fā)展。MDOlab團隊[132-133]針對全湍流設(shè)計問題,采用基于離散伴隨理論的梯度優(yōu)化方法進行了大量全機一體化設(shè)計研究,包括CRM標(biāo)模[133]、“雙泡”D8飛機[134]、支撐翼布局飛機[135]等。研究成果表明,基于離散伴隨理論的梯優(yōu)化方法可滿足未來一體化設(shè)計的要求。 圖29 非梯度/梯度優(yōu)化方法中CFD計算次數(shù)與設(shè)計變量的關(guān)系示意圖[132-133] 層流技術(shù)在未來工程轉(zhuǎn)化過程中也將面臨全機一體化這種具有大規(guī)模設(shè)計變量的氣動設(shè)計問題。國內(nèi)外學(xué)者針對層流翼設(shè)計初步開展了基于伴隨理論的梯度優(yōu)化設(shè)計研究。Pralits[136]和Amoignon[137]等基于Euler方程耦合拋物化理論進行了層流翼的優(yōu)化設(shè)計研究。該研究推導(dǎo)了拋物化方程的連續(xù)伴隨方程,從擾動能量的觀點優(yōu)化混合層流的吸氣分布,以降低吸氣功耗。同時,將該梯度優(yōu)化推廣到三維自然層流翼優(yōu)化,目標(biāo)函數(shù)考慮了總阻力,最終實現(xiàn)推遲轉(zhuǎn)捩及減阻的目標(biāo)。該方法在耦合計算過程中,沒有進行迭代,也沒有考慮總阻力對設(shè)計變量的梯度,僅是將阻力作為目標(biāo)函數(shù),并通過擾動能量來推遲轉(zhuǎn)捩位置。此外,連續(xù)伴隨梯度求解依賴網(wǎng)格疏密程度,無法有效保證梯度求解精度,限制了該層流翼優(yōu)化方法的發(fā)展。 Lee等[141]耦合了基于離散伴隨的RANS求解器和eN方法,進行了層流機翼的梯度優(yōu)化設(shè)計。其中,通過數(shù)據(jù)庫方法進行擾動增長率計算。在梯度求解過程中,Lee等[141]沒有考慮轉(zhuǎn)捩部分的梯度求解,即在求解離散伴隨方程時凍結(jié)了轉(zhuǎn)捩位置。圖30給出的優(yōu)化結(jié)果顯示,雖然氣動阻力明顯減小,但是轉(zhuǎn)捩位置反而提前。優(yōu)化過程降低了壓差阻力,但沒有降低摩擦阻力。該研究結(jié)果顯示,由于梯度信息不準(zhǔn)確的求解,顯著限制了梯度優(yōu)化算法的尋優(yōu)效果,無法有效挖掘?qū)恿饕淼木薮鬁p阻潛力。 圖30 后掠翼層流優(yōu)化設(shè)計結(jié)果示意圖[141] Driver等[142]結(jié)合二維RANS求解器和MESE進行轉(zhuǎn)捩預(yù)測,該RANS求解器具備基于離散伴隨理論的梯度求解能力。為了考慮轉(zhuǎn)捩預(yù)測模型對梯度信息的貢獻,Driver通過有限差分獲得相關(guān)轉(zhuǎn)捩梯度信息。 Rashad等[143]在Driver的研究工作基礎(chǔ)上,基于全湍流流動離散伴隨方程,推導(dǎo)了考慮層流轉(zhuǎn)捩的耦合伴隨方程。增廣的伴隨方程雅可比矩陣包含了RANS方程、轉(zhuǎn)捩模擬兩個模塊的交叉導(dǎo)數(shù)項。該方程從理論上保證了考慮轉(zhuǎn)捩的梯度信息的準(zhǔn)確求解。Rashad等[143]提出了非迭代(Noniterative)策略求解耦合伴隨方程,大大提高了傳統(tǒng)基于LBGS(Linear Block Gauss Seidel)方法的耦合伴隨方程的求解效率。Rashad同時對比了復(fù)變量微分/有限差分和基于離散伴隨方法求解的梯度信息。對比結(jié)果顯示,離散伴隨方法可更精確、可靠的獲得梯度信息。Rashad等[143]將建立的梯度優(yōu)化方法應(yīng)用在層流翼型的優(yōu)化設(shè)計中。圖31給出的RAE2822優(yōu)化結(jié)果顯示,經(jīng)過優(yōu)化設(shè)計轉(zhuǎn)捩位置被有效推遲。優(yōu)化后上、下翼面分別維系了72.3%和76.8%弦長的層流區(qū)。壓差阻力和摩擦阻力均得到顯著降低。之后,Rashad等[143]還成功進行了跨聲速層流翼型的多點優(yōu)化設(shè)計研究。 圖31 RAE2822層流優(yōu)化設(shè)計結(jié)果對比示意圖[143] Rashad等[143]建立的基于離散伴隨理論的層流翼優(yōu)化設(shè)計方法,在理論上可精確考慮轉(zhuǎn)捩模塊對梯度信息的影響。但是,在構(gòu)造伴隨方程過程中,由于雅可比矩陣的計算采用的是復(fù)變量微分/有限差分法,顯著影響了伴隨方程構(gòu)造的計算效率及精度。目前,該方法僅應(yīng)用在二維翼型的優(yōu)化問題中。對于三維復(fù)雜構(gòu)型,由于伴隨方程的雅克比矩陣的維度非常龐大,使得通過復(fù)變量微分/有限差分法計算雅克比矩陣的途徑,無法滿足未來面向全機一體化設(shè)計趨勢,發(fā)展層流翼高效梯度優(yōu)化設(shè)計方法的需求。 Shi等[72]基于具有離散伴隨功能的結(jié)構(gòu)求解器,并耦合eN方法,推導(dǎo)了耦合伴隨方程,即 (12) 式中:?R/?Q為RANS殘差方程關(guān)于RANS狀態(tài)變量Q的偏導(dǎo)數(shù)矩陣;?Q/?Tr為RANS殘差方程關(guān)于轉(zhuǎn)捩狀態(tài)變量Tr的偏導(dǎo)數(shù)矩陣;?L/?Q為轉(zhuǎn)捩模型殘差關(guān)于RANS狀態(tài)變量Q的偏導(dǎo)數(shù)矩陣;?L/?Tr為轉(zhuǎn)捩模型殘差關(guān)于轉(zhuǎn)捩位置/長度的偏導(dǎo)數(shù)矩陣,該項為單位矩陣;ψ和φ分別是和RANS方程狀態(tài)變量與轉(zhuǎn)捩狀態(tài)變量相關(guān)的伴隨向量;?I/?Q、?I/?Tr分別為目標(biāo)函數(shù)對RANS方程狀態(tài)變量和轉(zhuǎn)捩狀態(tài)變量的偏導(dǎo)數(shù)。對于新增的3個雅可比矩陣,Shi等[72]繼承了原有湍流模型采用無矩陣存儲技術(shù)求解雅可比矩陣的方法,即獲得的是相關(guān)雅可比矩陣向量,包括:(?R/?Q)ψ, (?R/?Tr)φ, (?L/?Tr)φ以及(?R/?Q)ψ。結(jié)合鏈?zhǔn)角髮?dǎo)法則和反向自動微分技術(shù),最終可精確求得相關(guān)雅可比矩陣向量。 進一步,Shi等分別使用傳統(tǒng)LBGS(Linear Block Gauss-Seidel)算法和CK(Coulped Krylov)算法求解耦合伴隨方程。同時,針對二維翼型和三維后掠翼,對比了兩種伴隨方程求解算法的效率,見圖32和圖33。研究結(jié)果表明,傳統(tǒng)的LBGS的計算效率受松弛因子θ影響顯著。并且,無論二維翼型還是三維后掠翼,CK求解效率均遠高于LBGS方法。最終,結(jié)合優(yōu)化設(shè)計輔助技術(shù),建立了層流翼梯度優(yōu)化設(shè)計框架,見圖34。圖中X為氣動設(shè)計變量,C為約束函數(shù),xs、xv分別為物面和空間網(wǎng)格坐標(biāo)。 圖32 層流翼型采用不同耦合伴隨求解策略收斂歷程對比[72] 圖33 無限展長后掠層流翼采用不同耦合伴隨求解策略收斂歷程對比[72] 圖34 層流翼梯度優(yōu)化設(shè)計框架[72] 基于建立的層流翼優(yōu)化框架,Shi等[72]分別進行了二維層流翼型的單點和多點優(yōu)化設(shè)計,以及考慮多種轉(zhuǎn)捩機制的后掠翼優(yōu)化設(shè)計。圖35給出的單點層流翼型優(yōu)化結(jié)果顯示,優(yōu)化翼型有效抑制了TS波擾動,使得轉(zhuǎn)捩得到顯著推遲。同時,該研究還對比了凍結(jié)轉(zhuǎn)捩位置的優(yōu)化設(shè)計,即在優(yōu)化過程中不考慮轉(zhuǎn)捩預(yù)測,但是最終優(yōu)化結(jié)果的數(shù)值模擬考慮轉(zhuǎn)捩計算。雖然凍結(jié)轉(zhuǎn)捩位置的優(yōu)化翼型的氣動阻力也得到了顯著減小,但減阻收益遠小于層流翼優(yōu)化設(shè)計結(jié)果。圖36給出了層流翼型的優(yōu)化收斂歷程,以及P1~P5次主迭代壓力分布的演變過程。梯度優(yōu)化在35步主迭代后達到收斂。 圖35 層流翼型單點優(yōu)化設(shè)計結(jié)果對比[72] 圖36 層流翼型單點梯度優(yōu)化收斂歷程[72] 圖37和圖38給出了參考Hondajet設(shè)計狀態(tài)的層流翼型多點優(yōu)化設(shè)計。優(yōu)化結(jié)果顯示,發(fā)展的層流翼梯度優(yōu)化方法,可實現(xiàn)形面設(shè)計與轉(zhuǎn)捩推遲誘發(fā)的氣動阻力成份間(摩擦阻力、激波阻力等)的有效權(quán)衡。 圖37 層流翼型多點優(yōu)化設(shè)計翼型對比[72] 圖38 層翼型多點優(yōu)化設(shè)計壓力分布與轉(zhuǎn)捩位置對比[72] Shi等[73]將發(fā)展的基于離散伴隨理論的梯度優(yōu)化方法進行了擴展,拓展到了可同時考慮TS波和CF渦擾動的三維層流翼優(yōu)化設(shè)計問題。圖39給出了針對具有25°后掠角的無限展長后掠層流翼,優(yōu)化前后的剖面翼型和壓力分布對比。優(yōu)化結(jié)果顯示,發(fā)展的層流翼梯度優(yōu)化方法可有效平衡抑制TS波和CF渦的矛盾,并實現(xiàn)氣動阻力成份間的有效權(quán)衡,最終達到氣動減阻的優(yōu)化目標(biāo)。圖40給出的梯度優(yōu)化收斂歷程圖表明,優(yōu)化收斂僅需38次主迭代,具有較高的優(yōu)化效率。 圖39 無限展長后掠層流翼優(yōu)化前后剖面翼型和壓力分布對比圖[73] 圖40 無限展長后掠層流翼梯度優(yōu)化收斂歷程[73] 目前,基于離散伴隨的層流翼梯度優(yōu)化設(shè)計方法還處在初步發(fā)展階段,且主要應(yīng)用在NLF設(shè)計中,鮮有針對HLFC機翼優(yōu)化設(shè)計的相關(guān)研究。此外現(xiàn)有研究對象相對簡單,主要圍繞二維翼型以及無限展長后掠翼。 對于實際工程問題,不確定性影響因素貫穿飛行器的整個生命周期,不可避免地導(dǎo)致飛行器性能出現(xiàn)波動,惡化飛行器性能,甚至造成一定安全隱患。2002 年,NASA推出了航空航天領(lǐng)域考慮不確定性影響的多學(xué)科優(yōu)化設(shè)計規(guī)劃[144],指出了不確定性影響下飛行器設(shè)計的難點和面臨的挑戰(zhàn)。 不確定性分析是從統(tǒng)計角度研究飛行器性能受隨機擾動影響的有效方法。通過分析隨機擾動的傳播、放大,量化其對性能參數(shù)的影響。與確定性優(yōu)化問題不同,考慮不確定性的魯棒設(shè)計將隨機擾動視為不確定性變量,通常把不確定性變量影響下性能參數(shù)的統(tǒng)計均值以及標(biāo)準(zhǔn)差引入優(yōu)化模型。 圖41以一維最小化約束優(yōu)化問題為例描述確定性優(yōu)化與考慮不確定性的魯棒優(yōu)化間的差異[145]。圖中:Xi為第i個確定性變量;ε為不確定性變量;f(·)為優(yōu)化目標(biāo)函數(shù);g(·)為約束函數(shù)。設(shè)計點D(XiD)為確定性優(yōu)化結(jié)果,設(shè)計點E(XiE)為考慮不確定性的魯棒設(shè)計結(jié)果。當(dāng)不確定性變量出現(xiàn)[-Δε,+Δε]區(qū)間擾動變化時,魯棒設(shè)計結(jié)果E的目標(biāo)函數(shù)波動較小,并且約束函數(shù)依然在可行域內(nèi)。相比之下,不確定性變量擾動下,確定性優(yōu)化結(jié)果D的目標(biāo)函數(shù)出現(xiàn)了大幅波動,甚至超過了可接受程度。在[-Δε,0)不確定性變量的擾動范圍內(nèi),其約束函數(shù)落在了非可行域內(nèi)。因此,從統(tǒng)計角度來看,雖然確定性優(yōu)化D的目標(biāo)函數(shù)具有更小的統(tǒng)計均值,但是方差較大,存在設(shè)計結(jié)果為不可行解的風(fēng)險。考慮不確定性的魯棒優(yōu)化E具有更強的魯棒性和可靠性。 圖41 確定性優(yōu)化與考慮不確定性的魯棒優(yōu)化間差異的說明示意圖[145] 目前,不確定性分析與魯棒設(shè)計在全湍流氣動設(shè)計問題中得到了大量應(yīng)用[146-150]。由于層流邊界層穩(wěn)定性對外界擾動的敏感性,使得層流翼氣動設(shè)計問題對考慮不確定性的魯棒設(shè)計的需求更為突出。 一方面,包括雷諾數(shù)、馬赫數(shù)、來流湍流度、云層和噪聲等在內(nèi)的基本流引入的隨機擾動,以及由于加工制造誤差、工藝能力限制、昆蟲污染等造成的幾何缺陷引入的擾動,對層流翼的層流保持能力影響明顯,甚至可能造成層流區(qū)范圍出現(xiàn)非預(yù)期的大幅度減小,氣動阻力大幅度增加,顯著惡化飛行器氣動性能。 Liu等[151]研究了壓敏漆涂層厚度對NLF翼型壓力分布和升力系數(shù)的影響進行了不確定性量化評估,分析結(jié)果指出壓敏漆涂層厚度引起的幾何理論外形的改變,是導(dǎo)致試驗測量誤差的主要直接原因。Yang等[152]圍繞層流翼飛行試驗,探究了運營條件和幾何不確定性影響下NLF及HLFC機翼氣動性能的統(tǒng)計響應(yīng)特征。研究表明,包括攻角和巡航馬赫數(shù)在內(nèi)的運營條件不確定性對層流翼的層流保持能力影響顯著。與NLF機翼不同,隨機擾動通過同時改變壓力梯度以及吸氣控制參數(shù)來影響HLFC機翼的氣動性能。DLR的Barklage等[153]針對HLFC機翼,量化評估了由于加工制造和儀器測量誤差引入的壓力分布、吸氣腔體靜壓及吸氣壁板屬性不確定性對HLFC機翼吸氣控制參數(shù)的影響。分析結(jié)果顯示壓力分布及吸氣壁板屬性參數(shù)的測量誤差是導(dǎo)致HLFC機翼吸氣控制參數(shù)不確定性增大的主要原因。Pohya等[154]基于民機整個生命周期,從統(tǒng)計角度評估了運營條件、大氣環(huán)境、燃油價格等不確定性因素對HLFC機翼綜合收益的影響,并指出運營條件不確定性,特別是巡航速度擾動是引起HLFC機翼綜合收益不確定性增大的最主要原因。設(shè)計具有更強抵抗巡航速度擾動變化能力的魯棒HLFC機翼,減小層流邊界層對運營條件變化的敏感性,是降低HLFC機翼綜合收益不確定性的有效途徑之一。 另一方面,層流-湍流轉(zhuǎn)捩的精確預(yù)測是一個復(fù)雜的科學(xué)問題。目前面向工程應(yīng)用的無論是輸運形式的轉(zhuǎn)捩模型還是基于穩(wěn)定性理論的轉(zhuǎn)捩預(yù)測方法,均存在模型構(gòu)建及使用過程中引入的認(rèn)知不確定性。以基于線性穩(wěn)定性理論的eN轉(zhuǎn)捩預(yù)測方法為例,作為轉(zhuǎn)捩判據(jù)的臨界N因子值選取的合理與否直接決定了轉(zhuǎn)捩預(yù)測精度。但是臨界N因子的確定受包括湍流度、噪聲水平等在內(nèi)的來流條件以及模型表面粗糙度等因素影響。相關(guān)參數(shù)的擾動可能會顯著降低臨界N因子的取值。這一現(xiàn)象在風(fēng)洞以及飛行試驗中都得到了觀察驗證[155]。 NASA利用設(shè)計的NLF超臨界機翼翼身體組合體構(gòu)型,在跨聲速風(fēng)洞進行臨界N因子值的標(biāo)定。其中TS波的臨界NTS因子值的標(biāo)定范圍在4~8之間變化[156],如圖42所示。Pecnik等[157]利用SC (Stochastic Collocation) 方法分析了來流條件不確定性和輸運形式轉(zhuǎn)捩模型參數(shù)不確定性對跨聲速燃氣輪機壓縮機葉片上層流-湍流轉(zhuǎn)捩預(yù)測精度的影響。研究結(jié)果表明,來流條件以及模型參數(shù)的不確定性對轉(zhuǎn)捩預(yù)測結(jié)果影響顯著,很大程度上解釋了確定性模擬與試驗值之間差異的原因。 圖42 不同狀態(tài)風(fēng)洞試驗與數(shù)值預(yù)測結(jié)果對比[156] 對于基于CFD技術(shù)的層流翼設(shè)計,不準(zhǔn)確的轉(zhuǎn)捩預(yù)測易造成過于保守或者過于激進的層流翼設(shè)計方案。同時存在偶然不確定性和認(rèn)知不確定性的混合不確定性問題,不確定性變量對設(shè)計得到的層流翼氣動性能的影響更為復(fù)雜。 確定性設(shè)計中的反設(shè)計方法難以有效實現(xiàn)層流翼的魯棒設(shè)計。一方面,給定的目標(biāo)壓力分布形態(tài)可能本身就是局部最優(yōu)解;另一方面,當(dāng)考慮來流湍流度、加工制造誤差、壁面缺陷、噪聲擾動以及穿云等不確定性影響因素時,很難保證給定的目標(biāo)壓力分布具有較好的氣動魯棒性。考慮不確定性影響的層流翼魯棒優(yōu)化設(shè)計方法及策略可在很大程度上解決相關(guān)設(shè)計問題。 Zhao等[158-159]采用非嵌入多項式混合展開(Polynomial Chaotic Expansion, PCE)對運營條件(巡航馬赫數(shù)Ma和升力系數(shù)CL)不確定性進行了分析,并將統(tǒng)計均值和標(biāo)準(zhǔn)差以線性加權(quán)形式引入NLF翼型的魯棒優(yōu)化中,提高了其氣動特性的魯棒性。Quagliarella等[160]采用MC方法研究了不同不確定性源對NLF超聲速公務(wù)機氣動特性的影響規(guī)律。運營條件不確定性(Ma、CL)對氣動特性的影響呈現(xiàn)一定的非線性特征。幾何不確定性中機翼前緣的形面擾動對氣動特性影響更為顯著。基于篩選的主要不確定性源,Quagliarella等[161]以風(fēng)險值和條件風(fēng)險值為度量形式進行了超音速NLF翼型魯棒設(shè)計,并利用Sobol指數(shù)揭示了對氣動性能影響最為顯著的幾何不確定性變量。Xiong等[162]針對層流短艙,利用非嵌入式PCE 方法和基于代理模型的全局優(yōu)化算法開展了考慮表面粗糙度影響的魯棒設(shè)計研究。 Hollom等[163-164]通過將eN方法的臨界N因子值視為不確定性變量,發(fā)展了一種可近似考慮由于來流湍流度,加工制造精度、前緣污染引起的表面粗糙度等不確定性因素對NLF翼型氣動特性影響的高效評估方法。這種評估方法假設(shè)轉(zhuǎn)捩位置變化不會對轉(zhuǎn)捩點前擾動波的發(fā)展產(chǎn)生影響,因此不確定性分析中無需對流場進行重新解算,顯著提高了計算效率。 針對具有28°前緣后掠角的NLF超臨界機翼,以臨界N因子值為不確定性變量,結(jié)合建立的不確定性分析方法,開展了層流翼魯棒優(yōu)化設(shè)計(DesignT),并與確定性優(yōu)化結(jié)果(DesignD)進行對比,如圖43所示[164]。相比確定性優(yōu)化設(shè)計,魯棒設(shè)計結(jié)果上翼面具有更小的吸力峰,峰值之后順壓梯度更大。同時外翼段轉(zhuǎn)捩提前了15%~20%當(dāng)?shù)叵议L。Hollom等[163-164]的研究指出對于考慮不確定性影響的層流翼氣動魯棒優(yōu)化問題,存在一個臨界閾值。當(dāng)作為轉(zhuǎn)捩判據(jù)的臨界N因子值大于該閾值,魯棒優(yōu)化可通過較小的統(tǒng)計均值意義下氣動性能的損失,獲得期望的魯棒性。但是,當(dāng)臨界N因子值明顯小于該閾值,那么為了實現(xiàn)相同的魯棒性,統(tǒng)計均值意義下層流翼的氣動性能將會顯著降低。 圖43 NLF機翼確定性優(yōu)化與考慮不確定性的魯棒優(yōu)化結(jié)果對比(實心圓點:轉(zhuǎn)捩點)[164] 類似的,DLR[165]也將線性穩(wěn)定性理論eN方法中TS和CF擾動波的臨界N因子值視為不確定性變量,如圖44所示。在針對具有大后掠、高雷諾數(shù)短程客機的NLF超臨界機翼氣動魯棒優(yōu)化設(shè)計中,進一步引入運營條件不確定性(來流馬赫數(shù)、升力系數(shù))。為了減小計算量采用了基于雙層代理模型的氣動魯棒優(yōu)化設(shè)計方法。其中,外層代理模型用于預(yù)測確定性變量對應(yīng)的性能函數(shù)值,內(nèi)層代理模型用于不確定性分析,計算性能函數(shù)的統(tǒng)計矩。圖45給出的轉(zhuǎn)捩位置隨臨界N因子值變化的云圖顯示,魯棒設(shè)計結(jié)果的轉(zhuǎn)捩位置變化較光滑,消除了確定性優(yōu)化結(jié)果層流區(qū)范圍階躍變化的現(xiàn)象。此外,研究結(jié)果指出,自然層流超臨界機翼統(tǒng)計平均意義下的層流區(qū)長度,呈現(xiàn)隨氣動魯棒性要求提高逐步減小的變化趨勢,如圖46所示。 圖44 魯棒優(yōu)化設(shè)計中假設(shè)的CF、TS波臨界N因子值可能的統(tǒng)計分布(A、B、C表示3種統(tǒng)計分布)[165] 圖45 確定性優(yōu)化與考慮臨界N因子值不確定性魯棒優(yōu)化的轉(zhuǎn)捩位置對比[165] 圖46 不同優(yōu)化設(shè)計結(jié)果壓力分布和轉(zhuǎn)捩位置隨優(yōu)化條件改變的變化對比(實心圓點:轉(zhuǎn)捩點)[165] 目前,針對層流翼的氣動魯棒優(yōu)化設(shè)計方法,均采用不確定性分析模型與非梯度算法相結(jié)合的實現(xiàn)方式。相關(guān)魯棒優(yōu)化設(shè)計研究涉及的不確定性變量個數(shù)通常不超過10個,確定性設(shè)計變量個數(shù)在百維以內(nèi)。相比層流翼確定性優(yōu)化問題,融入不確定性影響因素,引入基于統(tǒng)計矩信息的氣動穩(wěn)健性評價函數(shù),使得層流翼魯棒優(yōu)化問題的計算復(fù)雜度進一步成倍的增大。基于離散伴隨理論的梯度優(yōu)化方法具備的可高效處理具有大規(guī)模設(shè)計變量和約束優(yōu)化問題的能力,使其成為解決考慮多源不確定性影響的層流翼精細化魯棒優(yōu)化設(shè)計問題的重要技術(shù)途徑之一。但是還未見考慮不確定性影響,基于梯度優(yōu)化算法的層流翼氣動魯棒優(yōu)化設(shè)計的相關(guān)研究報道。此外,現(xiàn)有不確定性分析及魯棒設(shè)計主要圍繞自然層流機翼,鮮有針對混合層流機翼的相關(guān)研究。 針對面向噴氣式客機的層流減阻技術(shù),本文首先闡述了噴氣式客機的流動物理特征和復(fù)雜轉(zhuǎn)捩現(xiàn)象,指出NLF、HLFC的技術(shù)特點和適用范圍。然后回顧了國內(nèi)外NLF、HLFC技術(shù)的發(fā)展現(xiàn)狀。最后,從轉(zhuǎn)捩工程預(yù)測、優(yōu)化方法及設(shè)計理論方面,通過文獻綜述梳理了NLF、HLFC超臨界機翼氣動設(shè)計關(guān)鍵問題及發(fā)展趨勢。 1) 隨著對NLF技術(shù)研究的不斷深入,以及部分技術(shù)得到實際工程應(yīng)用,NLF機翼氣動設(shè)計技術(shù)研究重點逐步從轉(zhuǎn)捩機制相對單一的小后掠機翼或者百萬雷諾數(shù)量級的氣動部件,向流動現(xiàn)象復(fù)雜、多種轉(zhuǎn)捩機制并存的,高巡航馬赫數(shù)、千萬量級雷諾數(shù)的中等后掠機翼方向轉(zhuǎn)移。相關(guān)氣動設(shè)計理論及設(shè)計準(zhǔn)則有待進一步揭示。 2) 從最大化HLFC機翼綜合收益角度出發(fā),以較小的吸氣功耗、系統(tǒng)重量懲罰代價,顯著提升其氣動減阻收益是設(shè)計關(guān)鍵。HLFC技術(shù)呈現(xiàn)出的多學(xué)科屬性,使得降低甚至剔除功率消耗、系統(tǒng)重量懲罰代價,成為HLFC技術(shù)重要發(fā)展趨勢。 3) 可捕捉多種轉(zhuǎn)捩機制,適應(yīng)大規(guī)模并行計算的轉(zhuǎn)捩預(yù)測模型是發(fā)展層流翼高效設(shè)計方法的基石。未來全機一體化設(shè)計流場復(fù)雜,大規(guī)模并行計算是必然趨勢。 4) 面向全湍流氣動設(shè)計的非梯度類優(yōu)化方法和策略,原理上可推廣至層流翼的氣動優(yōu)化設(shè)計,具有互通性。但是,層流翼氣動優(yōu)化問題具有計算量更大,設(shè)計空間非線性特性更強,“維度災(zāi)難”現(xiàn)象更突出的特點。在面向全湍流氣動設(shè)計的非梯度類優(yōu)化方法發(fā)展趨勢基礎(chǔ)上,需結(jié)合層流翼優(yōu)化問題自身特點,改進、發(fā)展新的優(yōu)化方法及策略。此外,可引入人工智能、數(shù)據(jù)挖掘等新涌現(xiàn)的技術(shù)方法。 5) 面向全機的一體化設(shè)計是層流機翼氣動設(shè)計技術(shù)未來發(fā)展重要趨勢。發(fā)展基于離散伴隨的梯度優(yōu)化方法是解決層流翼“維度災(zāi)難”問題最具潛力的方法之一。梯度信息準(zhǔn)確、高效、魯棒求解,是耦合轉(zhuǎn)捩預(yù)測模型的層流翼梯度優(yōu)化方法需要解決的關(guān)鍵問題。對于設(shè)計空間非線性特性較強的層流翼優(yōu)化問題,梯度信息的不準(zhǔn)確求解會對梯類度算法的尋優(yōu)效果帶來極大的潛在挑戰(zhàn)。 6) 層流邊界層穩(wěn)定性對外界擾動的敏感性,使得相比全湍流氣動優(yōu)化問題,層流翼氣動設(shè)計問題對不確定性分析及魯棒設(shè)計的需求更為突出,成為重要發(fā)展趨勢之一。引入基于統(tǒng)計矩信息的氣動穩(wěn)健性評價函數(shù),使得層流翼魯棒優(yōu)化問題的計算復(fù)雜度成倍的增大。目前考慮不確定性影響的魯棒設(shè)計主要圍繞非梯度類優(yōu)化算法。融入不確定性影響因素,發(fā)展基于離散伴隨的梯度優(yōu)化方法,有望成為解決層流翼魯棒設(shè)計面臨的“維度災(zāi)難”問題的重要技術(shù)途徑之一。此外,多種認(rèn)知不確定性及偶然不確定性,對NLF/HLFC機翼氣動魯棒性的影響規(guī)律,以及層流超臨界機翼氣動魯棒設(shè)計準(zhǔn)則研究尚不完善,有待進一步揭示。


4 層流翼優(yōu)化設(shè)計
4.1 基于非梯度類算法的優(yōu)化設(shè)計



4.2 基于梯度類算法的優(yōu)化設(shè)計



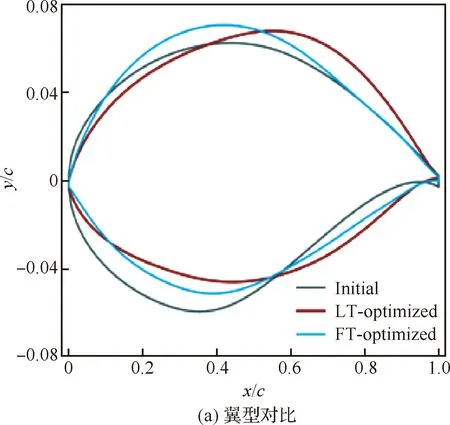
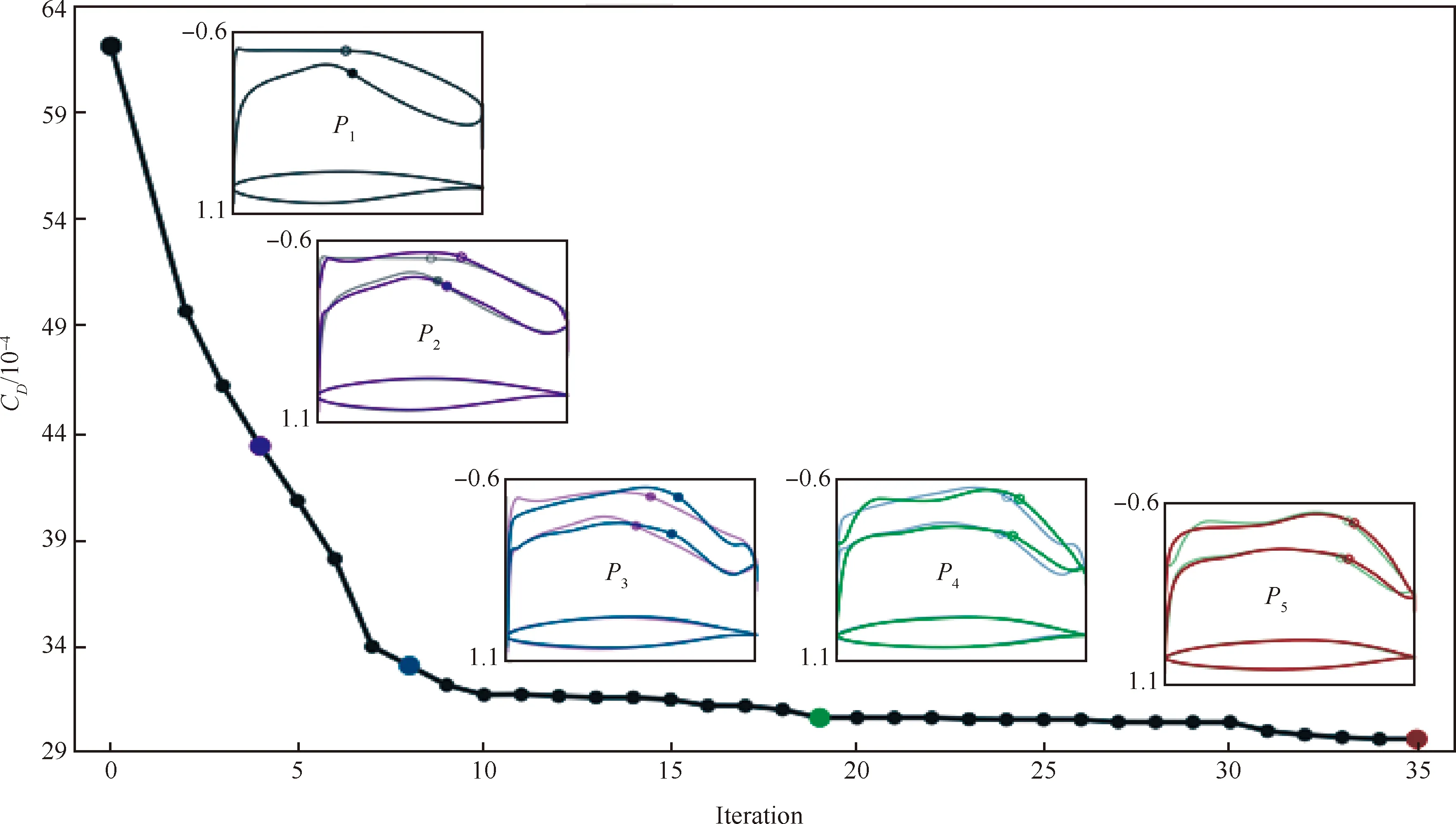

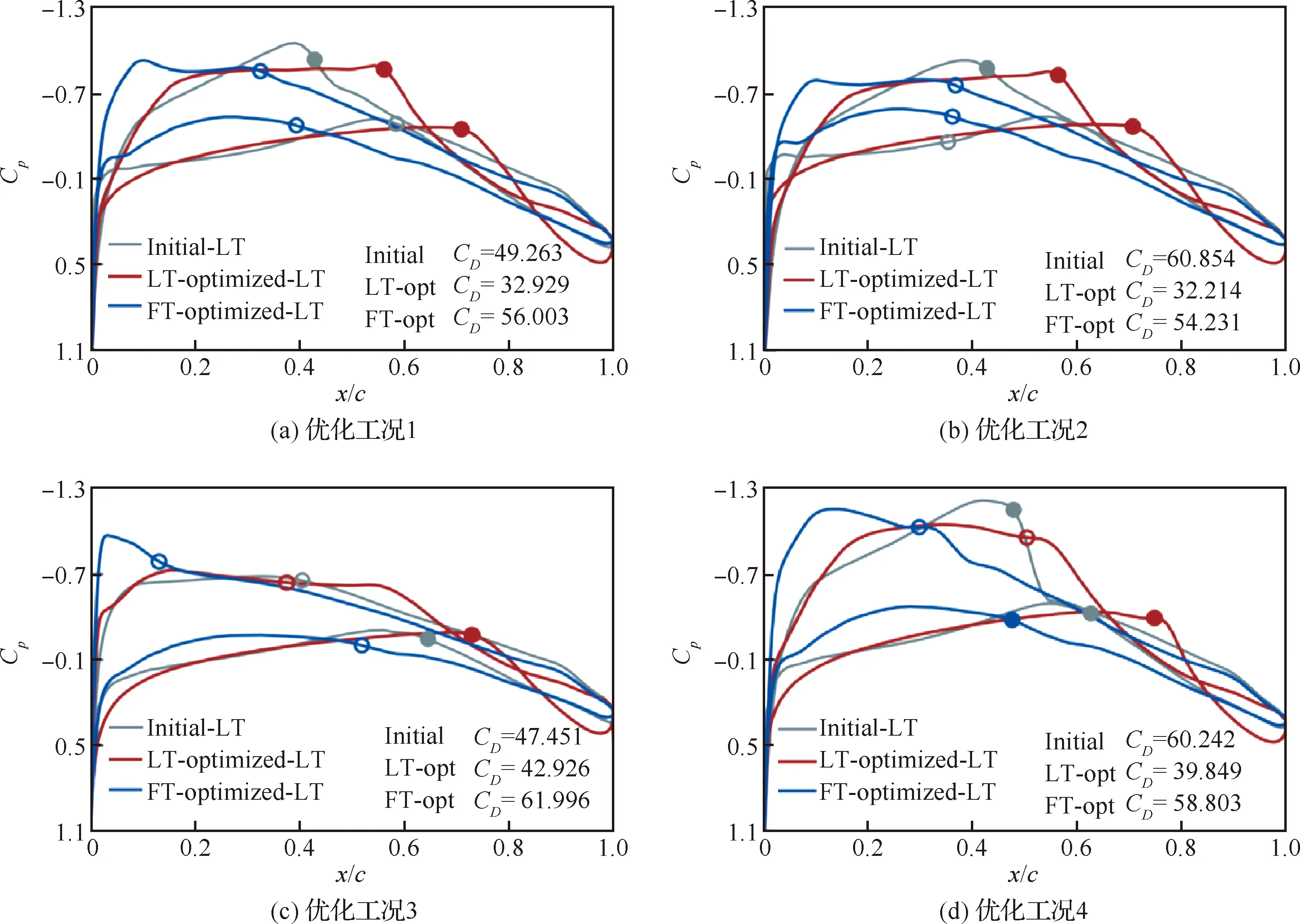

4.3 不確定性分析與魯棒設(shè)計

5 總結(jié)與展望

