自然層流飛行測試翼套的仿真和試驗

王浩，鐘敏，華俊，鐘海，楊體浩，王猛，雷國東

1. 中國航空研究院 技術研究二部，北京 100012

2. 中國飛行試驗研究院 中航工業飛行仿真航空科技重點實驗室，西安 710089

3. 西北工業大學 航空學院，西安 710072

4. 航空工業空氣動力研究院 高速高雷諾數航空科技重點實驗室，沈陽 110034

綠色發展已經成為航空業發展的趨勢和要求，國際航空運輸協會(The International Air Transport Association, IATA)在2020年初發布了《2050飛機技術路線圖》，概述和評估了未來可能的綠色航空技術，層流控制技術被認為是最有前景的技術之一，并有望達到較高的技術成熟度[1]。跟據對大量計算和飛行試驗的結果分析，摩擦阻力可占民機總阻力的50%，層流流動的摩擦阻力遠小于湍流流動，因而采用層流控制技術擴大層流區是減阻的一個重要途徑[2]。在層流邊界層控制的研究中，逐步形成了自然層流控制、全層流控制和混合層流控制等3種技術[3-4]，其中自然層流技術是一種被動控制技術，不需要引入額外的能量，適用于機翼后掠角較小的飛行器中。

針對層流控制技術的發展，國內外已經進行了大量的數值仿真研究，目前常用的轉捩預測方法有eN方法[5-7]，經驗關系式法[8]、低雷諾數湍流模型[9]和γ-Reθ t轉捩模型[10-12]，其中eN方法基于線性穩定性理論，著重于從物理上描述邊界層中小擾動TS(Tollmien-Schlichting)波沿流向的線性放大過程，并根據經驗選定判定轉捩發生的放大因子臨界值，可以預測低湍流度下沿流向的自然轉捩和分離流轉捩，在工程實踐中的應用較為廣泛。

在自然和混合層流機翼方面國外開展了大量的風洞和飛行試驗，并進行了一定的商業化嘗試。美國國家航空航天局和波音公司于2018年基于CRM(Common Research Model)標模分別在美國NTF(National Transonic Facility)風洞和歐洲ETW(European Transonic Wind Tunnel)風洞開展中等后掠角機翼的自然層流試驗，研究了不同雷諾數下TS波和CF(Cross Flow)波對轉捩的影響[13-14]。ATR(Avions de Transport Regional)公司和法國航空航天中心合作開展了未來支線飛機低阻層流機翼的試驗測試，在S1MA風洞中進行了雷諾數接近于真實飛行狀態的風洞試驗[15]。波音公司曾在B757飛機上開展了混合層流減阻研究[16]，NASA開展的SARGE(Subsonic Aircraft Roughness Glove Experiment)項目，在G-II飛機上進行了亞聲速飛機離散粗糙元翼套試驗研究[17-18]。歐盟在SAAB2000飛機的機翼上進行了混合層流翼套控制飛行試驗[19]，并在A320垂尾上進行了混合層流控制的飛行驗證[2]。空客在BLADE(Breakthrough Laminar Aircraft Demonstrator in Europe)項目中，采用A340作為載機，將外翼段替換為后掠角較小的自然層流機翼，評估大型客機上引入層流機翼技術的可行性。Honda Jet輕型公務機采用自然層流機翼，在2003年進行了首飛，達到了預期的設計目標[20-21]。國內張彥軍[22]、艾夢琪[23]等開展了一系列風洞試驗研究，但國內之前尚未開展層流機翼的飛行試驗，對相關數據的對比分析研究也較為罕見，特別是缺少對仿真、風洞試驗和飛行試驗三者間的對比分析。

近期，國內層流翼套飛行測試團隊進行了自然和混合層流機翼翼套的設計、數值仿真、風洞試驗、飛機改裝和飛行試驗的相關探索并陸續發表有關研究內容[24-26]，數值仿真可以為試驗研究提供預評估結果。本文主要針對該項目中的自然層流機翼翼套的數值仿真、風洞試驗和飛行試驗的結果開展對比分析，并且通過數值分析結果與試驗結果、特別是中國首次自主開展的層流飛行實測數據的對比和數據相關性分析，驗證本項目的數值方法，為今后開展自然層流機翼的仿真、設計和試驗研究及工程化開發提供參考。

1 飛行試驗機、風洞試驗模型和數值仿真方法

1.1 飛行試驗機和風洞試驗模型

飛行試驗使用了某小型民用飛機作為原型機，為直線型下單翼，后掠式垂直尾翼帶大背鰭，發動機安裝形式為尾吊，便于翼套的安裝和轉捩的測量。在原型機的單側機翼上安裝自然層流翼套，翼套的設計基本保持兩側機翼載荷的平衡。加裝翼套的層流機翼翼套飛行試驗機半模如圖1所示，翼套的控制面位于展向3.36 m和展向4.36 m，翼套展向長度為1 m，展向3.36 m位置處的弦長為2.37 m，展向4.46 m位置處的弦長為2.12 m，相較原始機翼前伸0.25 m；過渡段的兩個控制剖面分別位于2.91 m和4.69 m，內過渡段長度為0.45 m，外過渡段長度為0.33 m，翼套與過渡段的長度之和為1.78 m，約占半展長的21%。翼套后掠角與機翼外翼段后掠角一致均為5度，試驗中翼套的當地雷諾數約為12×106～18×106，轉捩主要受TS波擾動造成，橫流的影響較小。

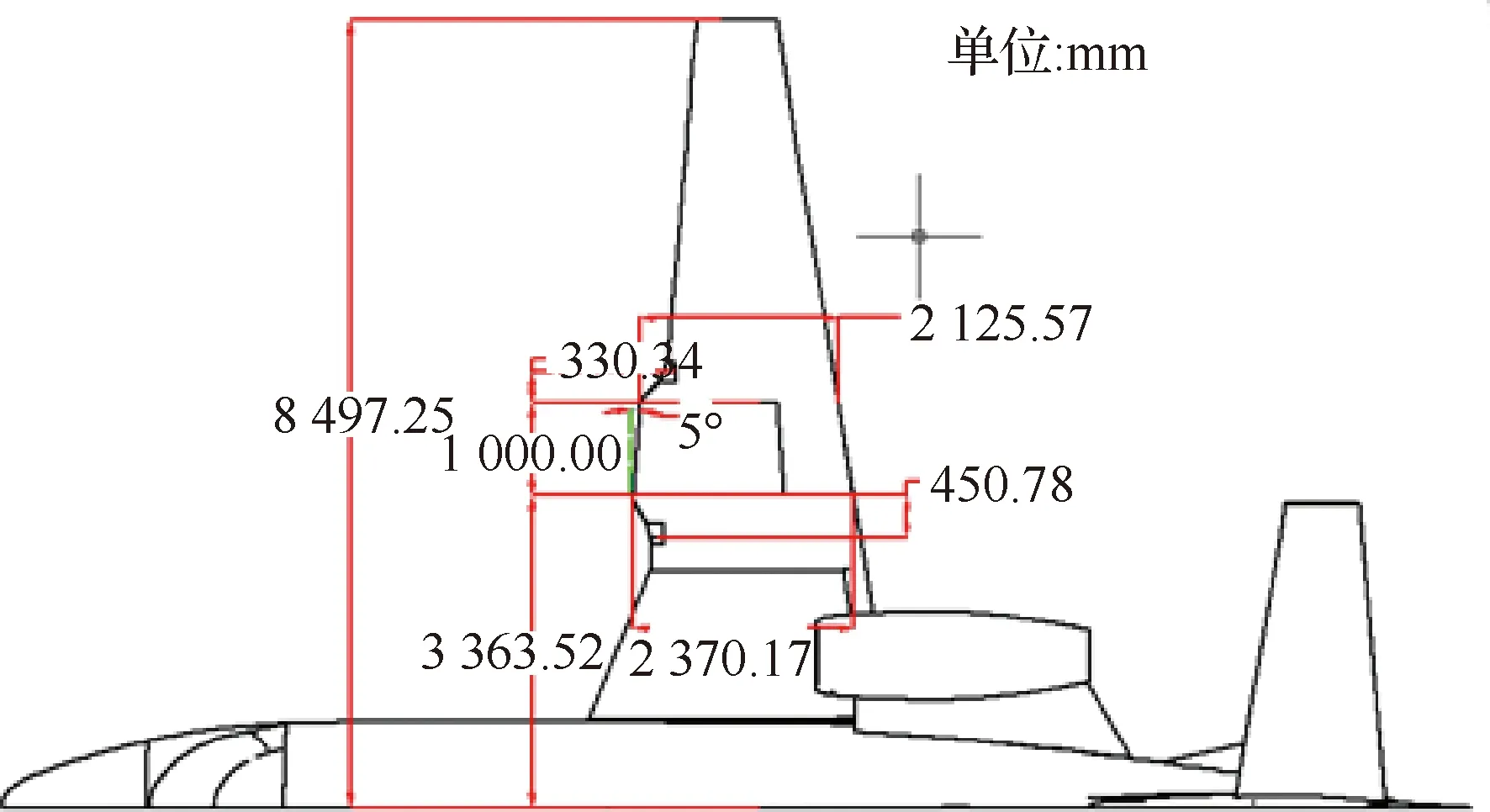
圖1 自然層流機翼翼套飛行試驗機

層流機翼翼套采用復合材料加工，通過紅外熱成像的方式進行邊界層轉捩的測量，試驗過程中通過表面加熱的方式獲得機翼上表面質量較高的紅外熱圖[25]。飛行測試翼套如圖2所示。

圖2 自然層流機翼翼套測試區域

在展向3.623 m位置處從前緣至60%當地弦長布置19個測壓點，記為S3測壓剖面；在展向4.303 m處從前緣至60%當地弦長布置18個測壓點，記為S2測壓剖面；考慮到測壓孔的擾動會引起轉捩，在S3測壓剖面從16.2%當地弦長到60%當地弦長沿斜向與S3剖面成18°角布置了9個測壓點，記為S1測壓剖面。由于更換混合層流控制的吸氣前緣所需，層流翼套在18%當地弦長處，存在一條接縫，通過手工處理使其表面粗糙度和波紋度盡量滿足自然層流的要求。根據試驗機的大氣數據系統測量所得，自然層流機翼翼套飛行試驗的部分典型工況如表1所示。

表1 自然層流機翼翼套飛行試驗典型工況

在飛行試驗前，截取翼套中間部位翼型開展了風洞試驗研究，風洞試驗模型機翼翼型與自然層流翼套S2和S3測壓剖面翼型的對比如圖3所示(為便于對比，厚度方向有放大)，為適應機翼扭轉角，內側的S3測壓剖面的當地攻角略大于外側的S2測壓剖面。設計加工了簡單后掠機翼的風洞試驗模型(圖4)。

圖3 自然層流機翼翼套翼型

圖4 自然層流機翼翼套風洞試驗模型

風動試驗模型機翼展長為900 mm，弦長為300 mm，前緣后掠角為5°。為與飛行試驗和仿真結果更好的進行對比，在展向450、600、750 mm 處分別沿斜向與機身軸線成18°角布置測壓孔。該模型在FL-3風洞開展了自然層流風洞試驗，在內外測壓剖面之間的區域采用紅外熱圖的方式進行轉捩測量，風洞試驗工況如表2所示。

表2 自然層流機翼翼套風洞試驗工況

1.2 數值仿真方法

數值仿真流程采用的計算流體力學(CFD)求解器為中國航空研究院的雷諾平均Navier-Stokes (RANS)求解器AVICFD-Y，采用的湍流模型為SST。

進行轉捩分析時采用的是基于線性穩定性理論的eN方法，結合CFD求解器得到的機翼截面幾何信息、壓力信息、當地后掠角、馬赫數(Ma)、雷諾數，基于錐形流假設，求解層流邊界層方程，獲得邊界層的基本解[27]，進而求解四階可壓縮Orr-Sommerfeld方程進行穩定性分析，求解得到擾動放大因子(N)，當N達到經驗所得的轉捩閾值(Ncr)時可以認為發生轉捩，從而獲得轉捩位置，計算中風洞試驗的Ncr定為6.5，而飛行試驗的Ncr定為10；將求解得到的轉捩信息通過強制給定轉捩位置的方式代回到CFD求解器中，重新進行流場計算獲得壓力信息，并重新進行轉捩分析獲得新的轉捩位置，直到轉捩位置的變化滿足收斂條件為止[6]。計算流程如圖5所示。

圖5 計算流程圖

數值計算采用結構網格，飛行試驗機網格節點數為1 000萬，邊界層內第一層網格高度為0.000 001 m，增長率為1.15，機翼沿弦向一周的網格節點數為201，飛行試驗機的計算模型網格如圖6所示；風洞試驗模型網格節點數為400萬，邊界層內第一層網格高度為0.000 002 m，增長率為1.2，機翼沿弦向一周的網格節點數為265，風洞試驗模型的計算模型網格如圖7所示。計算狀態以翼套的設計狀態馬赫數0.6，攻角0°為主，兼顧其他試驗和飛行狀態。

圖6 飛行試驗機計算模型網格

圖7 風洞試驗模型計算模型網格

2 數值仿真和風洞試驗結果對比

2.1 壓力系數分布

機翼各截面數值仿真與風洞試驗的壓力系數(Cp)分布對比如圖8和圖9所示，其中Pt為總壓，風洞測壓結果與數值仿真的一致性較好。

圖8 Pt=0.1 MPa、Ma=0.6時機翼截面壓力系數分布

圖9 Pt=0.2 MPa、Ma=0.6時機翼截面壓力分布

2.2 轉捩位置

風洞試驗經過處理可以得到規整的紅外熱圖，利用梯度算法計算熱圖的灰度梯度場，并計算弦向和展向的合成梯度絕對值，利用梯度最大值判斷每個展向剖面的轉捩位置，得到一組轉捩點站位數據。利用統計方法得到這些轉捩點站位在整個弦向坐標(0～1.0)內的概率密度分布曲線，根據最大概率密度指示轉捩位置。根據數值仿真分析的結果，在中間翼段沿展向轉捩點的弦向位置變化不大，以y=600 mm的截面為例，對比不同狀態時數值仿真和風洞試驗機翼轉捩位置(xtr/c)隨攻角的變化曲線，如圖10所示。各種工況下，在小攻角和大攻角時，轉捩位置隨攻角變化較小，數值仿真得到的轉捩位置較風洞試驗結果靠前，更接近翼套設計轉捩位置。該仿真方法在風洞狀態小雷諾數時會得到層流分離泡，從而轉捩預測結果較風洞試驗靠前。隨著攻角的增大，從某個攻角開始轉捩位置會迅速前移，數值仿真得到的轉捩位置開始迅速前移的攻角較風洞試驗結果更大。對比不同風洞總壓即不同雷諾數時的結果，可以發現當總壓即雷諾數增大后，在較小攻角時風洞試驗測得的轉捩位置就開始較為顯著的隨攻角增大而前移，在0°攻角時已前于飛行雷諾數的設計轉捩位置。風洞試驗和數值仿真兩者轉捩位置變化的趨勢存在一定差異，原因可能為轉捩位置對風洞品質、表面質量等因素較為敏感，導致風洞試驗中的轉捩位置較仿真結果在更小的攻角時即發生前移，增壓后風洞品質進一步的變化促使轉捩位置前移的攻角進一步減小，目前仿真分析方法尚無法對暫沖式增壓風洞紊流度進行準確的模擬。后續對紅外熱圖的分析也可以得到類似結論，有必要進一步進行研究確認。

圖10 轉捩位置隨攻角的變化曲線

對比Ma=0.6、攻角=0°時不同總壓風洞試驗得到的紅外熱圖與數值仿真得到的摩阻云圖，如圖11所示，不同總壓下仿真得到的轉捩位置基本一致，且沿展向基本無變化。對于風洞試驗得到的紅外熱圖，機翼表面存在較多湍流楔，主要為模型表面測壓孔和灰塵等引起，在總壓為0.1 MPa 時可以觀察到明確的轉捩線，獲得可靠的轉捩位置；在增壓至0.2 MPa時機翼表面湍流楔迅速增多，推斷此時試驗測得的轉捩位置較早前移可能與風洞增壓后品質改變有關，有待進一步研究確認。

圖11 風洞試驗紅外熱圖與數值仿真摩阻系數云圖對比

3 數值仿真和飛行試驗結果對比

3.1 壓力系數分布

飛行試驗中飛行器的氣動力需要通過換算得出，因此通過對比壓力系數分布可以更好的保證數值仿真與飛行試驗狀態的一致性，但飛行試驗中壓力系數分布的獲取需要確定更為準確的參考靜壓。試驗過程中在機身最大截面處側面舷窗開孔測量的機身靜壓和機頭處空速管測量的機頭靜壓，作為對翼套壓力數據進行無量綱化的參考壓力，同時根據飛行試驗機的大氣數據系統測得的氣壓高度結果可以求得相應的理論靜壓，也可以作為參考壓力。幾種不同參考壓力的對比如表3所示,Ma=0.6、攻角=0°時機身靜壓與理論靜壓較為接近，但Ma=0.46，攻角=2°時機身靜壓減小較為明顯；機頭靜壓在攻角變化時相對穩定，顯著大于機身靜壓和理論靜壓。

表3 不同方法得到的參考壓力

以外側的S2測壓剖面為例，對比不同靜壓值作為參考壓力時仿真和飛行試驗的壓力系數分布，如圖12和圖13所示，其中H表示飛行高度。在Ma=0.6，攻角=0°的設計狀態下，機身靜壓和理論靜壓作為參考壓力，數值仿真和飛行試驗的壓力系數分布均可以取得較好的一致性，采用機頭靜壓作為參考壓力時，仿真和飛行試驗的壓力系數分布差異較大。當Ma減小到0.46，攻角增大為2°時，相較于機頭靜壓和機身靜壓，理論靜壓作為參考壓力時飛行試驗和數值仿真的壓力系數分布的一致性更好。仿真與飛行試驗的攻角差值約為0.3°。

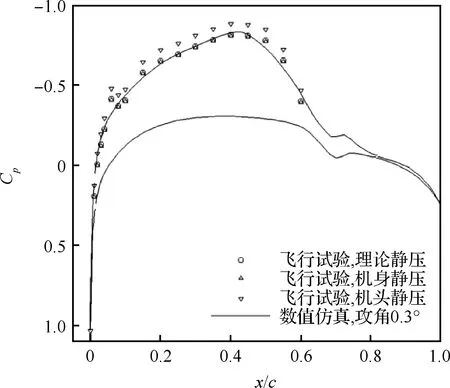
圖12 H=7 000 m、Ma=0.60、攻角=0°時數值仿真與飛行試驗S2截面壓力系數分布

3.2 轉捩位置

以H=7 000 m、Ma=0.60、攻角=0°，H=7 000 m、Ma=0.46、攻角=2°和H=6 000 m、Ma=0.60、攻角=0°的狀態為例，飛行試驗機翼上表面紅外熱圖(左)和數值仿真摩阻系數云圖(右)的對比如圖14所示。兩圖中黑點及虛線從前緣向后分別標記0.05、0.16、0.20、0.25、0.30、0.35、0.40和0.45倍當地弦長的位置，紅外熱圖中藍色實線標識出飛行試驗測量得到的轉捩位置。可以發現，在Ma=0.6，攻角=0°的設計狀態，飛行中S2、S3截面前緣處的測壓孔誘導出兩個湍流楔，在湍流楔的影響區域之間存在大范圍的層流區，此時仿真結果和試驗結果一致性很好，轉捩均發生在約0.45倍弦長位置附近；在Ma=0.46，攻角=2°的非設計狀態，轉捩發生在接縫之前，此時仿真結果和飛行試驗結果也較為接近。對于圖14(c) 所示的設計馬赫數和攻角，當飛行高度降低為6 000 m時，雷諾數增大到17.8×106，此時層流機翼翼套仍然可以保持0.45倍弦長左右的層流區，同時也進一步說明暫沖式風洞在增壓時的流場品質對轉捩位置測量具有一定影響。

圖14 飛行試驗紅外熱圖與數值仿真摩阻系數云圖對比

選取翼套展向y=3.932 m位置的中間截面記為T1截面，如圖14(b)右圖所示，分析其擾動放大因子的變化過程，不同狀態時的結果如圖15所示。對應不同高度即不同雷諾數，Ma=0.6，攻角=0°的設計狀態下，受較大的順壓梯度的影響，TS波擾動放大因子(NTS)增長均較慢，直到0.45倍弦長之后，較大的逆壓梯度才導致其迅速增長引發轉捩；此時在上翼面順壓區NTS均較小，多處于2以下。在馬赫數0.46，攻角=2°時(圖15(b))，在前緣附近NTS即迅速增長導致在接縫前發生轉捩，穩定性分析的結果與飛行測量也有很好的一致性。結合圖12～圖15結果進行分析，攻角=0°時順壓較為顯著，此時擾動的放大速度較慢，故圖14(a)和圖14(c)中翼套上表面沿展向均在45%弦長附近發生轉捩；攻角=2°時順壓梯度較小，此時擾動的放大速度較快，轉捩對壓力分布較為敏感，因此圖14(b)中數值仿真得到的翼套上表面轉捩位置會沿展向變化。

圖15 T1截面NTS變化過程

3.3 截面阻力

選取部分自然層流區較長的飛行試驗狀態，在T1截面后方布置尾流耙測量截面阻力，分別進行自然轉捩和6%弦長處強制轉捩的飛行試驗，研究自然轉捩技術的減阻效果，涉及的飛行試驗狀態如表4所示。

表4 截面阻力系數測量飛行試驗工況

根據數值仿真結果進行分析時，考慮到翼套僅對上翼面進行了特殊處理，進行紅外測量，因此僅在翼套上翼面進行自然轉捩分析，其余部分均按照全湍進行處理。采用尾跡動量損失積分法計算阻力，阻力系數計算公式為

(1)

式中：c為截面弦長；Cf為尾跡截面單位長度上的無量綱動量損失，具體可以參考文獻[28]。為與飛行試驗保持一致，在截面后方0.12倍弦長的位置截取數據求解截面阻力，數值仿真結果與飛行試驗結果的對比如表5所示。從表中可以看出，同樣狀態時，數值仿真的自然轉捩和強制轉捩的截面阻力系數差值在0.001 2～0.001 6之間，飛行試驗結果在0.001 3～0.001 6之間，二者結果一致性很好，差別約為0～0.000 2。

表5 飛行試驗與數值仿真截面阻力系數減小量

4 結 論

1) 建立了自然層流機翼數值仿真的CFD-流動穩定性分析流程，針對自然層流機翼翼套飛行試驗機和縮比風洞試驗模型開展了設計驗證和典型試驗狀態仿真，多數狀態下數值仿真和風洞試驗的壓力系數分布具有較好的一致性，和飛行試驗壓力分布的對比取得了更好的一致性。

2) 研究中發現，風洞總壓為0.1 MPa時，雷諾數為300萬量級，數值仿真得到的轉捩位置隨攻角的變化規律與風洞試驗結果一致，轉捩位置相對風洞試驗靠前，更接近翼套的設計轉捩位置；風洞增壓為0.2 MPa時，雷諾數增大為600萬量級，風洞來流紊流度也隨之增大，機翼表面出現大量的湍流楔，影響了風洞試驗對轉捩位置的測量。

3) 對于飛行測試的壓力分布，對比了不同參考靜壓源的結果：相較于機頭處靜壓和機身最大截面處靜壓，飛行試驗機大氣數據系統測量的氣壓高度對應的理論靜壓作為參考壓力時得到的壓力系數分布與數值仿真結果更為一致，作為對比數據更為合理，此時數值仿真得到的壓力系數分布和飛行試驗結果具有良好的一致性。

4) 在翼套設計馬赫數0.6，攻角0°附近，數值仿真得到的轉捩位置和飛行試驗結果高度一致；在雷諾數達到1 800萬量級時機翼上翼面也可以實現45%左右的層流區；在較低的馬赫數較大攻角時，仿真預測的轉捩發生在接縫之前，也與飛行測試重合良好。

5) 同樣狀態下數值仿真計算得到的采用層流技術帶來的截面阻力減小量與飛行測量結果基本一致，兩者差別在0～0.000 2之間。