重慶市梁灘河匯流閾值分析與地貌發育研究
胡煜佳,鄭莉萍,張森林,邵景安,2
(1.重慶師范大學地理與旅游學院,重慶 401331;2.三峽庫區地表過程與環境遙感重慶市重點實驗室,重慶 401331)
0 引 言
隨著GIS技術的不斷發展以及在水文模擬中的廣泛應用,對流域河網的提取大體分為兩種思路:一種是基于已有的遙感影像進行自動提取;另一種則是利用DEM數據進行提取[1]。以DEM和ArcGIS為載體進行河網數字化、自動化提取是眾多研究者采取的方法之一;而河網提取以及水文特征信息獲取的關鍵在于每個格網單元的匯流累積量。匯流累積量取決于每個格網單元的流向以及流量分配[2],采取不同計算流向的方法以及匯流閾值的擬定其自動提取的河網和流域水文特征也不一。單流向算法和多流向算法是研究中常見的兩種流向算法[3],單流向算法如D8算法[4-5]、Lea算法[6]、Rho8算法[7]等;而多流向算法則認為水流具有分散性,分散流入其他下游格網單元[8],例如FD8算法[9]、Dinf算法[5]等。針對匯流閾值的擬定,學者也采取了不同方法進行研究。左穎等[10]采取多閾值約束法、單一t值確定法、河網密度法綜合確定合理閾值;唐杰等[11]采用河網和河源密度法確定集水面積閾值,函數曲線的拐點則為最佳集水面積閾值;張曉嬌等[12]采用河網密度法和水系分形法綜合確定閾值;許斌等[13]結合分形理論分析了不同匯流累積閾值下河網分形維數和密度變化率特征。綜上可看出,大部分學者確定匯流閾值采用頻率較高的是河網密度法,并且都用多種方法綜合確定。由于基于DEM數字高程模型提取河網以及流域水文信息可行性高、易于操作。因此,本文選取了重慶市污染情況最復雜的次級河流之一——梁灘河流域,基于研究區12.5 m分辨率的DEM,以ArcGIS軟件為平臺提取流域水文信息,運用數理方法確定最佳閾值,最終提取的河網與TM影像的歸一化水體指數提取的河網與三調數據成果提取的河網進行對比分析,并運用Horton算法與起伏比法對流域地貌發育階段進行識別判定。
1 研究區域概況
梁灘河流域位于重慶主城區縉云山與中梁山之間的北碚丘陵谷地及中梁山的狹長槽谷地帶,地貌分區為川東平行嶺谷區,地勢北低南高,東西高中間凹。該河流發源于九龍坡區走馬鎮廖家溝水庫,流經九龍坡、沙坪壩區、北碚3區,最后匯入嘉陵江,是嘉陵江下游右岸的一條主要支流、主城區流域面積第三大的次級支流,整條流域共有55條支流,干流長約88.7 km,流域面積516.18 km2。流域內常住人口超過20萬,并且由于梁灘河流域內曾經發展的養殖業和小型加工業興盛,其水質受農業活動、工業、城鎮污水的影響較大,是全市污染情況最復雜、治理難度最大的次級河流之一。因此,選取該流域為研究對象,提取河網等河流水文信息以期為研究該流域范圍內的農業面源污染或水質評價奠定基礎。其DEM影像見圖1。
2 數據來源與預處理
本文所用的DEM數據來源于重慶市生態環境大數據應用中心,其分辨率為12.5 m,根據梁灘河流域邊界對其進行裁剪處理。由于原始DEM存在凹陷單元格以及在平坦地區的水流方向存在不確定性;因此需對原始DEM進行預處理。即填洼操作,削峰填低,創建無凹陷DEM。這是進行流域水文分析的基礎。在填洼過程中,限制值Z為指定凹陷點深度和傾瀉點間的最大允許差值并確定要填充的凹陷點和保持不變的凹陷點,由于Z值無法精確限定,在本次操作過程中未對Z限制作出任何指定,因此將移除所有峰值。本文所用第三次國土調查(以下簡稱“三調”)數據來源于重慶市國土局。TM影像來源于地理空間數據云,其分辨率為30 m,利用ENVI5.3對影像進行拼接、大氣校正、輻射定標、裁剪等預處理。
3 流域水文特征信息提取
3.1 流域水文特征信息提取
3.1.1 水流方向的確定
在對原始的DEM進行填洼操作后,需要確定每個柵格單元的水流方向,而流向判斷主要分為單流向算法和多流向算法[14]。單流向算法目前應用最廣泛的則是D8算法。該算法將水流方向簡化為8個方向,即東北、東、東南、南、西南、西、西北和北被定義為有效的水流方向,分別用128、1、2、4、8、16、32、64這8個有效特征碼表示;再根據高程值從而決定其每個柵格的水流方向[4]。多流向算法如FD8算法[9]、Dinf算法[5]等。本文利用ArcGIS10.2中D8算法計算水流方向,但此時要檢驗填洼是否完全;若不完全,則需反復填洼。
3.1.2 匯流累積量的計算
每個柵格都會產生一定的水流方向,某一柵格的匯流累積量就意味著從上游流至該柵格的流量累計;因此,通過計算匯流累積量從而判斷每個柵格的匯流能力。匯流累積量為柵格單元數目與柵格單元面積乘積之和[1]。
3.1.3 河網提取與分級
河網提取是在計算匯流累積量的基礎上進行的。即,將匯流累積量大于某一設定閾值的柵格提取出來的便是河網;因此,閾值擬定對最終提取河網尤為關鍵。隨后再利用水文分析工具集下的Strahler河網分級法進行分級。
3.1.4 柵格河網矢量化與水文特征信息提取
利用水文分析工具集下的柵格河網矢量化工具,將表示線狀網絡的柵格轉換為表示線狀網絡的要素;再使用河流鏈接、分水嶺工具生成集水區;最后,利用轉換工具集下的柵格轉面工具將柵格數據集轉換為面要素,從而計算不同閾值下的流域面積、河流長度、河道個數等水文信息。
3.2 TM影像的流域水文信息提取
利用遙感影像提取流域水體信息的方法主要有目視解譯和計算機自動解譯2種[15]。本文利用常用的水體信息提取方法——歸一化水體指數(NDWI)進行自動提取。該方法由Mcfeeters[16]在NDWI的基礎上提出,利用不同波段對地物反射的特征——近紅外波段對水體的強吸收而植被強反射的特點,采用綠波段和近紅外波段的比值可以較大程度上抑制植被信息,突出水體,從而較好地提取流域水體(見圖2)。這里歸一化水體指數
NDWI=(Green-NIR)/(Green+NIR)
(1)
式中,Green為綠光波段反射率;NIR為近紅外波段反射率。
從圖2可看出,利用ENVI對TM影像的波段識別最終得出水體歸一化處理效果不是很理想,對河流以及小面積水域提取效果不佳或存在漏提或斷流現象,導致諸類現象的原因可能是該遙感影像分辨率不高,對于地物的識別較模糊,有待采用更高分辨率的遙感影像進行提取與研究。
4 結果與分析
4.1 匯流閾值對流域水文特征的影響
閾值直接影響河網的生成以及流域水文信息,不同匯流閾值條件下其提取出來的河流長度、流域面積、河道個數等有所差異。圖3顯示,隨著匯流閾值的增大河網越稀疏,支流數量越少。
通過屬性表計算出不同匯流閾值下的河流長度、流域面積、河網密度以及河道個數(見表1)。
由表1可知,當匯流閾值由10 000增加至30 000時,河道個數由200個減至60個,減少了70%,河流長度、流域面積、河網密度分別降低了46.72%、3.42%、44.83%;當匯流閾值由30 000增加至50 000時,河道個數、河流長度、流域面積、河網密度分別降低了48.33%、25.87%、1.53%、24.72%;當匯流閾值由50 000增加至80 000時,河道個數由31個減至20個,減少了35.48%,其余分別降低了18.29%、1.85%、16.75%;匯流閾值由80 000增加至100 000時,河道個數由20個減至13個,減少了35%,其余分別降低了9.76%、2.7%、7.25%。由以上分析可知,隨著匯流閾值的增加流域各水文特征值都在不斷降低,但是變幅最小的為流域面積,其他3類特征值波動明顯,并且可發現匯流閾值由10 000增加至30 000 時流域各水文特征值變化最為明顯,各特征值急劇減小;閾值大于30 000后,各水文特征值變化幅度明顯減小。
由于流域面積受閾值波動影響遠小于其他特征值,因此,本文分別用對數、冪函數、指數函數、多項式函數等函數對匯流累積量與河流長度、河網密度、河道個數進行趨勢分析,尋找最佳函數類型以及最佳閾值,經過多次實驗發現冪函數擬合性最優。匯流閾值與河流長度、河網密度、河道個數的冪函數關系如下:
Y1=55 755.948X-0.562(R2=0.997 4)
(2)
Y2=74.479X-0.527(R2=0.995 1)
(3)
Y3=6.909X-1.134(R2=0.998 8)
(4)
式中,Y1為河流長度,km;Y2為河網密度,km/km2;Y3為河道個數;X為匯流閾值;R2為擬合度。
對匯流閾值與河流長度、河網密度、河道個數的冪函數關系求二階導數,并做非線性擬合與趨勢分析(見圖4)。
由圖4可看出,河流長度、河網密度、河道個數隨閾值變化的二階導數趨勢一致,曲線的變化趨勢由急劇下降至緩慢減少再至趨于平緩,都是從10 000 增至20 000時,流域各水文特征值急劇下降,20 000增至30 000時,各特征值降幅減小但降幅也較其他值段明顯。因此,閾值30 000左右是該流域明顯的一個特殊點。匯流閾值與河流長度、河網密度、河道個數的二階導數關系曲線趨于平緩時所對應的點為合理的匯流閾值。從圖4還可看出,當閾值在35 000時為曲線趨于平緩時的變點,其二階導數值趨向0,各特征值趨于穩定,后與實際河網進行對比驗證。即
(5)
(6)
(7)
4.2 提取河網結果的分析
通過最佳匯流閾值提取的河網需要檢驗與實際河網的差距。本文以三調數據成果提取的河流作驗證分析(見圖5),發現通過數理方法確定的最佳匯流閾值35 000提取的河網(見圖6)與實際河網較為接近,但仍有一定出入;從DEM中提取的河網很好地保留了河流主干道信息,但存在有一小部分支流不能很好地體現或存在“偽支流”現象,尤其是流域中西部存在部分偽河道。通過其他閾值提取的河網發現,當閾值低于35 000時,河網越密集,提取的河網發育較好,設定的閾值較小時生成的河網與實際河網對比發現很多都是“偽支流”,在實際中并非真正的河網。當閾值高于35 000時,河流長度變短,雖然都較好地保留了主干道信息,但絕大部分支流無法體現,支流發育程度較差,與實際情況也不符合。綜上所述,該研究區最佳匯流閾值為35 000,提取的河網在保留河流主干道信息之外其支流也能較好地與實際河網吻合。
4.3 地貌發育階段識別
4.3.1 Horton算法
Horton算法是依據地形圖或數字高程數據利用ArcGIS提取水系,再用Strahler河網分級法對水系進行分級[17]。即
RB=NW-1/NW
(8)
RL=LW/LW-1
(9)
(10)
式中,RB為水系分叉比;RL為河長比;w為水系級別號;NW為第w級河道數目;LW為第w級河道的平均長度;Db為Horton-Strahler水系分維值。
由上述表達式得出梁灘河水系分維值為1.072 4,根據王玉成等[18]和任娟等[19]的相關研究,提出當水系分維值Db≤1.6、1.6 4.3.2 起伏比法 判斷地貌發育階段的方法除了Horton法,還有經典的起伏比法,該方法由Pike和Wilson通過數學方法推導出的估算面積高程積分值的典型方法,其計算過程方便快捷、精度也較高[17]。計算式為 HI=(Hmean-Hmin)/(Hmax-Hmin) (11) 式中,HI為流域的起伏比;Hmean為流域的平均高程,m;Hmax為流域的最大高程,m;Hmin為流域的最小高程,m。 依據地貌發育理論與Strahler對地貌發育階段的定量劃分(見表2)。梁灘河流域HI值為0.514 9,處于地貌發育階段的壯年(偏幼)期。由以上2種方法可推斷出,梁灘河流域的地貌發育階段可能為幼齡期向壯年(偏幼)期發展。 表2 地貌發育階段劃分標準 目前,利用DEM和ArcGIS快速提取流域河網的方法廣泛適用于各個流域的水文分析,是眾多研究者采取的主要方法。本文以重慶市梁灘河為例,利用ArcGIS10.2水文分析模塊的相關工具提取河網等水文信息,并通過數理方法確定最佳匯流閾值與流域地貌發育階段判定,得出了以下結論。 (1)隨著匯流閾值的增大,河流長度、流域面積、河網密度、河道個數等流域水文特征值不斷減小,提取的河網越稀疏,支流數量越少。 (2)根據匯流閾值與河流長度、河網密度、河道個數的二階導數關系曲線確定其最佳匯流閾值為35 000。 (3)通過匯流閾值35 000提取的河網與TM影像的水體歸一化處理結果、三調數據成果提取的河網進行對比發現該結果具有可靠性,但仍有一定出入。筆者認為原因可能如下:①在使用軟件計算與提取的過程中,由于算法的局限性以及某些參數的設定不同,會對運算結果產生很大的影響,如在填洼中Z值的限定、計算流量中匯流閾值的擬定都會對最后提取的結果產生很大的影響,眾多學者尤其對于Z值的限定無法做出較好的回答,這便成為日后研究中所需關注的一大重點;②利用TM影像進行水體歸一化處理效果并不太理想,存在漏提或斷流現象。這可能是由于TM遙感影像分辨率不高,因此有待采用更高分辨率的遙感影像進行提取與研究。 (4)針對梁灘河流域地貌發育階段的識別,本文通過Horton算法與起伏比法,最終推斷出該流域地貌發育階段可能為幼齡期向壯年(偏幼)期發展。 就總體而言,在流域提取或水文分析中越來越廣泛運用GIS技術,相關理論研究和提取方法也日益成熟。但由于DEM數據精度的差異、處理方法不同和人為因素影響等,流域水文特征提取的精度會受到很大影響,如何不斷進行技術創新、提高精度是日后研究的重點。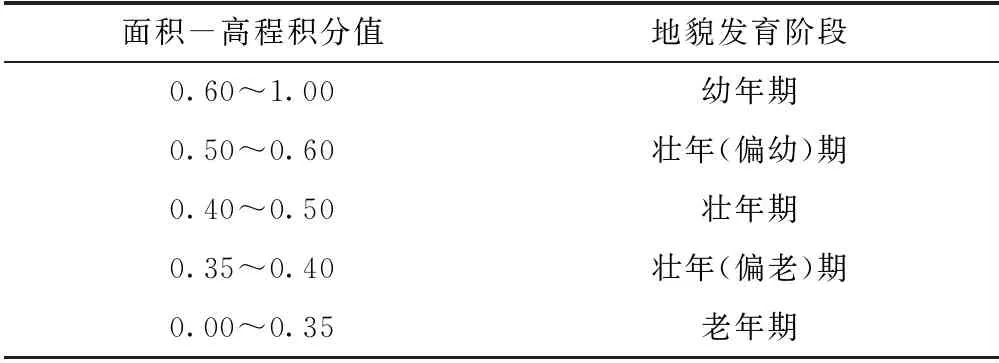
5 結論與討論

