基于EMD-EEMD-LSTM的大壩變形預測模型

董 泳，劉肖峰，李云波，賈玉豪

(1.南京市水利規劃設計院股份有限公司，江蘇 南京 210022；2.河海大學水利水電學院，江蘇 南京 210024；3.上海勘測設計研究院有限公司，上海 200335)

0 引 言

大壩作為一種重要的基礎設施，在社會、經濟發展過程中發揮著重要作用，一旦發生事故，將對下游人民的生命財產造成巨大損失[1]。因此，對大壩行為趨勢的分析和預估是至關重要的。變形作為大壩結構性態最直觀的指標，選取高效的分析模型對其進行建模、分析，是大壩安全評價系統的重要課題之一[2]。

傳統的大壩變形分析方法主要分為3大類——確定性模型、統計模型以及混合模型。這3種模型的缺點主要是建模難、精度不能滿足要求等。為此一些學者將機器學習(ML)相關算法引入大壩變形分析領域，如人工神經網絡、支持向量機、極限學習機等方法[3-5]。以往ML方法主要針對影響大壩變形的環境因素(如水壓、溫度和時效等)進行多變量建模，從而構建變形預測模型。然而實際工程中，大壩變形監測數據的波動性往往較強，模型的輸入變量不能很好地捕捉變形的變化趨勢，造成了模型預測精度不足。如何降低原始變形數據的波動性，是從本質上提高變形預測精度的關鍵。因此本文引入了Huang等[6]提出的經驗模態分解(EMD)，旨在將原始變形序列分為若干穩定的分量，進而深入挖掘大壩變形的內在規律。與VMD、小波變換等傳統信號分解方法相比，EMD具有不受分解層數以及小波基選擇影響的優勢，已經在大壩安全監控系統的構建中得到了廣泛的應用[7-9]。然而，由于大壩變形的復雜非線性，經過EMD分解得到的高頻分量依舊給模型的預測帶來一定難度。

為了解決高頻分量非線性強、預測精度低等問題，本文提出基于EEMD[10]對其進行再次分解，從而降低高頻分量的非線性，最大程度上降低高頻分量對整體變形預測精度的影響。經過2次分解得到的一系列變形分量代表變形不同尺度下的變化規律。對于某個分量，其可能受某一環境影響因子的影響或多因素耦合影響。為了解決模型輸入變量難以確定的問題，本文提出了使用LSTM[11]對各分量進行建模，考慮各個時間序列的時序相關性。通過查閱文獻可知，LSTM的預測性能優于傳統ML方法。LSTM獨特的“門”結構能夠針對時間序列的非線性進行建模分析，通過滑窗的滑動實現預測結果的輸出。對各分量分別構建LSTM模型，將得到的預測結果進行疊加，得到最終的變形預測結果。

1 研究方法

1.1 EMD

經驗模態分解(EMD)是一種對非線性非平穩信號進行平滑處理的方法。通過EMD分解可以將復雜的原始信號分解為一系列光滑的分量d。為了使得到的時間序列的分解結果有意義，d有2個約束條件：①數據序列的極值點個數與過零點個數之差≤1；②上、下包絡線在任意時刻的均值為0。EMD的主要表達式為

(1)

式中，di(t)和r(t)分別為第i個分量以及殘差序列；x(t)表示為原始序列，本文中表示大壩原始變形序列。

1.2 EEMD

變形時間序列經EMD分解，將得到一組具有不同頻率的分量。其中變形信息的不確定性主要包含在高頻分量中，且變形規律難以捕捉，這將造成高頻分量的預測結果誤差較大。本文針對高頻分量提出了二次分解法，旨在分離出高頻分量中的有效變形信息，削弱波動性對預測模型輸出結果的負面影響，以提高變形預測精度。考慮到高頻分量的復雜非線性，為了更有效提取高頻分量中的變形信息，本文提出使用EEMD算法對其進行再次分解。

EEMD方法將白噪聲加入原始信號[12]，然后使用EMD方法對這些新獲得的序列進行處理，解決了EMD存在的模態混淆缺陷。EEMD原理為

(1)步驟1。將白噪聲加入原始序列x(t)，生成新的時間序列y(t)。

(2)步驟2。利用EMD方法對新生成的時間序列進行分解，得到新的di(t)和r(t)；。

(2)

(3)

1.3 LSTM

LSTM神經網絡是一種特殊的遞歸神經網絡，具有學習長期依賴關系的能力。與簡單的RNN不同，LSTM神經網絡有內置的機制(輸入門it、遺忘門ft和輸出門ot)來控制信息在整個過程中是如何被記憶或者丟棄的，克服了RNN固有的梯度消失問題。LSTM神經網絡的體系結構如圖1所示，并由下列公式進行定義。

(4)

(5)

(6)

(7)

ht=ottanh(ct)

(8)

(9)

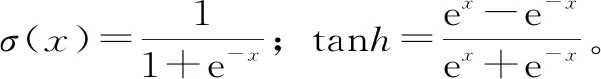
2 模型構建

本文通過EMD分解原始變形序列得到一組包含不同頻率的分量(d1，d2，…，dN，r)；對于其中的高頻分量di，通過EEMD算法進行分解得到一組趨于穩定的分量(D1，D2，…，DP，R)；所有分量集合包含了原始變形序列的全部變形信息，選取LSTM作為各分量的時序預測模型，建模并預測得到各分量的預測結果后，將所有預測結果疊加得到最終的輸出，從而構建了基于EMD-EEMD-LSTM的大壩變形預測模型，具體流程如圖2所示。

3 實例驗證

3.1 工程簡介和數據采集

以某碾壓混凝土拱壩為例，具體說明EMD-EEMD-LSTM模型在大壩變形預測中的優越性。拱壩壩軸線與河道斜交，左右兩岸地形不對稱。建基面高程130.0 m，壩頂高程234.6 m，最大壩高104.6 m。壩體共分為12個壩段，大壩變形由布置于壩中的垂線系統監測得到。本文選取第4壩段ZC2測點2015年1月1日～2017年8月31日期間的徑向變形數據作為分析對象，變形觀測數據每日讀取一次。在數據分析之前，對其中包含的異常值和缺失值進行預處理。將缺失值進行剔除，并采用線性差值法處理異常值，最終可得966個變形讀數，變形曲線見圖3。同時將時段劃分為訓練組、驗證組和預測組，其中2015年1月1日～2017年7月2日時段內的數據為訓練組，2017年7月3日～2017年8月1日時段內的數據為驗證組，2017年8月2日～2017年8月31日時段內的數據為預測組。訓練組用以訓練LSTM模型，驗證組用以檢驗訓練模型的有效性，預測組用以預測評估未來時段內的大壩變形發展趨勢。

3.2 EMD、EEMD分解結果

利用EMD算法對原始變形序列進行分解，分解結果見圖4。由圖4可知，EMD能夠將原始序列分解為不同頻率的變形信號組合。其中d3、d4為中頻信號，d5、d6以及r為低頻信號，上述信號通過LSTM建模預測，將得到預期的預測結果。而d1、d2兩個高頻變形信號表現出明顯的波動性，這將給變形預測帶來一定的難度，為此本文對信號d1+d2進行再次分解，以深入挖掘高頻信號中蘊含的變形信息，基于EEMD的高頻分解結果見圖5。

由圖5可知，經過EEMD分解，高頻分量可以被分為11個分量。通過中低頻分量可以看出，第1次分解得到的高頻分量中依舊包含有用的變形信息，雖然該部分變形信息占比較低，然而忽略此部分將使得預測結果缺乏可靠性，且對預測結果的精度造成一定的負面影響。針對EEMD分解得到的11個變量，由于此部分變形幅度不大，因此采用組合建模方法，即將它們分為高、中、低頻3組進行組合預測。其中，D1、D2為高頻組合，D3、D4、D5為中頻組合，剩余分量為低頻組合。

3.3 變形預測結果及對比分析

針對分量d3～d6、r以及二次分解后的3種頻率組合分別建立LSTM模型，為對比基于EEMD的高頻分解的有效性，考察EEMD分解前后預測結果的精度差異，同時選取了單一多變量BP模型以及LSTM模型作為對比模型，各個模型的預測結果見圖6。

由圖6可知，各模型預測結果變化曲線差異較大。其中，BP模型對應的變化曲線與實測值的誤差最大，說明單一的多變量模型并不能很好地捕捉變形的非線性；LSTM模型的預測結果更接近真實值，然而仍舊無法精確捕捉變形的波動性。相比之下，通過信號分解技術分解后的變形預測結果明顯優于單一模型。

圖7為各模型預測結果殘差圖。由圖7可知，BP模型的預測殘差變化幅度明顯高于其中模型，LSTM次之；而EMD-LSTM和EMD-EEMD-LSTM模型對應的殘差與x軸形成的誤差面積明顯小于單一模型。為了進一步對比高頻分量分解前后預測結果的精確度，說明挖掘高頻分量的必要性，選取RMSE、MAE以及預測結果箱線圖作為模型預測性能評價指標，對不同模型的預測結果進行量化評價，各模型的評價指標如圖8所示。

由圖8可知，分析各模型的預測性能，其中BP和LSTM模型的評價指標明顯低于經過2個結合信號分解的模型。對于EMD-LSTM和EMD-EEMD-LSTM模型，可知后者的RMSE和MAE取值均低于前者，驗證了討論高頻分量中有效變形信息的重要性。由箱線圖(圖8a)可以看出，EMD-EEMD-LSTM對應的箱線圖與實測值代表的箱線圖各項指標最為接近，說明對于大壩這種重要的基礎設施來說，變形高頻分量中的變形信息不可忽視。

4 結 論

本文構建了一種基于EMD-EEMD-LSTM模型的大壩變形預測分析方法，該方法具有較高的大壩變形預測精度。其中，EMD模型能夠有效降低原始序列的波動性；基于EEMD對高頻分量進行再次分解，能夠進一步降低非線性對變形預測結果的負面影響，深入挖掘變形高頻分量中蘊含的變形信息，提升預測性能；選取LSTM作為各分量變形預測器，對每個分量進行建模，考慮變形時序依賴性，提高了模型的預測精度。