基于數據驅動的高校學生心理健康評估研究

李剛，陳潔

(1.陜西中醫藥大學第二附屬醫院，陜西，咸陽 712000;2.西安市大數據服務中心，陜西，西安 710001)

0 引言

大學生對自己未來的人生飽含期待，充滿著激情和活力，但他們抗壓能力嚴重不足，易受外界干擾，心理變化較大，導致許多大學生不自覺地產生不同的心理健康問題[1-3]。

針對大學生日趨嚴重的心理健康問題，該課題越來越多成為學術研究主題[4-5]。有學者在基于積極心理學視角下研究的學生心理健康評估方法，采用Cronbach’s α系數和Pearson相關系數評價量表的內容效度獲取學生心理健康評估結果[6]；有學者基于多特征融合的在線論壇研究的用戶心理健康自動評估方法，基于多特征設計的融合心理健康評估框架與貪婪法、降噪自編碼器等策略相結合的方式，實現對學生的心理健康評估目的[7]。雖然這兩種方法都能有效評估學生的心理健康狀態，但是不完全體現出在校大學生的心理健康，基于此，本文進行了基于數據驅動的大學生心理健康評估研究，數據驅動是一種解決問題的方法，當我們不能簡單且準確的解決一個問題的時候，就可以根據實際的歷史數據和關系數據構造與真實情況相近的模型對問題進行求解，在適應過程中具有實踐指導作用。

1 數據驅動的大學生心理健康評估方法

1.1 基于數據驅動的改進模糊聚類算法

1.1.1 改進模糊聚類算法模型

假設數據集為n，類別數為c，類別數取值區間為[1,n]。

定義1hik為可能隸屬度，表示第k個對象與第i類別之間相對應的隸屬程度，取值區間為[1,n]，該類別的隸屬度與代表該類別的點和聚類中心之間的距離相關，間距越小，則隸屬度越大，無關其他聚類中心。

定義2sik為不確定性隸屬度，表示第k個對象屬于第i類別的可能性，取值為0和1，不確定性隸屬度具備記憶存儲功能，能夠記憶以往的迭代過程。

(1)

本算法被定義為不確定性隸屬關系的前提條件時不同聚類的隸屬度均為1時，這與其他概念中的不確定性有所不同[8]。

定義3 算法的準則函數基于參數hik、sik進行構造，即：

(2)

結合定義3和拉格朗日求值方法計算hik，拉格朗日函數為

(3)

F對hik求偏導，即：

(4)

(5)

F對λ求偏導，即：

(6)

在式(6)中代入hik，得：

(7)

在式(5)中代入式(7)，即：

(8)

求解最終可能隸屬度公式為

(9)

所有數據點基于參數tik、sik進行加權求均值，求解新的聚類中心公式為

(10)

1.1.2 評價指標體系構建

依據改進模糊聚類算法聚類結果，構建心理健康評估指標體系如圖1所示。通過學習、生活、未來發展3個方面的共計11項指標衡量大學生心理健康[13]。

圖1 大學生心理健康評估指標體系

1.2 大學生心理健康模糊綜合評估設計過程

(1) 針對評估對象確定指標論域A,

A={a1,a2,…,an}

(11)

其中，n表示評估指標數，大學生心理健康的評估體系采用兩層結構式，評估對象為大學生心理健康狀況，指標論域表示一級指標。

(2) 確定評估等級論域B,

B={b1,b2,…,bm}

(12)

其中，m表示評估等級數，各等級與各模糊子集呈一一對應的關系，一般m為奇數，可方便利用其中間等級進行評估。評估標準B分別為優秀、良好、一般、較差、差。

(3) 建立模糊關系矩陣C。針對待評估項目依次對所有評估指標進行量化，模糊關系矩陣C根據模糊子集各等級的隸屬度C(ai)確定

(13)

式中，C為從A到B的模糊關系，cij表示第i個因素獲取的第j種評估結果。

(4) 確定評估因素的模糊權向量D,

D={d1,d2,…,dn}

(14)

對于評估對象來說，所有的評估指標不具備相同重要性，每個因素對總體影響性不同。在模糊評估中，di表示ai對模糊自己的隸屬度，采用歸一化方法確定模糊權重，然后進行合成。

(5) 模糊評估結果向量E通過合成算子對D和C合成得到C中不同的行反映的是不同的指標對模糊子集的隸屬程度，對不同的行采用D進行綜合即得到所有等級模糊子集的隸屬程度，模糊綜合評估的模型為

=(e1,e2,…,en)

(15)

式中，C表示模糊變換器，用于指標論域A和評估等級論域B之間，每個模糊向量都能得到相應的綜合評估結果E，評估過程如圖2所示。

圖2 模糊評估過程示意圖

(6) 分析模糊評估結果向量。每個大學生的心理健康評估結果為一個模糊評估值集合，與其他評估方法相比其結果中包含了更豐富的信息量，對心理健康指數的評估結果通過評估等級呈現在相對應的數值集合上。模糊綜合評估模型的工作流程如圖3所示。

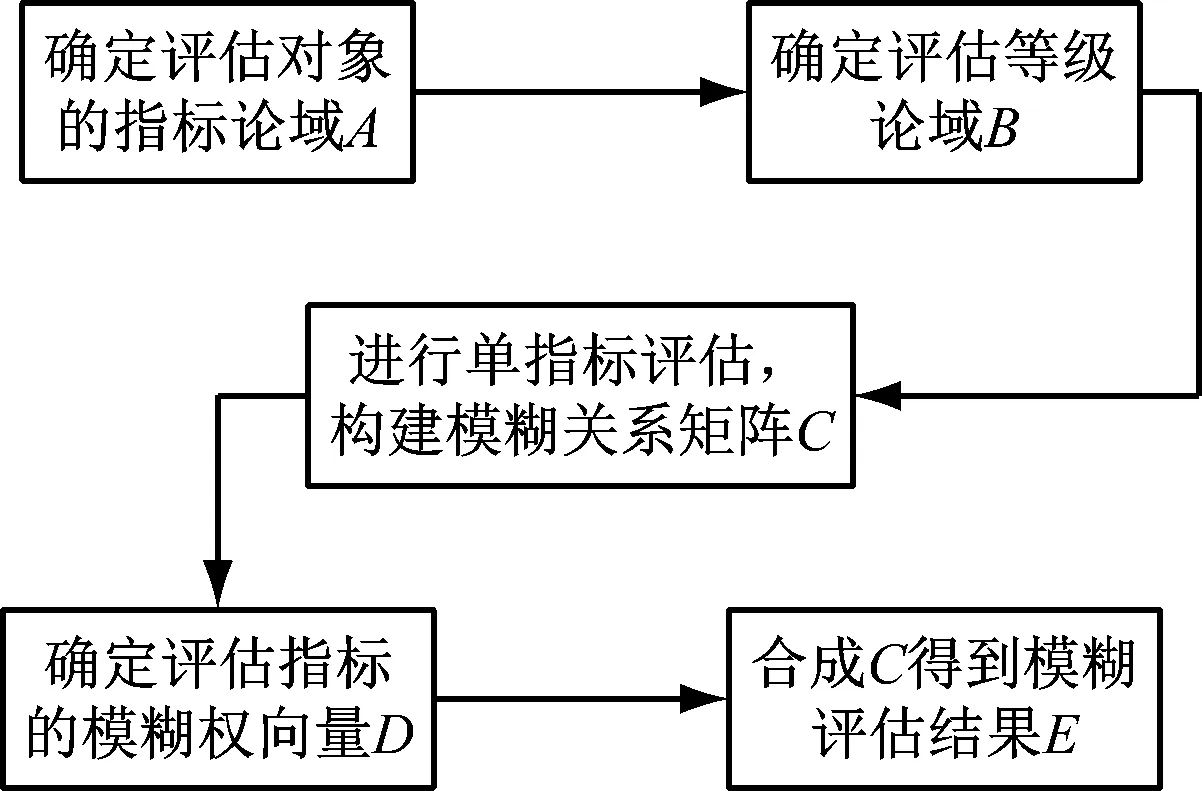
圖3 大學生心理健康模糊評估模型的工作流程

2 實驗結果與分析

選取某高校為實驗對象，對該校近3年的3 600名應屆畢業生進行心理普查、學生基本情況、社會支持度等歷史數據作為實驗數據集。利用本文評估方法對大學生心理健康進行評估，評估指標見圖1。邀請10位心理健康方面權威專家對每個治療進行打分，每位專家的平均值為二級指標評估結果。估計等級結合被評估學生心理健康狀況，評估標準如表1所示。為了驗證本文評估方法的有效性，分別采用文獻[8]和文獻[9]方法進行對比實驗。

表1 大學生心理健康評估標準

從3 600名大學生的歷史數據中選取1 000個數據樣本并將其分為5組數據集，采用3種方法分別進行數聚類性能測試，對比結果如圖4所示。由圖4聚類結果可知，隨著數據樣本個數的增多，3種方法所耗時間均呈上升趨勢，但是本文方法的聚類效果與文獻[8]方法和文獻[9]方法具有明顯的優勢，耗時短，運動平穩，時間控制在0.1 s以內，這是因為本文方法在聚類方面獨具記憶存儲功能，能夠有效減少循環次數，確保結果的穩定性。

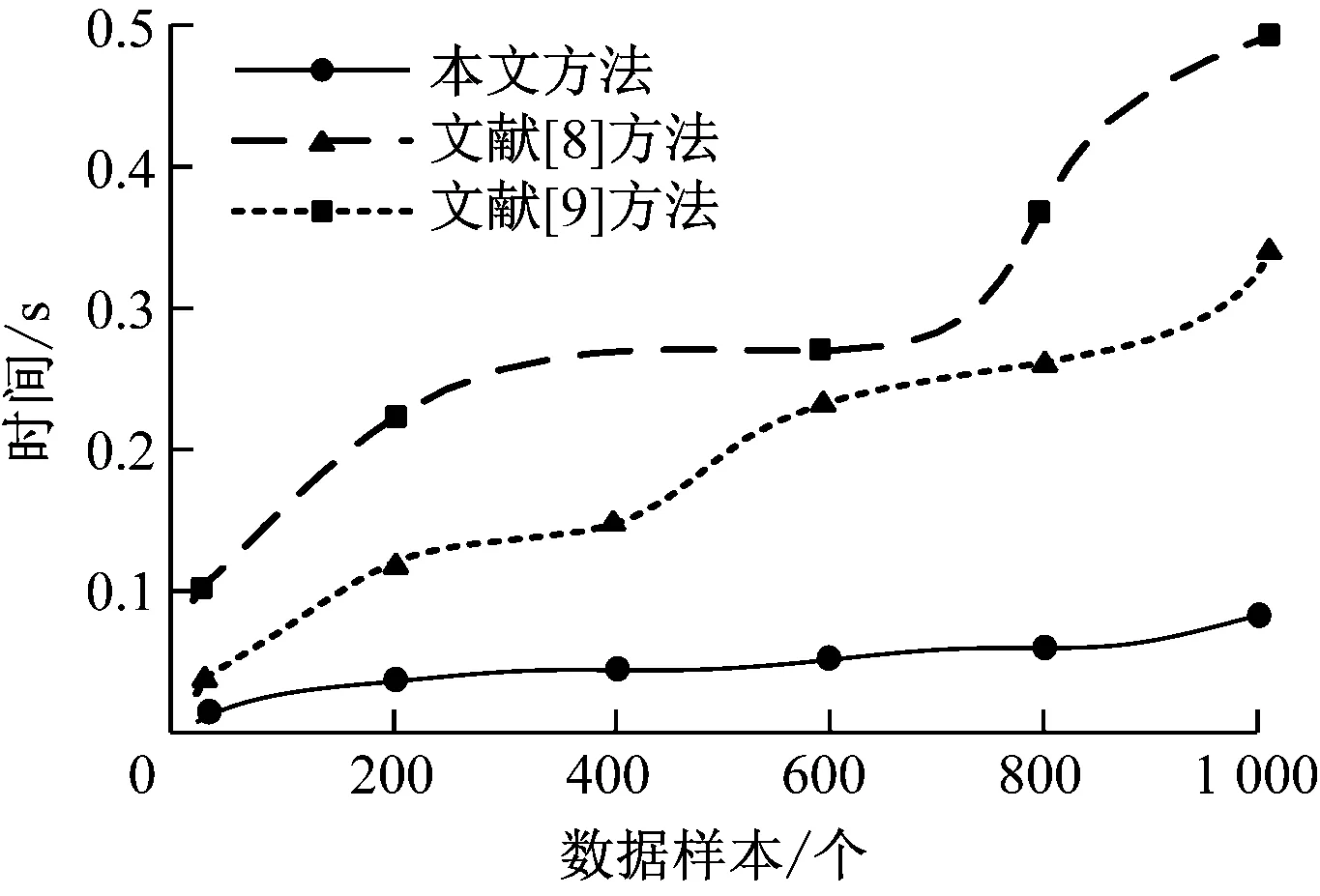
圖4 數據聚類對比結果示意圖

本文方法獲取各指標模糊權重明細如表2所示。

表2 大學生心理健康指標權重明細表

根據以上指標權重，計算獲取大學生心理健康各指標評分及相對應綜合評估等級，評估結果如表3所示。

表3 大學生心理健康指標綜合評估結果

參考專家實際綜合評估結果，將表3的本文評估結果與文獻[8]和文獻[9]的評估結果進行對比，對比結果如表4所示。由表4可知，采用本文方法進行的大學生心理健康評估結果與實際評估結果一致，效果與兩種對比評估方法具有明顯準確率的優勢，說明本文基于數據驅動的大學生心理健康評估方法切實有效，能夠為大學生心理健康的評估提供有力的參考價值。

表4 大學生心理健康評估對比結果表

綜合運用3種誤差評價指標，分別為平方均根差(RMSE)、歸一化方均根差(NRMSE)以及平均絕對百分比誤差(MAPE)，確保評估效果檢驗的全面性與客觀性。

(16)

(17)

(18)

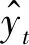
3種方法評估誤差比對結果如圖5所示。由圖5可知，3種方法的誤差結果中，本文方法的誤差值始終保持最低，RMSE、NRMSE和MAPE誤差值分別為0.276、0.382和0.468，表明本文方法的預測誤差最低，能夠滿足對大學生心理健康評估的需求。

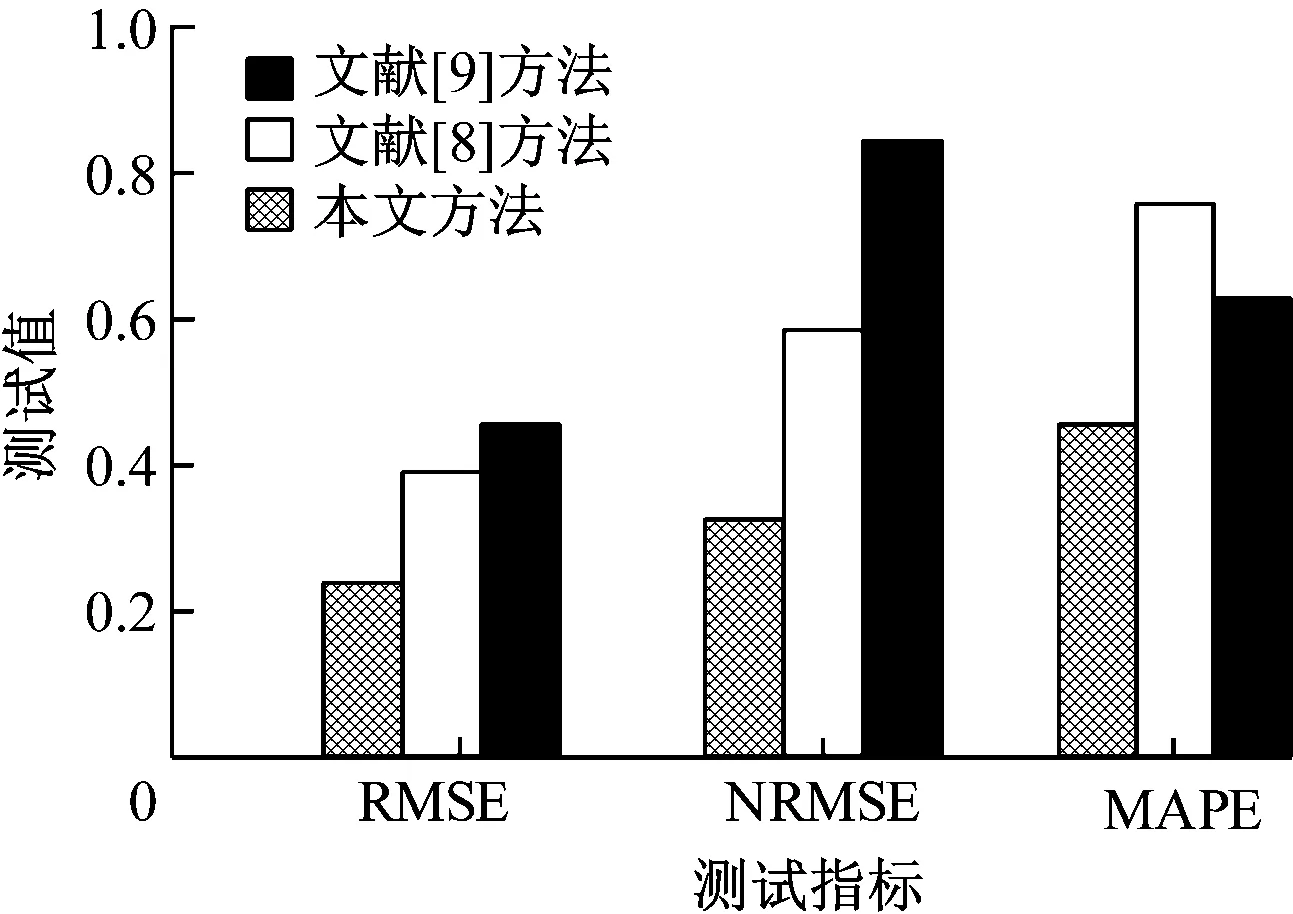
圖5 誤差測試結果

3 總結

大學生在面對學業、家庭和即將踏入社會的三重壓力之下，出現心理健康問題的逐年增多，通過對在校大學生近幾年的心理普查、學生基本情況、社會支持度等調查的歷史數據，提出基于數據驅動的大學生心理健康評估方法，該方法通過改進模糊聚類算法和模糊綜合評估模型的高效結合，有效降低數據冗長的影響，減少計算循環次數，確保結果的穩定性，提升大學身心理健康評估指標的合理性和正確性，促使結果量化，方便對評估結果進行分析和比較，有效消減評估過程中人為因素的干擾，具有良好的客觀性和科學性。試驗結果表明，該方法能有切實有效地評估大學生心理健康狀況。在后續的研究中，可以針對調查問卷的編制進行合理性的加強，盡量保證所有問題都具有適用價值且符合實際情況，完善問題的選項全面問題。