離散小波變換快速探測衛星機動算法

李 亮，劉亞勇，李 慧,2，王仁龍，李夢浩

(1.哈爾濱工程大學 智能科學與工程學院，哈爾濱 150001；2.哈爾濱工程大學青島船舶科技有限公司，山東 青島 266000)

衛星在圍繞地球運動過程中除受地球引力影響，還受其他攝動力影響，導致其偏離預定軌道。為使衛星在預定軌道上運行，通常采用機動的方式調整衛星軌道。而全球導航定位用戶在進行精密定位時依賴高精度、高可靠的軌道產品，當衛星發生機動時，需要對機動衛星單獨處理以生成高精度軌道信息，即使使用廣播星歷定位，也必須對衛星機動進行監測，否則存在定位風險。除此之外，當衛星軌道發生機動時，該衛星服務中斷，降低了衛星的連續性和可用性，從而影響衛星導航系統的定位、導航和授時服務性能[1]。為盡可能減少衛星機動不可用時間以及實現準確切換定軌策略目的[2]，需要對衛星的機動周期進行實時監測。歐洲定軌中心(The center for orbit determination in Europe，CODE)發布GPS衛星機動信息，但至少延時1 d，無法滿足實時應用需求，而美國海岸警衛導航中心(U.S.coast guard navigation center，NAVCEN)發布的GPS衛星機動信息，普通用戶無獲取權限。廣播星歷的健康標志位同樣會給出衛星預警信息，但此預警信息并不僅僅針對衛星機動，且廣播星歷的健康標志會提前標志機動開始時間，滯后標志機動結束時間，極大減少了衛星可用時間。除此之外，廣播星歷還有可能出現錯誤或丟失情況[3]。

為能準確地給出衛星機動信息，許多學者[4-6]開展了相關研究。由于利用衛星星歷信息和觀測量信息進行衛星機動探測及周期確定不需要額外測量設備，故被廣泛應用。部分學者[7]僅利用廣播星歷進行衛星機動探測，基于廣播星歷的軌道互差探測BDS軌道機動，但該方法主要應用于事后處理。基于廣播星歷的衛星機動探測方法受廣播星歷更新頻率限制，導致衛星機動探測準確度不高。Huang等[8]提出了一種結合廣播星歷和偽距的衛星機動探測方法，該方法能顯著提高探測實時性。為進一步提高衛星機動探測及周期確定的準確度，有學者提出利用更高測量精度的載波相位進行衛星機動探測。Qiao等[9]提出了利用載波相位三差殘差探測BDS衛星機動周期，該方法能準確探測衛星機動周期，其通過線性回歸確定衛星周期，但其機動探測結果可能受基線選取的影響[10]。除此之外，還有學者利用軌道監測數據探測衛星機動，杜蘭等[11]利用中國區域定位系統(China area positioning system，CAPS)的軌道監測數據確定GEO衛星的軌道機動，但普通用戶沒有獲取該數據的權限。

小波變換是數字信號處理領域中一種對信號進行時頻分析和處理的重要方法，可有效在時域、頻域對信號進行局部化分析。本文基于載波相位三差模型進行衛星機動探測及周期確定，考慮差分測量噪聲的影響，提出利用離散小波變換進行衛星機動分析，基于多分辨分析對載波相位三差殘差進行分解，通過分析不同頻率特性的近似系數和細節系數，提取衛星機動特性，綜合載波相位三差及小波變換的優勢，實現衛星機動快速探測及周期確定。

1 離散小波變換的衛星機動探測

1.1 載波相位三差模型

在t時刻載波相位觀測量方程:

λφ(t)=r(t)+T(t)+c(dtu(t)-dts(t))-

I(t)-λN+δ(t)

(1)

式中：r(t)為衛星與接收機間的距離，T(t)、I(t)分別為對流層和電離層延遲誤差，dtu(t)、dts(t)分別為接收機鐘差及衛星鐘差，N為整周模糊度，λ為對應的波長，δ(t)為測量噪聲，c為光速。

在周跳探測策略上，采用電離層殘差法和M-W組合聯合探測；在誤差處理策略上，采用無電離層組合消除電離層延遲；Saastamoinen模型及Niell投影函數補償對流層延遲；采用星間和站間差分分別消除與接收機及衛星有關的誤差；為進一步消除整周模糊度，將觀測方程進行歷元間差分：

(2)

基于載波相位三差觀測方程，提取載波相位三差殘差量：

(3)

式中η(tk)為與衛星機動相關的變量。

在衛星未發生機動的情況下，η(tk)為0，由式(3)得到的載波相位三差殘差相對較小；衛星機動發生后，η(tk)不再為0，廣播星歷不能很好地預測衛星實際軌道，載波相位三差殘差會逐漸增大，機動結束后，衛星軌道又趨于平穩。利用載波相位三差殘差在衛星機動發生及結束時刻的變化特性，實現衛星機動探測并確定機動周期。需要注意的是，雖然式(2)中的載波相位三差消除了大部分觀測誤差，但無電離層組合以及三次差分的操作都會增加測量噪聲，如果此時不考慮測量噪聲的影響，將導致不能快速準確地探測衛星機動周期，故在利用載波相位三差殘差模型時必須考慮測量噪聲的影響。

1.2 基于離散小波變換的衛星機動信息確定

傳統基于載波相位三差模型的衛星機動探測方法采用多歷元線性回歸減弱測量噪聲，但多歷元累積的方法增加了機動探測反應時間，且該方法的機動探測結果可能受基線選取的影響。考慮到機動信號和載波相位三差殘差噪聲進行小波變換后在各尺度上所表現的特性不同，本文利用小波變換對載波相位三差殘差去噪，消除噪聲對機動信號的影響，以此探測其在機動開始時刻和結束時刻的局部變化特性，實現衛星機動快速探測及周期確定。

根據式(3)，載波相位三差殘差包含與衛星機動相關的變量和噪聲兩部分，可將其簡寫為δ(t)=η(t)+ε(t)，其中η(t)為與衛星機動相關的變量，ε(t)為載波相位三差殘差噪聲，且近似服從零均值正態分布[12]。不妨設噪聲ε(t)均值為0、方差為σ2，用ψ(t)、Wε(m,n)分別表示選取的小波函數以及ε(t)的小波變換，則載波相位三差殘差噪聲小波變換后的平均功率Wε(m,n)為

E{|Wε(m,n)|2}=

?E{ε(u)ε(v)}ψm(n-u)ψm(n-v)dudv=

σ2‖ψ‖2/m

(4)

式中：‖·‖2為平方積分，m為尺度因子，n為平移因子，u、v為積分變量。從式(4)可得載波相位三差殘差噪聲ε(t)小波變換后的平均功率與尺度因子m成反比，這與機動變量η(t)小波變換后各尺度上表現的特性不同[13]，小波變換正是通過多分辨分析，最終實現去噪目的。

小波變換的多分辨分析建立在空間概念上，在不同的尺度下，構造尺度函數向量空間V和小波函數向量空間W，載波相位三差殘差δ(t)在尺度空間V做卷積得到表示低頻信息的近似系數，在小波空間W做卷積得到表示高頻信息的細節系數。考慮到機動期間db1小波函數與載波相位三差殘差的階躍特性相似性較高[14]，選取db1小波函數作為小波基，對載波相位三差殘差δ(t)進行分解:

(5)

式中：j為分解層數，最大分解層數N滿足2N≤Length(δ)，其中Length(δ)表示載波相位三差殘差δ(t)長度，φm,n(t)=2-m/2φ(2-mt-n)為尺度函數，ψm,n(t)=2-m/2ψ(2-mt-n)為小波函數。cj,n為載波相位三差殘差δ投影到尺度空間Vm形成的近似系數；dm,n為載波相位三差殘差δ(t)投影到小波空間Wm形成的細節系數。

理論上，分解層數越高去噪效果越好，但分解層數過高可能會丟失載波相位三差殘差的機動信息[15]，考慮到第1層受噪聲影響較為嚴重[16]，所以分解層數一般大于1。由近似系數分解成下一層分解層數的近似系數和細節系數[17]，如果近似系數和細節系數探測結果相同，表明此時由近似系數分解的細節系數已體現機動信息，繼續分解有可能丟失機動信息，故本文以基于近似系數與細節系數的衛星機動探測結果為依據，機動開始時刻相同的最低分解層數作為衛星機動探測分解層數。小波變換將大部分能量集中在少數、幅值比較大的小波系數上，而載波相位三差殘差的噪聲分布在各個尺度上，其小波系數幅值較小，考慮到噪聲近似服從零均值高斯分布[12]，利用Donoho[18]提出的閾值公式作為閾值, 即

(6)

式中：n為三差殘差長度;λ為噪聲標準方差，其估計公式[19]：λ=median|ri|/0.674 5,其中γi為小波分解第1層分解所對應的小波系數，median為求中值。考慮細節系數隨分解層數的增加而衰減，故對細節系數的噪聲標準方差λ做進一步處理[16]：λ′=λ/In(J+1)，其中，J為當前分解層數。

離散小波變換能有效消除噪聲對三差殘差的影響，放大衛星機動起止時刻三差殘差的變化幅值，根據衛星機動未發生時的三差殘差數據確定的判斷閾值，可有效實現衛星機動探測。基于離散小波變換進行衛星機動探測及周期確定時，綜合利用載波相位三差和小波變換優勢，實現快速準確的衛星機動信息探測。

2 結果分析

為了驗證本文所提方法性能，本文設計了兩個實驗，利用不同基線長度測站的觀測數據，分別針對GPS和BDS衛星進行衛星機動探測及周期確定，并與載波相位三差的線性回歸方法進行比較。對于GPS衛星，利用IGS的METG、REDU、TLSE、WTZ3、WTZZ及DYNG共6個測站，其中DYNG作為主測站，與其他測站構成5條基線。對于BDS衛星，利用IGS的GMSD、JFNG、MIZU、PTGG及ANMG共5個測站，其中ANMG作為主測站，與其他測站構成4條基線。實驗所選擇的觀測數據見表1，數據采樣率為30 s。

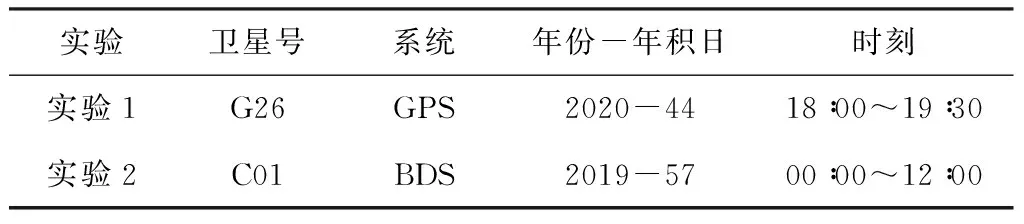
表1 實驗所選取的衛星觀測數據

對于實驗1，根據CODE所公布的衛星機動信息，選取真實發生的G26機動衛星，取其機動時觀測數據，構建載波相位三差探測模型，利用離散小波變換進行衛星機動探測及周期確定。圖1、2分別給出了基于線性回歸和利用本文所提方法的機動探測及周期確定結果。圖1中，圖1(a)～(d)分別給出了5條基線所對應的載波相位三差殘差曲線、以及利用2～4個歷元做線性回歸的機動探測曲線。紅色實線為機動探測周期結果，紅色虛線為判斷閾值[1,7,20]。圖2中，圖2(a)、(c)、(e)分別給出了分解層數為3層的近似系數d3、d2及d1曲線；圖2(b)、(d)、(f)分別給出了分解層數為3層的細節系數a3、a2及a1曲線。紅色實線為探測機動周期結果，紅色虛線為判斷閾值，其判斷閾值按式(6)進行確定。

表2給出了CODE所公布的GPS衛星G26的衛星機動信息、傳統基于線性回歸方法的機動探測結果，以及利用本文所提方法的機動探測結果，其中，線性回歸方法的探測結果選取的是反應最敏感的TLSE-DYNG基線結果。考慮到GPS衛星機動時間一般不超過2 min[21]，本文在利用線性回歸方法時最多選取了4個歷元。

以表2中CODE公布的機動開始時間為真值，從結果上看，采用離散小波變換探測機動開始時間滯后真值1 s；采用2～4個歷元做線性回歸探測機動開始時間分別滯后真值1 s、提前真值29 s和提前真值59 s。雖然CODE沒有公布衛星機動的結束時間，但由圖1(b)可知，利用2個歷元做線性回歸探測的機動周期為一個點，與機動周期為一段時間的常識有矛盾之處，故基于線性回歸存在提前確定衛星機動結束時間的可能。對于線性回歸方法而言，線性回歸選取歷元較少時，斜率易受噪聲影響導致誤判風險；線性回歸選取歷元較多時，能有效降低因噪聲導致的誤判，但所需探測反應時間也會相應增加，如圖1及表2結果所示，故基于線性回歸的方法需在可靠性和時效性之間做一定權衡。離散小波變換能有效消除測量噪聲對載波相位三差殘差影響，放大載波相位三差殘差的局部特性，實現平滑載波相位三差殘差目的，且其單歷元處理方式不需要額外增加探測反應時間。綜上所述可得，相比于線性回歸方法，基于離散小波變換方法探測衛星機動更快速、準確。

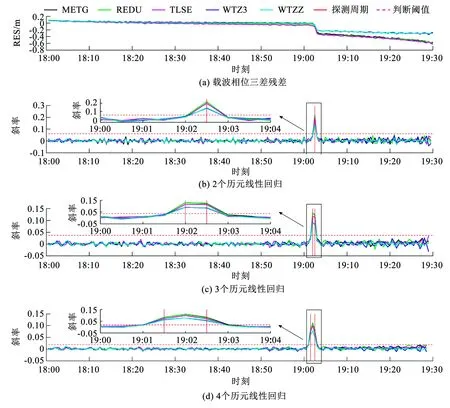
圖1 基于線性回歸方法探測GPS衛星機動及周期確定

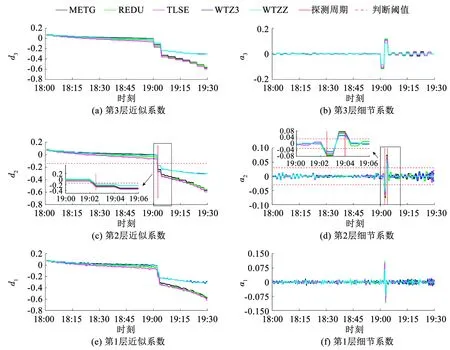
圖2 基于離散小波變換探測GPS衛星機動及周期確定

表2 GPS機動探測及周期確定結果

對于實驗2，綜合精密星歷缺失性、廣播星歷健康標志和軌控指令信息，選取真實發生的C01衛星，取其機動時觀測數據，建立載波相位三差探測模型，利用離散小波變換進行機動探測及周期確定。圖3、4分別給出了基于線性回歸和利用本文所提方法的機動探測及周期確定結果。圖3(a)～(d)分別給出了載波相位三差殘差曲線、以及以利用10、20和30個歷元做線性回歸的機動探測曲線，紅色實線為探測機動周期結果，紅色虛線為判斷閾值。圖4(a)、(c)、(e)、(g)、(i)分別給出了分解層數為5層的近似系數d5、d4、d3、d2、d1曲線；圖4(b)、(d)、(f)、(h)、(j)分別給出了分解層數為5層的細節系數a5、a4、a3、a2、a1曲線。紅色實線為探測機動周期結果，紅色虛線為判斷閾值。

表3給出了關于C01衛星的軌控指令、傳統基于線性回歸方法的探測結果，以及利用本文所提方法的探測結果。其中，基于線性回歸方法探測機動及周期的結果選取的是反應最敏感的ANMG-GMSD基線結果。

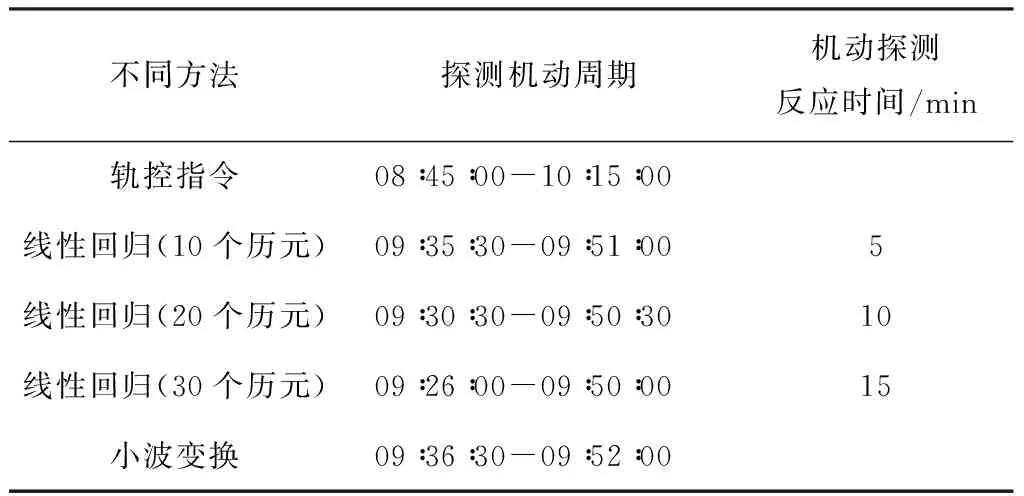
表3 BDS機動探測及周期確定結果

由表3結果可知，利用小波變換和線性回歸方法得到的BDS衛星機動周期都在軌控指令的機動時間段內。由于未查到BDS衛星公布的機動信息，所以無法給出探測結果的準確度，但就結果而言，BDS探測結果與GPS探測結果保持一致。通過對圖3對比，利用線性回歸探測衛星機動時其機動探測結果可能受基線選取的影響。圖4表明，利用小波變換探測衛星機動時其不同基線探測到的衛星機動發生時刻及周期結果一致。綜上所述，相比于傳統的線性回歸方法，離散小波變換在進行衛星機動快速探測及周期確定時具有一定優勢。

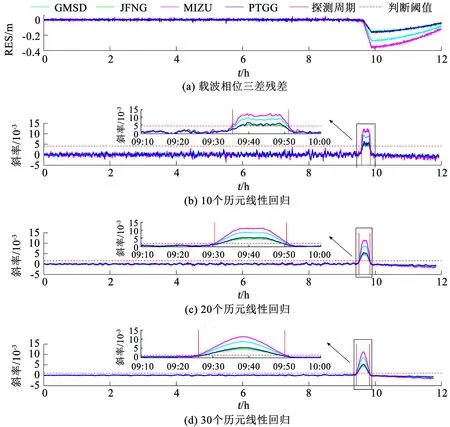
圖3 基于線性回歸方法探測BDS衛星機動及周期確定

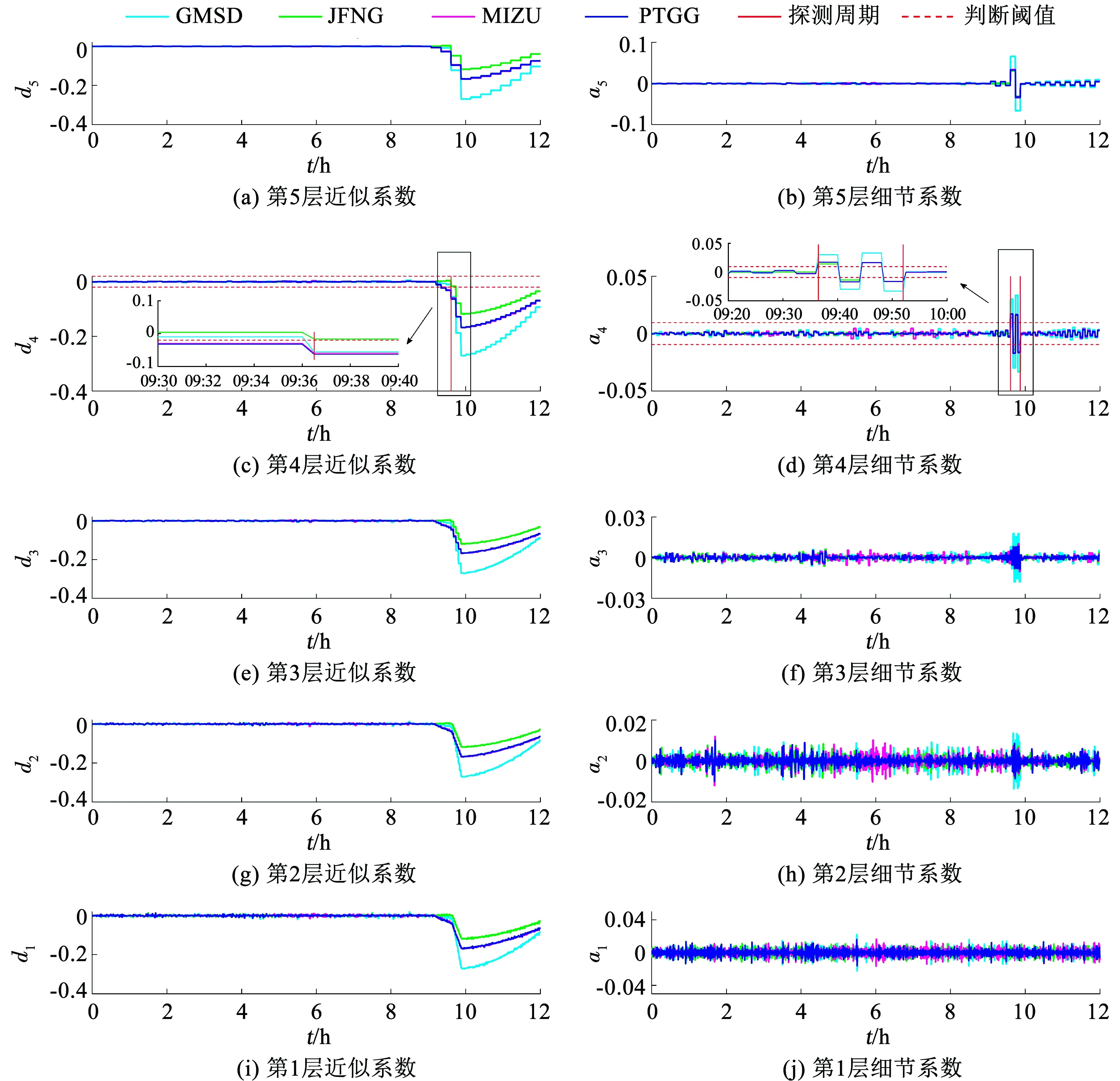
圖4 基于小波變換探測BDS衛星機動及周期確定

3 結 論

1)相比于傳統基于線性回歸的方法，基于離散小波變換探測GPS衛星機動開始時刻偏離真值1 s，優于傳統方法。

2)不同基線探測到的衛星機動發生時刻及周期結果一致，單歷元處理方式不需要額外增加探測反應時間，能更及時準確的探測衛星機動并確定其周期。