不確定離散時間系統的狀態逼近事件觸發控制

丁三波,劉亞拴

(河北工業大學 人工智能與數據科學學院，天津 300401)

近年來,隨著網絡技術的迅速發展,網絡化控制系統由于成本較低,便于維護,可以有效地實現遠程控制和遠程診斷,受到了學者的廣泛關注。周期采樣是一種常見的網絡化控制方法[1-2]。此方法根據給定的采樣周期,對系統輸出進行周期性采樣和傳輸。周期采樣利于系統的設計與分析,但可能會產生冗余采樣信號,造成通信帶寬的浪費。為避免此類問題,學者引入了事件觸發控制(Event-triggered control,ETC)。在事件觸發控制中,只有在某一變量超過給定閾值時,控制器執行更新任務,有效地節約了通信帶寬資源[3-5]。目前,事件觸發控制已經廣泛存在于各個領域的研究[6-8]。

離散時間系統是很常見的物理系統,針對離散時間系統的事件觸發控制也屢見不鮮。如Shen等[9]研究了一類具有隨機參數和不完全測量的離散時間混合時滯神經網絡的事件觸發狀態估計問題。Hu等[10]研究了一類離散時間隨機系統的事件觸發機制控制問題,探討了數據丟包問題。文獻[9-10]設計的事件觸發方案均采用了傳統的誤差測量方式,以狀態反饋為例,傳統測量誤差的定義為常采樣信號與系統當前狀態之間的差。在觸發時刻kl到下一次觸發時刻kl+1內,被控對象在控制信號的作用下,系統狀態的演化整體趨勢是收斂的,所以測量誤差會隨時間逐步增大,而這會導致測量誤差很容易超過預設的常數閾值或時變閾值,使得相鄰觸發間隔較小,造成較高的觸發頻率。

本文從狀態預測或逼近的角度,針對離散線性/非線性系統分別逐段構造了狀態逼近解,逼近解可以跟隨閉環系統離散狀態的局部變化趨勢,實現減少測量誤差的目的。設計了基于狀態逼近解的事件觸發控制器,并得到了閉環系統的穩定性判據。同時,本文將該方法結合動態事件觸發策略[11],通過增大觸發閾值,達到更好的控制效果。最后通過數值仿真驗證了該方法的有效性,并與傳統事件觸發控制器[15-16]作比較,表明狀態逼近法可以有效地降低采樣次數,減少通訊帶寬的浪費。

1 線性系統的事件觸發控制

考慮如下離散線性系統:

x(k+1)=(A+ΔA)x(k)+Bu(k)

(1)

式中：x(k)=col[x1(k),x2(k),…,xn(k)]∈Rn為狀態變量,u(k)∈Rq為要設計的控制器,A∈Rn×n和B∈Rn×q為常數矩陣。ΔA∈Rn×n為參數擾動。假設ΔA=EΣ(k)F,其中ΣT(k)Σ(k)≤I,E∈Rn×p,F∈Rp×n為已知矩陣。

在傳統的事件觸發控制[15-16]中,往往將控制器u(k)設計為

u(k)=Kx(kl)

(2)

式中kl≤k≤kl+1-1,K∈Rq×n為控制增益矩陣。通過定義ef(k)=x(k)-x(kl),設計如下觸發條件：

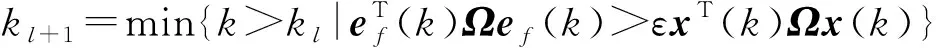
(3)

式中：Ω∈Rn×n為一個正定的常數矩陣,ε>0為觸發閾值。

事件觸發策略(3)實際上是將常采樣信號x(kl)代替了控制器u(k)=Kx(k)中的系統狀態x(k),或者說是常采樣信號x(kl)用來逼近系統當前狀態x(k),這容易造成較高的觸發頻率。基于上述方法的局限性,本文提出基于狀態逼近的事件觸發控制方法。

對于無參數擾動系統：

x(k+1)=Ax(k)+Bu(k)

(4)

式中控制器為u(k)=Kx(k),系統(4)在k∈[kl,kl+1-1]上的解析解為x(k)=(A+BK)k-klx(kl),不妨將該解析解視為系統(1)的狀態的逼近解來研究系統(1)的穩定性。

令xg(k)=(A+BK)k-klx(kl),構造控制器為

u(k)=Kxg(k)

(5)

式中k∈[kl,kl+1-1]。定義測量誤差eg(k)=x(k)-xg(k),設計事件觸發條件為：

k0=0

(6)

式中：Ω∈Rn×n為正定常數矩陣,ε>0為觸發閾值。

聯立系統(1)和控制器(5),可以得出：

Δx(k)=(A+ΔA+BK-I)x(k)-BKeg(k)

(7)

式中Δx(k)=x(k+1)-x(k)。

在定理1中,給出了系統(1)基于控制器(5)和事件觸發條件(6)的控制下漸近穩定的充分條件。

定理1對于給定的觸發閾值ε>0和控制增益矩陣K∈Rm×n。如果存在恰當維數的矩陣P>0,Ω>0,N=col[N1,N2,N3],以及正常數r0使下列條件成立,則事件觸發條件(6)和控制器(5)可以保證閉環系統(1)是漸近穩定的。

(8)

其中：

r0FTF+εΩ

證明考慮下面Lyapunov函數：

V(k)=xT(k)Px(k)

(9)

計算V(k)的差分,可得

ΔV(k)=V(k+1)-V(k)=

xT(k+1)Px(k+1)-xT(k)Px(k)=

ΔxT(k)Px(k)+2xT(k)Px(k)

(10)

令ξg(k)=col{x(k),Δx(k),eg(k)},則對于適當維數的矩陣N=col[N1,N2,N3],以及正常數r0,下列不等式條件成立：

EΣ(k)F)x(k)-BKeg(k)]≤

BKeg(k)]+r0xT(k)FTFx(k)+

(11)

對于k∈[kl,kl+1-1],由事件觸發條件(6),有

(12)

聯立式(10)～(12)可得

(13)

其中

(14)

根據Schur補定理,條件(8)等價于Π<0。證明完成。

文獻[12]提出了離散時間系統的動態事件觸發方案。這種方法實際上是增大了觸發的閾值。本文的方法完全可以結合動態事件觸發方案進行推廣,進而降低網絡的通訊負擔。定義如下γ(k)變量:

εxT(k)Ωx(k)

(15)

式中γ(0)≥0,相應的動態觸發條件為：

k0=0

εxT(k)Ωx(k))<0}

(16)

式中0<ρ<1,θ≥1/ρ。文獻[12]證明了在區間k∈[0,+∞)中,γ(k)≥0,所以動態觸發條件(16)可能會比靜態觸發條件(6)產生較少的觸發次數。

注2觸發條件(16)在增加了觸發閾值的同時,減小了測量誤差的取值。從降低系統通訊負擔的角度而言,將是一種更好的選擇。當θ趨于無窮時,觸發條件(6)可以看作式(16)的極限情況。

推論1對于給定的觸發閾值ε>0和控制增益矩陣K∈m×n。如果定理1中的條件成立,則在事件觸發條件(16)和控制器(5)可以保證閉環系統(1)是漸近穩定的。

ΔxT(k)PΔx(k)+2ΔxT(k)Px(k)+

εxT(k)Ωx(k)≤

ΔxT(k)PΔx(k)+2ΔxT(k)Px(k)-

(17)

將式(17)代替定理1中的式(10)和式(12),其余證明與定理1相似,在這里不再贅述。

2 非線性系統的事件觸發控制

考慮如下離散非線性系統：

x(k+1)=(A+ΔA)x(k)+

(W+ΔW)f(W0x(k))+Bu(k)

(18)

式中x(k)=col[x1(k),x2(k),…,xn(k)]∈n為狀態變量,u(k)=Kx(k)為要設計的控制器,W∈Rn×m和W0∈Rm×n為系統矩陣。ΔA∈Rn×n,ΔW∈Rn×m為參數擾動。且滿足ΔA=EΣ(k)F,ΔW=GΘ(k)H,其中ΣT(k)Σ(k)≤I,ΘT(k)Θ(k)≤I。E、G、F、H為已知矩陣。非線性函數f(·)=col[f1(·),f2(·),…,fm(·)]。其余符號與系統(1)一致。

假設函數fr(·)滿足fr(0)=0以及下面條件：

(19)

式中l1r、l2r為已知常數。記l1=diag{l11,l12,…,l1m},l2=diag{l21,l22,…,l2m}。

注3本文假設非線性系統(18)滿足Lipschitz條件(19)。在實際中,有許多系統滿足該條件[17-20],例如經典的Hopfield神經網絡模型、Lur’e型系統、蔡氏電路系統以及Ikeda-type振蕩器等。

對任意滿足條件l1≤L≤l2的常對角矩陣L,將離散非線性系統(18)線性化近似為帶有參數擾動的線性系統:

x(k+1)=[A+ΔA+(W+ΔW)LW0]x(k)+Bu(k)

(20)

對于無擾動離散系統：

x(k+1)=(A+WLW0)x(k)+Bu(k)

(21)

式中控制器為u(k)=Kx(k)。可以得到系統(21)在k∈[kl,kl+1-1]的解析解為

xh(k)=(A+BK+WLW0)k-klx(kl)

(22)

將解析解(22)當作系統(18)的逼近解。構造如下控制器：

u(k)=Kxh(k)

(23)

式中k∈[kl,kl+1-1]。定義eh(k)=x(k)-xh(k)。設計如下事件觸發條件：

k0=0

(24)

式中：Ω∈Rn×n為正定常數矩陣,ε>0為觸發閾值。

聯立系統(18)和控制器(23),可得

Δx(k)=(A+ΔA+BK-I)x(k)+

(W+ΔW)f(W0x(k))-BKeh(k)

(25)

式中Δx(k)=x(k+1)-x(k)。

定理2給出了離散非線性系統(18)基于控制器(23)與事件觸發條件(24)的穩定性判據。

定理2對于給定的觸發閾值ε>0和控制增益矩陣K∈Rm×n。如果存在恰當維數的矩陣P>0,Ω>0,N=col[N1,N2,N3,N4],m階對角正定矩陣Λ,以及正常數r1,r2,使下列條件成立,則事件觸發條件(24)和控制器(23)可以保證閉環系統(17)是漸近穩定的。

(26)

其中：

證明考慮下面Lyapunov函數：

V(k)=xT(k)Px(k)

(27)

計算V(k)的差分,可得

ΔV(k)=V(k+1)-V(k)=

xT(k+1)Px(k+1)-xT(k)Px(k)=

ΔxT(k)PΔx(k)+2xT(k)Px(k)

(28)

令ξh(k)=col{x(k),Δx(k),f(W0x(k)),eg(k)},則對于適當維數的矩陣N=col[N1,N2,N3,N4],以及正常數r1,r2下列不等式條件成立：

EΣ(k)F)×x(k)+(W+GΘ(k)H)f(W0x(k))-

(A+BK-I)x(k)+Wf(W0x(k))-BKeh(k)]+

r1xT(k)FTFx(k)+r2fT(W0x(k))HTHf(W0x(k))

(29)

考慮關于非線性函數f(·),根據式(19),對于任何正定矩陣Λ∈m×m,下列不等式成立:

0≤2(f(W0x(k))-l2W0x(k))TΛ×
(l1W0x(k)-f(W0x(k)))

(30)

對于k∈[kl,kl+1-1],根據事件觸發條件(24),有

(31)

聯立式(28)～(31)可得

(32)

式中

(33)

根據Schur補定理,條件(26)等價于Ξ<0。證明完成。

定理2的結果可以結合動態事件觸發策略進一步提高。定義如下μ(k)變量：

εxT(k)Ωx(k)

(34)

式中μ(0)≥0,由文獻[12]可知,在區間k∈[0,+∞)中,μ(k)≥0。相應動態觸發條件為：

k0=0

εxT(k)Ωx(k))<0}

(35)

式中0<ρ<1,θ≥1/ρ。

推論2對于給定的觸發閾值ε>0,θ>0和控制增益矩陣K∈Rm×n。如果定理2中的條件成立,則事件觸發條件(35)和控制器(23)可以保證系統(18)是漸近穩定的。

注4通過構造逼近解,本文將測量誤差e(k)=x(k)-x(kl)改為eg(k)和eh(k),減小了測量誤差的取值,有利于降低事件觸發的次數。但是與傳統事件觸發方法相比[15-16],本文所提方法并不會降低穩定性判據的保守性。

3 數值仿真

例1在本例中,考慮倒立擺模型,其線性化動力學模型如下:

(36)

式中θ為擺角,u(t)為作用在小車上的力,擺錘質量m=0.1 kg,小車質量M=0.1 kg,擺錘長度l=0.136 m,這里取重力加速度g=9.8 m/s2,用ΔA=EΣ(t)F用以描述倒立擺控制系統的參數不確定性[21],取E=col[0.4 0.8],F=[0 0.1],Σ(t)=sin(t)。

令采樣周期為0.005 s,通過將上式離散化得到:

(37)

考慮具有以下參數的離散線性系統,取K=[2.854 8 0.475 8],觸發閾值ε=0.1。

通過LMI工具箱解線性矩陣不等式(8),可得

(38)

選取初始條件為x(0)=col[0.2,0],迭代次數取T=500。

圖1、2分別為本文所提出的方法與傳統事件觸發方法[15-16]的控制器響應。本文所提出的方法觸發次數為5次,傳統事件觸發方法的觸發次數為69次。很容易看出本文所提出的方法策略能有效減少觸發次數。

圖1 控制器響應：狀態逼近ETC方法

圖2 控制器響應：傳統ETC[15-16]

接下來,比較本文中基于狀態逼近的動態觸發控制與文獻[12]的仿真結果,令式(15)中的ρ=0.5,θ=3,迭代次數為T=500。圖3、4為控制器響

圖3 控制器響應和動態變量γ(k)：狀態逼近動態ETC

圖4 控制器響應和動態變量γ(k)：文獻[12]的動態ETC

應和動態變量γ(k)的仿真結果。仿真中,本文中基于動態觸發條件(6)產生的事件觸發次數為4次,而文獻[12]中的方法為28次,是本文方法的7倍。因此,本文提出的狀態逼近法可以有效減少事件發生的次數。

通過LMI工具箱解出線性矩陣不等式(26),可得

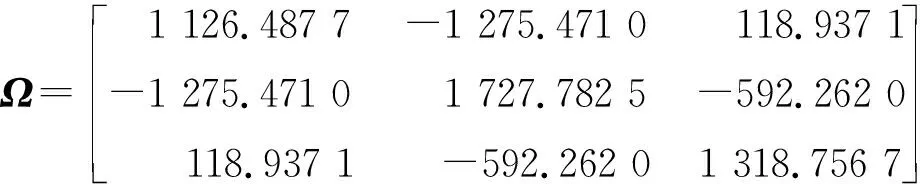
(39)

選擇初始條件x(0)=col[3,-3,4],迭代次數T=50。圖5、6分別給出了本文所提出方法與傳統事件觸發方法[15-16]對應的事件觸發間隔。本文所提出的方法與傳統事件觸發方法的采樣數量分別為6、22,可以看出本文所提出的方法策略能有效減少采樣數量。

圖5 事件觸發時刻和間隔：狀態逼近ETC方法

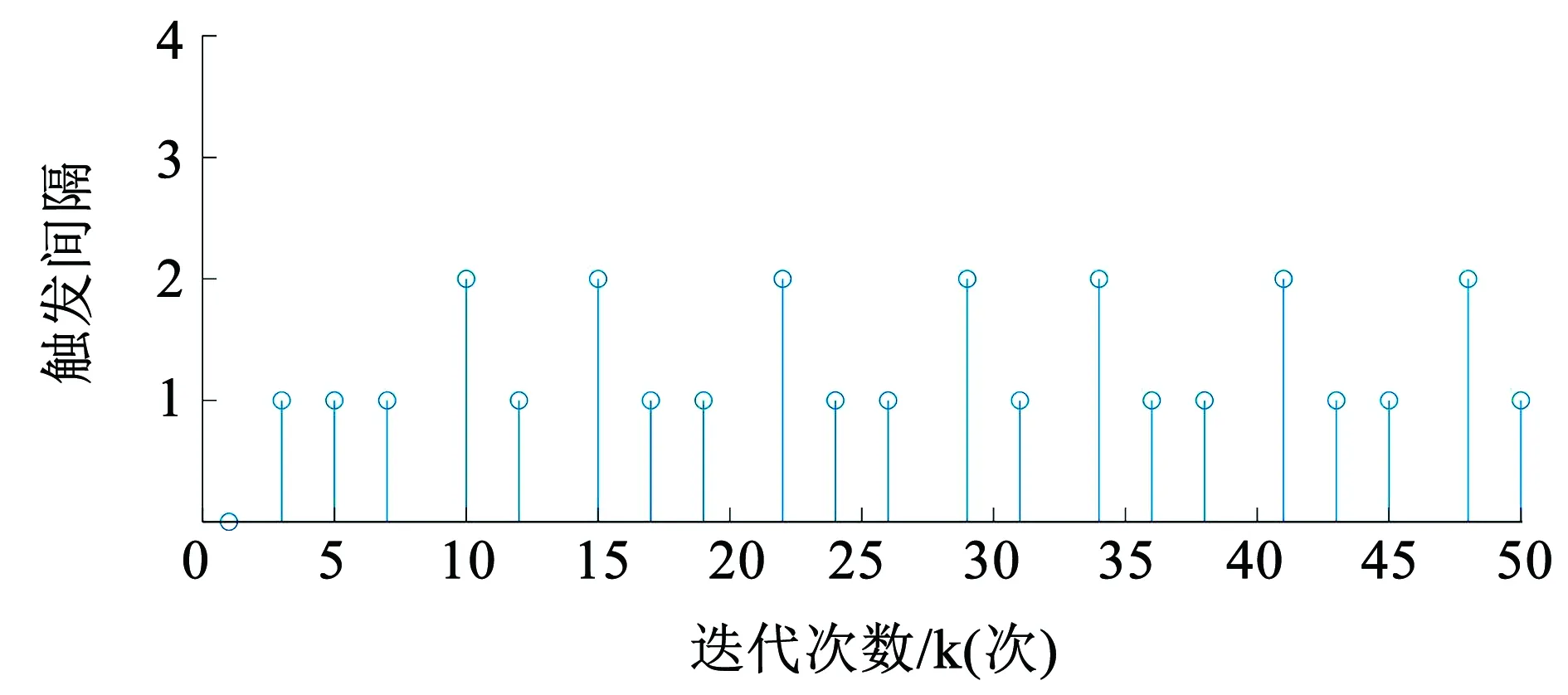
圖6 事件觸發時刻和間隔：傳統ETC[15-16]

將文獻[12]所用方法與本文中基于狀態逼近的動態觸發作比較,設動態觸發條件(34)中的ρ=0.5,θ=3,迭代次數為T=50。圖7、8分別給出了動態變量μ(k)和事件觸發間隔的仿真結果。在圖7中,本文方法基于動態觸發條件(35)產生的事件數為4次,而在圖8中,文獻[12]中的方法為14次。本文提出的狀態逼近法可以有效減少事件發生的次數,并且本文方法結合動態事件觸發策略進一步減少了事件觸發次數。

圖7 動態變量μ(k)與事件觸發時刻和間隔：狀態逼近動態ETC

圖8 動態變量μ(k)與事件觸發時刻和間隔：文獻[12]的動態ETC

4 結 論

1)針對帶有參數擾動的線性/非線性系統,利用系統矩陣、采樣信號和無擾動離散線性系統解析解的定義逐段構造狀態逼近解,逼近解可以一定程度上跟隨系統當前狀態,減少測量誤差。設計了基于狀態逼近解的控制器和事件觸發條件。通過構造Lyapunov泛函分別給出了線性/非線性系統穩定的充分條件。并將狀態逼近法結合動態事件觸發策略做了進一步研究。

2)通過列舉倒立擺系統和蔡氏電路的實驗表明,相比傳統事件觸發控制方法,本文提出基于狀態逼近的事件觸發控制方法產生的事件次數更少,可以有效地節約通訊帶寬資源。