一種針對聚類問題的量子主成分分析算法

劉文杰 王博思 陳君琇

1(數(shù)字取證教育部工程研究中心(南京信息工程大學) 南京 210044)2(南京信息工程大學計算機與軟件學院 南京 210044)(wenjie@163.com)

聚類是將一組物理抽象對象分類為由相似對象組成的不同類別的過程.聚類產(chǎn)生的集群是一組數(shù)據(jù)對象，同一集群中的對象相似程度高.因此，聚類研究的是樣本在尺度空間上的分布.在聚類問題[1-2]上，聚類樣本數(shù)據(jù)中的離群點容易影響簇中心的選擇，進而影響聚類結(jié)果，且樣本點規(guī)模的擴大會造成算法需要在樣本點間的距離計算上消耗大量計算資源，這些都導致算法在復雜度和精度上存在一些不足.為了研究量子計算在聚類問題上的應用與擴展，Horn等人[3]提出量子聚類(quantum clustering, QC)算法.不同于經(jīng)典的K-Means[4]和K-Medians[5]算法，QC算法在迭代過程中用于聚類的度量距離相對固定，學習速率不容易確定.2007年，李志華等人[6-8]對QC算法進行了改進，提出了基于距離的量子聚類算法，該算法解決了QC算法在迭代過程中的缺陷.此外，Zhang等人[9]通過指數(shù)距離函數(shù)對QC算法中樣本點間距離計算方法和迭代過程作出改進，提出了新型量子聚類算法,EDQC算法.但上述算法的簇中心的選取很容易受到離群點以及聚類規(guī)模的影響，當待聚類的樣本點線性不可分時，這些算法聚類效果并不是很好.

針對聚類問題，本文提出了一種新型的量子主成分分析算法——QPCA算法(quantum principal component analysis algorithm)，結(jié)合奇異值分解[10]的思想，用于提取待聚類數(shù)據(jù)的主成分，以便選取更為準確的簇中心.此外，本文采用了Liu等人[11]提出的量子最小值搜索算法，通過優(yōu)化不同樣本點之間距離最小值搜索過程，降低聚類的迭代次數(shù).實驗部分采用Cirq[12]量子編程框架進行量子仿真驗證，由于可使用的量子比特位數(shù)的限制，本文完成了小規(guī)模數(shù)據(jù)集情況下的量子實驗的驗證.

本文工作的主要貢獻有3個方面:

1) 提出采用新型量子主成分分析算法，選取更為準確的簇中心，減少異常值對簇中心選擇的影響;

2) 利用指數(shù)距離公式計算樣本點到簇中心的距離，同時采用量子最小值搜索算法加快最短距離搜索，減少聚類所需迭代次數(shù)；

3) 采用Cirq量子編程框架完成相關(guān)量子仿真實驗，比已有的傳統(tǒng)及量子聚類算法、QC-PCA算法在聚類準確度和性能上都有不同程度的改進.

1 相關(guān)工作

本節(jié)中主要介紹主成分分析算法以及量子主成分分析算法的基本定義以及作用特點.

主成分分析(principal component analysis, PCA)算法[13-14]常用于數(shù)據(jù)分析，能夠在保持數(shù)據(jù)集主要信息的同時降低數(shù)據(jù)集的維數(shù)(特征的數(shù)量).

量子主成分分析(QPCA)[15-18]是一種將量子計算與傳統(tǒng)機器學習結(jié)合的量子降維算法，能夠獲取數(shù)據(jù)矩陣中最具有代表性的特征值對應的特征向量并進行重構(gòu). 具體的算法過程為：

假設存在具有n個樣本點且每個樣本點具有m維特征的數(shù)據(jù)集用矩陣X=(xn)來表示，每個樣本點可以被表示為xi=(xij)，1≤i≤n，1≤j≤m，σ代表奇異值.

初始態(tài)制備階段應用2個酉操作：

UM:|i〉|0〉

(1)

UN:|0〉|j〉

(2)

其中

酉操作UM和UN分別用于編碼并得到初始樣本點的量子態(tài)形式以及在幅度上編碼樣本點范數(shù).X*為X的伴隨矩陣.利用式(1)、式(2)這2個酉操作能夠幫助操縱量子比特，得到需要的初始態(tài)：

|ψs〉=UMUN|0〉|0〉=

(3)

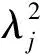
(4)

σj表示奇異值.而量子態(tài)能夠被表示為

(5)

其中|uj〉和|vj〉分別保存著矩陣的左奇異向量和右奇異向量.通過額外增加輔助量子位，求解密度矩陣的冪，并且對幺正運算W執(zhí)行相位估計：

W=(2MM?-IND)(2NN?-IND)=

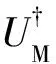
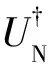
(6)

得到

(7)

(8)

執(zhí)行逆相位估計，將特征值寄存器釋放，執(zhí)行受控旋轉(zhuǎn)操作CR(β1),CR(β2),…,CR(βd)，得到:

CR(βj):|j〉|0〉

(9)

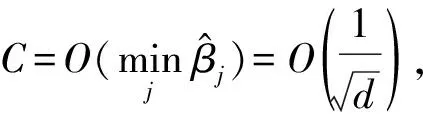
(10)

經(jīng)過投影測量最終可以得到:

(11)

經(jīng)過上述步驟，存儲所有數(shù)據(jù)點信息的量子態(tài)|ψs〉被轉(zhuǎn)換成低維的量子態(tài)|ψe〉：

|ψs〉|ψe〉

(12)

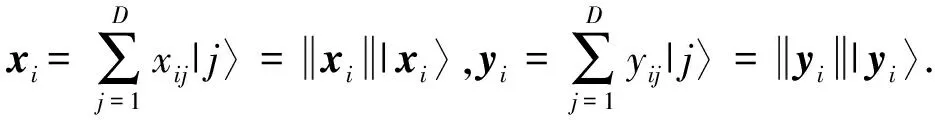
2 針對聚類問題的量子主成分分析算法

針對聚類問題，本文提出了QC-PCA算法.先將待聚類的原始數(shù)據(jù)集矩陣進行奇異值分解，利用預設的閾值更新奇異值并得到主成分，對原始數(shù)據(jù)集特征進行篩選和提取，再利用薛定諤方程表示篩選后的數(shù)據(jù)特征，分別采用波函數(shù)和勢函數(shù)描述數(shù)據(jù)分布狀態(tài)和勢能大小，從而減少異常值對簇中心選取的影響，選取具有代表性的簇中心.此外，采用量子最小值搜索算法[11]尋找距離樣本點最近的簇中心，減少聚類所需迭代次數(shù).重復上述步驟，遍歷所有樣本點并完成聚類.本文提出的算法過程可以用算法1來描述.

算法1.QC-PCA算法.

輸入：N個數(shù)據(jù)、維度M、k個聚類、閾值τ；

輸出：樣本聚類結(jié)果.

① 準備量子態(tài)：|ψ1〉=|0〉|0〉L|0〉C|ψs〉B；

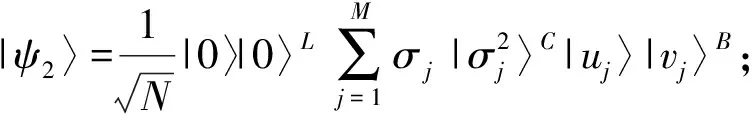
④ 選取k個簇中心ci，i∈[1,k]；

⑤ fori=1,2,…,N-kdo

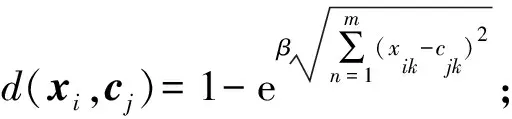
⑦ 搜索樣本點到簇中心的最小距離，聚類；

⑧ end for

⑨ 計算各類的質(zhì)心作為新的簇中心；

⑩ 重復迭代⑤～⑨直至前后簇中心相同，完成聚類.

假設存在具有n個樣本點且每個樣本點具有m維特征的數(shù)據(jù)集用矩陣X=(xn)來表示，每個樣本點可以被表示為xi=(xij)，1≤i≤n，1≤j≤m，σ代表奇異值，δ，k，τ分別表示測量距離，聚類類別以及預設的閾值.QC-PCA算法能夠通過6個步驟來進行描述：

步驟1.量子態(tài)準備.

利用UM,UN這2個酉操作分別編碼并得到初始樣本點的量子態(tài)形式以及在幅度上編碼樣本點范數(shù)，產(chǎn)生想要的初態(tài).制備處于|0〉量子態(tài)的量子比特，通過式(3)得到最終的量子態(tài)為|ψ1〉=|0〉|0〉L|0〉C|ψs〉B.

步驟2.奇異值分解.

步驟1得到的初態(tài)能夠采用主成分分析的思想進行奇異值分解，得到前d個表示數(shù)據(jù)主要特征的量子態(tài)形式的主成分|v1〉,|v2〉,…,|vd〉，它們相應的所占方差比例可以用式(4)表示.根據(jù)式(1)(2)(4)，式(3)可以被化簡為

(13)

通過額外增加輔助量子位，求解密度矩陣的冪，并且在第2個寄存器上利用式(6)對幺正運算W執(zhí)行相位估計，得到量子態(tài)：

(14)

步驟3.更新奇異值提取主成分.

(15)

(16)

利用2種受控旋轉(zhuǎn)操作消除了閾值變化，實現(xiàn)了高保真、高概率的矩陣逼近.量子主成分分析算法的整個電路設計如圖1所示：

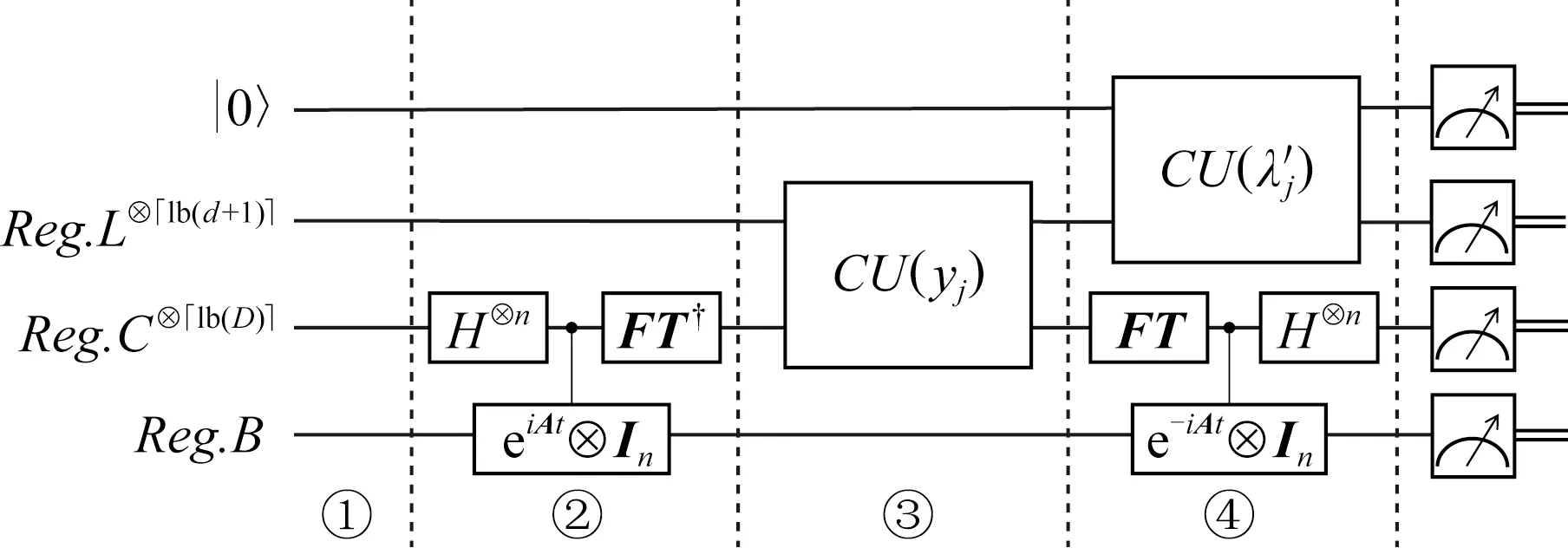
Fig. 1 Circuit of quantum principal components analysis algorithm圖1 量子主成分分析算法電路

步驟4.選取簇中心.

篩選后的數(shù)據(jù)集樣本點可以被描述為量子力學中的希爾伯特空間中的粒子，其分布能夠用薛定諤方程表示為

(17)

其中H,V,E分別表示哈密頓算符，勢函數(shù)以及H可能的特征值.利用勢函數(shù)V可以寫出特征態(tài)函數(shù)，也就是高斯波函數(shù)表示：

(18)

除此之外，在給定波函數(shù)Ψ時，利用Schr?dinger方程也可以求解出決定樣本點分布的勢函數(shù)V，即

i∈{1,2,…,k}.

(19)

簇中心ci可以用從勢能值集合中挑選出的k個最小值數(shù)據(jù)xi來表示.

步驟5.計算樣本點到各簇中心距離.

隨機挑選出一個樣本點數(shù)據(jù)，利用指數(shù)距離公式

(20)

(21)

步驟6.聚類.

計算樣本點到各個簇中心點的距離，并采用量子最小值搜索算法[11]找到最小距離，完成該樣本點的聚類.重復步驟5的過程，直到所有的數(shù)據(jù)樣本被聚類為k個類別.然后計算同類別數(shù)據(jù)點的質(zhì)心作為新的簇中心，假設第i個聚類中有f(X,Y)個點，則新的簇中心為

重復步驟5以及步驟6直至前后2個簇中心相同，聚類結(jié)束.

3 實驗仿真

3.1 實驗設計

為了驗證本算法的有效性和可行性，本文采用Cirq[12]量子編程框架實現(xiàn)小規(guī)模數(shù)據(jù)集下的量子算法驗證.所有實驗均運行在一臺配置顯存為40 GB的NVIDIA Tesla A100顯卡，Intel GOLD 5220R CPU，256 GB內(nèi)存的服務器上，編譯語言采用Python，編譯器采用Pycharm.

Table 1 Dimensional Features of Some Data Points to be Clustered

Fig. 2 Distribution of data points to be clustered圖2 待聚類數(shù)據(jù)點分布

S0～S119為隨機生成的120個樣本點，F(xiàn)0～F5表示每個樣本點具有6個特征.待聚類數(shù)據(jù)點分布示意圖如圖2所示，相同顏色深度的點代表生成的相同類別的數(shù)據(jù).

3.2 實驗流程及對比分析

首先根據(jù)數(shù)據(jù)集，利用UM和UN酉操作準備量子態(tài):

|ψ1〉=|0〉|0〉L|0〉C|ψs〉B,

(22)

其中|ψs〉滿足式(3).接著將|ψ1〉進行奇異值分解，并附加量子位，執(zhí)行酉操作W的相位估計，得到量子態(tài)：

(23)

計算yj=(σj-τ)/σj=1-τ/σj，yj∈[0,1)，執(zhí)行受控旋轉(zhuǎn)，根據(jù)旋轉(zhuǎn)角度，利用受控旋轉(zhuǎn)門將奇異值與閾值相減，篩選出d維大小的主成分，得到量子態(tài)：

(24)

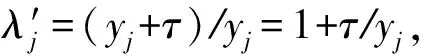
(25)

此時對應原數(shù)據(jù)，得到篩選后的數(shù)據(jù)點以及對應的聚類類別如表2所示：

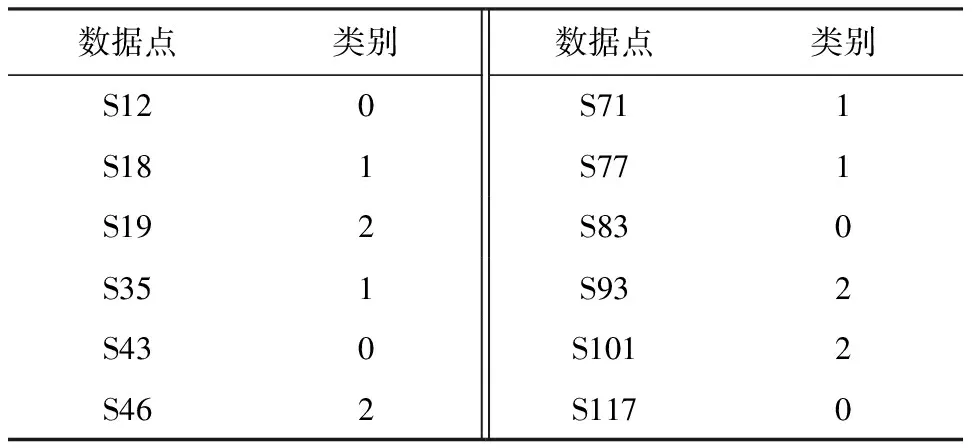
Table 2 Data Points Obtained from Selection

從勢函數(shù)集合中選擇3個最小值作為簇中心ci，i∈{1,2,3}，實驗得出S12、 S35樣本、S93樣本分別為該數(shù)據(jù)集聚類的3個初始簇中心.利用式(20)的指數(shù)距離公式對原始數(shù)據(jù)集進行距離計算，計算出每一個隨機樣本到這3個簇中心的距離.最后采用最小值搜索算法搜索出最小的距離，將此數(shù)據(jù)點分類到該類別中.直到所有樣本數(shù)據(jù)點都計算完成，最終完成數(shù)據(jù)樣本點的聚類分布.圖4為最小值搜索算法的電路設計：

Fig. 3 Circuit of quantum minimum search algorithm圖3 量子最小值搜索算法電路

現(xiàn)有的量子聚類算法采用Grover算法搜索樣本點到簇中心點距離的最小值.當數(shù)據(jù)規(guī)模較小時，Grover算法的成功率不能達到100%.本文在搜索過程中采用的最小值搜索算法[11]基于Grover-Long算法做出改進，提高搜索成功率，并且采用動態(tài)策略降低算法的復雜度，同時優(yōu)化設計電路，縮減門的數(shù)量.

隨著現(xiàn)代通訊科技的快速發(fā)展，信息傳遞模式逐步呈現(xiàn)出多元化特征，而媒體運維的核心仍然是信息的基本內(nèi)容。對于新聞資訊熱點的篩選與信息表達方式的選擇，能夠有效反映一家新媒體的專業(yè)水平。時政新聞在新聞領(lǐng)域發(fā)揮著不可替代的作用，但部分電視媒體缺乏對其應有的重視，甚至膚淺的認為時政新聞的主體內(nèi)容應當局限于領(lǐng)導決策層的重要會議，與基層群眾的根本利益不產(chǎn)生關(guān)聯(lián)。這種理念不僅是對黨政戰(zhàn)略指導方針的褻瀆，也是對民生新聞的曲解。因此，確立宏觀民生新聞理念勢在必行，并且應當從如下幾方面著手。

除此之外，本文在數(shù)據(jù)集統(tǒng)一的情況下，將提出的QC-PCA算法與QC算法、EDQC算法以及文獻[20]提出的NSQC算法在聚類準確度(樣本聚類正確的個數(shù)/總樣本數(shù))上進行比較，結(jié)果如圖4所示.另外，圖5展示的不同算法的聚類效果,圖5(a)表示原始數(shù)據(jù)集樣本點分布及所屬類別，圖5(b)～(e)分別表示QC，EDQC，NSQC以及提出的QC-PCA算法的聚類效果.從圖4可以看出,經(jīng)過10次迭代，4種算法的聚類準確度都趨于收斂，其中QC-PCA算法的聚類準確度最高，為0.78， NSQC算法的聚類準確度為0.75，EDQC算法的聚類準確度為0.74，QC算法的聚類準確度最低，為0.72.圖5(e)代表的QC-PCA算法的聚類效果相對較好，相同類別的數(shù)據(jù)點的顏色相比較于其他聚類算法顯得比較統(tǒng)一，圖5(b)(c)(d)代表的QC，EDQC，NSQC算法的聚類結(jié)果相對較差，相同類別的數(shù)據(jù)點的顏色分布比較凌亂.

Fig. 4 Comparison of clustering accuracy for algorithms圖4 不同算法的聚類準確度比較

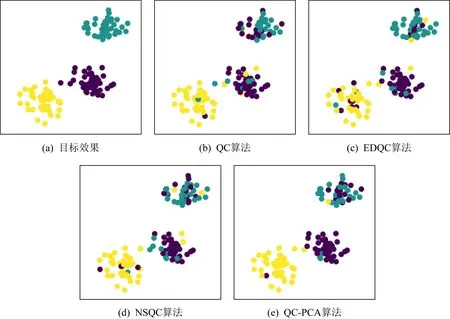
Fig. 5 Comparison of clustering performance for four quantum clustering algorithms圖5 4種量子聚類算法的聚類效果比較

實驗結(jié)果表明，本算法利用量子主成分分析算法對數(shù)據(jù)進行預處理，能夠較為準確地選出具有更多主成分的數(shù)據(jù)點作為簇中心，降低了簇中心的選取對聚類精度的影響.另外，本算法采用優(yōu)化后的量子最小值搜索算法，降低了樣本點之間最短距離搜索的復雜程度.

4 性能評估

本節(jié)分別從簇中心選取和樣本點之間最短距離搜索的時間復雜度以及資源消耗3個方面對提出的QC-PCA算法做出評估.假設存在N個M維的樣本點數(shù)據(jù)，分為K類，迭代次數(shù)為T.

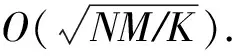
從資源消耗上來看，本文提出的QC-PCA算法與經(jīng)典算法K-Means相比，從原來的O(NM)比特降到了O(logNM)量子比特，與其他量子算法相比，從O(NlogM)量子比特降到了O(logNM)量子比特.表3選取K-Means算法、QC算法、EDQC算法、NSQC算法、QC-PCA算法，從簇中心選取時間復雜度，最短距離搜索時間復雜度和資源消耗這3個方面給出了具體的對比和評估.

Table 3 Complexity Comparison for Different Algorithms

根據(jù)表3可以直觀看出，QC-PCA與傳統(tǒng)算法和其他3個量子算法相比在簇中心選取時間復雜度、最短距離搜索時間復雜度以及資源消耗上均有不同程度的改進效果.

5 總 結(jié)

本文提出了一種針對聚類問題的量子主成分分析算法(QC-PCA算法)，利用奇異值分解的思想，減少異常值對簇中心選取的影響，并采用量子最小值搜索算法尋找距離樣本點最近的簇中心，減少聚類所需迭代次數(shù).仿真實驗表明，QC-PCA算法與已有的量子聚類算法相比，提升了聚類準確度.性能評估表明，QC-PCA算法與已有的傳統(tǒng)算法及量子聚類算法相比，在簇中心選取時間復雜度，最短距離搜索時間復雜度和資源消耗上均有不同程度的改進.

作者貢獻聲明：劉文杰是本研究的構(gòu)思者，指導實驗設計、數(shù)據(jù)分析、論文寫作與修改；王博思是本研究的實驗設計者和實驗研究的執(zhí)行人，完成數(shù)據(jù)分析，論文初稿的寫作；陳君琇參與實驗設計和實驗結(jié)果分析.全體作者都閱讀并同意最終的文本.