基于深度聚合神經網絡的網約車需求時空熱度預測

郭羽含，田 寧

（遼寧工程技術大學 軟件學院，遼寧 葫蘆島 125105）

0 引言

隨著移動設備的普及和互聯網的快速發展，網絡預約出租汽車（簡稱網約車）已成為城鎮居民的主要出行方式之一。選擇網約車出行有利于緩解城市交通擁堵，對提高交通資源的利用、減少環境污染具有積極意義。截至2020 年，滴滴出行、神州專車、首汽約車等大型網約車平臺的用戶規模已達4 億。隨著用戶出行需求的逐年增長，依托上述平臺從事網約車經營活動的汽車駕駛員數量也快速增加。面對數量巨大的服務提供者與用戶需求，平衡供需分布成為網約車平臺亟待解決的問題。若服務車輛分布與乘客分布差異較大，不但會導致乘客候車時間長、對平臺的服務滿意度降低，還會使服務車輛空駛距離增加、運營效率低下、運營利潤減少；若可用服務車輛被提前調配至需求熱度較高區域，則平臺的資源利用率和服務質量可得到顯著提升。

引導服務車輛的前提為預測不同空間位置在不同時間范圍的需求熱度，但需求熱度與時間、空間、環境等多種影響因素相關且動態變化，因此預測難度較高。針對以往的交通問題的預測，現有的研究模型或方法可分為以下四類：

1）基于歷史數據或時間序列的預測模型。

基于歷史數據的預測模型由于維度單一，無法準確反映多維影響因素，故預測準確率較低。基于時間序列的統計模型只能用于數據相對穩定、呈規律性變化的情況，如肖強等［1］利用泊松分布計算出租車的合乘概率和等待時間；Jamil等［2］使用差分自回歸移動平均進行時間序列的分析，預測需求的熱點區域；Moreira-Matias 等［3］把加權時變泊松模型與出租車傳感器數據結合用于預測短期范圍內出租車乘客的空間分布。然而，隨著我國城市建設速度的加快，需求熱點區域的頻繁變化也導致僅憑歷史同期訂單數量無法準確預測當前時空點的需求熱度。

2）基于機器學習的預測模型。

隨著人工智能技術的發展，基于數據的機器學習方法逐漸成為解決短時交通需求預測的主要方法。傳統機器學習方法［4-6］可對更復雜的數據進行建模，捕捉交通信息中更深層次的特征，因此預測準確度也相對較高，如：Zhang等［7］考慮到出租車的需求和供應，提出二次集成梯度提升決策樹方法來預測二者的差距，避免了在不同的數據稀疏條件下帶來的預測結果變差的問題；Jiang等［8］以網約車短期需求預測為目標，提出了一種基于最小二乘基于向量機（Least Squares Support Vector Machine，LS-SVM）的預測方法，并與Lasso 線性回歸、最近鄰回歸、決策樹回歸等算法對比，驗證了其性能的高效性；郭憲等［9］提出基于多源數據的梯度決策回歸樹需求預測方法，基于多元歷史數據，可實時預測當天的下一時間片段內各個城市區域的實時需求。雖然上述三者都考慮了多維影響因素，但仍然較難準確反映復雜多維數據的非線性相關性。

3）基于深度學習的預測方法。

深度神經網絡［10-15］被廣泛應用于需求預測領域且收效良好。Hou 等［16］利用深度神經網絡對不同路段的行駛時間進行了預測，使用單模型結構對交通網絡中的所有路段進行準確的預測，不必為每個路段分別構建自定義模型，從而降低了建模的復雜度；Zhan 等［17］提出了一種基于卷積神經網絡（Convolutional Neural Network，CNN）的交通流預測方法，使用浮動車的GPS 軌跡數據來估算全市的交通量；Yu 等［18］提出了時空圖卷積網絡框架，使用門控循環單元和圖卷積進行了長期交通流量預測；Ma 等［19］提出了一種大規模交通網絡速度預測的深度卷積神經網絡，將時空矩陣轉換為圖像作為CNN 的輸入。后三者都改進了傳統方法中長期預測任務經常忽略時空依賴性的缺點。

4）基于多模型的組合預測模型。

通過將不同的子模型組合，可以發揮每個模型對于不同特征提取的優勢，如段宗濤等［20］使用CNN-LSTM-ResNet（Convolutional Neural Network &Long Short-Term Memory &Residual Network）組合模型對出租車需求進行了預測，采用殘差神經網絡的CNN 框架來分別模擬人群流量的臨近性、周期性和趨勢特征，使用長短期記憶（Long Short-Term Memory，LSTM）網絡學習交通流變化的時空特征，為解決時空序列問題提供了新的思路；Ke 等［21］利用LSTM 神經網絡對天氣等具有時間序列信息的特征進行了提取，再結合卷積LSTM 網絡對時空特征進行了提取，對比其他單個模型實驗，驗證了融合模型的有效性。

綜上可知，將時空數據應用于網約車需求預測中可取得較好成效，但由于不同類別的時空數據存在結構差異性，使用單一結構的模型較難完整捕捉不同結構、不同城市、不同規模時空數據的隱含特征，因此其預測準確度和魯棒性仍有提升空間。此外，由于需求預測還存在空間關聯性和環境關聯性等其他復雜因素，全面完整地利用多維時空數據和深度學習技術對網約車需求進行準確預測仍然非常具有挑戰性。針對上述問題，本文對網約車出行的時空需求進行了形式化定義，提出了一種深度聚合神經網絡（Deep Aggregated Neural Network，DANN）模型以預測不同時空下的需求熱度。通過多個子模型分別學習環境變量、時空變量和空間變量的隱含特征，并將子模型的輸出進行多層次聚合得到最終的預測結果。

1 問題定義

本文以時空需求熱度表示一個空間區域在一段時間范圍內的網約車乘客出行需求熱度，其詳細定義如下。

1.1 基本概念

定義1空間網格。設有給定地理空間區域S，其緯度最大和最小值分別為latmax和latmin，經度最大和最小值分別為lngmax和lngmin，則該空間區域S可被分割為p×q個二維網格，每個網格稱為一個空間網格Si，j，其中i∈[1，p]?N 且j∈[1，q]?N。Si，j的長度hlat=(latmax-latmin)/p，寬 度hlng=lngmax-lngmin。

定義2需求。需求rk=(ek，latk，lngk)為乘客k的網約車出行訂單，其中ek為乘客需要服務的時間（如實時出行則ek為當前時間），latk和lngk為乘客出發地緯度和經度。若latmin+hlat(i-1) ≤latk≤latmin+hlati且lngmin+hlng(j-1) ≤lngk≤lngmin+hlng j，則需求rk屬于空間網格Si，j。

定義3時空需求熱度。將一天的24 h 分割為等長的δ段，每個時段tl(l∈[1，δ] ?N)的長度為24/δh。對于每個空間網格Si，j和時段tl，其相應的時空需求熱度Pij，l可以定義為空間網格Si，j中在時段tl范圍內的需求數量。

1.2 時空需求熱度變量

受時間、區域和天氣條件等多種外部因素影響，城市不同區域需求熱度變化規律復雜；因此，使用單一變量作為模型輸入很難準確預測求密度變化。本文將影響需求熱度變化的變量分為外部環境變量、時空變量和空間變量。在外部環境變量方面，月份、日期、星期、時段、是否為節假日、溫度條件、氣象條件、空氣質量均對出行需求有顯著影響，故上述類別的12 種因子被選為環境變量。相鄰時段、前天同時段、上周同時段的需求熱度被選為時間變量特征。大量不同類別的興趣點（Point Of Interest，POI）信息可從不同層面反映一個空間區域的繁榮程度；因此，本文以12 種POI 的數量作為空間變量。上述特征的定義及其量化取值范圍見表1。

表1 時空需求熱度預測特征Tab.1 Features for spatio-temporal demand heat prediction

基于上述特征，時空需求熱度的預測問題定義如下。

問題1 時空需求熱度預測。根據給定的特征值Xe、Xg和Xs預測tl時刻Si，j區域的時空需求熱度Pij，l，其中Xe=（xmo，xda，xtl，xho，xwe，xtt，xht，xwt，xra，xsn，xfl，xap），Xg=（xms，xjd，xyy，xsc，xly，xjs，xyl，xxq，xxx，xcz，xqy，xzf），Xs=（xlp，xlt，xlw）。

2 模型構建

本文提出的深度聚合神經網絡（DANN）由3 個子單元結構組成，分別為外部環境學習單元的長短期記憶（LSTM）模型、時空特征學習單元的卷積長短期記憶（Convolutional LSTM，ConvLSTM）模型和空間特征學習單元的卷積神經網絡（CNN）模型，其總體結構如圖1 所示。3 個子網絡模型分別處理相應類別的時空數據，并將其輸出經多層聚合獲得最終預測結果。

圖1 DANN結構Fig.1 Structure of DANN

2.1 外部環境特征學習單元

設Xe為外部環境因素的特征向量，由問題1 可知Xe=（xmo，xda，xtl，xho，xwe，xtt，xht，xwt，xra，xsn，xfl，xap）。由于外部環境變量，如日期、節假日、天氣、空氣污染指數等，都具有時間上下文相關性；因此本文采用長短期記憶（LSTM）網絡單元結構來捕捉其在時間維度的依賴關系。LSTM 在處理與時間序列相關的數據時表現優異，可較好處理長距依賴問題，且通過引入3 個門控神經元可有效緩解梯度爆炸和梯度彌散［22］。

LSTM 單元結構如圖2 所示，其內部結構主要由遺忘門、輸入門和輸出門組成。假定當前時刻為t，xt為輸入的外部環境變量向量Xe，yt為輸出狀態值,為記憶單元，pt為輸入門狀態值，dt為遺忘門狀態值，qt為輸出門狀態值。遺忘門根據前一時刻的隱層信息yt-1以及當前時刻的輸入xt，通過激活函數輸出遺忘元素的比率，以及在原始記憶單元中丟失部分信息。輸入門pt通過類似的結構篩選出輸入數據中需保存至記憶單元的數據，并將其與通過遺忘門之后的記憶單元數據相加作為記憶單元的輸出st。最后，隱藏層的數據通過輸出門數據與新記憶單元數據進行逐點相乘計算得到yt。記憶單元的狀態值由輸入門和輸出門共同控制。對于每個時間步長t，迭代計算過程如下：

圖2 LSTM單元結構Fig.2 Structure of LSTM unit

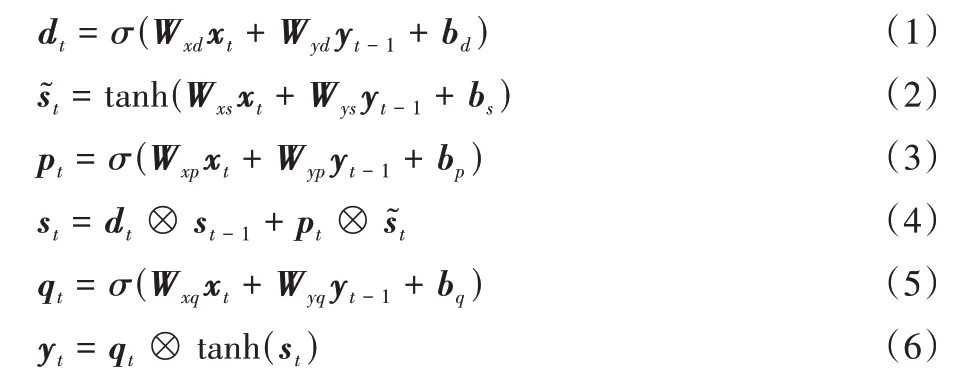
其中：Wx、Wy分別為各單元xt、yt-1對應權重，b為相應偏置。σ(x)和tanh(x)為非線性主動函數，計算方法如式（7）（8）所示：

2.2 時空特征學習單元

時空需求熱度在每日相同時段、每月相同星期存在周期性，因此具有時間自相關性；此外，其空間網格間也具有空間相關性，因此本文采用卷積長短期記憶（ConvLSTM）單元結構［23］來捕捉其在時間和空間維度的依賴關系。ConvLSTM 將LSTM 單元中所有向量轉換為張量，使得LSTM 單元可通過卷積操作進行連接，因此該單元結構既可捕捉時間依賴關系，又可提取空間特征，其結構如圖3 所示。

圖3 ConvLSTM單元結構Fig.3 Structure of ConvLSTM unit

如圖3 所示，ConvLSTM 通過在狀態到狀態和輸入到狀態轉換中實現卷積算子來計算某個網格單元的時空需求熱度。通過t次迭代，每個ConvLSTM 層都可以映射一個輸入的需求熱度張量X=(X1，X2，…，Xt)到一個隱藏層張量H=(H1，H2，…，Ht)。同樣地，堆疊形式的多個ConvLSTM 層會更好地發現需求熱度的時空特征，提高本文模型的預測精度。

由定義3可得tl時段不同區域Si，j的時空熱度Pij，l，令

假定當前時刻為t，Xt表示時空需求熱度輸入張量，Ht表示輸出張量，Ct表示記憶向量，It表示輸入門張量，Ft表示遺忘門張量，Ot表示輸出門張量；?表示Hadamard 乘法；*表示卷積操作；W為卷積核，可提供權重共享。

2.3 空間特征學習單元

本文以區域內POI 數量表述空間特征。需求熱度與區域及其周邊土地利用模式密切相關，POI 涵蓋城市各類設施位置與屬性信息，通過多個卷積層可有效捕捉空間隱含特征，如圖4 所示。由于高層特征圖中的單個節點依賴于中層的多個節點特征映射，依賴于底層（即輸入）中所有節點的特征映射，即多層卷積可捕捉較大范圍內的POI 與需求熱度之間的依賴關系。

圖4 CNN結構Fig.4 Structure of CNN

為緩解卷積過程中損失需求細節，本文設計了一種三通道模式，將原始POI 熱度圖劃分為3 個通道分別進行卷積處理，包括：低密度子圖（只保留POI 數量小于θ的值）、原密度子圖（原始值全部保留）和高密度子圖（只保留POI數量大于θ的值），如圖5 所示。由于不同通道的網絡參數相互獨立，此結構可有效降低密度差異性對預測效果的影響。

圖5 需求熱度圖的通道劃分Fig.5 Channel partition of demand heat map

2.4 子網絡單元聚合

圖6 展示了不同日期和不同時段需求總數量的變化情況，可以觀察到該值存在周期性波動：在月范圍內呈多峰狀態，在日范圍內呈現單峰狀態。這表明時空熱度受到近周期片段、日周期片段和周周期片段的影響，但影響程度存在著差異；同樣地，對于空間變量，劃分的不同通道對時空熱度也存在著不同影響，因此本文采取了基于參數矩陣的融合方式來調整時空熱度受不同因素的影響程度。

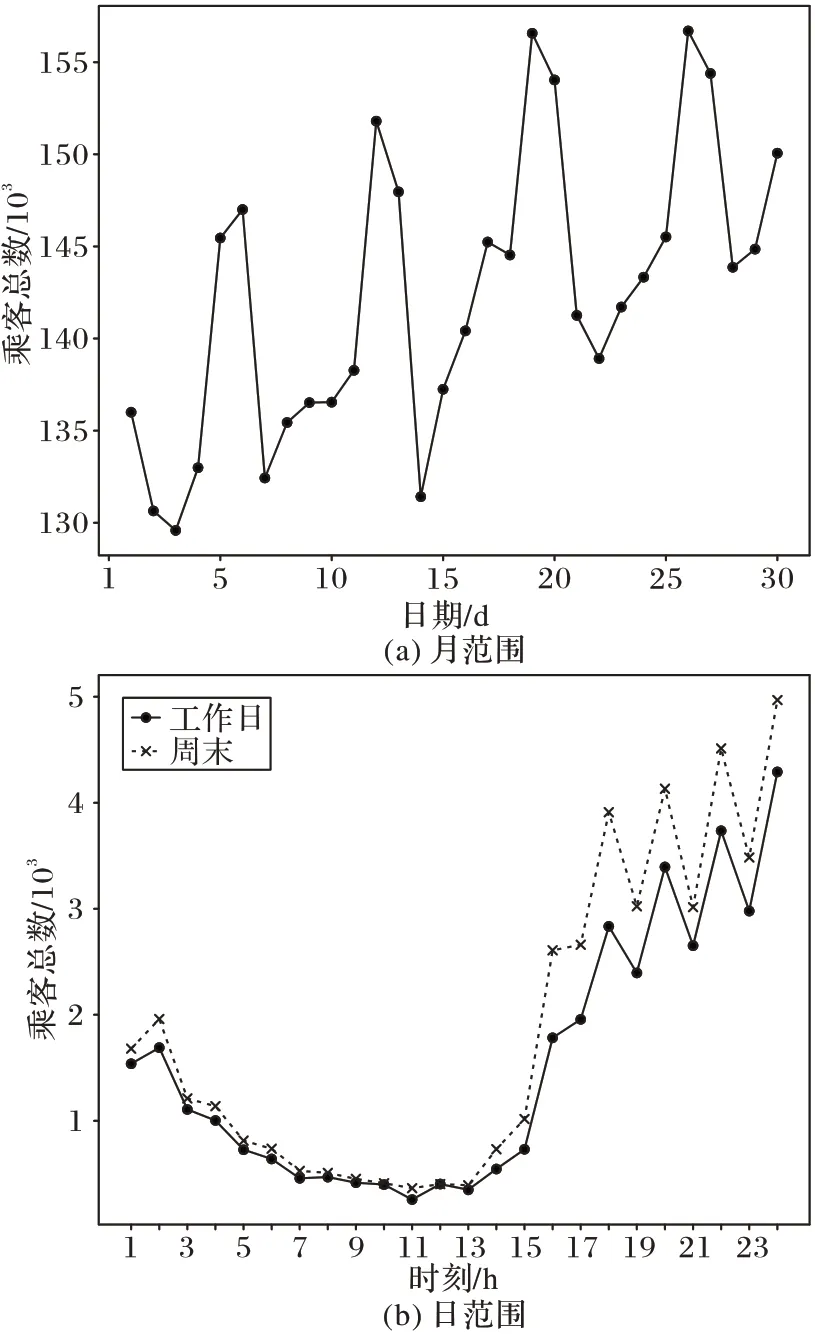
圖6 乘客總數量變化示例Fig.6 Examples of total passenger number change

分別將時間特征學習模型的輸出和空間特征學習模型的輸出以基于參數矩陣的方式融合，如式（15）（16）：

其中we、ws、wg為融合權重。

2.5 模型訓練

模型訓練的目標為使預測值與真實值Pt的均方誤差（Mean Squared Error，MSE）最小化，從而獲得上述全部權值w的最優取值。目標函數如式（18）所示，其中加入L2 范式正則化項以避免過度擬合，α為平衡參數。模型訓練流程如算法1 所示。

算法1 模型訓練流程。

3 實驗與結果分析

本文基于真實數據進行了實驗，對算法的預測精度和參數靈敏度進行了驗證，實驗環境見表2。

表2 實驗環境Tab.2 Experimental environment

3.1 數據源和算法參數設置

實驗數據源基于滴滴蓋亞數據開放計劃，采用成都市、西安市和海口市城市區域網約車訂單數據，POI 數據通過百度地圖應用程序編程接口（Application Programming Interface，API）獲取，時空網格劃分及乘客分布如圖7 所示，數據集具體參數如表3 所示。

圖7 區域劃分及乘客分布示例Fig.7 Example of region division and passenger distribution

表3 數據集參數Tab.3 Dataset parameters

利用Keras 深度學習框架實驗，優化器為Adadelta，DANN 訓練參數設置標準為最優預測精度，模型主要結構具體如表4 所示。

表4 中Conv3D 為3D 卷積層，Conv 為2D 卷積層，Maxpool為最大池化層，激活函數如式（19）所示：

表4 DANN訓練參數Tab.4 DANN training parameters

3.2 模型預測精度分析

本文將DANN 與下述8 種模型進行對比，各算法參數設置標準為最優預測精度，其具體值如下。

由于對比模型與本文中使用的特征及數據存在差異，為保證對比的公平性，對比模型進行了部分修改以保證與本文模型的對比條件一致。實驗采用均方誤差（MSE）、平均絕對誤差（Mean Absolute Error，MAE）、R-平方（R2）和可釋方差（Explained Variance Score，EVS）作為評價標準，對比實驗結果見表5。

由表5 可見，本文模型在上述3 個數據集的4 種指標中均取得最高精度。從整體上來看，由于傳統的機器學習算法（即前4 個模型）建模能力有限，考慮的影響因子較少，因此誤差較大，3 個數據集的R2平均誤差分別為22.83%、21.77%和27.01%；而深度學習算法（即后5 個模型）相較機器學習算法在3 個數據集上的預測結果上有著較大提升，R2平均誤差分別為12.69%、9.43%和13.80%。相較于LSTM，ConvLSTM 在建模時加入了空間特征的提取，因此表現優于前者，R2在3 個數據集上分別提升0.030 7、0.026 3和0.059 2。與FCL-Net模型和HDLN-Net 模型相比，DANN 在加入了空間維度POI 后，可較大幅度提升模型的預測能力，因此準確度優于前面兩種方法。與區域預測模型相比，DANN 的優勢在于空間特征提取時采取了3 個子模型分別卷積再融合的方式，緩解了卷積過程帶來的細節損失，提升了預測的準確度。此外，在時空特征的提取上，本文采取了子模型再融合的方式分別處理了近周期時空圖、日周期時空圖和周周期時空圖，因此DANN 在利用環境變量、時空變量建模的情況下提取到更多有效隱含特 征，其預測精度優于其他對比模型。

表5 實驗結果對比Tab.5 Comparison of experimental results

圖8 展示了真實時空需求熱度（T）與DANN 預測值（P）的對比結果。圖中以灰度表示時間需求熱度的差異，較深的顏色代表較高的熱度。從圖中可以觀察到，預測熱度與真實熱度高度一致。此外，由圖8 可知，午高峰時段的需求強度顯著高于睡眠時間的需求強度，且需求強度在空間上不平衡，部分網格的需求強度顯著高于其他網格的需求強度。隨著時間的推移，需求強度在不同的網格變化較明顯，使得需求強度預測難度增加，而本文模型結合不同的變量捕獲時空特征可以有效解決這個問題。

圖8 真實值與預測值的對比Fig.8 Comparison between predicted and real values

3.3 子模型預測結果分析

為更加直觀觀察不同子模型以及單子模型和多子模型融合后對預測結果帶來的影響，以成都數據集為例，在本節對不同的子模型預測結果進行了分析，評價方式同3.2 節，結果如表6 所示。

表6 不同子模型對比實驗結果Tab.6 Experimental results comparison of different sub-models

由表6 可見，聚合模型DANN 的R2分別比時空特征學習單元（多模型）、空間特征學習單元（多模型）和外部環境特征學習單元這3 個子模型提高2.63%、12.78%和6.22%，說明聚合模型在預測結果準確度上優于單個子模型。由于聚合模型利用了不同子模型對不同特征提取的優勢，因此達到了更好的預測效果；此外，多子模型融合的結果也優于單子模型，說明基于周期的時空變量和基于圖像點值的空間變量劃分方法也提高了預測的準確性。

3.4 不同天氣下的預測結果比較

為探究不同天氣下DANN 的預測結果，將測試樣本分別按照天氣類型和空氣污染指數等級進行分類，計算各類別預測結果的評價值（R2、EVS、MAE 和MSE），得出不同天氣條件下的預測精度，其中，空氣污染指數分為5 個等級：優、良、輕度污染、中度污染和重度污染，評價結果如表7、8 所示。

表7 不同天氣類型下的預測結果Tab.7 Prediction results under different types of weather

由表7 可見，DANN 在大雨天氣條件下的誤差較大，而在其他天氣條件下的波動較小，這說明時空需求在極端天氣條件下的變化規律更為復雜。由表8 可見，DANN 在各個空氣質量等級的條件下預測結果都較為穩定，誤差未出現大波動。綜上所述，DANN 在不同的天氣類型和空氣質量等級下的預測效果均較為穩定且精度較高，因此可用于不同天氣條件下的時空需求預測。

表8 不同空氣質量等級下的預測結果Tab.8 Prediction results under different air quality classes

3.5 模型靈敏度影響分析

以成都數據集為例，對本文模型的結構和參數進行了分析。圖9（a）顯示了迭代次數對實驗精度的影響。如圖9（a）所示，R2在初期顯著增加，然后趨于平緩，說明該網絡最開始有較高的收斂速度，隨著訓練次數的增加達到平穩狀態，而訓練40～80 次的效果差異性較小。

圖9（b）展示了網絡層數的影響：隨著網絡層數增大，模型的R2 先增大后減小，說明網絡層數越深預測效果也會越好；但當網絡層數過深時，模型會變得很復雜，這時往往容易出現欠擬合現象，因此預測效果逐漸變差。卷積視野的范圍由所使用的卷積核大小決定的。在這里改變卷積核的大小從2×2 到5×5，從圖9（c）可以看到，3×3 的卷積核具有較高的R2，表明其具有更好的空間依賴建模能力。從圖9（d）中可以看出卷積核數量為128 時得到的結果更好。

圖9 參數調整與靈敏度分析Fig.9 Parameter adjustment and sensitivity analysis

最后，對多步預測進行了敏感度分析，圖10 表明，R2的最小值高于0.86，優于其他對比模型。同時，R2的值緩慢下降，沒有出現較大波動，表明該方法可以較好地適應多步預測任務。

圖10 多步預測敏感度分析Fig.10 Sensitivity analysis of multi-step prediction

4 結語

本文為準確預測網約車需求，針對差異化結構的多維數據，提出了一種深度聚合神經網絡模型。該模型綜合考慮了環境變量、時空變量等多維影響因素，提出了基于周期的時空變量和基于圖像點值的空間變量劃分方法；依據數據特點構建了不同的子神經網絡結構并提出了多種異類子神經網絡的聚合方法及聚合權重的設置方法。本文模型可作為網約車需求預測的有效手段，預測結果可有效解決服務車輛與乘客間的供需不平衡問題，提升服務車輛的運營效率和利潤，同時降低乘客等待時間并改善其對服務平臺的滿意度；但需要指出，深度學習模型對訓練數據量要求較高，且其預測結果的因果可解釋性存在一定限制。未來研究將通過優化模型網絡結構進一步提升預測能力，并探索具有更好可解釋性的機器學習方法。