基于強化迭代學習的四旋翼無人機軌跡控制

劉旭光，杜昌平，鄭 耀

（浙江大學 航空航天學院，杭州 310027）

0 引言

四旋翼無人機（quadrotor）作為最為經典的無人機（Unmanned Aerial Vehicle，UAV）結構，因其結構簡單、穩定性強主要被應用于航拍、勘探等領域。穩定準確地對目標軌跡進行跟蹤是完成一系列復雜任務的基礎，所以如何在現有控制架構的基礎上進行優化，實現跟蹤精度的提升有重大的研究價值。

針對軌跡跟蹤精度指標的優化方法，國內外研究人員出了各種不同的優化方法。Rosales 等［1］提出了一種自適應比例-積分-微分（Proportional-Integral-Derivative，PID）控制的方法，通過神經網絡對六軸無人機系統進行系統辨識，以反向傳播輸出誤差來調整PID 增益，從而達到減小誤差的目的，但是由于神經網絡在線進行系統辨識需要大量復雜計算，導致了算法的可用性降低。另外基于自適應整定PID 的思路，研究人員引入了遺傳算法、線性二次型調節器（Linear Quadratic Regulator，LQR）控 制、模糊控 制、強化學 習（Reinforcement Learning，RL）等方法［2-6］來調整PID 控制器的參數；由于是對無人機反饋控制系統的PID 控制器直接進行調整，各種算法帶來的計算負擔將對算法的實時性產生較大影響。為了避免對無人機傳統控制結構改良帶來的負面效果，一部分研究人員摒棄了傳統的無人機控制架構轉而引入諸如滑模變結構控制（Sliding Mode Control，SMC）［7-10］、無模型強化學習控制［11］等方法。劉小雄等［12］應用DQN（Deep QNetwork）算法對無人機高度及水平位置控制器進行優化，高度及水平位置控制器由兩個不同的神經網絡來構建，神經網絡參數通過強化學習算法進行優化，優化后的網絡參數的控制器保證了無人機的跟蹤精度。滑模變結構控制方法同樣存在著較大的弊端，即在滑模面附近的抖振現象，存在抖振的控制輸入作用到作動器上勢必導致作動器高頻的動作變換，從而極大降低無人機的壽命。而強化學習由于需要大量的數據支撐以及長時間的數據分析處理，在實時性上很難滿足飛行控制需求，難以應用于無人機實際飛行控制中。針對以上問題，一種前饋的學習控制方法——迭代學習控制（Iterative Learning Control，ILC）逐漸得到重視，它可以作為傳統反饋控制器的前饋環節嵌入無人機的飛行控制系統中，具有可移植性強、精度高、算法結構簡單等特點。Ma 等［13］提出了一種由比例-微分（Proportional-Derivative，PD）控制器組成的迭代學習控制器的方法來控制四旋翼飛行器在恒定高度上遵循相同的軌跡，算法結構簡單，能夠便捷地移植到飛行器的控制系統中，但是該方法PD 存在控制器參數整定困難的問題。Dong 等［14］基于PID 型迭代學習控制器引入了一種新的控制律，即通過模糊控制的方法整定控制器中的學習參數，消除了不確定因素對系統的影響，也降低了參數整定的難度；但模糊控制較為依賴專家經驗，使得該方法難以得到大范圍的推廣應用。綜上，目前無人機軌跡控制研究主要分為兩個方向：一是經典控制方法，這類控制方法往往需要對控制系統及環境建立精確的模型，而往往復雜的飛行環境及高度非線性系統無法進行精確建模，導致經典控制方法的精度無法提升，對于經典飛行剖面的歷史飛行信息無法進行利用，同時抗干擾性較差；二是智能控制方法，該方法不需要精準的控制系統建模，可以利用神經網絡對非線性系統進行模擬，但是往往需要大量數據和大規模的計算，難以在線應用，同時由于完全摒棄了傳統控制結構，單純的神經網絡控制在主流飛控平臺上可遷移性較差。

綜上所述，經典反饋控制方法中存在精度難以提升、抗干擾性差、難以實現靜態穩定等問題；而不依賴模型的智能控制架構則需要大量數據計算來對整個系統模型進行模擬，實時性較差。本文將兩種控制方法進行融合，以經典反饋控制系統架構為基礎，引入迭代學習前饋控制環節解決傳統反饋控制具有時滯及難以實現靜態穩定的問題；并且在前饋控制器中，將強化學習與迭代學習控制算法相結合，提出強化迭代學習控制（Reinforcement Learning-Iterative Learning Control，RL-ILC）算法。該算法依靠強化學習強大的大范圍內最優值搜索能力來整定迭代學習中學習律參數，使得迭代學習能夠更精細準確地在小范圍內利用典型飛行剖面的歷史飛行信息與環境信息進行迭代學習，對系統的前饋控制輸入進行進一步的細致優化。在保證迭代學習控制器在未知環境噪聲干擾下保持收斂的同時提高其迭代速度，使得系統可以更快實現對目標軌跡的完美跟蹤。

1 無人機系統模型

1.1 系統動力學模型

本文主要參考DJI 公司生產的450 mm-1.5 kg 型號的四旋翼無人機［15］。無人機系統模型主要為無人機動力學模型和無人機控制系統模型兩部分。其中，無人機槳翼產生的升力分析在機體坐標系中進行［16］，槳翼產生升力fi的計算公式如下：

其中：CT為單槳綜合拉力系數，ω表示槳翼的轉速。機體系下無人機的總升力FT為：

不考慮風阻的情況下，在地理坐標系中對無人機平動的三軸加速度進行計算，記航向角、俯仰角、滾轉角分別為φ、θ、γ。進一步可得地理系下無人機平動三軸加速度如下：

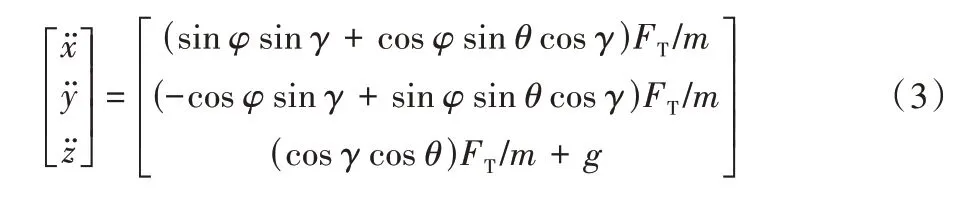
其中：x、y、z分別表示地面坐標系中x、y、z軸的位移分量。定義轉動慣量J，可得無人機的姿態角加速度如下：

其中：ΔJij=Jii-Jjj，Fi，j=fi+fj(i，j=x，y，z)。假設無人機系統控制輸入的4 個分量分別對應U1=FT，U2=f2-f4，U3=f1-f3，U4=F2，4-F1，3，代入上述模型中可得無人機系統的動力學模型如下：

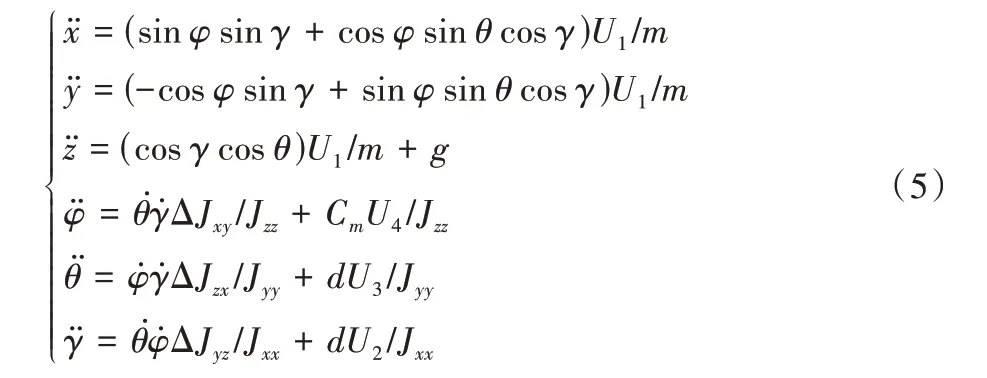
其中部分參數在表1 中進行說明注解。

表1 四旋翼無人機的部分參數Tab.1 Some parameters of quadrotor

1.2 控制系統模型

傳統的飛行控制系統多采用PID 控制算法，單獨的反饋控制器會給系統帶來很大的時延，這使得系統無法實現快速跟蹤。當環境中存在較大的環境噪聲時，反饋控制器的時延會導致被控系統容易出現在穩態附近振蕩的現象，從而帶來無法達到控制精度的問題。引入前饋控制器與反饋控制器組成前饋-反饋控制系統可以提升系統的時間響應特性，抑制環境擾動。本文在經典的無人機反饋控制結構的基礎上增加了使用迭代學習控制算法的前饋控制器，控制系統的結構示意圖如圖1。

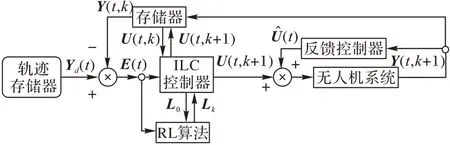
圖1 無人機控制系統結構Fig.1 Structure of UAV control system

U(t，k+1)中的k表示迭代域內當前的代數；L0及Lk均為學習參數矩陣，前者對應迭代學習控制器中的學習參數矩陣的初始值，后者對應經過強化學習（RL）算法優化后的第k次迭代時學習參數矩陣；Yd(t)表示在t時刻預設理想軌跡的值；E(t)表示在t時刻軌跡誤差值。

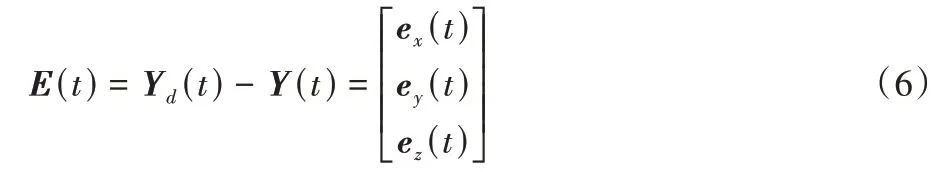
計算得到的誤差E(t)的各個分量用于計算反饋控制器的輸出(t)中的分量(t)，計算方法如式（7）：

2 迭代學習控制方法

迭代學習控制最早由日本學者提出并應用于機械臂的運動控制中，控制精度極高。對于類似機械臂這類運動具有周期性的系統，迭代學習算法可以不斷對每個周期內的運動軌跡的誤差進行學習，而后在時間域內修正控制輸入。在迭代域內不斷重復直至實現在有限時間內對軌跡的完美跟蹤。在無人機軌跡控制領域存在一些典型的飛行剖面具有學習價值，同時空中也存在反復出現且無法精準測量和預知的干擾。傳統的前饋控制器無法對重復未知干擾給出相應的補償也無法利用典型飛行剖面的歷史飛行信息，所以普通前饋環節并不能保證理想的系統輸出。本文中的前饋控制器采用迭代學習控制方法對典型的飛行剖面進行學習，能夠充分利用歷史飛行數據不斷學習，排除未知環境噪聲的影響，在有限時間內最大限度地提升對典型飛行剖面的跟蹤精度。

四旋翼無人機系統作為經典的非線性欠驅動系統，系統的狀態量之間耦合性很強，所以在進行分析解算時需要針對不同的任務需求對系統進行相應的簡化分析。本文的控制任務是在存在未知擾動Dr的環境下令飛行器跟蹤一段著陸軌線Yd=[xd，yd，zd]T。假設無人機進行小角度ε(ε=φ，θ，γ)機動，即cosε≈1，sinε≈ε，εi·εj≈0，令=-g，無人機系統模型可以簡化為式（8）形式：

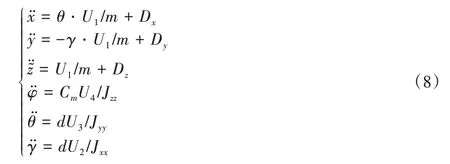
其中：Dx、Dy、Dz分別為未知時變擾動Dr于特定時刻在3 個軸向上的分量。由式（8）可知系統輸入僅可以由輸入直接控制，縱向及橫向加速度受U3和U2的間接控制。為了減小控制系統的相對階數得到目標與輸入的直接關系，將理想軌線之于縱向x及橫向y的加速度要求轉移到俯仰角θ和滾轉角γ的角加速度上。期望姿態角的計算公式如下：

對期望位置軌跡的跟蹤可以轉換為對期望姿態角(θd，γd)以及期望高度zd的跟蹤。

根據式（8）及式（9）確定系統狀態變量、系統輸入量、系統輸出量如下：

系統的動力學模型可以重寫為系統的狀態方程如下：

其中：A∈R6×6、B∈R6×3、C∈R3×6分別為系統的狀態矩陣、輸入矩陣以及輸出矩陣［17］，矩陣中的參數可以對照表1 中參數計算得到，矩陣D為全0 陣。

本章提出的迭代學習控制算法為PD 型迭代學習控制（PD Iterative Learning Control，PD-ILC）算 法，控制器結構如下。

如圖2 所示，迭代學習控制系統由3 個迭代學習控制器及若干存儲器構成。由于X向與Y向控制器同時與姿態角和控制輸入U1相關，3 個控制量之間存在耦合，故在每個迭代周期內，先令X向與Y向控制器同時進行優化計算確定當前迭代中的θd與γd；更新后的U2(k+1)、U3(k+1)輸入到被控無人機系統中得到用于Z向迭代學習控制器的Z向誤差ez(k)；最終Z向控制器完成對U1的更新，將得到的U1(k+1)、U2(k+1)與U3(k+1)輸入無人機系統得到下次迭代周期的誤差E(k+1)，開始下一次迭代。

圖2 迭代學習控制系統結構Fig.2 Structure of iterative learning control system

決定迭代學習控制器控制精度的主要因素包括初始控制輸入以及學習律。本文選擇的學習律是經典的PD 學習律，即以本次迭代當前時刻的軌跡誤差與軌跡誤差的導數信息來更新下次迭代相同時刻的控制輸入，設計X、Y、Z三向的迭代學習控制律如下：

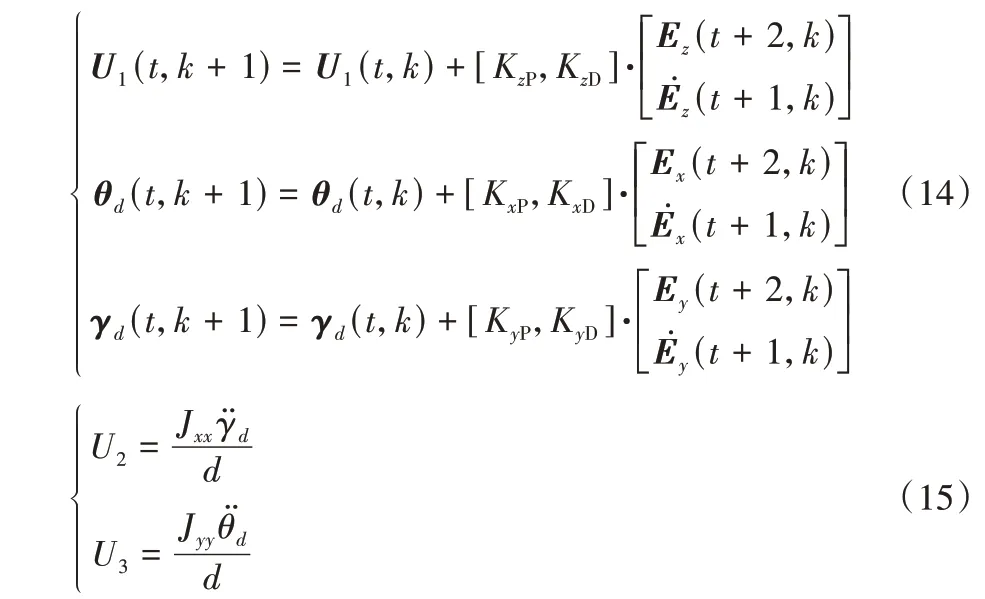
其中：Ei(t，k)、(t，k)分別為第k次迭代中t時刻的軌跡誤差值及其導數，KP及KD則依據下標分別對應3 個軸向迭代學習控制器的學習參數。由于未知擾動的存在，式（9）無法通過計算求解，故采用迭代學習方法尋優。將得到的最優姿態角按照式（15）進行反解即可得控制輸入U2、U3。

通過上述推導可知，控制輸入Ui直接作用的狀態量是加速度或角加速度，其作用到位移或角度上是存在時延的，時延問題在所有的高相對階系統中都存在。為了減弱控制滯后帶來的負面影響，本文在經典的PD 學習律的結構上進行修改，用順延2 個時間步長的誤差量以及順延1 個時間步長的誤差的一階導數來更新當前時刻的控制輸入，實驗結果顯示此種設計在一定程度上減小了控制滯后的影響。

3 基于強化學習的參數整定方法

PD 型迭代學習控制算法的核心是學習律中PD 的參數選擇，不合適的參數選擇無法保證算法的收斂性，不同學習參數下算法的收斂速度以及受噪聲的影響也大不相同。迭代學習控制算法的學習參數選擇多為李雅普諾夫法結合專家經驗進行選擇，需要對模型及環境進行精準建模才能保證算法的性能。Q-learning 算法作為一種典型的無模型強化學習算法，不需要明確的模型，通過智能體與環境的不斷交互即可得到最優策略，非常適合應用于類似PD 參數整定的這類狀態空間不大且環境簡單的任務中［18］。本章提出一種基于強化學習Q-learning 算法的PD 學習律參數整定方法，與前文迭代學習算法相結合，解決傳統的PD-ILC 算法存在的學習律參數選擇困難的問題。

基于強化學習Q-learning 參數整定方法中涉及的主要對象包括：智能體Agent 為無人機控制系統的迭代學習控制器；環境E為無人機系統；狀態空間S，其中的每個狀態s∈S，s=[KP，KD]T；動作空間A，其中每個動作a∈A，a=[ΔKP，ΔKD]T；R為獎勵值。算法的基本思想如下：

選取迭代學習控制器中的兩個學習律參數KP、KD作為狀態，在該狀態下采取的動作為ΔKP，ΔKD，則對應的狀態轉移計算公式為：

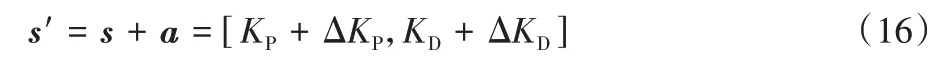
動作選擇策略π則采用“ε-貪心策略”：

獎勵函數的設置會在很大程度上影響模型的訓練效果［19］。針對迭代學習控制最基本的精度目標，在獎勵中設置如下指標：

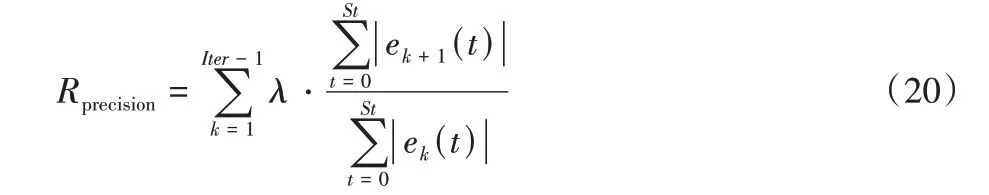
式（20）（21）中：α和β均為正常數，St表示仿真時間，Iter表示迭代次數。將不同次迭代的軌跡誤差和的收斂情況與獎勵值大小相關聯，篩選出在保證迭代過程收斂的同時能用盡可能少的迭代完成收斂的學習參數。另外在實際應用過程中，除了對精度和收斂性的要求外，對于單次飛行過程中無人機跟蹤軌跡的快速穩定追蹤指標也有要求。參照精度指標的設計思路，對無人機軌跡控制穩定時間的獎勵函數設計如下：

式（22）（23）中：ε和χ均為正常數，τ(k)表示第k次迭代過程中跟蹤誤差穩定在0.05 m 以內的起始時間。如果在當前的學習參數下穩定起始時間能隨著迭代逐次降低，則給予該參數穩定時間獎勵RStable，且該獎勵值與優化效果成正比。所以最終的獎勵函數為：

確定Q-value 的更新方法及獎勵函數的設計方法后，進行算法的整定工作，算法流程如下。

4 實驗與結果分析

為了檢驗本文設計的強化迭代學習控制（RL-ILC）算法對于經典著陸飛行軌線的跟蹤性能以及在存在未知擾動的環境中的魯棒性，在Matlab 中進行仿真實驗并與未經學習參數尋優的傳統迭代學習控制（ILC）算法、經典PID 控制算法及滑模控制（Sliding Mode Control，SMC）算法的軌跡控制結果作對比。假設無人機在著陸任務初始時懸停于高度120 m的空中，著陸時速度為0 m/s。綜合以上幾點要求，設置標準著陸軌跡的Z向分量Zd為：

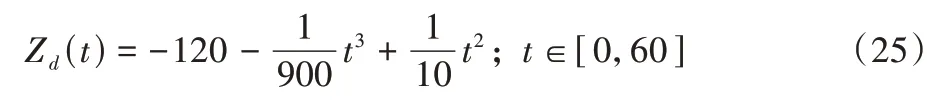
橫側向分量Yd為：

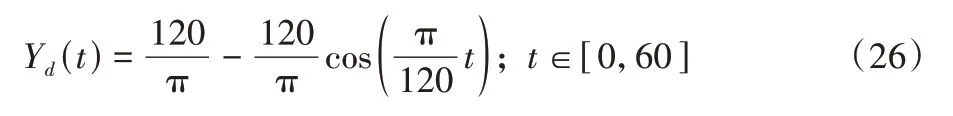
縱向分量Xd為：

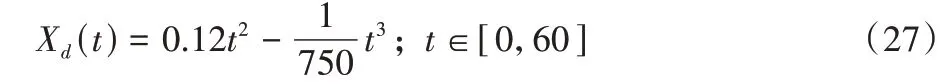
如式（25）～（27）所示仿真時間設定為60 s，計算步長為0.01 s，使用歐拉法進行數值積分。輸入變量及部分狀態變量對應初始參數見表2。

表2 輸入變量初始參數Tab.2 Initial parameters of input variables

表2 中的初始參數為第一次仿真過程中的恒定值，不隨時間變化。實驗過程中不涉及航向角變化故設置航向角φ及對應的角速度以及輸入U4數值均為0。強化學習整定的初始學習參數為（0.6，0.9），以此為起點進行學習參數的優化。

通過大量數據實驗，最終得到的Q-table 經過處理后，由圖3 將強化學習尋優學習參數的過程以散點圖的形式呈現。不同的(KP，KD)組合有不同的Value 值，Value 值與前文的獎賞值正相關，即收斂性好、收斂速度快的學習參數組合有更高的Value 值。按照Value 值的大小即可篩選出此狀態下的最優學習參數。

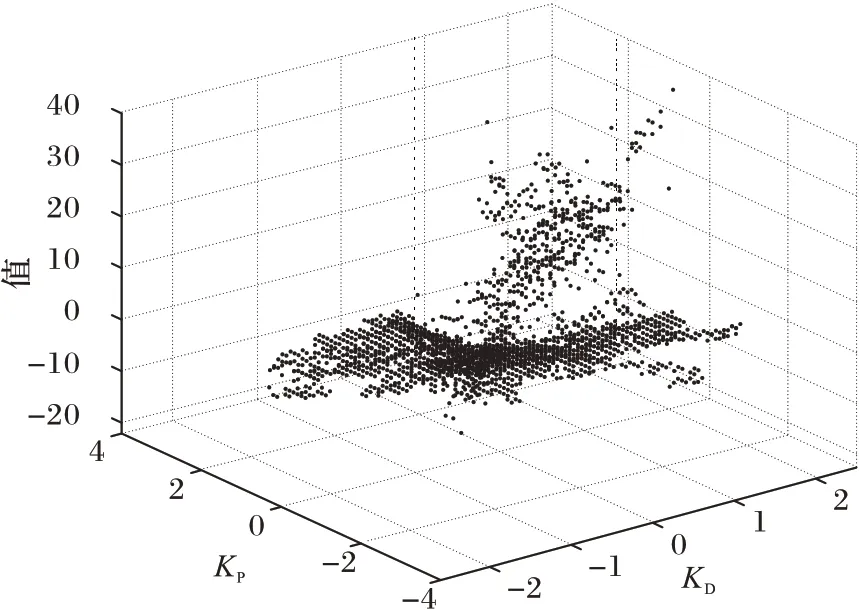
圖3 強化學習參數尋優散點圖Fig.3 Scatter diagram of reinforcement learning parameter optimization

圖4（d）表示強化學習尋優學習參數前后仿真時間內軌跡誤差的絕對值之和隨著迭代次數的變化示意圖，經過強化學習優化后的學習參數在收斂速度上優化顯著。未經參數優化的迭代學習選取的初始學習參數不佳導致總誤差隨迭代次數增加而增大，即軌跡控制發散；而通過強化學習優化后，僅需要2～3 次迭代即可將總誤差縮減至初始誤差和的0.2%，滿足總體誤差要求。

圖4（a）～（c）則從時間域角度出發，分別展示了在有隨機噪聲存在的情況下4 種控制算法的縱向位移X，橫向位移Y以及高度向位移Z這3 個自由度上的位置量隨時間的變化；圖4（e）為實驗設置的隨機噪聲；圖4（f）則是4 種不同算法下三維運動軌跡與理想軌跡之間的對比。從時間域角度來看，由于噪聲的存在，優化學習參數后的迭代學習算法輸出的實際軌跡在目標軌跡附近略有波動，但波動均十分微小，跟蹤效果優異。與之相比，未經參數優化的普通迭代學習算法在任務初期有明顯的波動效果；且由于參數性能較差，算法并不能保證收斂，導致軌跡誤差進一步發散。通過將未經參數優化的方法迭代20 次的結果與優化后的方法迭代10 次的結果進行對比，不難發現不良的學習參數帶來的誤差即使通過增加迭代次數來進行補償也未能帶來明顯的改善。另外兩種傳統的飛行控制算法，在存在未知擾動的環境下也存在軌跡跟蹤效果較差的問題。PID 算法在有擾動的情況下容易在目標軌線出現波動，軌跡誤差較大且沒有隨時間增長收斂到理想軌跡的趨勢。SMC 算法相較于PID 算法，其收斂性更好，能夠收斂到理想軌跡附近，抗擾性略優于PID 算法；但相較于RL-ILC 算法，SMC 算法的調節時間較長，無法在有擾動的情況下快速響應完成調節。綜合來看，經過強化學習算法尋優后的參數能夠實現環境自適應，在不同的環境中自適應進行參數調節保證迭代學習算法的快速收斂以及軌跡跟蹤的精準度。

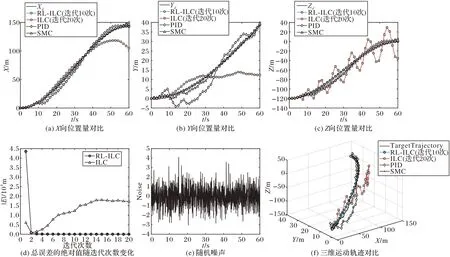
圖4 強化迭代學習與迭代學習的軌跡跟蹤對比Fig.4 Trajectory tracking comparison between reinforcement learning-iterative learning and iterative learning

5 結語

本文針對經典PID 控制系統下四旋翼無人機軌跡跟蹤特定飛行軌跡時存在精度較差的問題，提供一種新的解決方法：在經典的反饋控制結構中加入迭代學習前饋控制器，通過不斷對典型的飛行剖面進行學習，優化控制器輸入來逐漸減小軌跡誤差，從而實現完美追蹤。RL-ILC 與ILC 的對比實驗結果顯示，迭代學習控制器中的學習參數選擇對控制效果的影響較大。通過引入強化學習Q-learning 算法優化迭代學習控制律的學習參數，解決了迭代學習算法學習參數選擇困難的問題。在不同的環境以及任務下，強化學習強大的學習搜索能力能在保證迭代學習算法快速收斂且達到最優控制效果的同時，降低系統對環境的依賴性，從而大幅提升算法的抗干擾性、穩定性和實用性。最后的仿真實驗結果也顯示優化學習參數后的迭代學習算法在存在較大的隨機環境噪聲的情況下仍可實現接近完美的軌跡跟蹤。在今后的實驗研究中，可以考慮將該控制方法應用于實際飛行中，利用實際飛行數據來進一步優化控制算法。