可穿戴傳感器的人體活動能量預測模型研究

王 琳，孫 倩，馬曉娜，高永艷，劉 毅，馬宏偉，楊東強+

1.山東建筑大學 計算機科學與技術學院，濟南 250101

2.山東建筑大學 體育部，濟南 250101

隨著智能生物技術（intelligent bio-technology，IBT）和可穿戴技術（wearable technology，WT）的日趨融合，由體力活動而產生的運動能量消耗，即人體活動能量消耗（physical activity energy expenditure，PAEE）計算研究成為移動計算領域的一個熱點問題[1-2]。通過準確預測PAEE能夠掌握其身體活動水平，有的放矢地指導其科學運動，為制定膳食推薦標準提供支持，并可廣泛應用于運動健身、養老醫療、體能訓練、慢性病預防治療等方面[3-5]。在人體運動能量檢測中，氣體代謝分析法和運動加速度器測量法是兩種主要的計算方法。

計算PAEE的典型處理流程包括五個步驟，如圖1所示[1]。首先捕獲人體被試佩戴的傳感器所獲得的原始信號，然后從表征原始信號的原始傳感器測量值中提取不同的時域或頻域的特征（如均值、方差、主頻等信息）。采用特征提取方法（互信息、相關系數等）選出有效特征，作為評估或建立PAEE 模型算法的輸入。從簡單的線性回歸到復雜的機器學習技術（如彈性網絡、人工神經網絡和支持向量機等）[6-7]，都可以用來訓練估計模型（如圖1中的決策樹模型或多層感知機模型），從傳感器新獲得的數據就可用訓練好的模型進行PAEE估計。一般情況下，實驗過程中通過氣體代謝分析儀測量的能量消耗[8]，可以作為PAEE估計的黃金標準值。

圖1 基于傳感器的PAEE典型處理流程Fig.1 Typical PAEE processing flow of sensor

研究表明，PAEE 評估主要存在三方面的問題：第一，傳感器類型和傳感器的佩戴位置影響了PAEE估計的精度。第二，如何提取更為有效的特征。傳統方法多采用三軸加速度器的COUNTS值作為主要參數，簡單但不夠精確。可以從傳感器信號提取時頻域的特征，提高預測精度。第三，融合方法不能只采用傳統的線性回歸方法，可采用機器學習方法融合不同的技術，提高PAEE估計精度。

針對以上問題，本文從以下四方面展開工作：

（1）在數據預處理階段，由于傳感器信號的時效性和周期性，通過傅里葉變換生成FFT特征，對于三維原始速度數據使用正弦函數進行曲線擬合，并進行顯著性差異檢驗后再進行數據分析，去除無效和冗余數據，保證數據的有效性。

（2）實驗數據采用帶抖動的數據集作為測試數據，模擬真實情況下的數據，準確估計PAEE 估計模型的泛化能力。

（3）數據融合方法，Schuldhaus等[9]提出的一種傳感器融合的PAEE估計方法，對每個傳感器源分別進行數據預處理、特征提取和回歸分別生成估計PAEE值，然后對預測結果取平均值，進行決策級融合。此種方法因為采用平均值，降低了預測精度。采用通過特征選擇選出少量特征，比較多種模型估計PAEE值的性能指標，選擇出最優模型。

（4）本研究采用基于WEKA 的實驗平臺[10-11]，利用相關系數、互信息、包裝方法和嵌入方法的四類特征選擇方法選取特征，并使用多線性回歸、回歸樹、支持向量機和神經網絡四種機器學習方法估計PAEE值。決策級融合時用最優策略選取評估模型。

1 實驗數據預處理

該數據集通過采集人體所佩戴的加速度傳感器和陀螺儀傳感器獲得。在臀部和腳踝上分別放置一個三軸加速度計（HPA，AKA）和一個三軸陀螺儀（HPG，AKG）均為SHIMMER 傳感器（Shimmer Research，Dublin，Ireland）。每次測試包括三種速度等級，分別是3.2 km/h、4.8 km/h 和6.4 km/h，傳感器的采樣率為204.8 Hz。采用MET 表示消耗的能量，用氣體代謝分析儀測定耗氧量，采樣率為0.2 Hz，實驗指標如表1所示。在跑步機上，10個受試者進行了兩次實驗，一次實驗為正常狀態下跑步，另一次實驗使用了振蕩狀態下的跑步。

表1 實驗參數Table 1 Experimental parameters

1.1 人體運動能量預測的主要特征

首先要分析提取傳感器哪些特征以及如何處理這些特征，PAEE 預測常用的特征可以分成時域特征、頻域特征、時頻域特征以及統計與測量特征四大類[12-13]。時域特征（如表2所示的均值和Counts值等）使用比較廣泛，但其受噪聲數據的影響較大。對信號的時域到頻域轉換的過程中，最常用的技術是快速傅里葉變換（fast Fourier transform，FFT），提取到的常用頻域特征包括主頻、振幅和光譜熵等（如表2所示）。統計與測量特征由于個體差異較大，通用性不強，在本實驗中沒有采納。

表2 PAEE中的常用時域頻域特征Table 2 Time-domains and frequency-domains characteristics of PAEE

對于每個傳感器，提取的27個特征包括：絕對信號振幅的均值、標準差、第10 分位點、第25 分位點、第50 分位點、第75 分位點和第90 分位點、最小值和最大值等。在此基礎上，又加入了每個傳感器的協方差、counts（計算方法參考式（1））、主頻（計算方法參考式（2））。其中時域特征counts 的計算方法如式（1）所示：

其滑動窗口設置為1 024，即取連續1 024個數據。頻域特征中主頻使用傅里葉變換來計算，采用式（2）進行計算。對傅里葉變換結果進行分析后發現，信號主頻對應的最大振幅的系數代表了人體活動強度水平。考慮到人體運動能量集中在實數部分，因此只取實數部分，并取前100項的最大值作為特征值。

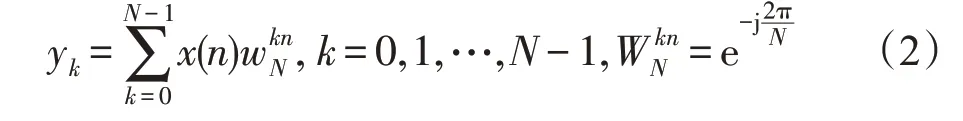
1.2 顯著性差異檢驗（T檢驗）和方差分析

由于運動過程中的傳感器佩戴位置、測量誤差、能量代謝儀出問題等因素可能造成數據偏離，首先需要對9 個樣本進行顯著性差異檢驗，可以用T 檢驗來檢測樣本偏離程度。對實驗數據在3 個速度（3.2 km/h、4.8 km/h 和6.4 km/h）等級下采樣。在對3個數據集進行處理之前，采用正弦函數進行曲線擬合的處理方法[14-15]對數據集進行預處理。

采用如式（3）所示的正弦函數進行數據擬合，其中參數的取值分別為：a=6.4，b=4.8，c=3.2。

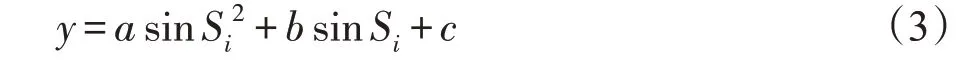
其中，若xi、yi、zi分別表示X、Y、Z三軸的加速度值，則Si可以表示為：

y值與均值進行方差分析，實驗結果中其F值不小于0.05，則說明數據集不存在顯著性差異。按此方法對所有數據集進行顯著性差異檢驗，發現所有數據均不存在顯著性差異，能夠進行后續的數據分析。兩名被試者的比較數據如表3所示。

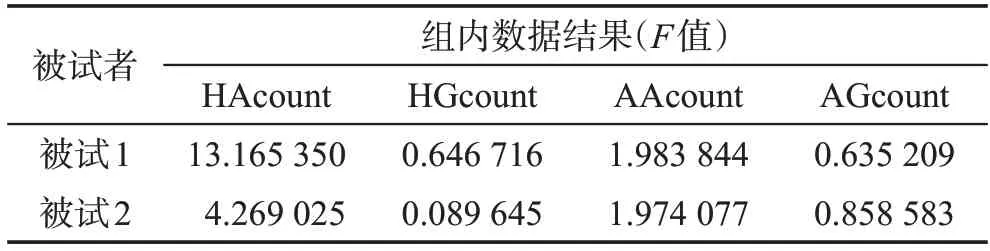
表3 顯著性差異檢驗結果Table 3 Significant difference test results

2 實驗設計

2.1 選擇評估方法

實驗數據集[10]分為兩部分，一部分從正常跑步機獲取，另一部分從振蕩跑步機獲取。正常跑步機產生的數據稱之為正常數據，振蕩跑步機上產生的數據稱之為抖動數據。若在正常數據上使用交叉驗證法，可以取得較高的模型性能評估指標。但考慮到訓練模型需要應用在實際場景中，用正常數據作為訓練集，而用抖動數據作為測試集進行模型的構建與評估，檢驗模型在特征選取后的泛化能力。

2.2 選擇特征選擇方法和機器學習方法

預處理階段所選取的時頻域特征數量非常多，而且可能存在線性相關性。首先采用特征工程對這些特征進行過濾。特征選擇[16-17]可以將高維數據降為低維數據的同時，保留原始主要特征。從特征子集評價準則的角度，特征選擇方法可以分為過濾式（filter）、封裝式（wrapper）以及嵌入式（embedded）方法。評價函數的選擇采用距離度量、信息度量、相關系數度量等方法。特征選擇可以采用人工特征選擇與線性回歸方法相結合，或過濾式特征選擇與線性和非線性回歸方法相結合，或包裹式特征選擇與線性回歸方法相結合，或直接使用嵌入式特征選擇的方法：Lasso回歸算法和Elastic回歸算法[18-20]。本文分別采用了相關系數特征選擇方法、互信息特征選擇方法、封裝特征選擇方法和嵌入式特征選擇方法進行特征選擇，并將其與多線性回歸、回歸樹、基于POLY 函數和RBF（radial basis function）函數的支持向量機、神經網絡等五種機器學習方法相結合進行實驗比較，選出最優模型[21]。

3 實驗結果及分析

采用相關性（correlation coefficient，CC）和平均絕對誤差（mean absolute error，MAE）作為模型評估指標。依次比較相關系數特征選擇方法與多線性回歸、決策樹、支持向量機和神經網絡算法結合的模型的CC 和MAE，互信息特征選擇方法與多線性回歸、決策樹、支持向量機和神經網絡算法結合的CC 和MAE，包裝方法（wrapper）特征選擇與多線性回歸、決策樹、支持向量機和神經網絡算法結合的CC 和MAE，直接使用嵌入式特征選擇的方法Elastic 回歸算法的CC和MAE。

3.1 采用相關系數的相關性測量方法的比較

過濾式特征選擇中，相關系數體現了特征與結果之間的線性依賴關系，其計算方法見式（5）。

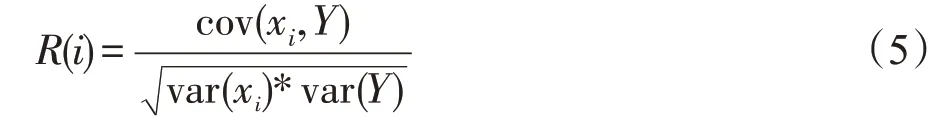
其中，var(xi)是方差，cov(xi,Y)是協方差。

用相關系數方法選取的特征有HA1_prc_10、HA1_prc_25、AA1_prc_50、AA3_CV、AA2_prc_75、AA3_prc_25，分別是腰部加速度計、腳部加速度計的數據，采用多線性回歸進行PAEE 估計，實驗結果如表4所示。從數據結果可以看出，加速度計的特征與能量預測相關性更強，進行特征選擇后相關系數有所提高，平均絕對誤差下降明顯。

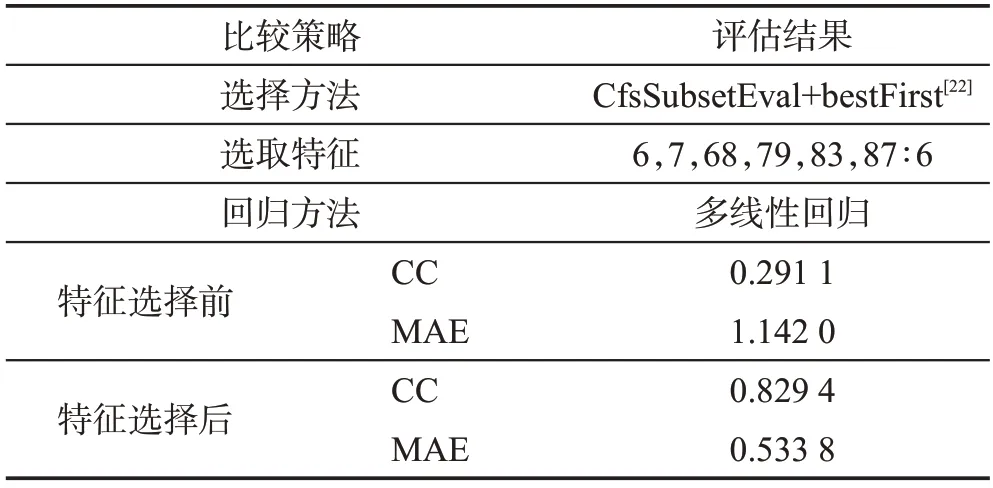
表4 特征選擇前后的評估結果比較（相關系數）Table 4 Comparison of evaluation results before and after feature selection(correlation coefficient)

另外分別用REPTree算法[23]（決策樹算法之一）、POLY多項式核函數的支持向量機算法、RBF徑向基核函數的支持向量機算法、神經網絡算法進行實驗比較，其結果如圖3所示。圖3中MLR指多線性回歸算法，REPTree 是決策樹算法之一，SVM（poly）是代表采用poly 核函數的支持向量機算法，SVM（RBF）是代表采用RBF核函數的支持向量機算法，NN（10,5）表示神經網絡算法。

神經網絡模型采用模型為多層感知機，兩個隱層，其中第一層為10個節點，第二層為5個節點。如圖2 神經網絡連接圖所示，其中參數設置：學習率（learning rate）設為0.3，動能（momentum）設為0.2。

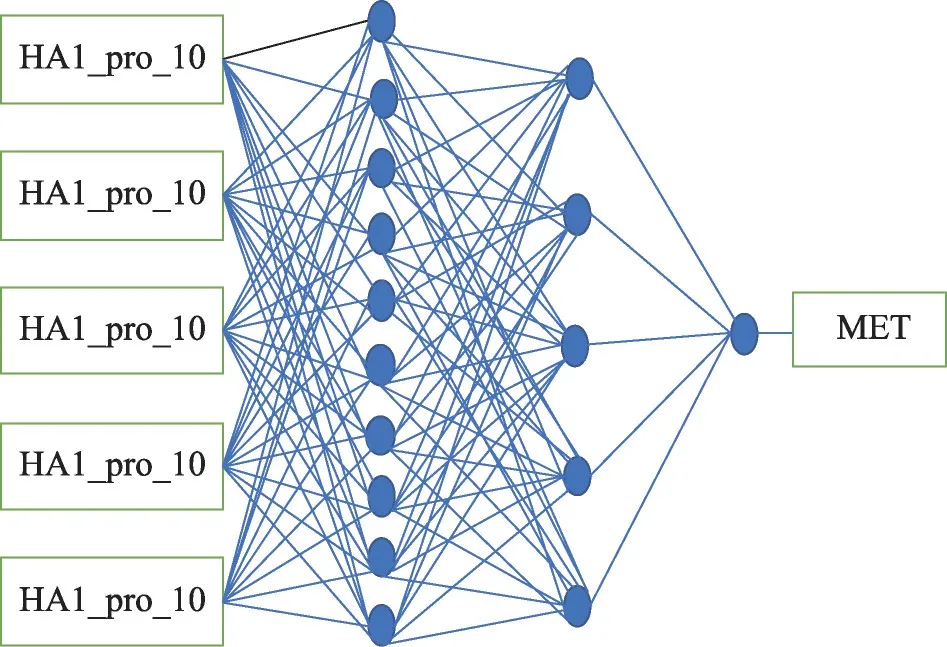
圖2 神經網絡模型連接圖Fig.2 Neural network model connection diagram

圖3表明神經網絡的相關系數最高，平均絕對誤差最低，PAEE 估計效果最好。效果最差的是REPTree算法，相關系數最小，平均絕對誤差最高。

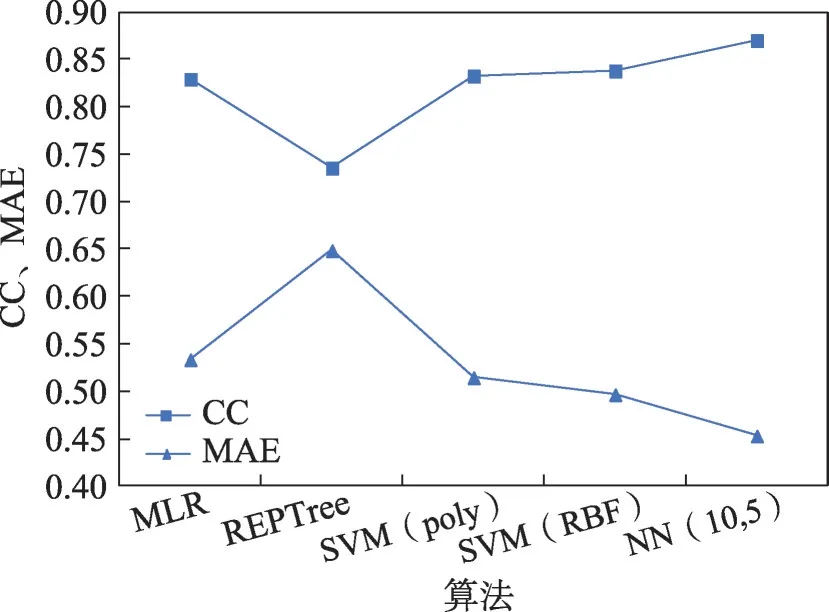
圖3 相關系數選擇特征的評估結果Fig.3 Evaluation results of correlation coefficient selection feature

3.2 采用互信息的信息測量方法比較結果

過濾式特征選擇中，互信息反映的是兩個特征之間的依賴關系，可以由式（6）計算得出。

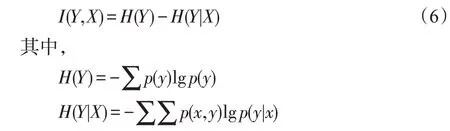
若MI=0 則說明兩個特征是獨立的，若MI ＞0 則說明兩個特征是相互依賴的。由于實驗取得的特征數據是連續值，要計算互信息，必須離散化數據。計算特征之間的互信息后，再根據互信息值進行排序，選取前20個特征如表5所示。

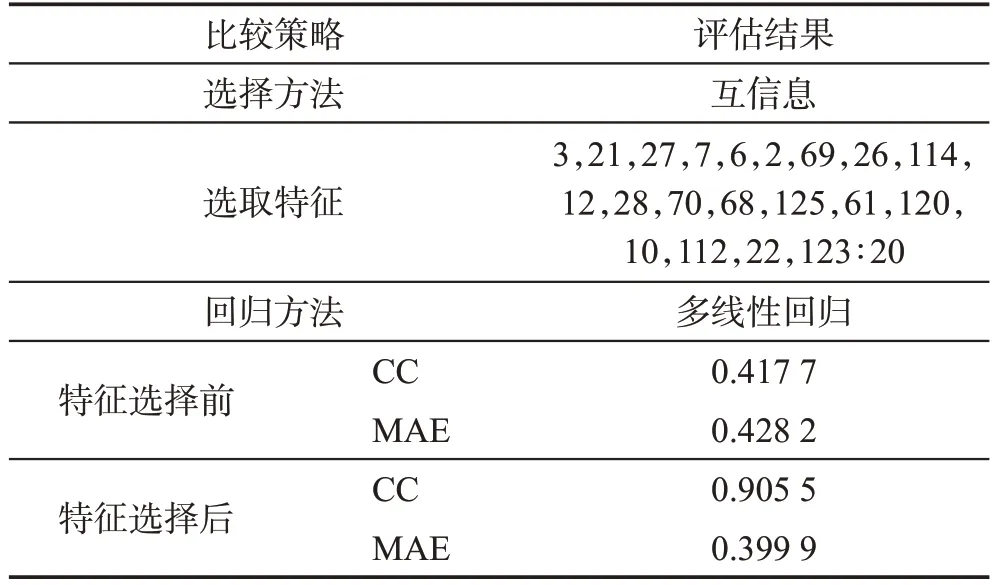
表5 特征選擇前后的評估結果比較（互信息）Table 5 Comparison of evaluation results before and after feature selection(MI)

特征選取后，采用多線性回歸進行PAEE 估計。通過互信息所選出的特征比較多，主要是腰部加速計的特征。除了分位點特征外還包括Counts和陀螺儀的第三軸的特征等。實驗結果表明進行特征選擇后相關系數有所提高，平均絕對誤差有所下降。

采用互信息進行特征選擇后，仍然分別用REPTree算法、SVM（poly）算法、SVM（RBF）算法、神經網絡算法進行實驗，其結果如圖4所示。從實驗結果可以看出，采用SVM的方法得到的結果最好，兩種不同核函數對實驗結果影響不大。由于采用RBF核函數的支持向量機方法比較耗時，由實驗結果可以看出采用POLY核函數的支持向量機方法是最優的。

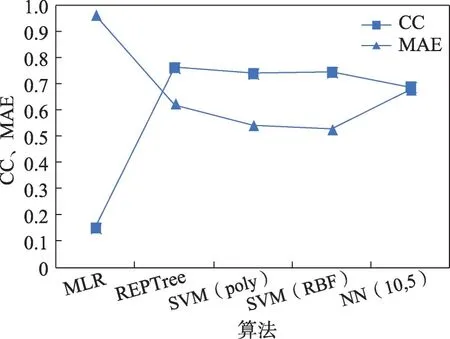
圖4 互信息選擇特征的評估結果比較圖Fig.4 Comparison chart of evaluation results of mutual information selection feature

3.3 包裝方法（wrapper）

特征選擇方法中，包裝方法將預測過程看成一個黑匣子，用性能作為評估的目標函數。采用多線性回歸進行PAEE估計，實驗結果如表6所示，實驗結果表明使用包裝方法特征選擇后相關系數有較大提高，平均絕對誤差下降比較大。

表6 特征選擇前后的評估結果比較（包裝方法）Table 6 Comparison of evaluation results before and after feature selection(wrapper)

同樣地，分別用REPTree算法、SVM（poly）算法、SVM（RBF）算法、神經網絡算法進行實驗，測試結果如圖5所示。使用SVM（RBF）算法的相關系數最高，平均絕對誤差最低。

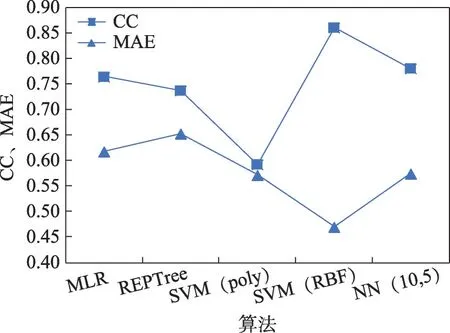
圖5 包裝方法選擇特征的評估結果比較圖Fig.5 Comparison chart of evaluation results of wrapper selection feature

3.4 嵌入式（embedded）方法

嵌入式方法采用邊訓練邊選擇的方法來減少計算時間，是數據特征選擇時效率比較高的方法之一。采用經典的彈性網絡（elastic net）[24]回歸估計PAEE值，使用式（7）計算。

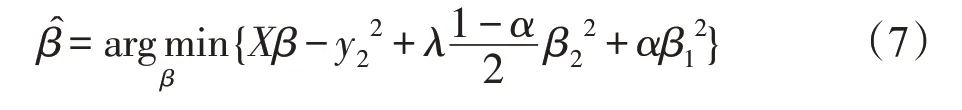
其中，系數α稱為懲罰項，采用廣義交叉驗證最小化的方法確定α的值，計算后將其設置為0.378 5。

PAEE中主要以代謝當量（metabolicequivalent，MET）表示能量消耗，因此可以得到彈性網絡回歸模型：

實驗結果如表7 所示。其相關系數和平均絕對誤差的值與前面的方法比較來看，性能有所提高。選擇的特征是AG3_CV、HG_counts、HG_fft、AG_counts、AG_fft，主要包括陀螺儀的數據，即變異系數和counts、傅里葉變換的值。

表7 嵌入式方法（彈性網絡）評估結果Table 7 Evaluation results of embedded method(elastic network)

與互信息的特征選擇方法比較，該方法所選出的特征數量明顯下降；與包裝方法相比，性能結果與神經網絡相近，但其計算速度比包裝方法快。

將四種特征選擇產生的實驗結果進行比較，所得比較結果如圖6 所示。圖中，CC+NN 表示相關系數方法+神經網絡算法、MI+SVM 表示互信息方法+支持向量機算法、wrapper+SVM表示包裝方法+支持向量機算法、embedded+Elastic 表示嵌入式方法的彈性網絡[25]。

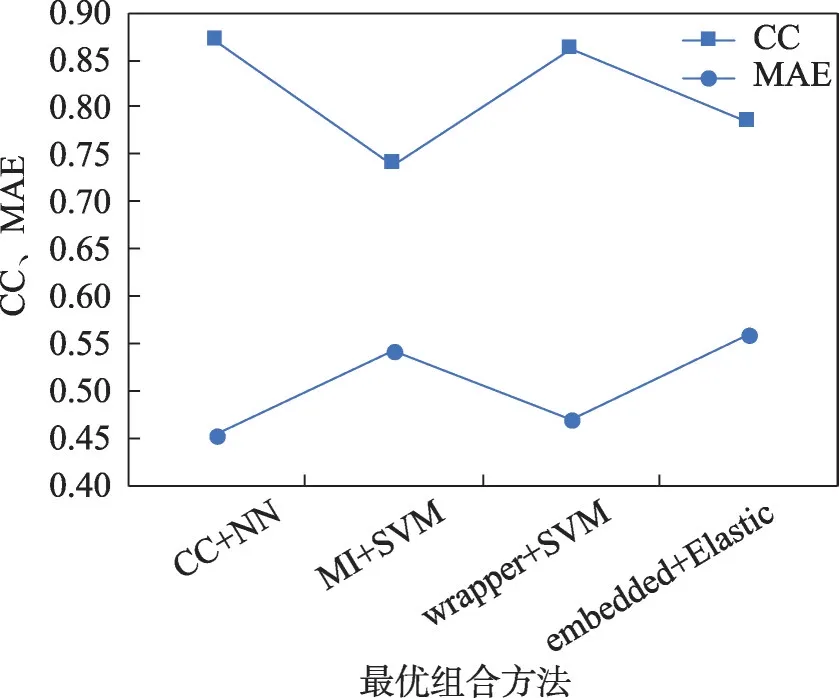
圖6 最優組合方法評估結果比較圖Fig.6 Comparison chart of evaluation results of optimal combination method

本文使用特征方法選擇出來的特征與機器學習算法結合進行數據分析后發現（如表8所示），在人體運行能量消耗預測中，這4個模型效果比較接近。互信息方法的性能相對較差，主要原因是對數據進行了離散化處理，降低了數據的精度。嵌入式方法在許多文獻中都認為是比較好的方法，但在本實驗中并沒有發現它能極大地提高性能。包裝方法的性能不錯，但是在實驗過程中非常耗時。基于相關系數方法的神經網絡算法是所有的結果中最好的，說明神經網絡算法在此類回歸問題上具有較好的效果。

表8 最優組合方法評估結果匯總Table 8 Summary of evaluation results of optimal combination methods

3.5 決策級融合獲得最優數據模型

PAEE 中主要以代謝當量MET 表示能量消耗。構建的PAEE 回歸系統如圖7 所示，嘗試不同的特征選擇方法和機器學習算法組合，最后進行決策級融合。使用最優策略（MAE最小，CC最高）選出最優算法模型預測的MET作為最后的預測結果。

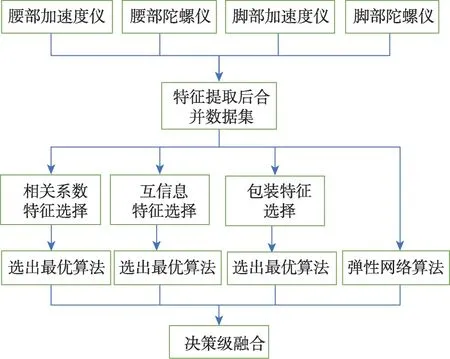
圖7 PAEE 回歸系統Fig.7 Proposed regression system for PAEE

通過決策級融合，得到最優的數據模型：基于相關系數方法和神經網絡算法[26]的PAEE模型。

先用相關系數方法進行特征選擇選出有效特征為HA1_prc_10、HA1_prc_25、AA1_prc_50、AA2_prc_75、AA3_CV、AA3_prc_25，分別代表腰部加速度計、腳部加速度計數據，加速度計的特征比陀螺儀的特征在人體運動能量預測中占有更重要的作用。

4 總結

本文對提取的人體運動能量預測特征使用機器學習的特征選擇方法選出重要的特征[27-28]，使用機器學習的算法構建預測PAEE的數據模型，取得較好的預測效果。通過特征選擇方法，將129 個特征降到6個，極大地提高了神經網絡的訓練速度。同時，采用帶抖動的數據模擬真實數據集，避免了數據的過擬合。基于相關系數和神經網絡算法的PAEE 預測模型可為商用手環或智能手機預測人體運動能量提供參考。