快速3D-CNN結合深度可分離卷積對高光譜圖像分類

王 燕，梁 琦

蘭州理工大學 計算機與通信學院，蘭州 730050

高光譜圖隨著高光譜遙感技術的發展，新的高光譜傳感器能夠同時采集光譜特征和空間特征的連續圖像[1]。高光譜圖像含有豐富的地物特征，包括光譜特征和空間特征。因此，在農業、環境監測、城市規劃和軍事偵察等領域有著廣泛的應用[2]。因為高光譜圖像具有三維立體圖像的屬性，所以為了更好地獲得地物信息，可以充分利用空間和光譜的聯合特征進行圖像分類[3]。但是高光譜圖像在描述了豐富的地物細節信息的同時，也出現了數據之間的高度相關，引起數據的大量冗余問題[4]，增加了計算的復雜度。因此，減少光譜數據間的冗余量，降低數據維度并且提取高光譜圖像的空譜聯合特征成為高光譜圖像分類中的首要任務[5-6]。

深度學習算法的提出，讓高光譜圖像的分類方法有了新的進展。深度學習算法被研究者廣泛運用到高光譜圖像的分類中，取得了良好的研究成果。2014 年，將深度學習網絡SAE（stacked autoencoder）運用到高光譜圖像的分類中，并提出了一種融合光譜特征和空間特征的深度學習模型，得到了較高的分類精度[7]，相繼越來越多的深度學習模型被研究者應用。2015年，將深度置信網絡（deep belief network，DBN）模型引入到高光譜圖像分類中，同時結合了主成分分析的方法（principle component analysis，PCA）對數據進行降維預處理。對特征進行分層學習和采用邏輯回歸的方法對高光譜圖像的空譜特征進行提取，取得了良好的分類效果[8]。2015 年，第一次將卷積神經網絡（convolutional neural networks，CNN）模型應用到高光譜圖像分類中，但是建立的CNN 模型只能進行光譜特征的提取[9]。2016 年提出了一種基于CNN的深度特征提取方法，并建立了一種基于三維卷積神經網絡的深度有限元模型，以提取高光譜遙感圖像的空譜特征，獲得較高的分類精度[10]。2017 年，提出了頻譜空間殘差網絡（spectral-spatial residual network，SSRN），SSRN 中的殘差剩余塊使用恒等映射來連接其他的3D卷積層，便于梯度的反向傳播，同時提取更深層次的光譜特征，緩解了其他深度學習模型存在的精度下降現象[11]。2019年，通過自適應降維，提出了一種用于頻譜空間HSIC（hyperspectral image classification）的半監督三維卷積神經網絡來解決維數詛咒問題[12]。這些研究成果表明基于深度學習的方法在高光譜圖像分類方面取得了一定的成果。但是基于深度模型的方法通常存在過擬合的現象，這是因為在利用深度模型的方法進行訓練的時候需要大量帶標簽的數據，但是高光譜圖像帶標簽的樣本不足。因此，為了盡量避免這樣的問題，需要合適的卷積模型，既能充分發揮卷積神經網絡的巨大優勢，又能減少可學習的參數，從而緩解過擬合問題以及對于訓練樣本數據量的需求。現有的卷積模型較復雜，網絡的參數量大，帶來計算復雜的問題。需要有更加輕量型的卷積網絡來滿足計算時間、效率以及內存的要求。

為了解決上述問題，提出了一種新的快速3DCNN（3-dimensional convolutional neural networks）結合深度可分離卷積的方法。該方法首先將高光譜立方體圖像分割成相同大小的重疊三維小立方體。利用三維卷積核函數對這些小立方體進行處理，生成多個連續波段的三維特征圖，以保留空間和光譜的聯合信息，為特征提取過程提供豐富的空譜信息。使用增量主成分分析（incremental principal component analysis，IPCA）對數據進行預處理，獲得比較重要的波段信息。然后將預處理的數據輸入到3DCNN模型中，在三維卷積對空譜特征同時提取后，加入深度可分離卷積對空間特征再次進行提取以獲得更加豐富的空間特征信息，最后采用Softmax分類器進行分類。相對于其他2D/3D-CNN 模型，所提模型涉及的參數更少，同時運算速率也相對較高，可以獲得較高的分類精度。本文的模型實驗對比了幾種典型的HSIC方法。最后的實驗和比較結果表明，本文所提模型方法性能優于其他比較的方法。

1 基礎理論

1.1 三維卷積神經網絡

早期CNN 模型的建立是針對二維數據設計的，可以對二維形狀進行很好的識別，在目標識別[13]、圖像分割[14]等方面有很好的應用效果，但是對三維立體形狀進行識別分析時就有一定的局限性。研究的高光譜圖像不同于一般的二維圖像，它由空間維和光譜維共同構成，形成三維的數據立方體。在空間維也包含大量的信息，二維卷積神經網絡（2-dimensional convolutional neural networks，2D-CNN）對高光譜圖像的空間特征可以較好地提取，但是不利于同時提取像元的光譜和空間特征[15]。利用卷積神經網絡對高光譜圖像進行分類時，首先要對數據進行降維、去噪等預處理操作，但是降維操作可能會引起高光譜圖像中細節信息的丟失，對高光譜圖像分類造成影響。

針對二維卷積神經網絡對三維高光譜數據的信息利用不足的問題，可引入三維卷積神經網絡對高光譜圖像的空譜特征同時提取。三維卷積神經網絡（3D-CNN）與二維卷積神經網絡（2D-CNN）的網絡結構非常類似，兩類結構都是由基本的卷積層和池化層組成。關鍵的不同之處在于3D-CNN 結構采用的是3D 卷積核來對圖像進行卷積操作。如圖1 所示2D-CNN 和3D-CNN 卷積操作的示例，N×N代表卷積核大小，三維比二維多了M代表的光譜維度大小，L為卷積層輸出通道。3D-CNN在空間維和光譜維上同時進行運算，從而同時提取圖像的空譜特征。不會單獨地提取某一類特征引起特征提取不足，導致分類結果不理想。

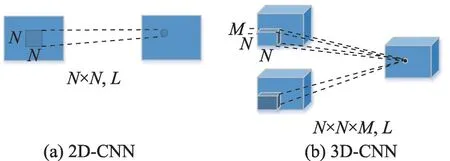
圖1 2D-CNN和3D-CNN算法Fig.1 Algorithm of 2D-CNN and 3D-CNN

三維卷積神經網絡的卷積核在長、寬和通道三個方向上移動，計算神經網絡第i層第j個特征圖在(x,y,z)處的點值V，計算公式如式（1）所示：

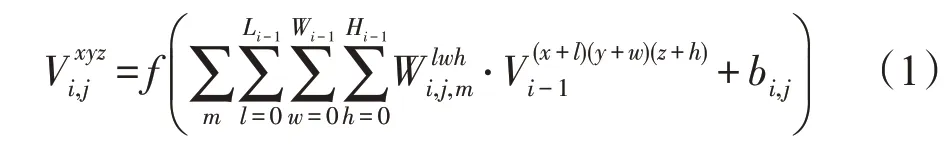
式中，m表示第i-1 層中與當前特征圖相連的特征圖；x與y表示卷積核的長度和寬度，z表示卷積核在光譜維度上的尺寸；W代表與i-1 層相連的第m個特征圖的連接權值；b表示第i層第j個特征圖的偏置，f為激活函數。

1.2 深度可分離卷積

深度可分離卷積（depthwise separable convolution，DSC）[16]是普通二維卷積神經網絡的一種變換形式，可以替換普通二維卷積神經網絡[17]。核心思想就是將普通N個通道為M的卷積拆分成1個通道為M的卷積，該卷積進行單通道濾波操作，區別于普通卷積濾波后通道相加和N個1×1×M的卷積。圖2（a）所示為普通的卷積神經網絡，由卷積層、批歸一化操作和激活函數構成。圖2（b）所示為深度可分離卷積，它是由一個卷積核大小為3×3 的卷積層、批歸一化、激活函數和卷積核大小為1×1 的卷積層、批歸一化、激活函數構成，即分為深度卷積（depthwise convolution）和逐點卷積（pointwise convolution）兩部分[18]。在對多個輸入通道執行常規2D卷積中，卷積核的通道數與輸入的通道數一致。

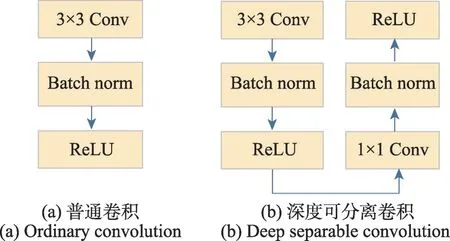
圖2 普通卷積和深度可分離卷積的區別Fig.2 Difference between ordinary convolution and deep separable convolution

混合所有通道來產生最后的一個輸出，深度卷積將輸入特征映射的每個通道分別卷積，捕獲每個通道的空間特征。逐點卷積集成所有提取的空間特征并學習輸入特征映射的信道相關信息，對獲得的特征圖進行類似于普通卷積的通道融合操作。可以在損失精度不多的情況下降低參數量和計算量。

2 本文模型

2.1 模型介紹

通過上述分析，本文所提出模型的網絡架構如圖3所示，其中包括一個輸入層、三個三維卷積層、兩個深度可分離卷積層、全連接層（包括一個Flatten平滑層、兩個Dense層以及兩個Dropout層），Dropout層主要為了緩解過擬合的問題。卷積層均采用ReLU激活函數進行非線性映射。ReLU 激活函數比傳統的Sigmoid函數和Tanh函數收斂速度更快。ReLU激活函數的形式為：

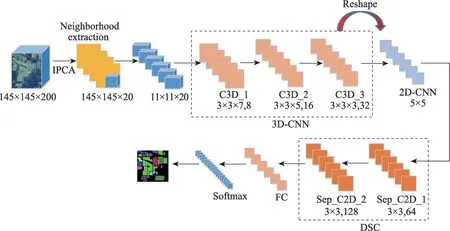
圖3 網絡框架Fig.3 Network framework

最后通過Softmax分類器進行高光譜圖像特征的分類。每個層的輸入輸出維度、參數大小如表1所示。

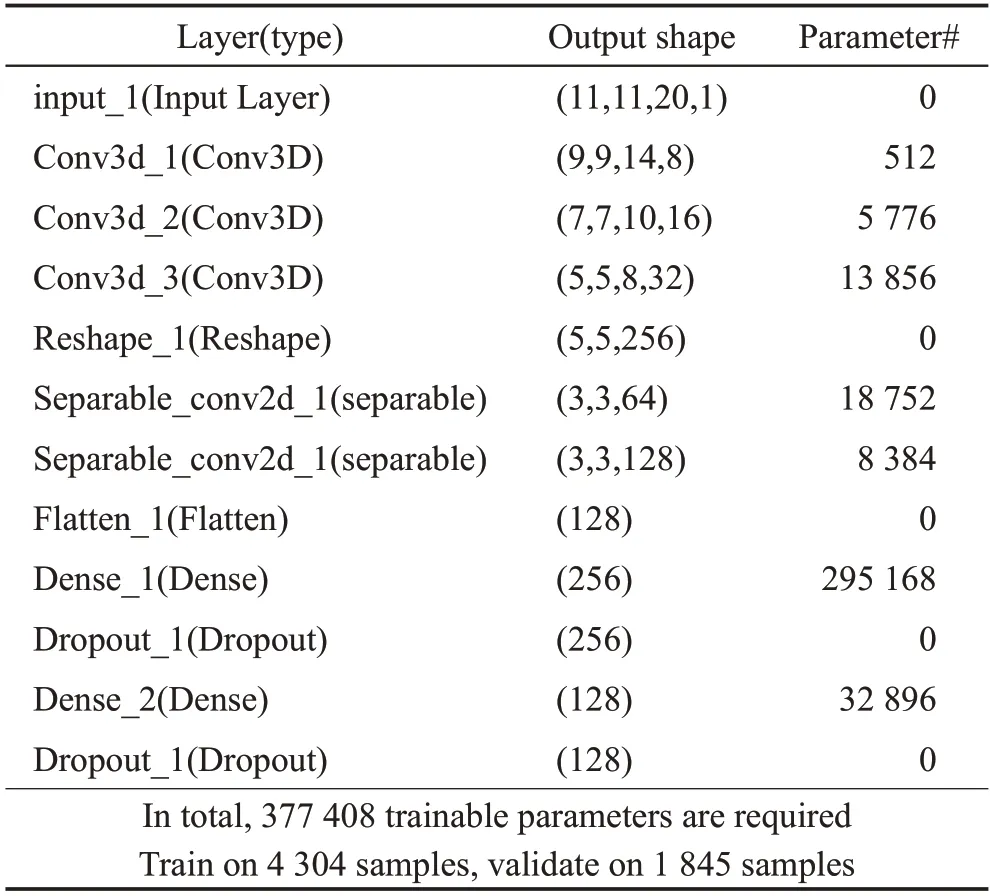
表1 模型在Window Size大小為11×11的IP數據集上的參數Table 1 Parameters of model on IP dataset with Window Size of 11×11

模型中3D-CNN卷積核大小為：3D_conv_layer1=8×3×3×7×1，其中=7；3D_conv_layer2=16×3×3×5×8，其中=5；3D_conv_layer3=32×3×3×3×16，其中=3。最后將三維的輸出特征reshape成二維數據，提取高光譜圖像的空間特征，添加兩個深度可分離卷積層Separable_conv2d_1_layer4=3 × 3 × 64，Separable_conv2d_1_layer5=1×1×128。為了增加空間光譜特征圖的數量，在平化層之前部署了3 個三維卷積層，高光譜圖像的空間信息確定空間維上相鄰像素間的空域特征，并且空域特征可以彌補譜域特征的不足，應用空域特征增加光譜空間的特征，提升高光譜圖像的分類精確度。因此在三維卷積層后增加兩個深度可分離卷積層，在可以減少參數的同時增加空間特征，提取更豐富的空譜特征，確保模型能夠在沒有損失的情況下區分不同波段的空間信息。提出的快速3D-CNN 和DSC 組合模型的總參數（即可調權值）為377 408，比單獨使用快速3D-CNN 的參數少了約一半多。卷積的填充方式選擇零填充，不需要進行批處理歸一化和數據增強。

2.2 IPCA降維與數據預處理

高光譜圖像的像素表現出高類間相似性、高類內變異性，這樣的問題對于任何分類模型都需要密集的處理。為了克服上述問題，需要對數據進行預處理操作。原始的PCA方法會把所有的數據一次性地放入內存中，這在大數據集的情況下有可能會遇到問題，因此提出使用增量主成分分析（IPCA）對數據進行預處理。增量主成分分析能夠避免直接計算協方差矩陣，并且不需要一次性獲得全部圖像數據，它采用增量的學習方式，使用每次新獲得的圖像數據逐步對主元估計值進行迭代更新。訓練集可以分成一個個小批量，一次給IPCA算法輸入一個。

假設輸入向量序列為u′(t)=1，2，…，第n幅圖像輸入時均值為m(n)=，協方差矩陣為：

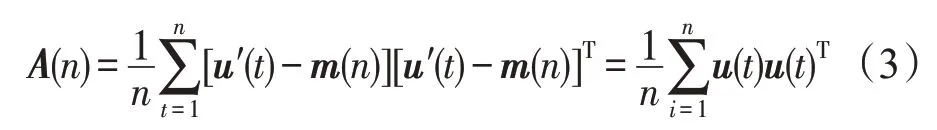
這里u(t)=u′(t)-m(n)，u(n)的第i個特征值和特征向量的計算公式為λixi(n)=A(n)xi[n]，其中xi(n)為第n輸入時待求的第i個特征向量，λi為對應的特征值。IPCA 算法為了加快迭代的速度，整個迭代是對特征值和特征向量的乘積λixi進行的。

IPCA 減少了減少空譜帶間的冗余，獲得比較重要的波段信息，同時保持空間維度的完整性。在圖3中，IPCA將光譜波段從200減小到20，而空間維數保持不變。同時三維立方體分割成小的重疊的三維空間小立方塊，傳遞給模型進行特征提取，并在這些小立方體塊上基于中心像素形成地面標簽。

2.3 3D卷積結合深度可分離的卷積過程

圖4為三維空間光譜特征學習框架。該部分由3個三維卷積層、ReLU 激活函數組成，對高光譜圖像的光譜和空間特征同時提取。網絡的輸入數據大小為11×11×20，第一層卷積核的大小為3×3×8，經過兩層三維卷積操作后，輸出為32 個5×5×8 大小的特征映射。在完成3D卷積操作后，再次進行空間特征提取，利用reshape 進行3D 到2D 變形。為了學習后期二維空間的輸出特征，將三維特征重構為大小為5×5的32個二維特征圖，只需要研究二維空間特征，與三維卷積相比減少了網絡參數和操作成本。

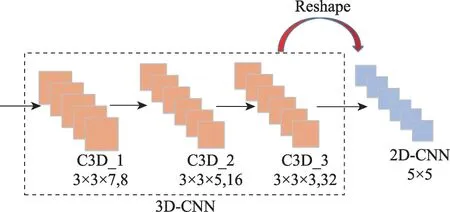
圖4 3D光譜-空間特征學習Fig.4 3D spectral-spatial feature learning

圖5 為基于深度可分卷積的二維空間特征學習。采用深度可分離卷積對輸出的二維特征進行提取，在不引入額外參數的情況下更好地提取空間特征。與傳統的二維卷積不同的是，深度可分卷積在保持信道獨立的情況下進行空間卷積，然后進行深度卷積。通過特征重塑后，網絡輸入數據為256個特征映射，大小為5×5。SeparableConv2D 實現整個深度分離卷積過程，即深度方向的空間卷積和輸出通道混合在一起的逐點卷積。第一步是深度卷積運算，用64 個3×3 大小的卷積核對輸入數據進行卷積運算，得到了64個通道的特征圖，每個卷積核只對輸入層的一個通道進行卷積。第二步是逐像素點卷積運算。用128 個1×1 大小的卷積核在這64 個特征圖上進行卷積運算，將不同通道的信息進行融合。經過1×1的卷積，顯著地減小了尺寸深度。經上層輸出的64個通道，1×1卷積將把這些通道嵌入到單個通道中。1×1 卷積之后，添加Batch Normalization 批量正則化提高模型泛化能力，添加非線性激活函數ReLU，非線性允許網絡學習更復雜的功能。同時每個卷積核與輸入圖像進行卷積，得到一個空間特征映射。深度可分卷積不僅減少了網絡中的參數量和計算量，而且提高了網絡訓練速度，降低了HSI 分類中過擬合的幾率。使用填充來保證輸出特征映射的大小與輸入的大小相同。

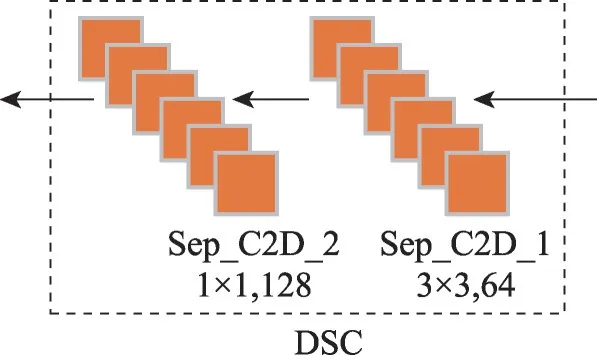
圖5 DSC空間特征學習Fig.5 DSC spatial feature learning

3 實驗及結果

3.1 實驗數據集及實驗描述

3.1.1 高光譜數據集

IP（Indian pines）是由AVIRIS傳感器收集的印第安納州西北部印第安納農林高光譜試驗地的圖像，該圖像由145×145 個像素組成，其中220 個光譜帶，范圍為0.2～0.4 m，空間分辨率很好。將其中20 個噪聲波段移除，該數據集共16類地物。

PU（Pavia University）帕維亞大學數據集在意大利北部的帕維亞收集，使用反射光學系統成像光譜儀（ROSIS）光學傳感器。PU 數據集由610×610 空間和103個光譜波段組成，該數據集包含9類地物。

SA（Salinas scene）數據集由機載可視紅外成像光譜儀（AVIRIS）對美國加利福尼亞州的Salinas 山谷進行成像，空間分辨率為3.7m，其包含512×217個地物像素和224個光譜通道，共有200個光譜通道可用于分類，該數據集包含16類地物。圖6所示是3個數據集的偽彩色圖。

圖6 3個數據集的偽彩色圖Fig.6 Pseudo color maps of 3 datasets

3.1.2 實驗細節描述

在實驗過程中經過不斷的測試調整，將batch size 設為256，epoch 迭代次數設置為50，采用Adam優化器對網絡進行學習訓練，初始學習率設置為0.001（同時設置decay=1E-06 每次參數更新后學習率衰減）進行實驗。采用ReLU 函數作為激活函數，以提高計算效率并加快函數收斂速度。分別隨機選取訓練數據量為60%，測試數據量為40%的IP、PU和SA 數據集進行實驗。為了實驗的公平，對不同的數據集在輸入體積的三維patch中提取了相同的空間維度，例如IP、SA和UP的空間維度均為11×11×20。采用OA、AA 和Kappa 系數和混淆矩陣來評價分類性能，其中OA是用來評價所有樣本的分類正確率，AA是每一類分類的精度，Kappa系數是一種常用來計算分類精度的方法，代表分類與完全隨機的分類產生錯誤減少的比例。混淆矩陣是分別統計分類模型歸錯類、歸對類的觀測值個數，然后把結果放在一個表里展示出來。

3.1.3 實驗環境描述

實驗環境為Intel?Xeon?Silver 4116 CPU @2.10 GHz，內存為128 GB 的PC 機，具體程序由Pycharm2019編寫，在Windows 10系統下基于python3.7的Tensorflow2.0 框架實現。在所有的實驗中，初始測試集/訓練集按40%/60%的比例劃分，將訓練樣本（占總樣本的60%）再按30%/70%的比例劃分為訓練集和驗證集。

3.2 實驗結果及分析

3.2.1 不同降維結果下的分類效果

維度變換是將現有數據降低到更小的維度，盡量保證數據信息的完整性。一般情況下，降維會造成原始數據信息的損失，降維后的數據要盡可能地保留原始數據的信息，本文利用增量主成分分析對數據進行降維，通過給定需要原始數據信息的百分比來確定選擇前75 個主成分，降到20 維，但是如果需要保留更多的原始數據的信息就會造成降維后的維數仍然很多，導致分類效果不明顯。表2基于IP數據集進行實驗分析，在其他的超參數均不變化的情況下，將降維參數NumComponents作為單一變量，統計降維到不同大小的維度時對分類效果的影響。從表中可以看到，在降維到20 的情況下，3 個分類精度指標Kappa、OA、AA均最高，因此在保證其他參數不變的情況下，本文利用IPCA將數據降維到20維是最適合的情況，同時在實驗過程中發現IPCA對數據的預處理速度較快。

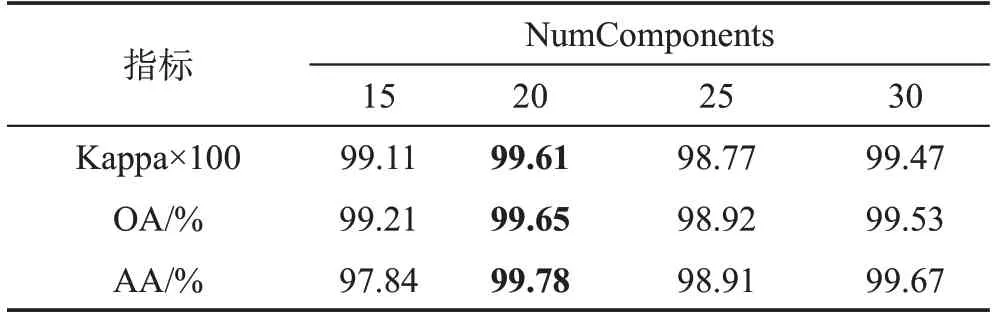
表2 基于IP數據集的不同降維大小下的分類精度Table 2 Classification accuracy of different dimension reduction sizes based on IP dataset

3.2.2 不同空間維度大小對分類的影響

在深度卷積神經網絡中，輸入圖像的尺寸越大，模型卷積參數的數量就越大，計算復雜度也會越高。另外，如果輸入圖像的大小過小，網絡接收的可用字段也會過小，無法獲得良好的分類結果。表3表示不同空間鄰域大小對所提模型性能的影響。設置空間維度大小為9×9×20、11×11×20、13×13×20、17×17×20、23×23×20、25×25×20，在3個數據集上分別通過實驗得到不同窗口的訓練時間以及Kappa、OA、AA的分類精度，訓練時間高度依賴于網速和可用內存以及模型參數量。對OA、AA、Kappa 的精度分析時，可以得出結論，隨著空間維度的逐漸增大，IP 數據集基本呈增長趨勢，PU 數據集在23×23 大小的時候出現下降，但整體還是在增長。SA 數據集的分類精度較穩定，當空間輸入大小達到11×11 時，分類精度開始緩慢變化，11×11的窗口大小在精度和時間上對于3 個數據集IP、PU、SA 是足夠的，而在13×13、17×17、23×23 和25×25 的空間維度大小下幾乎是相同的。通過實驗可以看到在空間維度不斷增大的過程中，模型的各精度指標會顯著增加，但同時參數量增加，計算時間增多。該方法主要是在快速3D-CNN模型的基礎上做的改進，為了比較的公平性，網絡超參數不變，維度大小也選取11×11×20 的情況。通過比較可以看到模型參數量減少，同時各個分類指標的精度也相對較高，訓練時間減少。

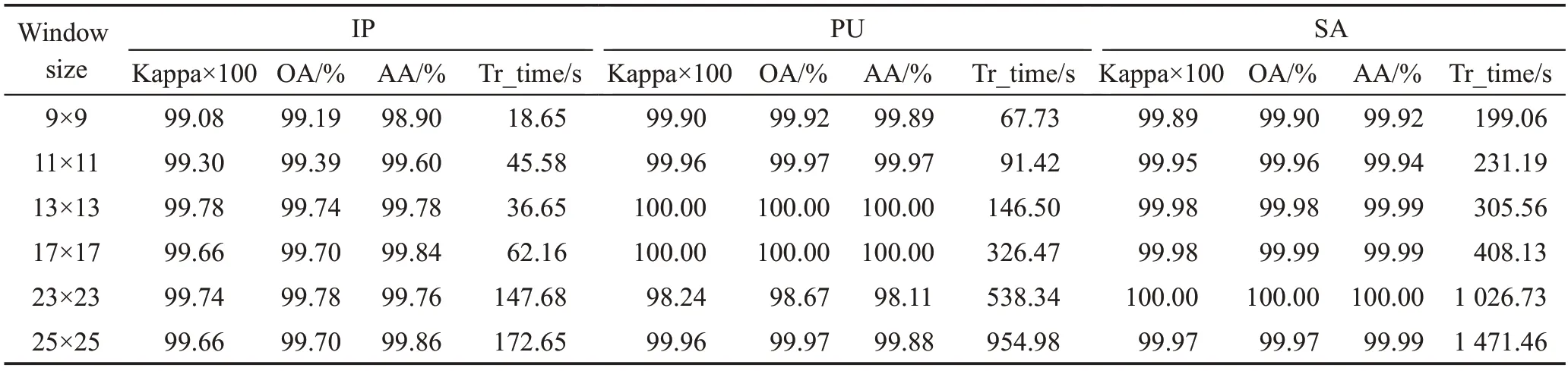
表3 3個數據集上空間維度大小對模型性能的影響Table 3 Impact of spatial window size on proposed model on 3 datasets

3.2.3 分類損失率和準確率

實驗通過訓練和驗證損失率以及準確率來分析網絡模型的穩定性以及擬合度，主要在IP 數據集上進行實驗驗證。圖7 的曲線表示IP 數據集在窗口大小為9×9 的情況下的訓練和驗證集損失率和準確率分類效果，和11×11 大小下的曲線圖圖8 相比較，模型的擬合度不高。文中主要針對11×11 大小的情況進行訓練。從圖8 的曲線可以看到，從（a）圖可以看到模型在epoch達到15左右的時候就開始收斂，訓練集和驗證集的損失率已經接近0。（b）圖epoch達到15左右時也開始收斂，訓練集和驗證集達到將近100%的準確率。從兩個圖中可以看出訓練集和驗證集的曲線基本吻合，不存在較大的震蕩現象，模型的擬合度相當高。通過實驗可以看到所提模型相對穩定，收斂速度非常快，分類精確度較高。

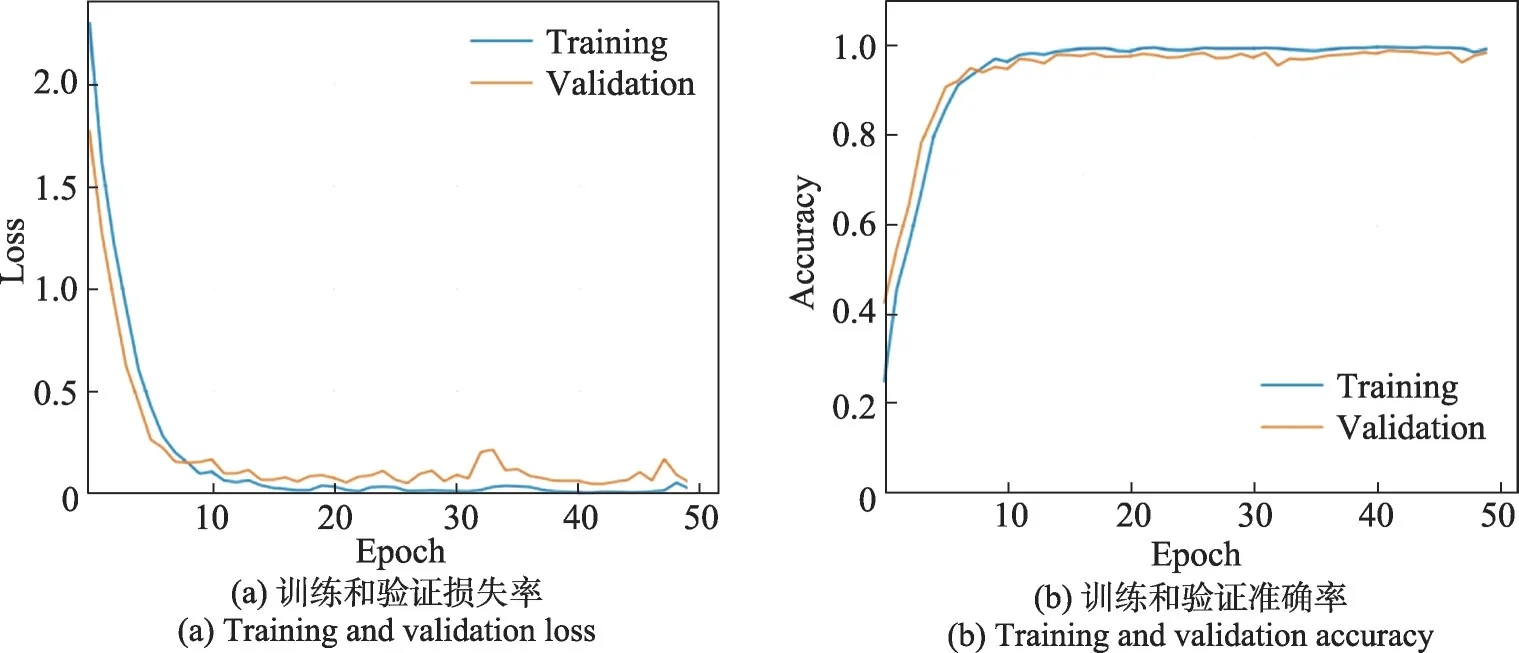
圖7 空間大小為9×9的損失率和準確率Fig.7 Loss and accuracy of space size 9×9

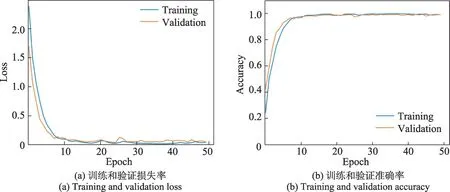
圖8 空間大小為11×11的損失率和準確率Fig.8 Loss and accuracy of space size 11×11

3.2.4 深度可分離卷積的影響

通過比較實驗來測試深度可分卷積的影響。在三維卷積層加入深度可分離卷積，形成比較模型，與快速3D-CNN 的模型進行對比[19]。其他參數設置與Fast-3D-CNN一致。IP、PU和SA數據集的初始測試集/訓練集按40%/60%的比例劃分，將訓練樣本（占總樣本的60%）再按30%/70%的比例劃分為訓練集和驗證集。對不同的數據集提取相同的空間維數11×11×20。圖9～圖11 表示所提模型和Fast-3D-CNN 模型的分類圖對比。從圖中可以看出在其他條件都相同的情況下，加入深度可分離卷積的3D-CNN的分類效果更好。可以看到Fast-3D-CNN 方法最終的分類結果圖中含有大量的斑點，并且存在小區域內錯分的情況。而本文方法的分類結果圖則含有非常少量的斑點，且在同質的小區域內相對平滑，并且好幾類地物幾乎完全正確分類。由此可見，該方法具有較好的分類效果。

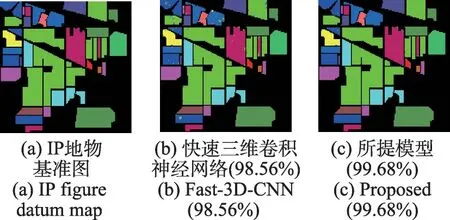
圖9 在IP數據集上兩個模型的分類圖對比Fig.9 Comparison of classification graphs of two models on IP dataset

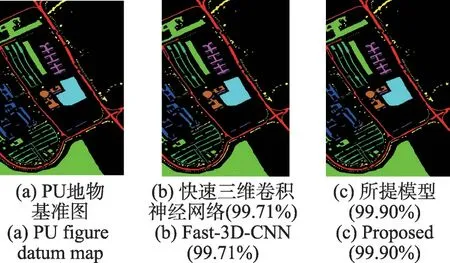
圖10 在PU數據集上兩個模型的分類圖對比Fig.10 Comparison of classification graphs of two models on PU dataset

圖11 在SA數據集上兩個模型的分類圖對比Fig.11 Comparison of classification graphs of two models on SA dataset

3.2.5 不同方法下的實驗性能比較

為了驗證所提網絡模型方法的正確性和有效性，最后將所提卷積模型的實驗結果和傳統的卷積模型2D-CNN[20]、3D-CNN[21]、Multi-scale-3D-CNN[22]和Hybrid SN[23]進行對比。為了保證實驗的公平性，將所有對比網絡中的超參數都設置相同，例如將輸入數據降維到20維，空間維度大小設置為11×11×20，epoch周期為50，batch size為256。同前面實驗一樣，分別從Indian Pines、Salinas scene 和Pavia University三個數據集上隨機選取60%訓練數據、40%測試數據進行驗證，并且重復實驗5 次，最后取這5 次的平均值。表4 為不同方法下的實驗結果。從表中可以看出，提出的方法與其他方法中分類性能最好的方法Hybrid SN 相比較，對于Indian Pines 數據集，其OA高出1.86個百分點，AA高出2.11個百分點，Kappa系數高出2.34。對于Salinas scene 數據集，其OA 高出1.90個百分點，AA高出1.14個百分點，Kappa系數高出2.10。對于Pavia University 數據集，其OA 高出1.53個百分點，AA高出1.90個百分點，Kappa系數高出2.02。可以看出，在快速3D-CNN的基礎上結合深度可分離卷積具有較好的分類效果。圖12 表示PU數據集的混淆矩陣，可以看到PU數據集中大部分地物的分類精度達到100%，如Asphalt、Meadows 和Painted metal sheets 等，只有個別地物被錯分，如將0.1%的Gravel 錯分為Self-Blocking Bricks，表現出較明顯的分類效果。圖13表示不同方法下高光譜圖像分類圖的效果，從效果圖可以看到所提方法的優勢。由此可見，所提及的方法，結合深度可分卷積的快速3D-CNN 模型對高光譜圖像的分類具有較好的分類效果。可以看到錯分的類很少，在混淆矩陣中表現明顯。

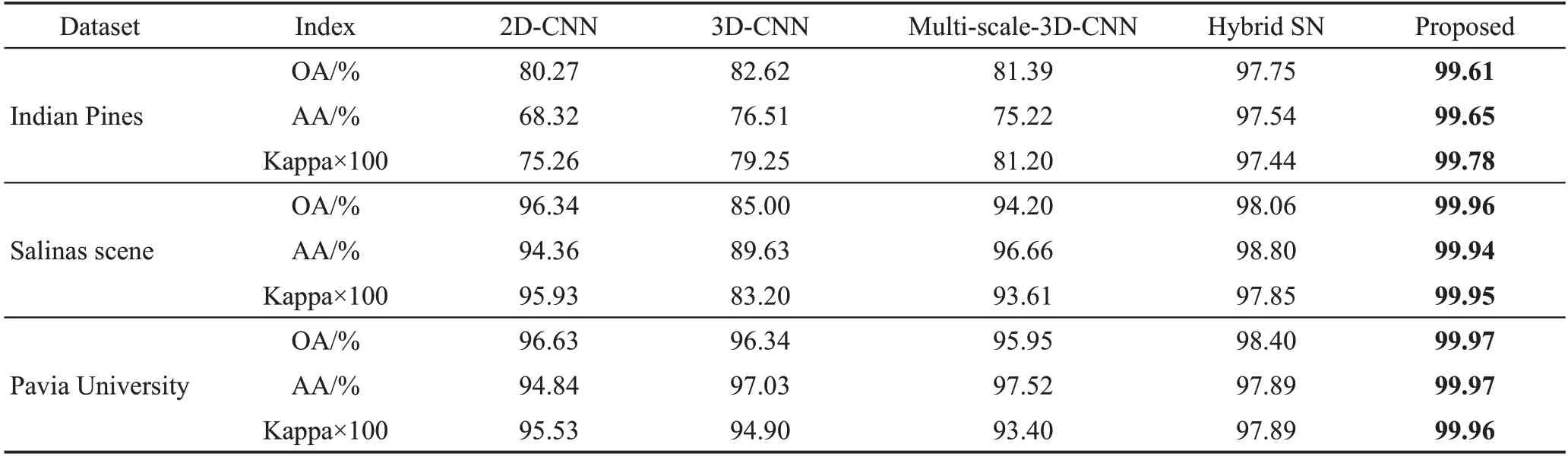
表4 不同方法下的實驗性能對比Table 4 Comparison of experimental performance under different methods

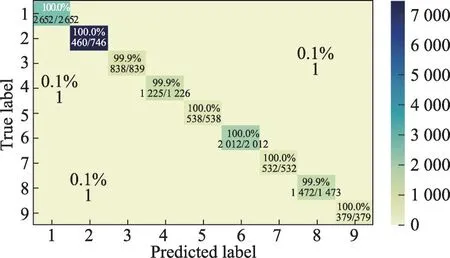
圖12 在PU數據集上的混淆矩陣Fig.12 Confusion matrix on PU dataset

圖13 不同方法在3個數據集上的分類效果Fig.13 Classification effect of different methods on 3 datasets

4 結束語

本文提出的快速3D-CNN 結合深度可分離卷積的高光譜圖像分類方法，首先利用IPCA對高光譜原始圖像進行降維預處理，降低冗余頻譜，減少了圖像波段的數量同時保持空間維度的完整性；利用三維卷積神經網絡同時提取光譜和空間特征，然后引入深度可分離卷積，設計了新的卷積層DSC 層。該層充分發揮了深度可分離卷積對空間特征提取的優勢，能大幅度節省可學習的參數；最后基于兩種卷積方式設計了快速3D-CNN 和深度可分離卷積結合的網絡框架。實驗表明，該方法不僅在有限的標簽樣本下表現出了較好的分類性能，而且同基于標準卷積層的模型相比，大大降低了模型復雜度，減少可學習參數的同時節省了內存空間。

將提出的模型方法和其他傳統的卷積神經網絡的方法相比較，分類性能較好，但是本文中還存在許多不足之處。例如如何設計更加完善的深度卷積網絡模型，解決網絡梯度下滑的問題，這將成為下一步的研究重點。