基于“雙擺模型”的機器人腿部運動模型機理分析
◇咸陽師范學院物理與電子工程學院 徐逸坤 華雪俠 何東山 齊凱強 劉嘉妮
雙擺系統是一個非線性的動力學系統,有著多樣性和復雜性,尤其是其混沌行為。雙擺模型是一種常見的振動系統。碰撞振動作為非線性問題的一種典型情況,廣泛存在于實際工程各個領域中。論文研究以機器人行走過程中雙腿運動特征為基礎,設計構建了基于參數激勵下質量集中的“雙擺模型”結構模型,文章通過對其進行建模、受力分析建立運動方程并研究其運動情況,對其復雜運動進行分析,得到在不同的初始條件下的數據及運動過程的模擬。利用 Tracker 軟件捕捉到的數據,通過控制變量法進行定量分析不同條件下的運動情況。
1 雙擺運動模型理論分析
機器人行走過程中雙腿運動特征可以將其看作由兩個質量分別集中在膝蓋設其質量為的和集中在腳踝質量為兩個質量塊通過輕質桿連接的“雙擺模型”結構系統(如圖1),兩均質桿長度分別為,在O點通過鉸鏈與動點A連接,A沿上下(y軸)周期性往復運動,其運動方程為y=其中為運動幅值,為頻率。這樣的系統是一個非線性的動力學系統,有著多樣性和復雜性,尤其是其混沌行為。
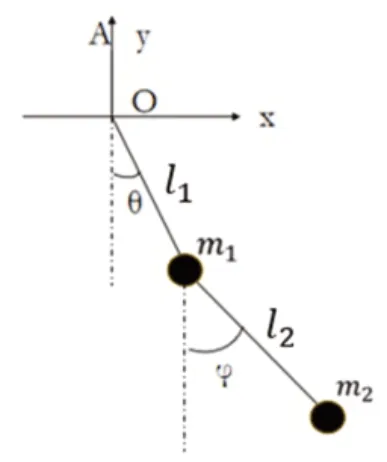
圖1 機器人腿部模型
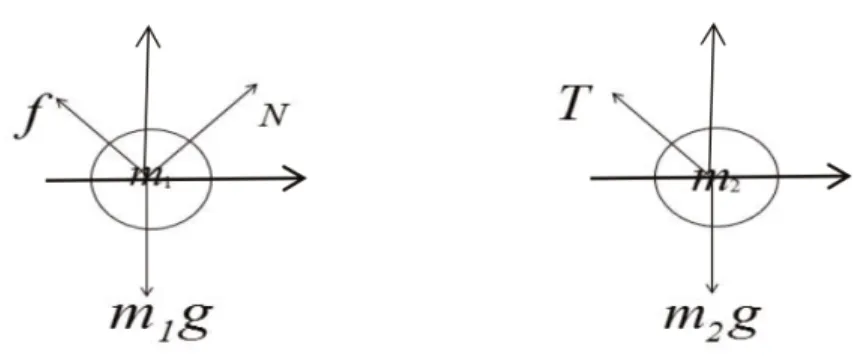
圖2 和 受力分析
由圖1可知:

2 機器人腿部“雙擺運動”模型實驗分析


圖3 圖像

圖4 圖像
圖5 圖像
圖6 圖像
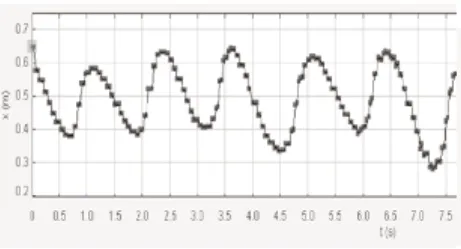
圖7 圖像

圖8 圖像

圖9 圖像

圖10 圖像
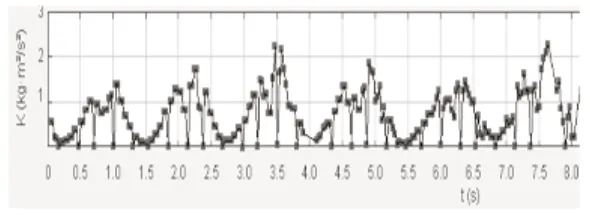
圖11 圖像
拉格朗日方程:

保守力系的拉格朗日方程為:

將公式(7)(8)代入(10),可得機器人腿部模型的參數激振動方程為:
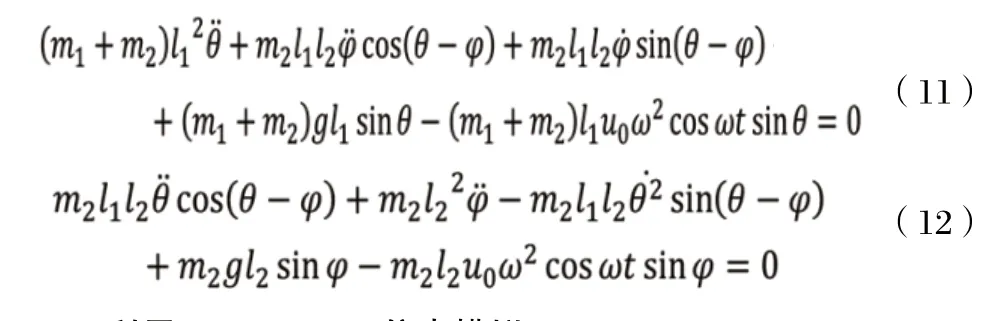
3 利用Mathematica仿真模擬
指出當系統處于較低能級時,系統是近可積的,等值曲線和數值仿真接近,當系統處于較高能級時,系統的運動狀態是混沌的。安宇[4]指出系統在較高能量時,初值的一點變動對系統的運動狀態有很大影響。文獻5指出可以通過Mathematica的NDSolve求解器求解該方程。下面將使用Mathematica來探究初值變化對機器人腿部運動狀態的影響。
3.1 研究和的影響


圖12 計算理論微分方程
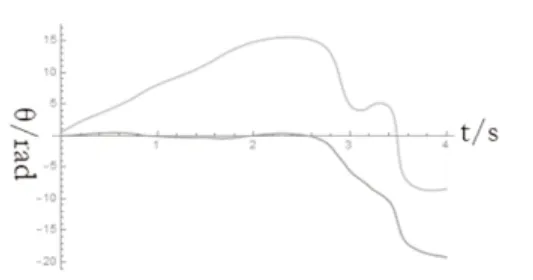
圖13 計算理論微分方程
3.2 研究角速度的影響

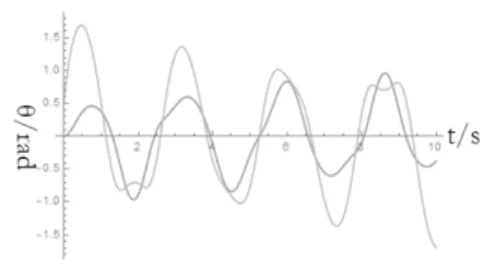
圖14 計算=5rad/s理論微分方程
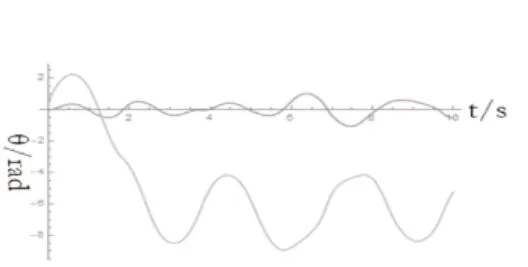
圖15 計算 =6rad/s理論微分方程

圖16 計算=7rad/s理論微分方程
3.3 研究簡諧運動頻率的影響

通過圖17~圖19我們可以發現當ω>2.5rad/s時,機器人腿部模型不能穩定運動,一段時間后,產生混沌現象。
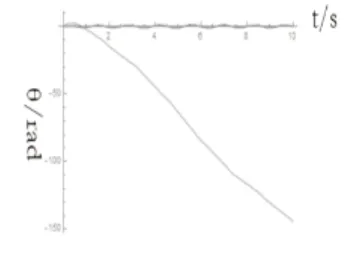
圖17 計算ω>2.2rad/s時

圖18 計算ω>2.3rad/s

圖19 計算ω>2.5rad/s
4 結論
本研究對機器人雙腿進行了的簡化的“雙擺模型”的理論和實驗的分析得出以下結論:①圖像可以看出,在一個周期內系統機械能守恒,所以理論可以使用保守力系拉格朗日算出微分方程。都有周期性變化:在平面里左右擺動;繞周期性運動。②通過仿真與計算得出時經過一段時間后,出現混沌現象。機器人雙腿裝置中膝蓋處質量與足部質量之比需小于時,機器人雙腿裝置中足部角速度需小于等于6rad/s;6rad/s≤≤7rad/s時小球機械能不足,會產生回擺;故不能適用于機器人雙腿裝置;ω≥2.5rad/s時,系統經過一段時間后出現混沌現象。

