地鐵車站結構設計細節優化研究

劉 晨 李 標

地鐵作為城市軌道交通的重要組成內容，具有乘客密集、環境封閉、線路位于地表以下的特征，為保障乘客的出行安全，必須做好地鐵結構設計。結合實際情況，傳統地鐵車站設計以結構自重、水土壓力以及地鐵超載等靜載荷為主要設計指標，但此設計方式中忽略了地震因素對車站結構的影響，以此為施工依據可能會存在安全隱患。

因此，本文在地鐵車站設計分析中引入了結構抗震環節，并且通過有限元仿真分析方法確認不同地鐵車站結構設計細節部分需要重點關注的內容，保障設計的合理性，降低了地鐵車站的安全風險[1]。

1 工程概況

某地鐵車站全長為273 m，地下2層采用狹長箱型結構，標準段外包寬度為20 m。車站采用淺埋暗挖法施工，施工區域內部設置盾構井，主體結構中標準段頂板、底板、中板厚度分別為800 mm、900 mm、400 mm，均采用C35 混凝土；端頭井頂板、底板、中板以及側墻的厚度分別為800 mm、1 000 mm、400 mm、600 mm，均采用C35 混凝土；地下連續墻厚度為800 mm，采用C35 混凝土；單柱尺寸為700 mm×1 200 mm、雙柱尺寸為600 mm×1 100 mm，均采用C40 混凝土。工程地質區域屬于第四紀沖洪積平原區，區域內土層主要由人工填土層、第四紀沉積粉質土、黏性土、砂土以及碎石土組成，地下水位在地面以下20 m。

2 地鐵車站結構仿真模型構建

根據某地鐵車站的實際情況，確定采用SAP2000 有限元分析軟件進行模型構建，模型網格單元尺寸設置為0.5 m。模型中結構部分采用框架單元進行仿真模擬，底板土壓力采用只受壓彈簧模擬。

將某地鐵車站標準段橫斷面具體參數輸入至模型后，運行模型進行仿真計算分析。

3 地鐵車站結構的有限元仿真分析

3.1 標準段橫斷面分析

對某地鐵車站結構關鍵部位彎矩和剪力包絡圖數據統計分析后，確認某地鐵車站標準段彎矩及剪力如表1 和表2所示。

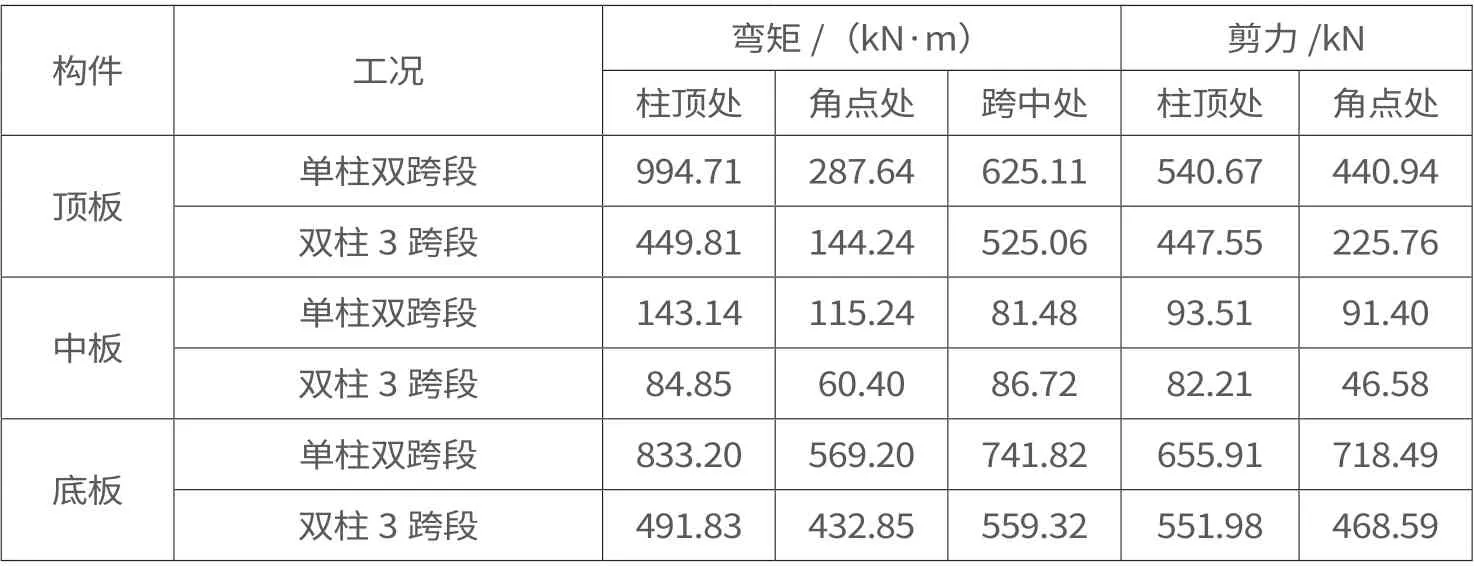
表1 某地鐵車站標準段橫斷面頂板、中板、底板彎矩及剪力統計表

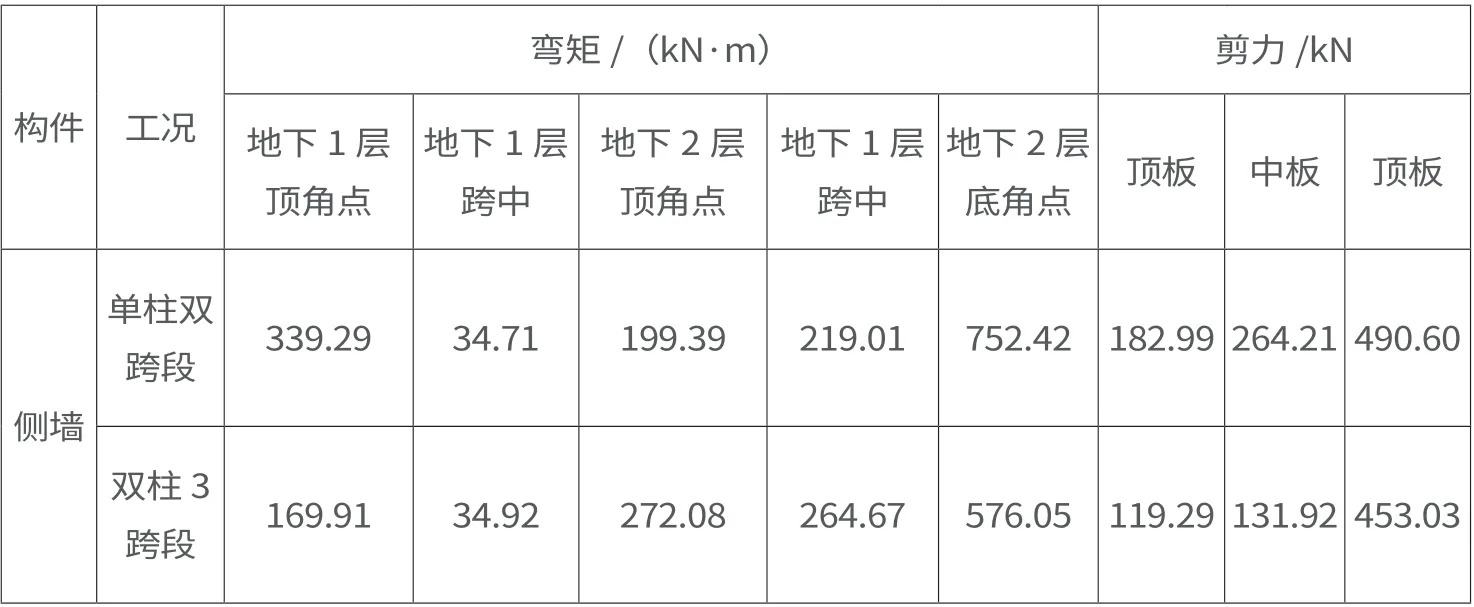
表2 某地鐵車站標準段橫斷面側墻彎矩及剪力統計表

3.2 結構靜力學分析

將以上的參數及某地鐵車站實際數據輸入有限元仿真軟件中，為模型配置基本參數值后實施結構變形以及結構內力仿真分析。據仿真分析結果可知，某地鐵車站單柱雙跨段結構最大彎矩為948.512 6 kN·m，位于單柱雙跨段底板箱型結構角點區域；最大剪力698.642 1 kN，位于單柱雙跨段底板箱型結構角點區域。雙柱3 跨結構仿真分析過程與單柱雙跨段結構仿真分析過程基本一致。通過仿真分析可知，雙柱3 跨段結構的最大彎矩為591.246 kN·m，位于雙柱3 跨段底板箱型結構角點區域和側向底板區域；最大剪力為445.621 6 kN，位于雙柱3 跨段底板箱型結構角點區域。

3.3 地震工況分析

在靜力學仿真分析的基礎上引入地震作用，獲取地震工況下某地鐵車站結構的性能數據。通過仿真分析結果可知，某地鐵車站單柱雙跨段結構的最大彎矩為958.661 3 kN·m，位于單柱雙跨段底板箱型結構角點區域和側向底板區域；最大剪力為731.715 5 kN，位于單柱雙跨段側墻底板區域。

雙柱3 跨段結構的最大彎矩為978.565 1 kN·m，位于雙柱3 跨段底板箱型結構角點區域和側向底板區域；最大剪力為745.217 kN，位于雙柱3 跨段側墻底板區域。

4 地鐵車站結構性能影響因素及設計細節優化方向

4.1 單柱雙跨段

對某地鐵車站靜力學分析和地震工況分析的結果進行歸納，從而形成表3和表4 中的仿真分析結果。

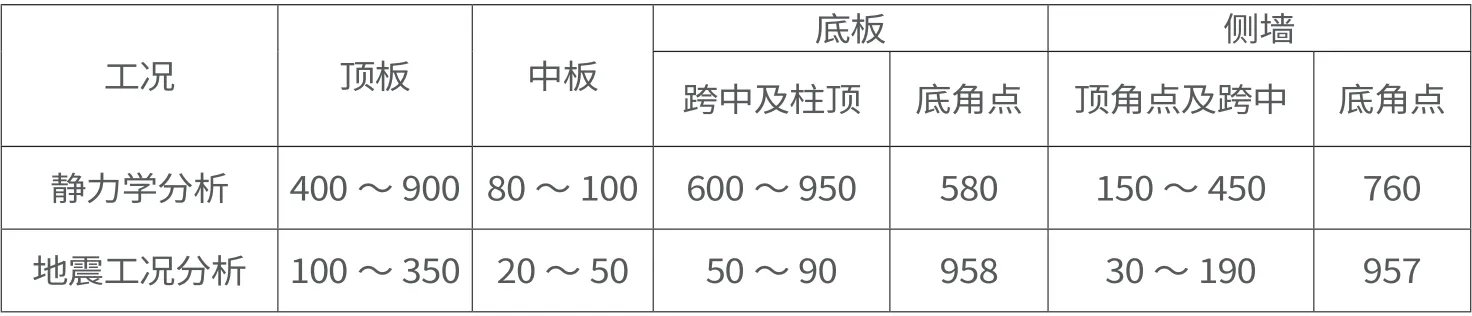
表3 靜力學分析與地震工況分析下彎矩對比（單位：kN·m）

表4 靜力學分析與地震工況分析下剪力對比（單位：kN）

由表3 和表4 可知，對于地鐵車站結構的頂板，靜力學分析和地震工況分析中頂板柱頂、跨中及角點等區域彎矩值為400 ～900 kN·m 和100 ～350 kN·m；靜力學和地震工況分析中柱頂和角點區域的剪力400 ～600 kN 和50 ～300 kN。為保障地鐵車站頂板的綜合安全系數，頂板結構設計中應取較大值，即頂板彎矩及剪力計算應按照靜力學分析過程進行計算和控制[2]。

對于地鐵車站結構的中板，靜力學分析和地震工況分析中，其柱頂、跨中以及角點等區域的彎矩值均分別處于80 ～100 kN·m 和20 ～50 kN·m；靜力學分析和地震工況分析中板中柱頂和角點區域的剪應力分別處于80 ～90 kN和10 ～30 kN。為保障地鐵車站中板的綜合安全系數，中板彎矩及剪力計算應按照靜力學分析過程進行計算和控制。

對于地鐵車站結構的底板，靜力學分析和地震工況分析中，底板柱頂和跨中以及角點等區域彎的矩值分別處于600 ～950 kN·m 和580 kN·m、50 ～90 kN·m 和958 kN·m；靜力學分析和地震工況分析中底板柱頂和角點區域的剪應力分別處于650 ～700 kN 和50 ～450 kN。為保障地鐵車站底板的綜合安全系數，底板彎矩及剪力計算應按照靜力學分析過程進行計算和控制。

對于地鐵車站結構的側墻，靜力學分析和地震工況分析中，側墻頂點及跨中、底角點彎矩分別處于150 ～450 kN·m和760 kN·m、30 ～190 kN·m 和957 kN·m；靜力學分析和地震工況分析中側墻頂板、中板及底板處的剪應力分 別 為190 kN 和250 kN、490 kN 和130 kN、480 kN 和730 kN。為保障某地鐵車站側墻的安全系數，綜合分析后確認側墻頂角點及跨中彎矩應采用靜力學分析，底角點彎矩應采用地震工況分析；中板處剪應力應采用靜力學分析，頂板和底板處剪力應采用地震工況分析[3]。

4.2 雙柱3 跨段

對某地鐵車站靜力學分析和地震工況分析的結果進行歸納，形成表5 和表6中的仿真分析結果。

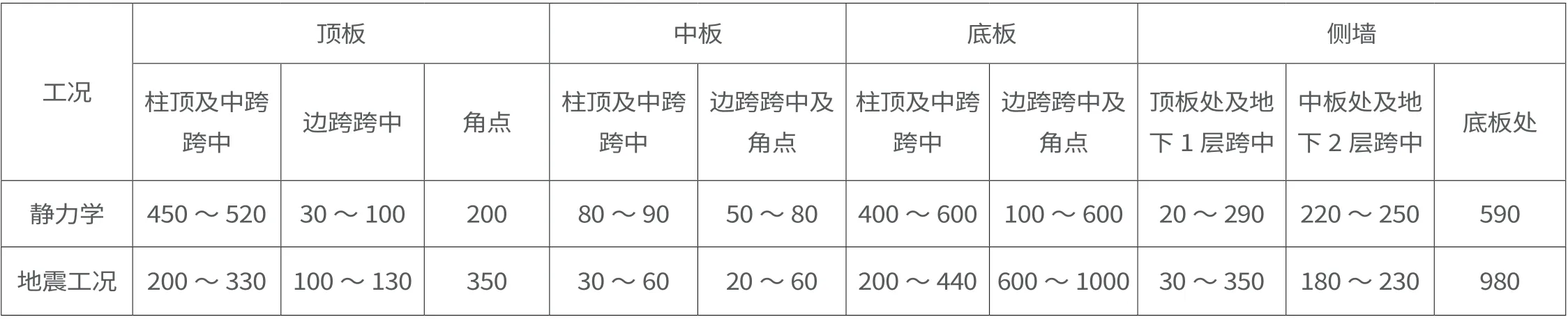
表5 靜力學分析與地震工況分析下彎矩對比（單位：kN·m）

表6 靜力學分析與地震工況分析下剪力對比（單位：kN）

對于地鐵車站結構的頂板，相較于靜力學分析，地震工況分析下角點和邊跨跨中彎矩更大，而柱頂及中跨跨中彎矩較小；同時，相較于靜力學分析，地震工況分析下頂板柱頂及角點剪力較小。為保障地鐵車站頂板的綜合安全系數，頂板結構設計中應取較大值。因此，地鐵車站結構頂板柱頂、中跨跨中處彎矩計算應優先選擇靜力學控制；角點、邊跨跨中彎矩應優先選用地震工況控制；頂板剪力計算應優先采用靜力學控制。

對于地鐵車站結構的中板，相較于靜力學分析，地震工況分析下柱頂及中跨跨中、邊跨跨中及角點彎矩均較小；同時，相較于靜力學分析，地震工況分析下中板柱頂及角點剪力相對較小。因此，地鐵車站結構中板彎矩及剪力計算均應優先采用靜力學控制[4]。

對于地鐵車站結構的底板，相較于靜力學分析，地震工況分析下柱頂及中跨跨中彎矩相對較小，而邊跨跨中及角點彎矩相對較大；相較于靜力學分析，地震工況分析下柱頂和角點處剪力均相對較大。因此，地鐵車站結構底板柱頂及中跨跨中彎矩計算應優先選用靜力學控制，而跨中及角點彎矩計算應優先選用地震工況控制；底板剪力應優先選用地震工況控制[5]。對于地鐵車站結構的側墻，相較于靜力學分析，地震工況分析下頂板處及地下1 層跨中和底板處彎矩相對較大，而中板處及地下2 層跨中彎矩相對較小；同時，相較于靜力學分析，地震工況分析下側墻頂板處和底板處剪力相對較大，而中板處剪力相對較小。因此，地鐵車站結構側墻彎矩計算中頂板處及地下1 層跨中和底板處彎矩計算應優先選用地震工況控制，中板處及地下2層跨中彎矩計算應優先選用靜力學控制；側墻剪力計算中頂板處和底板處剪力計算應優先選用地震工況控制，中板處剪力計算應優先選用靜力學控制[6]。

5 結語

本文以某地鐵車站為研究對象，結合地鐵車站的實際數據，通過仿真分析方法獲取某地鐵車站結構設計細節優化方向及控制要點。根據文中分析結果可知，某地鐵車站單柱雙跨結構斷面區域內的底板角點和側墻底板角點及跨中抗彎性能、側墻頂、底角點抗剪性能均需要根據地震工況控制進行相應加強；雙柱3 跨結構斷面中頂板、中板以及底板角點和跨中抗彎性能、地下1 層側墻跨中和地下2 層側墻底角點抗彎性能、側墻頂角點和底角點抗剪性能均需要根據地震工況控制實施相應加強。