具有附加彈性支承的圓形薄板結構振動分析

王 棟，朱書月

（1.西北工業(yè)大學 航空學院，西安 710072；2.中航西安飛機工業(yè)集團股份有限公司，西安 710089）

圓形薄板是典型的工程結構形式，在實際工程有廣泛的應用。近年來，有關圓板結構振動特性及響應的研究已有豐富的成果，采用解析或數(shù)值方法能有效地求解圓板結構的振動問題[1－3]。這些方法的基本思路都是基于結構的邊界條件，修改相應的位移試函數(shù)或插值函數(shù)來獲得結構的振動特性。Liu和Lee[1]采用有限元法分析了三維圓板結構(考慮厚度)的振動頻率與振型。Gupta等[2]采用微分-積分方法分析了非均質變厚度圓板結構的自由振動問題。Zhou 等[3]利用對偶法求解固有頻率，從而求得了不同尺寸的圓形、環(huán)形和扇形薄板的振動特性，并與有限元數(shù)值結果進行比較，從而驗證了該方法的準確性。石先杰等[4]采用譜幾何法建立彈性邊界條件下圓板結構橫向自由振動分析模型，并將求解結果與有限元法計算、實驗結果進行對比，驗證了譜幾何法的精確性和有效性。陳美霞等[5]研究了彈性邊界條件下圓板的流-固耦合振動特性，將圓板位移展開為級數(shù)形式，并采用速度勢函數(shù)描述流體運動。王忠民等[6]基于微分求積法分析了旋轉圓板的橫向振動和穩(wěn)定性問題，對于變系數(shù)的圓板的軸對稱運動微分方程，采用微分求積法離散方程和邊界條件，分析了周邊固支、簡支和自由3 種約束條件下旋轉圓板的前幾階復頻率值。

對于一般的結構，支承不僅能起到固定結構的作用，還能改變結構的剛度分布及其動力學性能，有效控制結構的振動響應。對于具有附加支承的薄板結構，其相應的動力性能分析以及附加支承的優(yōu)化設計研究也取得到了一定的成果。Wang[7]分析了環(huán)形支承圓板結構的振動模態(tài)，研究發(fā)現(xiàn)當支承沿徑向發(fā)生移動時，圓板結構的模態(tài)會發(fā)生轉換。Zur[8]利用擬格林函數(shù)求解了具有固支、自由和簡支邊界的功能梯度圓板振動頻率問題。綜合研究了邊界約束條件、體積分數(shù)指數(shù)、環(huán)支承位置和剛度對圓板固有頻率的影響。Kumar[9]總結了瑞利-里茲(Rayleigh–Ritz)法在結構靜、動力分析與計算中的廣泛應用。Wang 等[10]采用瑞利-里茲法對矩形板附加彈性支承的位置進行了優(yōu)化設計，計算了使薄板的基頻達到原系統(tǒng)的第2 階固有頻率所需的最小支承剛度值。通過求解特征方程的最小正值解，獲得了板的附加支承在最優(yōu)位置的最小剛度值。近期Wang 和Friswell[11]分析了附加支承附帶質量對彈性支承最優(yōu)設計的影響。然而對于圓形薄板結構附加彈性支承問題，相關的研究成果卻比較少。附加支承對圓形薄板結構振動性能的影響也有待進一步深入研究和分析。

本文采用瑞利-里茲法分析計算圓形薄板結構附加彈性鉸(點)支承時的振動特性，保證支承位置能在結構內能連續(xù)移動，不受有限元法網(wǎng)格劃分的限制。采用正交梁多項式作為圓板的徑向位移試函數(shù)，用完整的傅里葉級數(shù)作為圓板周向位移試函數(shù)，確保圓板結構的對稱與反對稱模態(tài)能完備地獲取。通過與有限元計算結果的對比，驗證了本文方法的正確性和有效性。隨后分析了附加支承的數(shù)量、剛度和位置對圓板固有頻率的影響，探討了圓板結構第一階固有頻率與附加支承分布對稱性的變化情況。

1 圓板彎曲振動基本方程

如圖1 所示，假設一個厚度均勻的彈性圓環(huán)形薄板結構作橫向自由振動，板內有一個彈性鉸支承與基礎相連。圓環(huán)形薄板的外半徑是a，內半徑是b，內外半徑之比為c=b/a，厚度為h。在極坐標r?θ平面內，支承位置為p(rs，θs)。根據(jù)克希霍夫薄板理論(Kirchhoff hypothesis)，在極坐標系下圓環(huán)形薄板的自由振動特征方程為[3]：

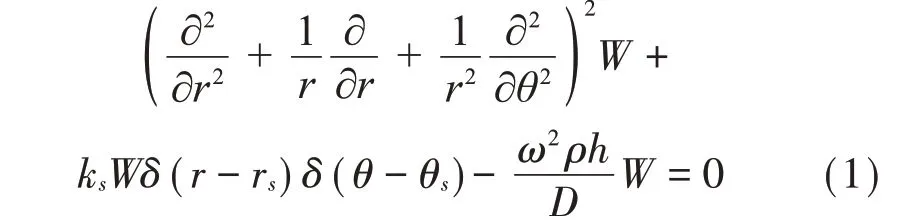
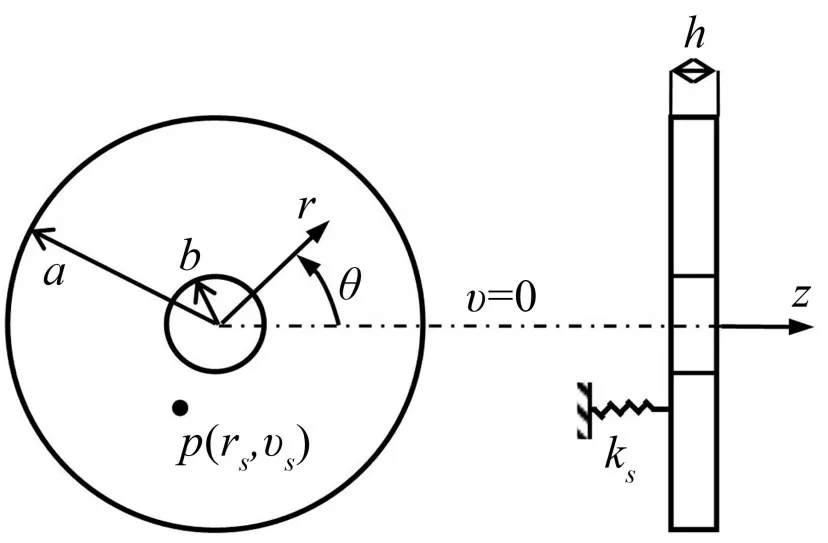
圖1 圓環(huán)形薄板結構附加一個彈性支承

式中：ω表示結構的固有振動頻率，D=D=是薄板的彎曲剛度，E是材料的彈性模量，μ是泊松比，ρ是材料體積密度。ks是附加支承的剛度系數(shù)，δ(?)是Dirac Delta函數(shù)。為了避免分析計算過程中出現(xiàn)分母為零的情況，本文將圓形板近似成內半徑b極小的環(huán)形薄板。

根據(jù)瑞利-里茲法，本文將圓(環(huán))形薄板的橫向位移函數(shù)W(r,θ)近似表達為：

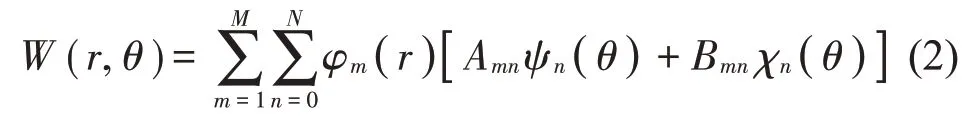
式中：φm(r)、ψn(θ)和χn(θ)分別表示圓板沿徑向與周向的位移試函數(shù)，并且φm(r)至少要滿足圓環(huán)板內外邊界幾何約束條件。M和N為沿著徑向與周向位移試函數(shù)所取的項數(shù)。未知系數(shù)Amn與Bmn將由振動特征方程確定。對于彈性圓形薄板，根據(jù)其振動模態(tài)對稱性的特點，本文在圓板兩個方向上分別取不同形式的位移試函數(shù)。

2 位移試函數(shù)選取

2.1 徑向位移試函數(shù)

采用正交梁特征多項式作為圓板沿徑向的位移試函數(shù)[12]。根據(jù)圓板的內外邊界約束情況，先獲得等效的梁的邊界約束條件，從而確定初始的位移試函數(shù)φ1(ξ)。再根據(jù)Gram-Schmidt遞歸過程構造其他各項位移試函數(shù)：

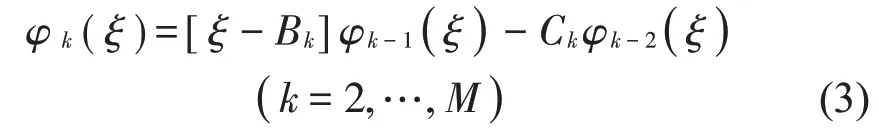
其中各項試函數(shù)應滿足正交性條件：

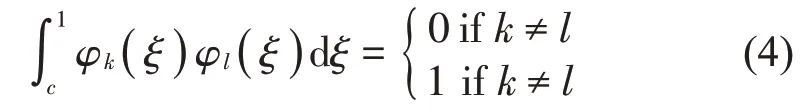
根據(jù)以上條件，試函數(shù)構造式中的系數(shù)Bk和Ck分別為：

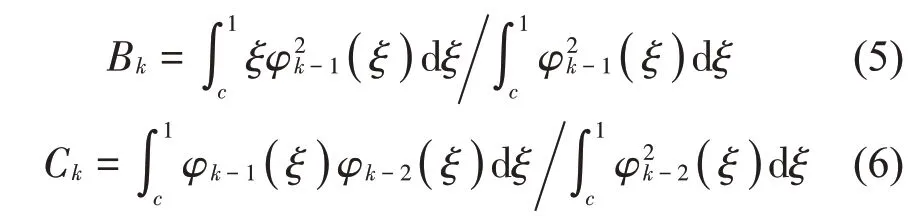
定義φ0(ξ)為0。而初始位移試函數(shù)φ1(ξ)按如下多項式分別構造：

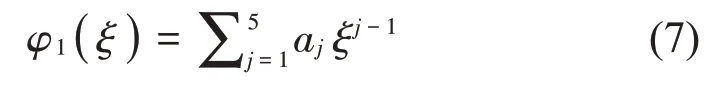
其中的系數(shù)aj(j=1，…，5)按照圓環(huán)徑向內、外邊界約束，根據(jù)等效梁的邊界條件確定[12]。各典型約束邊界對應的系數(shù)如表1所示。

表1 邊界約束條件與初始位移函數(shù)中的系數(shù)

對于圓板結構，由于采用的是內半徑極小的圓環(huán)板來近似圓形薄板，因此其位移試函數(shù)的內邊界全部按自由狀態(tài)選取，允許圓板的圓心自由變形。實際只需考慮圓形薄板外邊界的約束狀況即可。

2.2 周向位移試函數(shù)

由于圓板沿周向位移函數(shù)需要滿足對稱性的條件，因此在式(2)中采用完整的傅里葉級數(shù)作為位移容許函數(shù)：

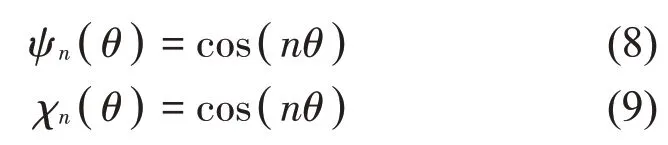
同時引入傅里葉級數(shù)的正弦和余弦函數(shù)，希望能很好地模擬彈性圓板的振動特性，特別是要準確獲得沿圓周方向的正、反對稱模態(tài)，以及重合的結構固有頻率信息。

此外，所取的位移試函數(shù)項數(shù)也影響到本文所用方法計算結果的準確性，一般要根據(jù)結構振動特點設置合理的項數(shù)。經(jīng)過多次試算和收斂性分析，本文在各坐標軸方向上分別選取了7 項，所得頻率計算結果基本達到了穩(wěn)定。

3 頻率特征方程的建立

為了抑制薄板的振動水平，在保持原結構不變的情形下，可以采取附加支承的方式改變板的固有頻率和振型[10]。假設鉸支承是無質量的，用一個橫向線彈簧表示，如圖1所示。在極坐標系統(tǒng)下，附加一個彈性鉸支承時，圓板的最大彈性勢能可表示成[3]：

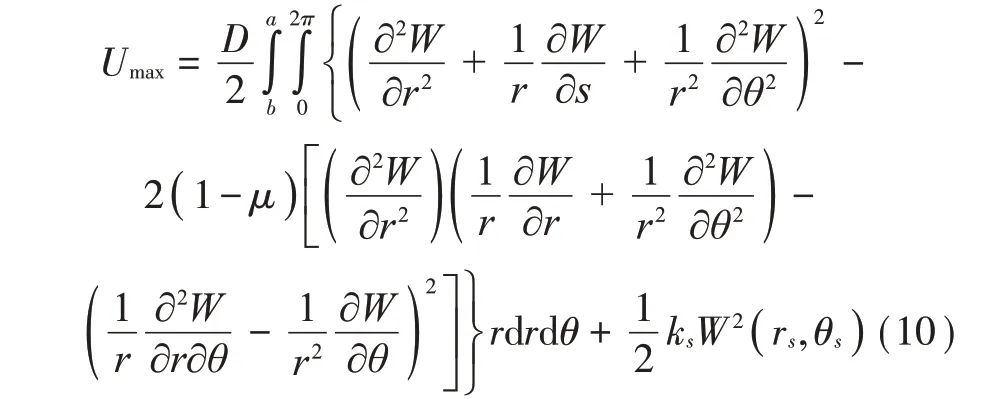
其最大的動能表達式為：

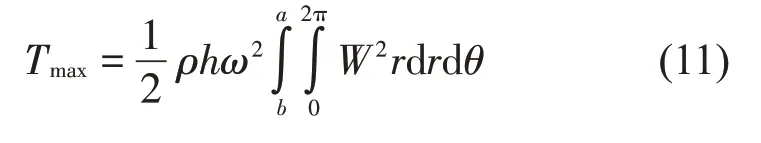
根據(jù)瑞利-里茲方法，彈性圓板結構橫向自由振動的拉格朗日函數(shù)L=Umax-Tmax對系數(shù)Amn與Bmn的變化應取極值[12]：

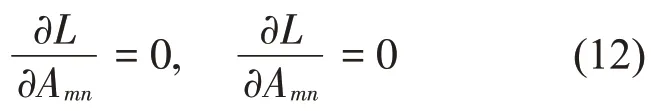
進行無量綱化處理后即得到以下頻率特征方程：

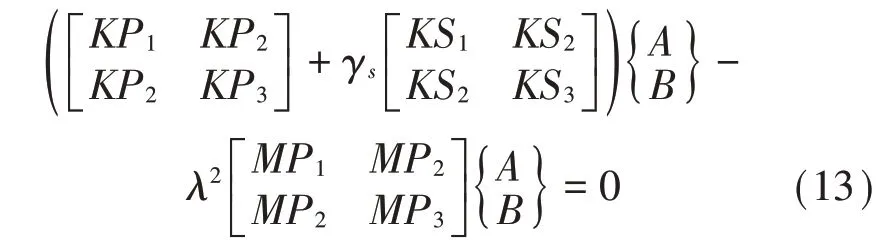
式中：無量綱化的彈性支承剛度系數(shù)γs為：

固有頻率參數(shù)：

支承等效剛度矩陣中各項分別由式(16)至式(18)計算：

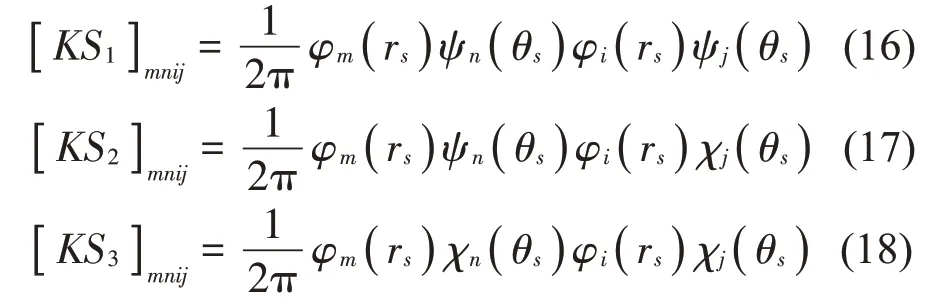
圓板結構剛度和質量矩陣中各項計算見本文附錄。

根據(jù)以上推導結果，當附加多個鉸支承時，只需要在圓板結構剛度矩陣的基礎上疊加各支承的等效剛度矩陣，構成整個系統(tǒng)的剛度矩陣即可。通過求解頻率特征方程式(13)，可得到具有支承情況下系統(tǒng)的固有頻率與振型。若將支撐剛度系數(shù)值設為零γs=0，即可得到無附加支承時圓板結構的振動特性。此外，在給定系統(tǒng)的固有頻率和支撐位置的情形下，還可以求解所需的附加支撐剛度[10－11]。

4 數(shù)值算例分析

為了驗證本文提出的位移試函數(shù)選取結果的可行性和完備性，以及頻率特征方程式(13)推導的正確性，下面對幾個典型數(shù)值算例進行分析，并與有限元Ansys計算結果進行對比。采用有限元網(wǎng)格沿圓板徑向均勻劃分40個單元，沿周向均勻劃分36個單元，共有144 個四節(jié)點板單元。假設彈性圓形薄板的厚度h=0.01 m，外半徑a=1 m，內外半徑之比c=0.000 1。材料的彈性模量E=210 GPa，泊松比μ=0.33，密度ρ=7 850 kg/m3。

4.1 附加支承對圓板固有頻率的影響

考慮幾種典型邊界約束條件，計算附加支承在不同位置、不同剛度以及不同數(shù)量情形下圓形薄板結構的固有頻率。

(1)圓心處附加1個彈性鉸支承，支承剛度系數(shù)γs=2。各經(jīng)典邊界條件的計算結果如表2所示。

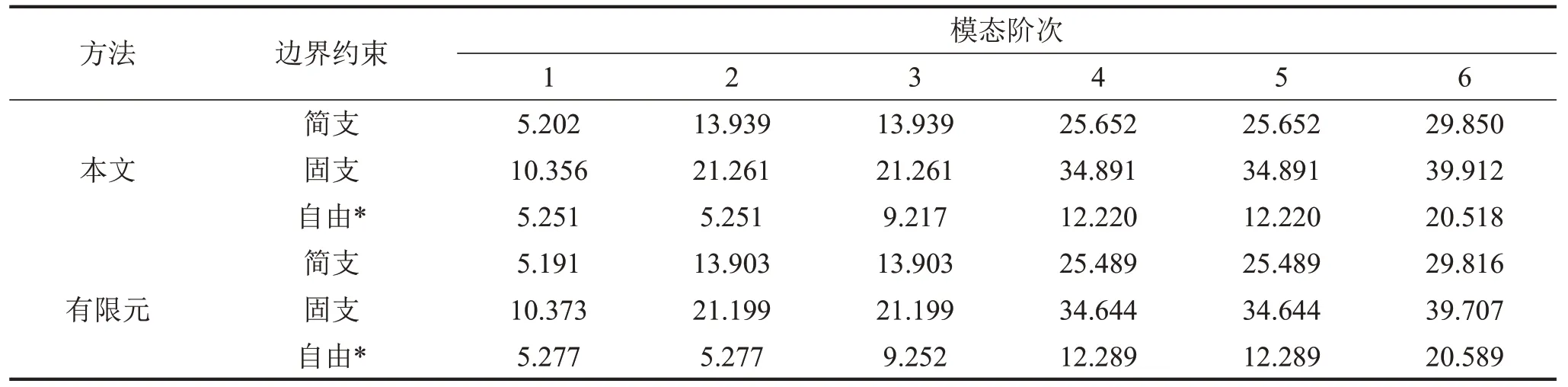
表2 圓心處附加一個彈性支承時圓板的固有頻率λi計算結果

(2)邊界條件為簡支，在rs=0.5 m處沿周向分別均勻分布3 個(相差2π/3)或4 個(相差π/2)等剛度的彈性鉸支承，如圖2所示。支承剛度γs=2，計算結果如表3所示。

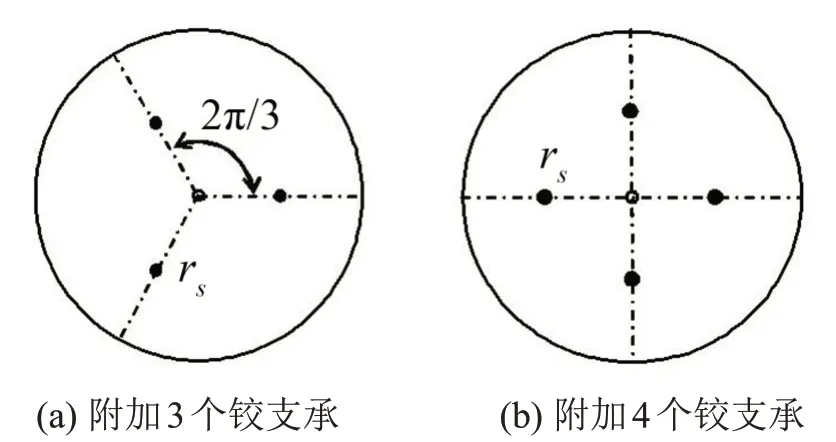
圖2 圓板結構均勻附加3個或4個鉸支承

(3)邊界條件為簡支時，在rs=0.4 m處沿周向均布4 個等剛度的彈性鉸支承，無量綱支承剛度分別為γs=2和γs=5。計算結果如表4所示。

分析比較以上3 種情形的頻率計算結果，可以得出以下結論：

(1)本文提出的位移試函數(shù)能夠很好地模擬圓板的橫向振動狀況。圓板固有頻率的重合情況(對應于正、反對稱模態(tài))都能被完整地呈現(xiàn)出來。

(2)當支承位置不在結構振型的節(jié)點或節(jié)線上時，附加支承可以使結構的固有頻率升高。附加支承的數(shù)量越多，圓板結構的固有頻率升高也越多，如表3 中結果所示。這是由于支承的數(shù)量越多，振動系統(tǒng)總體剛度越大，結構的固有頻率自然會越高。

(3) 支承剛度越大，彈性圓板的固有頻率也越高，如表4 中結果所示。但若將附件支承置于某一階振型的節(jié)線上，固有頻率不會因附加支承剛度的存在而改變，如表4中的第4階固有頻率。

(4)附加支承的位置對圓板結構的固有頻率也會有影響。從表3 和表4 中附加4 個支承的結果可知，在支承剛度相同的情況下(γs=2)，支承位置分別在rs=0.4 和0.5 m 處，圓板結構的固有頻率(特別是第1階固有頻率)升高程度并不相同。

表3 附加不同數(shù)量彈性支承時簡支圓板固有頻率λi計算結果

表4 附加4個彈性支承時簡支圓板固有頻率λi計算結果

4.2 支承位置分布對稱性對圓板固有頻率的影響

以下以3個附加支承為例，分別探討其中1個支承的徑向位置坐標rs以及周向位置坐標θs改變時，自由邊界圓板結構第1階固有頻率變化情況。

(1)沿周向均勻分布3個等剛度的彈性支承，支承剛度γs=2。其中2 個支承固定在rs=0.5 m 處，另1個支承可沿著徑向移動，如圖3所示。

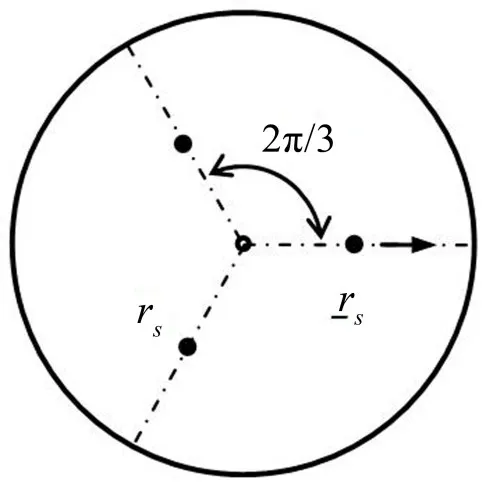
圖3 自由圓板附加3個支承(其中1個支承的徑向位置坐標可變)

隨著其中1個支承的移動，3個附加支承的分布不再具有對稱性。圖4 示出了圓板的第1 階固有頻率與其中1個支承位置徑向坐標變化的關系曲線。隨著位置坐標從0逐漸增大，圓板結構的固有頻率持續(xù)增大，當這個支承位于=0.5 m 處時，此時3 個支承的位置剛好是對稱分布，結構的第1 階固有頻率上升到最大值(λ1=0.963 1)。此后隨著支承的繼續(xù)移動，第1階固有頻率不再改變。

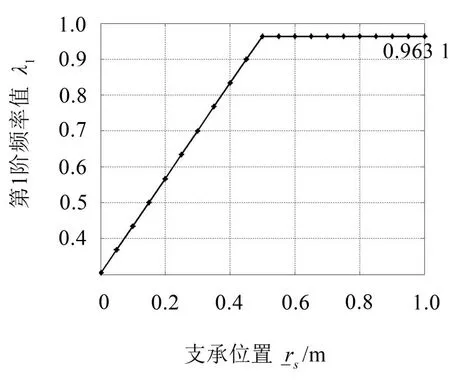
圖4 附加3個等剛度的支承時，其中1個支承的徑向位置坐標與結構固有頻率關系曲線

出現(xiàn)這種情況的原因是，當<0.5 m 時，第1 階振型的節(jié)線不會通過該移動支承所在點，如圖5(a)所示，因此移動該支承將影響圓板的第1 階固有頻率；當≥0.5 m 時，第1 階振型的節(jié)線剛好通過該支承位置，移動該支承并不影響圓板結構第1 階固有頻率，如圖5(b)圖所示。

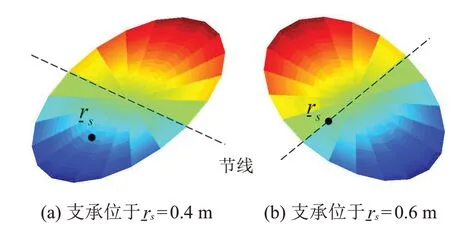
圖5 支承在不同位置時自由圓板結構第1階振型

(2)在rs=0.5 m 處，沿周向分別布置3 個等剛度的支承γs=2。其中2 個支承固定在θ=±2π/3 處，另1個支承在θ=0 軸線附近沿周向移動，即該支承周向坐標θs可變，如圖6所示。

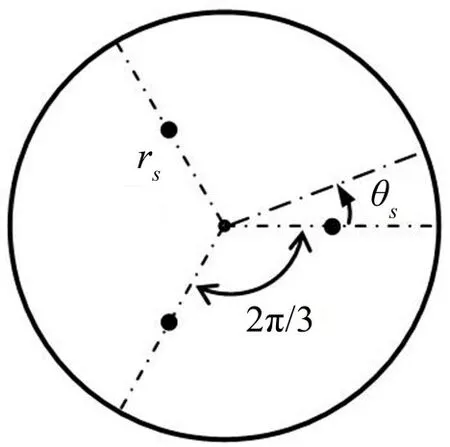
圖6 自由圓形薄板附加3個支承(其中1個支承的周向坐標θs可變)

圖7 示出了圓板的第1 階固有頻率隨其中1 個支承周向位置坐標θs變化的曲線。

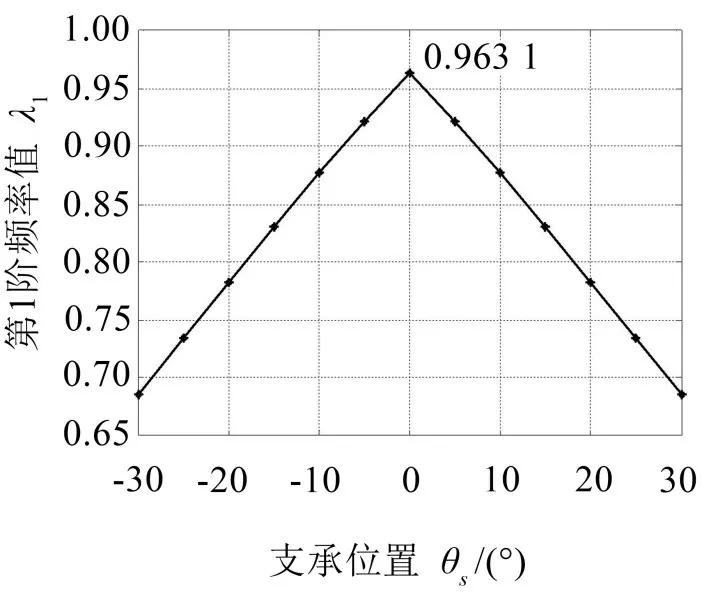
圖7 附加3個等剛度的支承時，其中1個支承的周向位置坐標與結構固有頻率關系曲線

可見，支承周向位置偏移對圓板結構第1 階固有頻率影響較大。只有當這個支承位于θs=0 的位置，即3個附加支承沿周向對稱分布時，圓板結構的第1 階固有頻率才達到最大值(λ1=0.963 1)。否則，圓板結構的第1階固有頻率會顯著下降。

由以上計算結果可知：附加支承沿徑向和周向分布狀況對圓形薄板結構第1階固有頻率有很大的影響。只有當附加支承的分布具有對稱性時，圓板結構的第1階固有頻率值才能達到最大值。若由于某種客觀原因支承無法對稱分布時，圓板結構的第1階固有頻率有可能會顯著下降。因此應盡量保持支承靠近對稱點，以使附加支承能充分發(fā)揮作用。

5 結語

本文采用瑞利-里茲法計算了圓形薄板附加支承時，不同約束邊界條件下結構的固有頻率。用正交梁多項式作為圓板徑向位移試函數(shù)，用傅里葉級數(shù)作為圓板周向試函數(shù)，保證計算結果的完備性和正確性，準確模擬圓板結構固有頻率的重合現(xiàn)象。

計算結果表明：

(1)附加支承的剛度、數(shù)量和位置與結構的力學性能緊密相關。改變附加支承的設計對結構的振動特性會有很大的影響。

(2) 在支承剛度、數(shù)量等其他條件不變的情況下，對稱分布的支承布局可以更有效地提高結構的固有頻率。