EEMD-四線性平行因子的機械多故障欠定盲分離方法
朱亞靜,李澤東,李志農(nóng) ,谷士鵬,馬亞平
(1.南昌航空大學 無損檢測教育部重點實驗室,南昌 330063;2.中國飛行試驗研究院,西安 710089)
平行因子(Parallel Factor,PARAFAC)在寬松條件下具有分解唯一性的優(yōu)勢,在機械故障診斷中獲得了成功應用。李曉明等[1]將傳統(tǒng)奇異譜分解結(jié)合標準PARAFAC 張量分解方法進行擴展,對機械故障特征進行提取。苗育茁等[2]利用連續(xù)小波變換構(gòu)造3 階張量,通過PARAFAC 對其進行分解,提出了一種多尺度平行因子分析算法,可以有效地從機械非線性多故障狀態(tài)中提取特征,進行故障診斷。楊誠等[3]結(jié)合Volterra 模型與PARAFAC 構(gòu)建了故障預測模型,主要解決了PARAFAC 在分解機械非線性系統(tǒng)信號時估計參數(shù)較多的問題。李志農(nóng)等[4]結(jié)合變分模態(tài)分解(Variational Mode Decomposition,VMD)和PARAFAC 各自優(yōu)點,提出了基于VMDPARAFAC欠定盲分離方法,并將其應用到滾動軸承的復合故障特征提取中。孫宜權(quán)等[5]采用自適應PARAFAC 和BSS 算法對柴油機噴油多故障進行診斷。然而,上述方法中的PARAFAC 分解都是通過構(gòu)造3階張量完成的,采用三線性PARAFAC進行機械故障診斷時,只能對振動信號的部分信號建模,存在信息不完整的問題。在平行因子的發(fā)展過程中,四線性PARAFAC 的提出具有重要的意義。四線性PARAFAC具有三線性平行因子所不具有的優(yōu)勢,且采用四線性平行因子盲分離算法可有效地對機械多故障進行源數(shù)估計,更好地分解信號,提取故障特征[6]。然而,在研究機械多故障欠定盲分離時,通常情況下對四線性PARAFAC 模型采用QALS 迭代擬合,而在欠定條件下,收斂過程中會出現(xiàn)陷入局部收斂的問題,得到的估計源信號往往不是很理想。
集成經(jīng)驗模態(tài)分解(Ensemble Empirical Mode Decomposition,EEMD)是針對經(jīng)驗模態(tài)分解的不足而提出的1 種噪聲輔助數(shù)據(jù)分析方法,該方法充分利用白噪聲均值為零的特點,使得由于干擾導致的任何尺度的信號所出現(xiàn)間斷,都能得到白噪聲的補充,使間斷信號在相應尺度形成連續(xù)信號,該方法很好抑制了由于 EMD(Empirical Mode Decomposition,EMD)分離所導致各分量之間出現(xiàn)混頻現(xiàn)象[7]。文獻[8]結(jié)合EEMD和具有自適應增長特性的輸出隱藏反饋Elman網(wǎng)絡對滾動軸承進行診斷。文獻[9]將EEMD 應用于機械故障中的復雜信號處理,提取故障特征。文獻[10]提出1 種改進的EEMD 方法,以消除在EEMD 方法中只添加噪聲而導致的局限性,結(jié)果表明所提方法可以抑制機械信號模態(tài)混淆并且在故障診斷方面效果明顯。文獻[11]將EEMD 和散布熵結(jié)合,構(gòu)建故障信號的高維特征,在結(jié)合LPP-KNN 進行故障診斷。文獻[12]將集合經(jīng)驗模態(tài)分解(EEMD)和低相干K-SVD相結(jié)合進行齒輪故障特征提取。上述研究均表明EEMD在進行機械振動信號分解時具有獨特的優(yōu)勢。
在此,結(jié)合四線性平行因子盲分離算法和集合經(jīng)驗模態(tài)分解算法(EEMD)的的獨特優(yōu)勢,提出了一種基于EEMD分解的四線性PARAFAC欠定盲源分離方法。該方法首先利用EEMD分解傳感器所采集的觀測信號,接著從分解得到的IMF 分量中選出恰當相關(guān)IMF分量信號。根據(jù)選出的相關(guān)IMF分量與原觀測信號重新構(gòu)造信號,使得經(jīng)四線性分解處理的重組信號數(shù)大于或等于源信號數(shù),這樣盲分離中的欠定就被轉(zhuǎn)換為正定或超定。最后利用四線性交替最小二乘法迭代(Quadrilinear Alternating Least Squares,QALS)進行擬合迭代,得到混合矩陣估計,用最短路徑法得到源信號估計。然后,通過仿真和實驗研究以驗證該方法的有效性。
1 EEMD-四線性平行因子盲分離方法
信號線性混疊模式可以表示為如下形式:
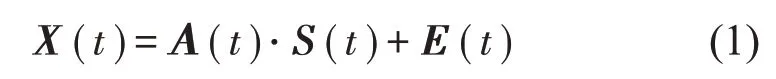
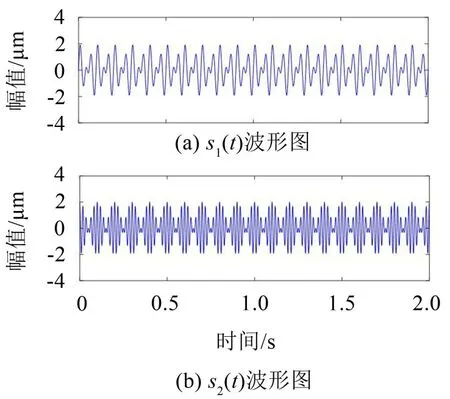
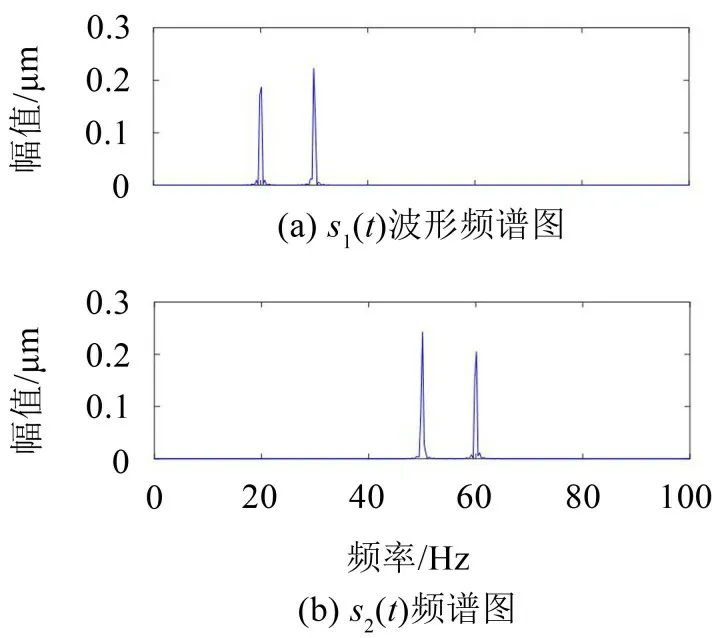
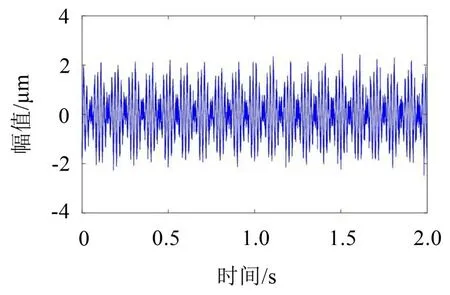
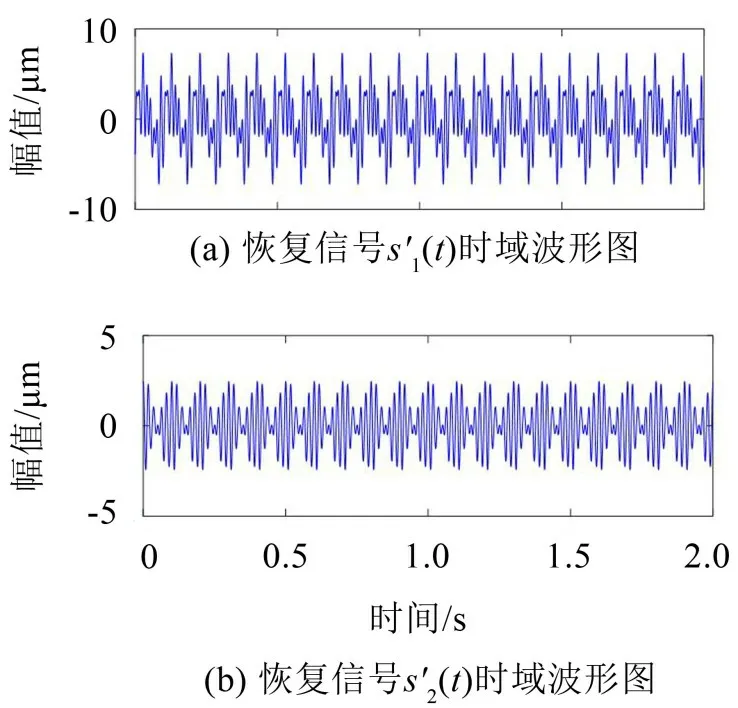
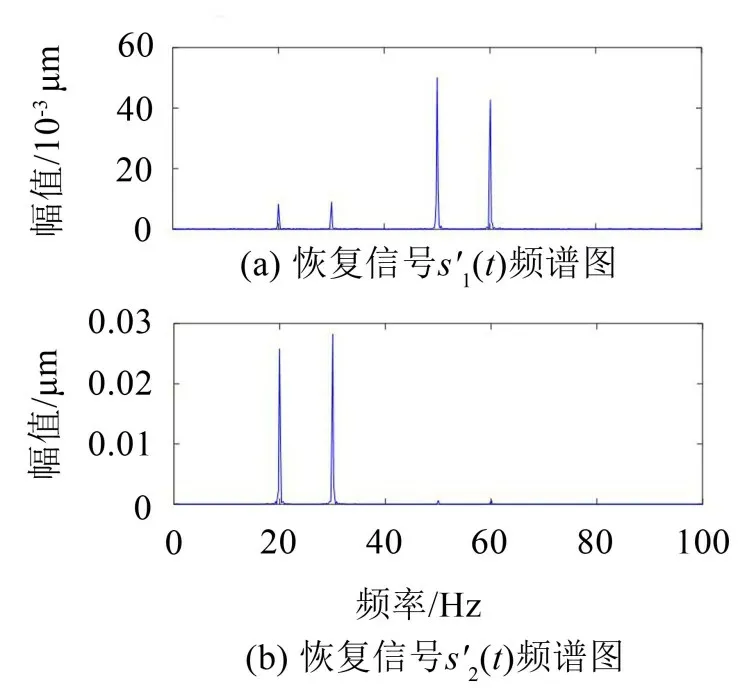
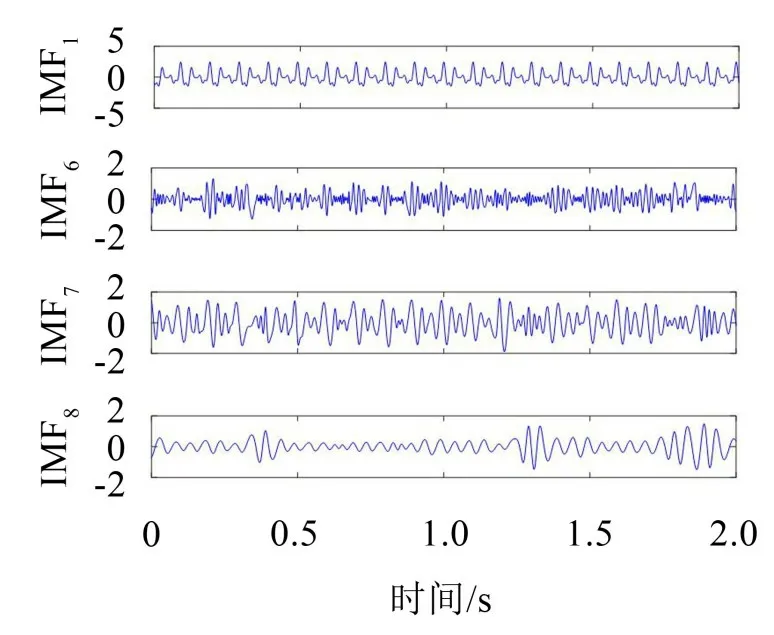
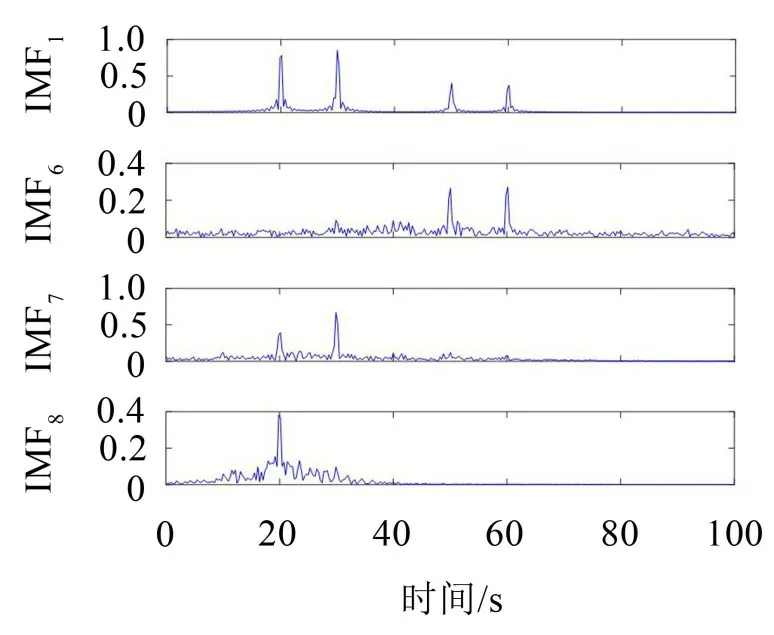
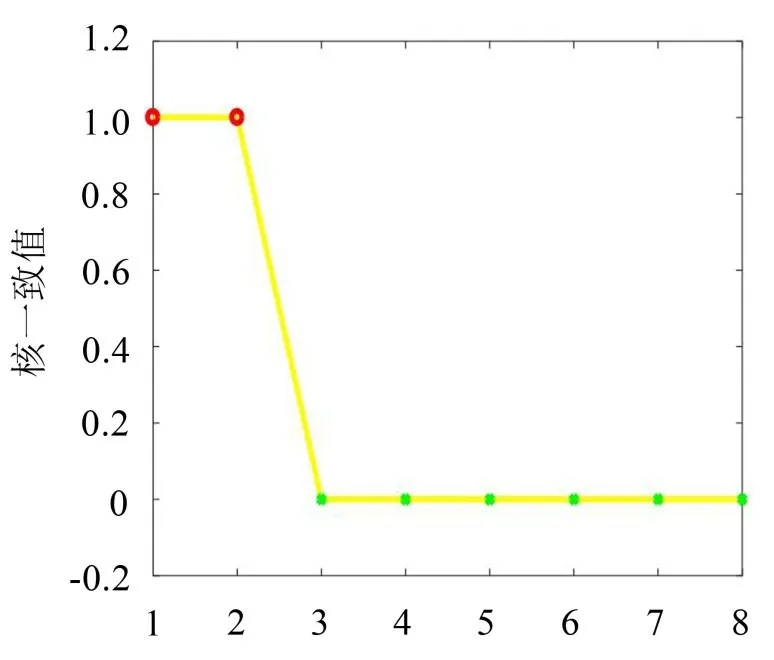
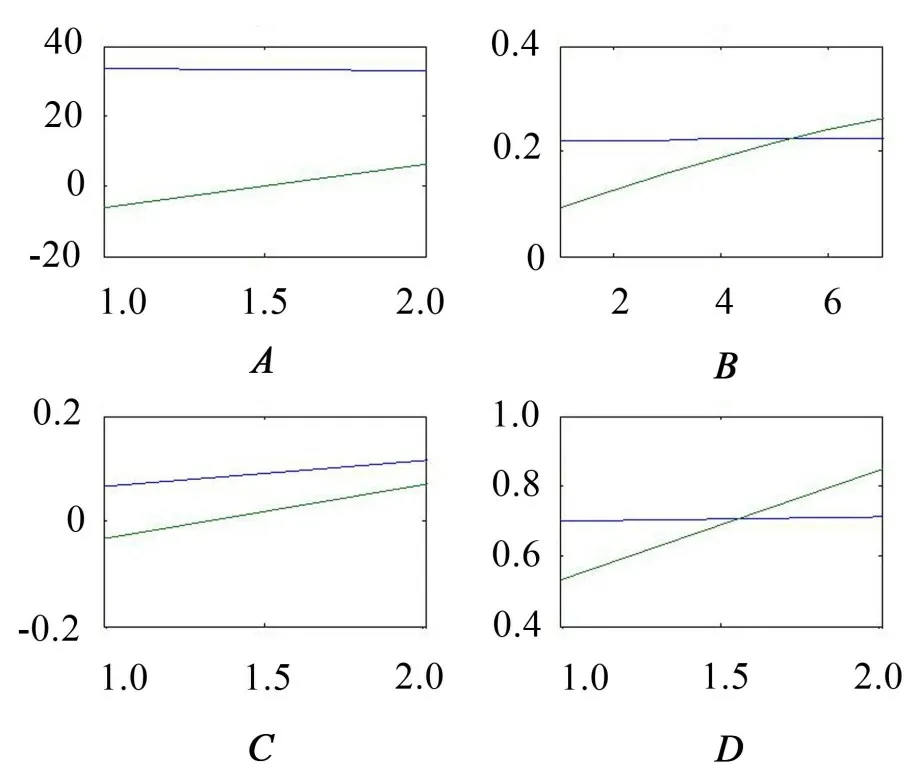
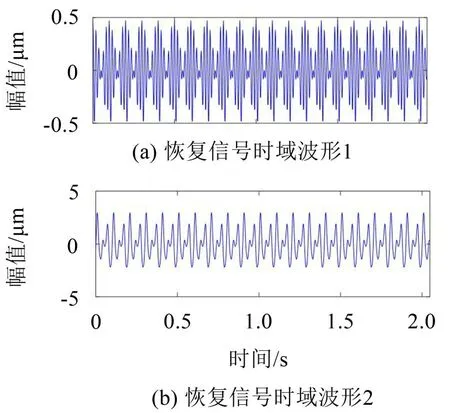
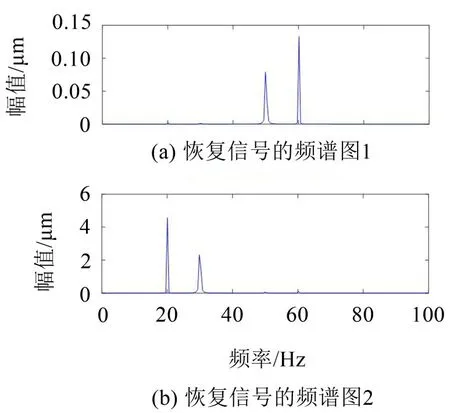
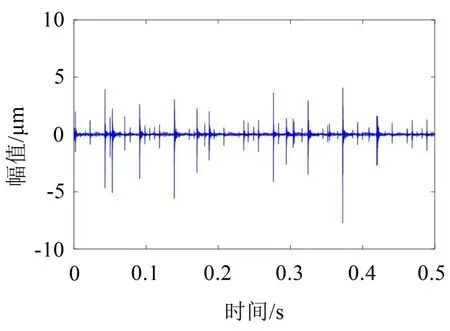
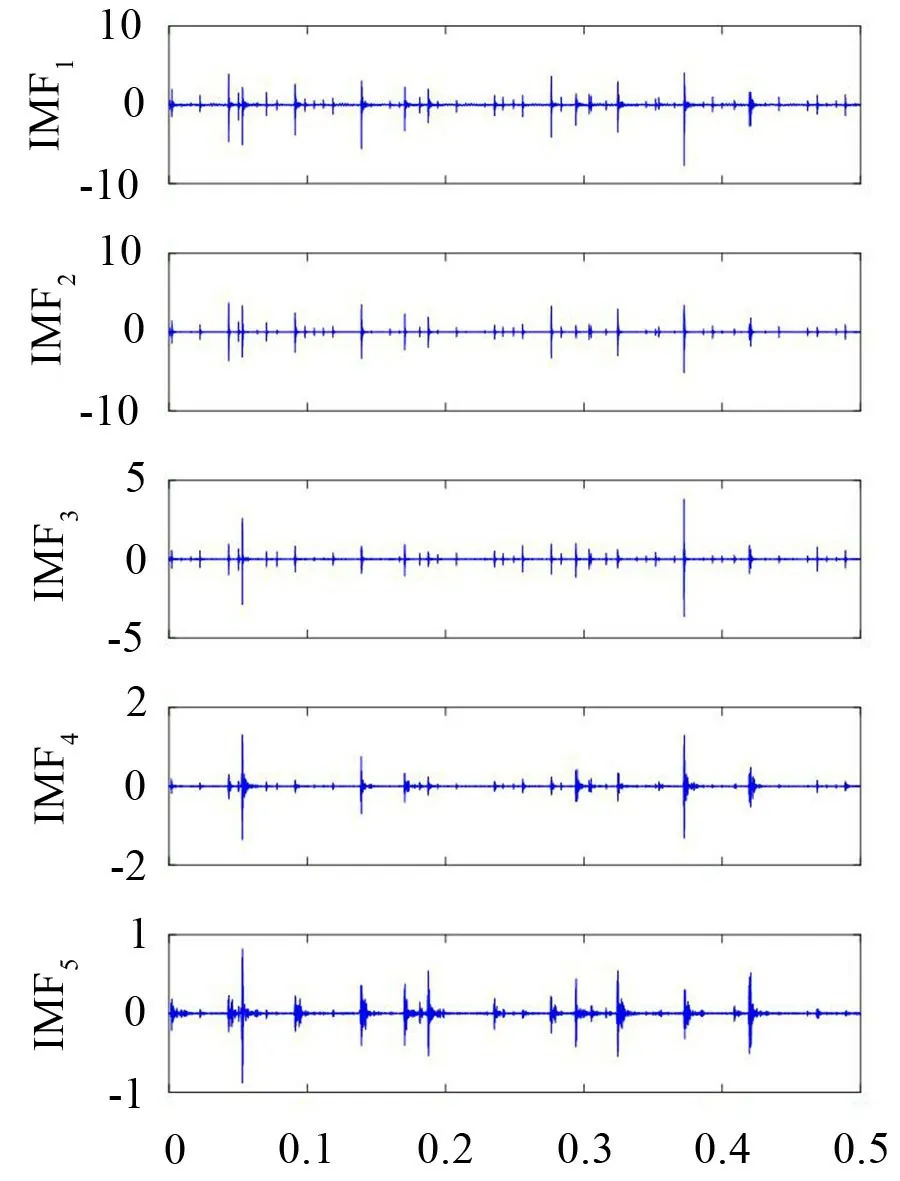
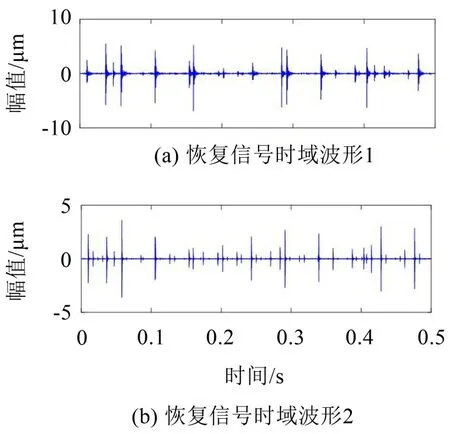
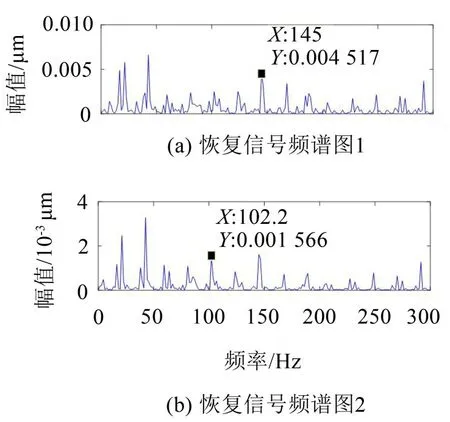
式中:S(t)=[s1(t),…,sM(t)]T為源信號矩陣,每個源信號包含L個數(shù)據(jù)點,A(t)是N×M維的混合矩陣(N 在觀測信號X(t)中加入白噪聲信號,利用EEMD方法將含噪的觀測信號分解成多個IMF信號分量。具體步驟如下: 第一步:首先在處理觀測信號X(t)=[x1(t),…,xN(t)]T前設定平均處理次數(shù)M,其中i=1,2…,M; 第二步:接著在觀測信號X(t)添加白噪聲ni(t),將加入白噪聲的信號作為一個整體,然后與原觀測信號組成新的觀測信號Xi(t)=X(t)+ni(t); 第三步:用EMD分解Xi(t)得到IMF,得到子分量ci,n(t); 其中:ri,n(t)是得到的殘余分量; 第四步:重復前面3個步驟,通過分解得到新的一系列的IMF; 第五步:對得到的IMF 分量進行M次平均獲得cn(t); 其中:i=1,2…,M;n=1,2…M。 第六步:利用相似系數(shù)公式求通過分解得到的IMF 分量相關(guān)系數(shù),然后選取相關(guān)性較大的有效IMF。 選取相關(guān)性較強的IMF 信號分量,并將其與原來的傳感器數(shù)據(jù)組合,構(gòu)建新的觀測信號X(t)。這樣,實現(xiàn)了將欠定條件下的盲源分離轉(zhuǎn)化為正定或超定條件下盲源分離。然后將經(jīng)中心化處理后的觀測信號進行分段處理,其被均勻劃分成J個不會重疊的數(shù)據(jù)段,經(jīng)計算可知每段的數(shù)據(jù)點數(shù)為L/J個,記其為K,即K=L/J,具體段數(shù)可以任意選擇,若最后一段的點數(shù)不夠,可以補零。每一個數(shù)據(jù)段對應的采集時間為h,則其共被分為t/h個時間段,記其為I,此時: 信號塊的時滯協(xié)方差矩陣為: 其中:k=1,2,…,K,序號tk表示t內(nèi)第k個數(shù)據(jù)點。 傳感器在h段采集到的各源信號數(shù)據(jù)時滯協(xié)方差Rn可以通過計算得到,有: 式(6)中:tk表示t內(nèi)第k個源信號。將塊時滯協(xié)方差矩陣轉(zhuǎn)換成為對角陣,并且使該矩陣等于矩陣B,將源時滯協(xié)方差矩陣轉(zhuǎn)換成為對角矩陣并且使該矩陣等于矩陣C,則式(5)、式(6)可以分別改寫為式(7)和式(8)。 將源時滯協(xié)方差矩陣以及塊時滯協(xié)方差矩陣疊加,疊加后所得的3階矩陣計為RJ,K 其中:n=1,2,…,N,k=1,2,…,K。 相鄰對角陣相乘可以換位,則式(9)可表示為: 將式中N×K個切片累積成N×J×K×I維的R(四維數(shù)據(jù)集)。 其 中:n=1,2,…,N,k=1,2…,K,j=1,2,…,J,i=1,2,…I,式(11)即為所構(gòu)造的EEMD-四線性盲分離模型。 如上實現(xiàn)了集合經(jīng)驗模態(tài)四線性平行因子盲源分離算法的構(gòu)建,其分解過程中采用QALS 得到混合矩陣估計A′。分解算法的主要思想為讓上一次估計更新的矩陣參與下一次的矩陣求解,同時使根據(jù)最終估計得到的4個載荷矩陣與被分解矩陣的差值盡量最小,迭代過程步驟分為4步。 第二步:將A重新代入式(12),接著最小化式(12)得到估計的,令其等于B,更新矩陣B。 第三步:將求得的矩陣B重新代入式(12),接著最小化式(12)得到矩陣估計,令其等于C,更新矩陣C。 第四步:將按照以上循環(huán)步驟得到的載荷矩陣代入式(17),若滿足式(17),則退出,反之繼續(xù)。 一般認為ε為1×10-6,??3是殘余誤差的平方和,表示含噪的切片,‖?‖F(xiàn)為Frobenius 范數(shù),i=1,2,…,I,j=1,2,…,J,上標+為Moore-Penrose偽逆,和表示A、B和C的上一次估計,m為迭代次數(shù)。 當式(17)所示的停止準則得到滿足即表示矩陣更新結(jié)束算法收斂,得到最終的混合矩陣估計A′,令A′=A。 令ai為A第i個列向量,si(t)表示源信號的第i個源向量。線性混疊模型X(t)=AS(t)可以表示為: 其中:X(t) 是觀測信號,它可以表示成a1s1(t)、a2s2(t)、…、ansn(t)的累加。ai表示矢量方向,si(t)表示向量長度。對于欠定混合的情況,采用最短路徑法[9]恢復源信號。推斷源的問題可以用式(19)表示: 由式(18)以及式(19)即可得到源信號估計。其主要思想是求每個時刻最優(yōu)解,然后得到恢復的源信號。 構(gòu)造的兩個仿真信號s1(t)、s2(t)如式(20)所示,式中:f1=20 Hz,f2=30 Hz,f3=50 Hz,f4=60 Hz。 選取采樣頻率fs=5 000 Hz,采樣點數(shù)N=20 000。繪制兩個源信號s1(t)、s2(t)的時域波形如圖1所示。相應的頻譜如圖2所示。 圖1 源信號時域波形圖 圖2 源信號頻譜圖 用1×2 維的隨機混合矩陣A,將兩個源信號s1(t)、s2(t)進行隨機混合,混合后得到1 路的混合信號如圖3所示。已知源信號的個數(shù)為2,混合后觀測信號的個數(shù)為1,因此,該盲源分離問題為欠定求解問題。 圖3 混疊信號時域波形圖 利用四線性平行因子盲分離算法將該混合信號分離,得到恢復源信號如圖4 所示。相應的頻譜如圖5所示。 圖4 恢復信號時域波形圖 圖5 恢復信號的頻譜 對比圖4和圖1可知,采用四平行因子盲分離算法得到的恢復信號與源信號相似度不是特別高,分離效果不理想。由圖5 可知,分離得到的恢復信號的特征頻率分別為20 Hz、30 Hz、50 Hz、60 Hz,與源信號特征頻率不一致,分離得到的頻譜圖效果不是很理想,因此,在欠定條件下直接采用四線性平行因子盲源分離算法分解效果不理想,需對其進一步改進。 為了改進四線性平行因子盲源分離算法的這種不足,用集合經(jīng)驗模態(tài)平行因子盲源分離算法分解混合信號。該算法首先用EEMD 算法分解混合信號,通過分離得到14 個子分量,然后選擇相關(guān)子分量。選擇相關(guān)分量的具體做法是利用相關(guān)系數(shù)求各子分量與觀測信號的相關(guān)度,一般認為信號與觀測信號越相似,則相關(guān)度的值越接近為1。根據(jù)相關(guān)度的值定義其在0 到0.3 之間為微相關(guān),0.3 到0.5 之間為實相關(guān),0.5到0.8之間為顯著相關(guān),0.8到1之間為高度相關(guān)。根據(jù)EEMD 算法分解得到的14 個子分量的相關(guān)系數(shù)如表1所示。 由表1可知,子分量IMF1、IMF6、IMF7、IMF8的相關(guān)系數(shù)值相對較高,其他分量均為不相關(guān),所以選擇IMF1、IMF6、IMF7、IMF8為相關(guān)分量并將其與原觀測信號組合得到新觀測信號,這樣就將欠定轉(zhuǎn)化為超定。繪制相關(guān)分量IMF1、IMF6、IMF7、IMF8的時域波形圖和頻譜圖,得到的圖形分別如圖6 以及圖7所示。 圖6 根據(jù)EEMD分解得到相關(guān)子分量時域波形圖 圖7 根據(jù)EEMD分解得到相關(guān)子分量的幅值譜圖 表1 各子分量相關(guān)系數(shù) 將通過分解得到相關(guān)子分量和混疊信號組合,得到新觀測信號,用核一致算法估計振源數(shù),如圖9所示。 圖9 組件數(shù) 由圖9可知,振源數(shù)為2。將得到的觀測信號用四線性平行因子盲分離算法處理,用QALS 算法擬合迭代,當達到迭代終止條件時得到4 個載荷矩陣A、B、C、D。由圖8 可知,4 個載荷矩陣中,載荷矩陣B、D分解形式相同,表明建立的模型符合式(11)所示的四線性模型,并未偏離四線性模型。 圖8 載荷矩陣 用集合經(jīng)驗模態(tài)四線性平行因子盲源分離算法處理通過組合得到的觀測信號,依據(jù)模型求得混合矩陣估計,以及根據(jù)式(19)求得估計源信號,繪制恢復信號的時域波形圖如10 圖所示。相應的恢復信號頻譜如圖11所示。 由圖11 可知,圖11(a)中的特征頻率分別為50 Hz、60 Hz,圖11(b)中的特征頻率分別為20 Hz、30 Hz,除排列順序有所不同外,其分別與兩源信號的特征頻率相一致,這種排列順序改變并不影響分離結(jié)果的正確性。對比圖10與源信號時域波形,恢復信號的時域波形圖和源信號時域波形圖非常相似。由此可知,提出的方法能夠有效分離混合信號,分離效果非常令人滿意。對比提出的方法和傳統(tǒng)的四線性平行因子盲源分離算法,發(fā)現(xiàn)欠定條件下采用四線性平行因子盲源分離算法并不能得到很好的分離效果,而采用集合經(jīng)驗模態(tài)四線性平行因子盲源分離算法可以很好分離混合信號并且分離效果比四線性平行因子盲源分離算法好很多,證明了該算法的有效性。 圖10 恢復信號時域波形 圖11 恢復信號的頻譜圖 為了驗證所提算法的有效性,將集合經(jīng)驗模態(tài)四線性平行因子盲分離算法應用于滾動軸承復合故障盲源分離中。實驗所需要的數(shù)據(jù)由滾動軸承診斷試驗臺采集,試驗臺由旋轉(zhuǎn)電機、滾子軸承和加速度傳感器組成。軸承的代號是N205EM。電機轉(zhuǎn)速約為1 300 r/min,轉(zhuǎn)動頻率約為21.7 Hz,采樣頻率fs=100 kHz。數(shù)據(jù)中包含一組內(nèi)滾道和滾子的復合故障信號。使用線切割機技術(shù)人為制造缺陷以產(chǎn)生故障源,內(nèi)圈故障大小為0.3 mm×0.15 mm,滾子故障大小為0.3 mm×0.15 mm,利用軸承故障頻率機理公式可計算得到滾子的故障特征頻率fb=102.3 Hz,內(nèi)圈故障特征頻率fi=145.7 Hz。所用信號的采樣點數(shù)為1 001 000,繪制采集的混合觀測信號時域波形圖,如圖12所示。 圖12 觀測信號時域波形圖 將觀測信號用EEMD 算法分解,得到16 個IMF分量。利用相關(guān)系數(shù)法選擇相關(guān)性較大的子分量,各子分量的相關(guān)系數(shù)如表2所示。 由表2 可知,子分量IMF1、IMF2、IMF3、IMF4、IMF5的相關(guān)系數(shù)均大于0.3,為有效子分量,其他子分量信號的相似系數(shù)值均在0.3 以下,所以選擇IMF1、IMF2、IMF3、IMF4、IMF5為相關(guān)分量。將選擇的相關(guān)子分量與原觀測信號組合得到新的觀測信號。繪制IMF1、IMF2、IMF3、IMF4、MF5的時域圖,得到的圖形如圖13所示。 表2 各子分量相關(guān)系數(shù) 圖13 采用EEMD分解觀測信號得到的有效子分量時域波形圖 將分解得到的這5個相關(guān)的子分量信號和混疊信號重新構(gòu)造成新的觀測信號,計算觀測信號段的時滯協(xié)方差矩陣,并將所有數(shù)據(jù)段的時滯協(xié)方差疊加成4階張量形式,得到四線性模型,用QALS擬合,當滿足式(17)時迭代結(jié)束,求得估計矩陣。利用所求的估計矩陣和最短路徑法得到恢復信號,繪制恢復信號的時域圖和頻譜如圖13、圖14所示。 圖14 恢復信號時域波形圖 由圖14可知,采用集合經(jīng)驗模態(tài)四線性平行因子盲源分離算法可以有效分離出滾動軸承內(nèi)圈故障和滾動體故障。分離得到的幅值譜如圖15 所示。圖15(a)中特征頻率有145 Hz以及相應的調(diào)制頻率,對比計算得到的故障特征頻率,發(fā)現(xiàn)其與軸承內(nèi)圈故障特征頻率145.7 Hz 基本一致。圖15(b)中的特征頻率有102.2 Hz 以及相應的調(diào)制頻率,對比計算所得的故障特征頻率,發(fā)現(xiàn)其與計算所得的軸承的滾子故障特征頻率102.3 Hz基本一致。 圖15 恢復信號頻譜圖 由此可知,運用集合經(jīng)驗模態(tài)四線性平行因子盲源分離算法可以有效分離出滾動軸承復合故障,取得了非常滿意的分離效果,實驗證明了該方法的有效性。 四線性平行因子是三維平行因子的拓展模型,通過其可以獲得更多的信息,并在寬松的約束條件下其模型分解也具有唯一性。通過集合經(jīng)驗模態(tài)分解可以對時間序列進行局部平穩(wěn)化處理,適用于任何信號分解,可以解決盲源分離中的欠定問題,基于此,將四線性平行因子和經(jīng)驗模態(tài)分解相結(jié)合,提出一種基于集合經(jīng)驗模態(tài)和四線性平行因子欠定盲分離算法,所提算法利用EEMD重構(gòu)觀測信號,將欠定轉(zhuǎn)換為超定和正定,再使用四線性平行因子對觀測信號進行處理,得到源信號的估計。仿真結(jié)果表明,采用提出的方法不僅能準確估計出源信號數(shù)目,而且還能估計出源信號。最后,將提出的方法應用到滾動軸承復合故障診斷中,實驗結(jié)果進一步驗證了提出的方法的有效性,內(nèi)圈故障和滾子故障的特征頻率及相應的調(diào)制頻率都得到了充分的反映。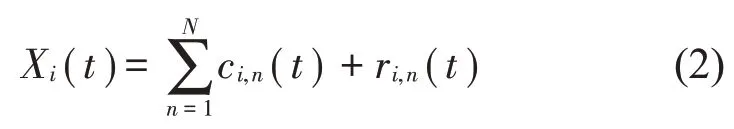

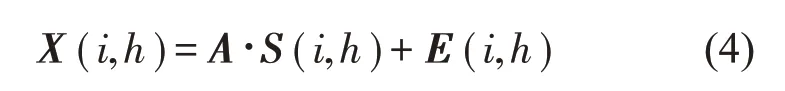
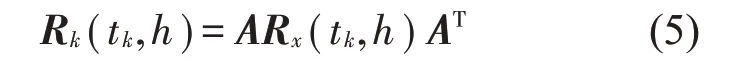
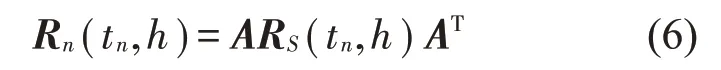
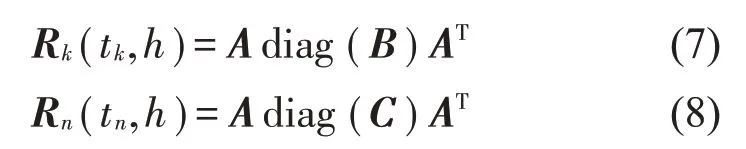
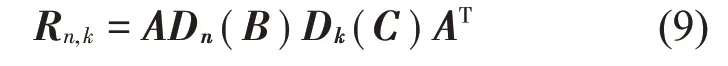
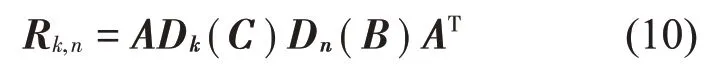
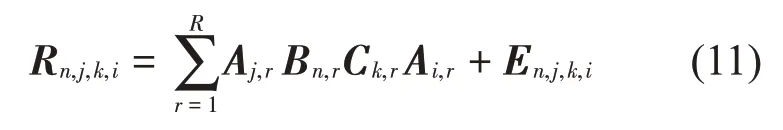

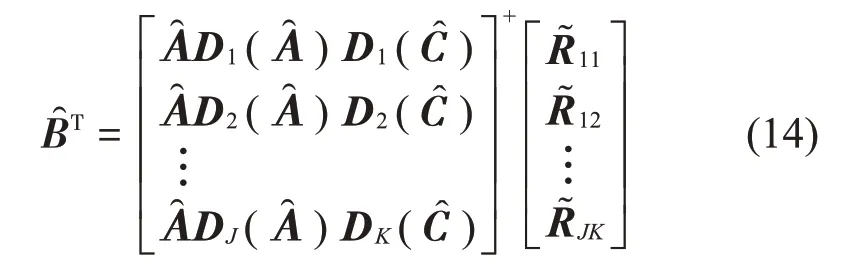
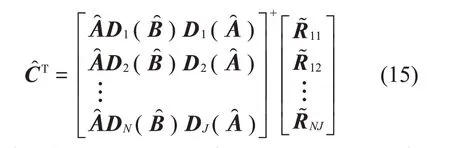
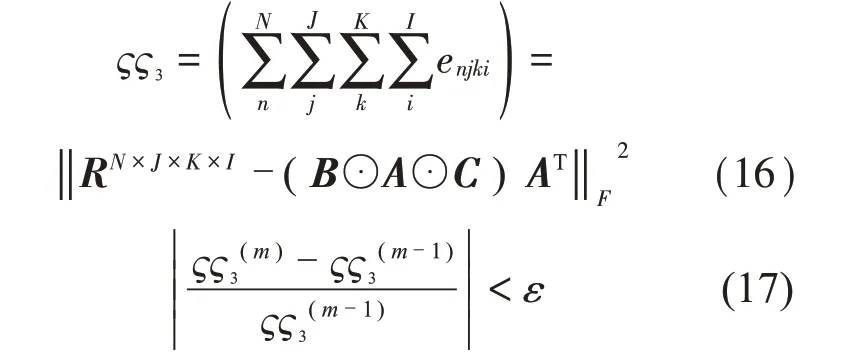
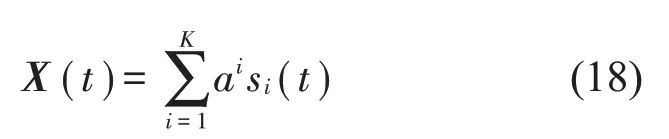
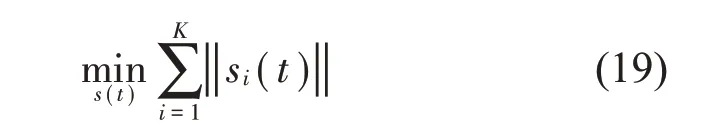
2 仿真研究
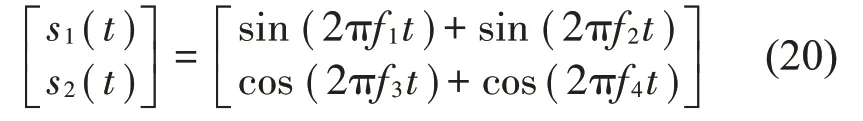

3 實驗研究

4 結(jié)語

