機車齒輪箱齒根裂紋故障特征提取方法研究

劉新廠，孫 琦，藺渝鴻

(1.成都工業學院 汽車與交通學院，成都 611730；2.西南交通大學 機械工程學院，成都 610031)

齒輪箱齒輪傳動系統將牽引電機的扭矩傳遞給輪對驅動列車運行，是機車的重要組成部分[1－2]。齒輪箱齒輪傳動系統工作條件十分惡劣，不僅受到傳遞載荷、齒輪嚙合所致的周期性內部激勵以及輪軌界面激勵影響，而且還要適應輪對、構架之間復雜的相對運動。在列車運營條件下，齒輪箱系統一旦發生故障，故障就會快速發展和蔓延，若不及時發現故障并采取相應措施，會導致齒輪箱的箱體破壞、齒輪斷裂、軸承燃燒、動力傳遞中斷以及車毀人亡等重特大事故的發生，嚴重危及行車安全。2006年，我國對運行62萬公里后SS4改型機車進行檢修時發現多起牽引從動齒輪產生裂紋和崩齒問題[3]。2008 年，葡萄牙鐵路公司2600 系列機車變速箱殼體產生裂紋[4]。因此，齒輪箱齒輪傳動系統故障檢測與診斷研究是保證列車安全運行的關鍵。

基于振動信號分析的機械結構損傷診斷方法是一種最普遍以及常用的方法[5]。但是實際采集到的振動信號大多存在調制現象并且信號中含有的故障信號十分微弱，同時含有大量的噪聲。

國內外學者在信號解調方面做了大量研究。1982 年，國外學者Randall[6]采用高通絕對值解調方法對齒輪箱故障進行監測與診斷。文獻[7]中作者采用希爾伯特包絡解調方法對含有疲勞裂紋故障信息的機械系統振動信號進行處理，很好提取了信號中所含有的故障信息。1996年，Ma等[8]為了更好地檢測齒輪缺陷，提出了一種基于模型的解調方法，該方法可以提取齒輪振動信號中所包含的信息。2001年，Wang[9]提出了一種利用共振解調技術對齒輪齒面裂紋進行早期檢測的方案。該方法中首先運用同步信號平均值法去除規則的齒輪嚙合諧波，生成殘余信號。然后，通過共振解調技術對殘差信號解調。最后，利用一些統計量對齒輪是否存在故障進行診斷。2005年，Smith[10]提出了一種新的分解方法即局部均值分解法對調幅和調頻信號進行解調處理。2010年，Liang等[11]提出了一種與參數無關但易于實現的旋轉機械故障檢測技術即Teager能量算子解調法，運用該方法對具有調制現象的機械系統振動信號進行處理，實現了對信號的幅值以及頻率的解調，成功對系統故障進行檢測。同年，Cheng等[12]針對齒輪振動信號在升、降速過程中的調制特性，提出了一種基于廣義解調時頻分析和包絡階次譜技術相結合的故障診斷方法，并將其應用于齒輪振動信號的瞬態分析中。2015年，Jin等[13]采用循環自相關方法對具有調制特性的齒輪箱振動信號進行解調處理，取得了較好的效果。2017年，An等[14]提出了一種基于變分模態分解和包絡分析的齒輪故障診斷方法。首先，其運用變分模式分解法將復雜的信號分解成幾個穩定的分量；然后，采用包絡解調法對得到的各分量進行了分析。

在過去的幾年中，圖譜理論在流形學習以及圖信號處理領域取得了巨大進展[15－16]。近些年，一些學者開始將圖譜理論算法應用到旋轉機械故障診斷領域。在2016 年，Ou 等利用圖傅里葉變換(Graph Fourier Transform，GFT)方法提取旋轉軸承振動信號中的沖擊成分，實現了軸承故障檢測[17]。但是，經過圖傅里葉變換之后高斯白噪聲信號會有很多成分集中在圖譜域的高階區域，所以當信號中含有較強的噪聲時，在進行圖譜傅里葉變換后提取到的沖擊成分會受到噪聲的影響，影響分析結果。

基于以上原因本文提出了一種基于復Morlet小波梳狀濾波器以及圖譜理論相結合的齒輪箱傳動系統齒根裂紋故障診斷方法。首先，構造復Morlet 小波簇梳狀濾波器，通過復Morlet 小波簇梳狀濾波器對包含齒輪箱齒根裂紋信息的故障信號進行包絡解調處理，達到對信號進行去噪以及解調處理的目的；然后通過圖譜傅里葉變換方法將信號中含有的沖擊分量集中到圖譜域的高階區域，從而有效提取信號中的沖擊成分，對齒輪箱齒根裂紋故障診斷提供有力依據。從仿真信號處理結果中可以看出，本文提出方法能夠凸顯故障信號并且提高故障頻率信號的信噪比。

1 GFT 以及復Morlet 小波簇梳狀濾波器

1.1 復Morlet 小波簇梳狀濾波器及包絡解調方法原理

具有梳狀濾波器特性的復Morlet小波簇構造方法[18]如式(1)所示，式(1)的傅里葉變換結果如式(2)所示：

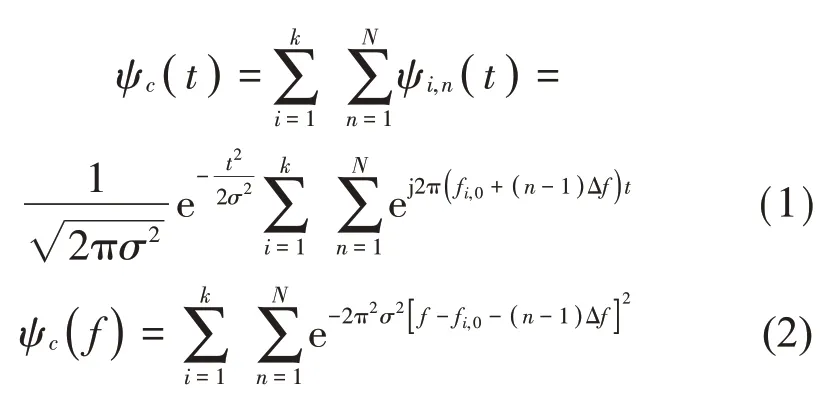
式(1)中參數k表示構造的復Morlet小波簇梳狀濾波器中含有的通帶的個數，fi,0為構成梳狀濾波器的第i個通帶的起始頻率。具有梳狀濾波特性的復Morlet小波簇時域波形的實部以及虛部如圖1至圖2所示。此梳狀濾波器具有5 個濾波器通帶，每個通帶的起始頻率分別為15 Hz、35 Hz、55 Hz、75 Hz、95 Hz，帶寬參數σ=0.25，復Morlet 小波個數N=11，相鄰復Morlet小波中心頻率的間隔?f=1。具有梳狀濾波特性的復Morlet小波簇頻譜圖如圖3所示。

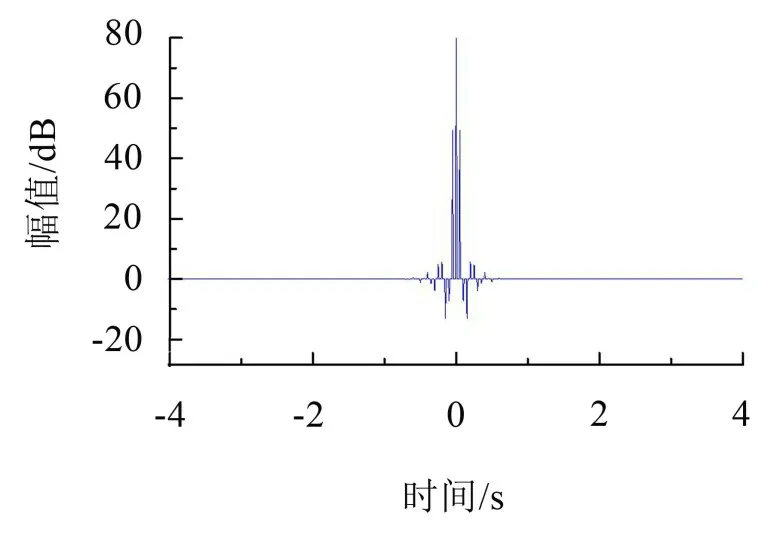
圖1 具有梳狀濾波特性的復Morlet小波簇時域波形的實部

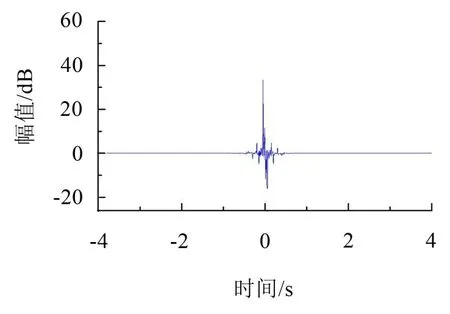
圖2 具有梳狀濾波特性的復Morlet小波簇時域波形的虛部

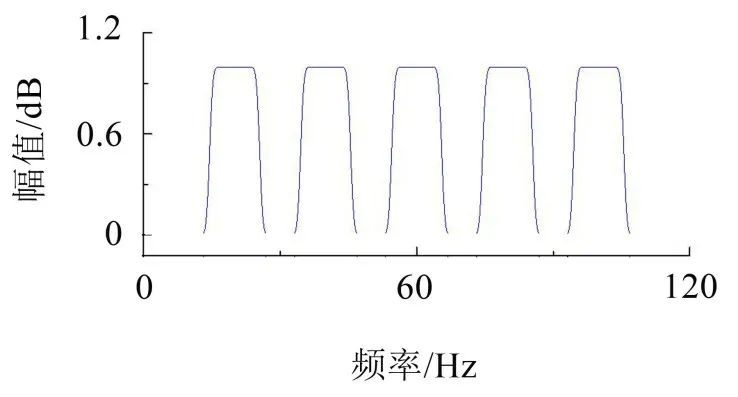
圖3 具有梳狀濾波特性的復Morlet小波簇頻譜圖

通過以上分析可得復Morlet小波簇梳狀濾波器是由若干個復Morlet 小波簇按照一定的規則組合而成的，由于復Morlet小波簇具有包絡解調的功能，所以復Morlet小波簇梳狀濾波器同樣具有包絡解調功能。并且由于復Morlet小波簇梳狀濾波器的帶通功能使得處理后的信號中噪聲成分衰減，從而可減少噪聲的影響。

1.2 圖傅里葉變換理論

機械振動信號、諧波信號等時間序列信號具有路圖的結構，所以這些信號可以運用路圖信號G={V，E，W}的表達方式進行表示。V={v1,v2,v3,…,vN}是頂點的集合，N是振動信號個數，E={e1,e2,e3,…,eN}是邊的集合，W是一個鄰接矩陣，用來存放頂點間的關系。wij是W中第i行第j列的元素，求解公式如式(3)所示。

基于圖傅里葉變換理論變換過程如下所示：

(1)將采集到的機械振動信號運用路圖信號G的表達方式進行表達，求解出參數V、E、W。

(2)求解拉普拉斯矩陣L。L的計算公式如式(4)所示。式中D是度對角矩陣，di為頂點的度數，計算公式如式(5)所示。

(3)對拉普拉斯矩陣L進行標準正交分解，得到拉普拉斯特征值λ1以及特征向量x1，求解公式如式(6)所示。

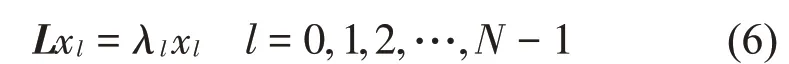
(4)圖信號是一個向量f(n)∈Rn，定義為f(n)：V={v1,v2,v3,…,vN}→Rn(f(1)，f(2)，f(3)，…，f(N))。表示圖信號f(n)的圖傅里葉變換，定義式如式(7)所示：

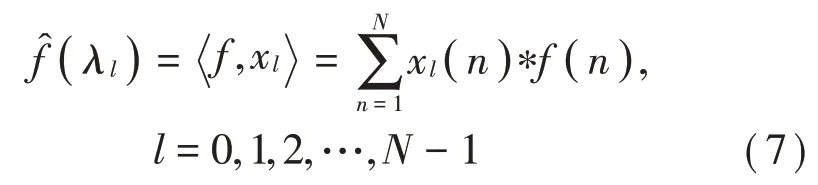
通過圖傅里葉變換方法可以將振動信號中所包含的沖擊成分集中在圖譜域的高階次區域。但是，高斯白噪聲信號經過圖傅里葉變換之后會有很多成分集中在圖譜域的高階區域，所以當信號中含有較強的噪聲時，經圖譜傅里葉變換提取到的沖擊成分會受到噪聲的影響。

一個均方根為0.3的高斯白噪聲的時域圖如圖4(a)所示，高斯白噪聲經圖傅里葉變換后的圖譜如圖4(b)所示。從圖4(b)可以看出高斯白噪聲也具有高頻聚集性。基于以上原因本文提出了一種基于復Morlet小波梳狀濾波器以及圖譜理論相結合的齒輪箱齒根裂紋故障診斷方法。

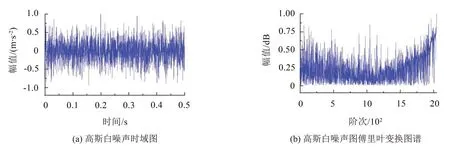
圖4 均方根為0.3的高斯白噪聲的時域圖和GFT圖譜

2 本文的方法

首先，對原始信號進行傅里葉變換得到頻譜圖，根據頻譜圖對信號中的載波頻率以及故障特征頻率進行估計；然后，構造復Morlet 小波簇梳狀濾波器，采用復Morlet小波簇梳狀濾波器對含有齒輪箱齒根裂紋信息的故障信號進行包絡解調處理；最后，通過圖譜傅里葉變換將信號中含有的沖擊分量集中到圖譜域的高階區域，從而對齒輪箱齒根裂紋故障進行診斷。本文提出方法的流程如下所示：

(1)對原始信號進行傅里葉變換得到頻譜圖，根據頻譜圖對信號中的載波頻率以及故障特征頻率進行估計；

(2)構造復Morlet 小波簇梳狀濾波器。根據公式(1)構造復Morlet 小波簇梳狀濾波器，每個帶通濾波器的中心頻率與載波信號及其諧波信號頻率相同，通帶帶寬由故障頻率確定；

(3)對原始信號以及復Morlet 小波簇梳狀濾波器進行傅里葉變換，將求解得到的結果相乘，然后求解傅里葉逆變換即得到復Morlet小波簇變換系數；

(4)包絡信號求解。對求解得到的復Morlet 小波簇變換系數取模即可獲得待分析信號的包絡信號。

(5)提取信號中的脈沖分量。利用GFT 方法可以得到信號的圖譜系數。利用這些圖譜系數在GFT圖譜的高階區域重建不同的脈沖分量。

(6)基于這些脈沖分量對齒輪箱齒輪齒根裂紋故障進行診斷。計算這些脈沖分量的希爾伯特包絡譜，找出故障特征頻率下包絡譜值最大的脈沖分量。然后對沖擊分量進行分析，可以檢測出齒輪箱齒輪齒根裂紋故障。

3 基于機車振動數據的齒根裂紋特征提取方法有效性驗證

本節采用復Morlet小波簇梳狀濾波器以及圖譜理論相結合的方法對機車齒輪箱齒根存在裂紋故障情況下采集到的機車電機振動信號進行分析，對基于復Morlet小波簇梳狀濾波器以及圖譜理論的齒根裂紋故障診斷方法的有效性進行驗證。

對文獻[19]中含齒輪傳動系統的機車垂向動力學模型進行仿真得到機車齒輪齒根存在裂紋情況下的機車電機振動加速度信號。含有齒輪傳動系統的機車軌道耦合垂向動力學模型如文獻[19]中所示，此動力學模型由機車子系統以及軌道子系統組成。機車子系統包含1個車體、2個構架、4個輪對、4個電機以及4個齒輪傳動系統。車體與構架之間通過二系懸掛系統連接；構架與輪對之間通過一系懸掛系統連接；齒輪箱的一端與構架連接，另外一端與輪對連接。機車子系統的各個組成部分具有點頭以及垂向振動兩個自由度。軌道子系統由鋼軌、軌枕、道床、路基組成，它們之間通過彈簧阻尼元件連接。鋼軌被視為一根無限長的Euler梁，它與軌枕之間通過彈簧阻尼元件連接。文獻[19]中給出了道床的建模方法，在這個模型中相鄰軌道板之間加入了剪切剛度以及剪切阻尼。軌道子系統的各個組成部分只具有垂直方向的一個自由度。齒輪傳動系統由電機、小齒輪、大齒輪組成。電機的轉子通過扭簧阻尼元件與小齒輪連接，小齒輪通過嚙合力帶動齒輪旋轉，大齒輪安裝在輪對上。齒輪傳動系統的各個組成部分只有自身旋轉一個自由度。由于機車被視為一個多剛體系統，所以系統的微分方程可以根據D′Alembert準則建立。

仿真過程中機車受到軌道垂向隨機不平順激勵的作用，軌道垂向隨機不平順采用美國六級軌道譜。列車運行速度為100 km/h，采樣頻率為20 kHz。通過仿真得到的機車電機振動信號的時域圖如圖5所示。

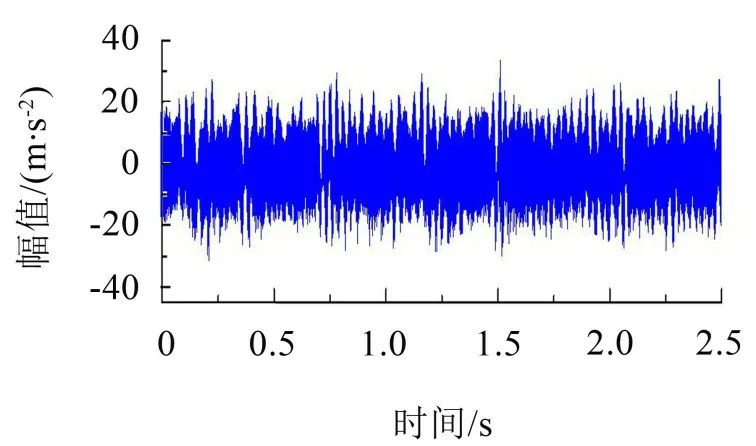
圖5 電機振動加速度的時域圖

根據圖5可知軌道隨機不平順激勵使得通過仿真得到的機車電機振動信號中含有大量噪聲，使得齒根裂紋故障特征頻率淹沒在噪聲中。

將機車電機振動信號進行圖傅里葉變化后所得合成信號的時域圖如圖6所示。將機車電機振動信號進行圖傅里葉變化后所得合成信號的希爾伯特頻譜圖如圖7所示。

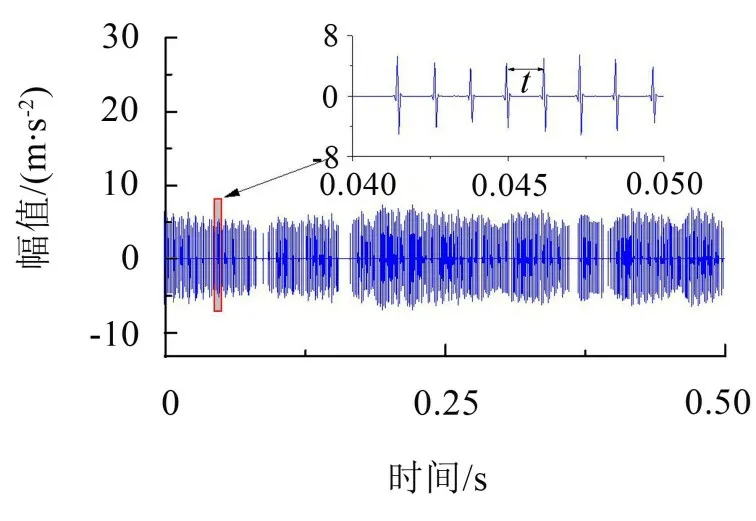
圖6 經GFT處理后合成信號時域圖

對圖6 中的信號進行局部放大，發現相鄰兩個脈沖點峰值之間的時間間隔t與齒輪傳動系統中齒輪嚙合時間間隔相同。對圖7中的信號進行局部放大，發現信號中的小齒輪故障頻率fp十分不明顯，但是大小齒輪的嚙合頻率fm十分明顯。通過分析原因得知，齒輪發生故障的情況下，齒輪故障頻率會產生調制現象，同時齒輪嚙合過程中大小齒輪嚙合所產生的沖擊強度遠遠大于小齒輪故障所產生的沖擊強度，所以求解得到的信號主要含有小齒輪的嚙合頻率及其倍頻成分。因此在對信號進行圖傅里葉變化之前需要對信號進行解調處理。

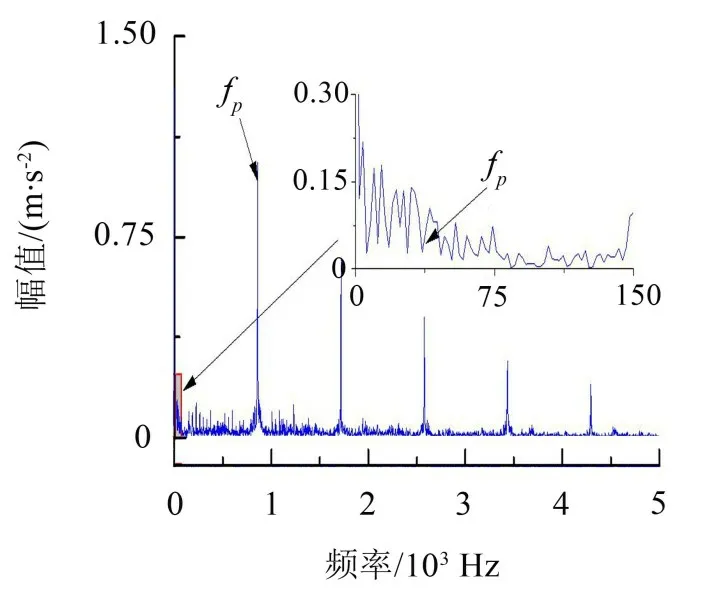
圖7 經GFT處理后合成信號頻譜圖

采用復Morlet小波簇梳狀濾波器以及圖傅里葉變化對機車電機振動信號進行處理，得到的合成信號時域圖如圖8所示，合成信號頻譜圖如圖9所示。

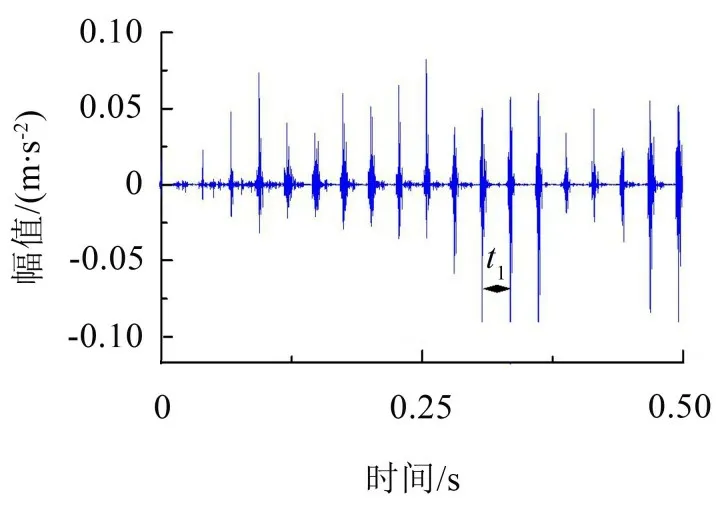
圖8 采用復Morlet小波簇梳狀濾波器以及圖傅里葉變化對信號進行處理后得到的合成信號的時域圖

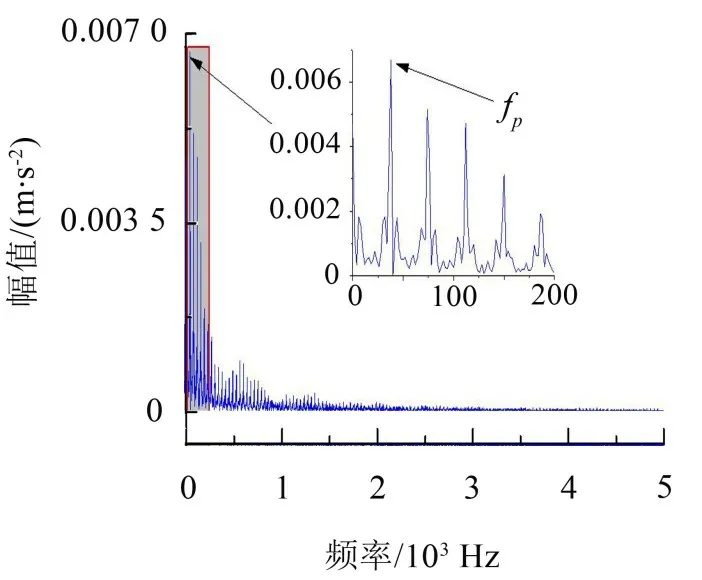
圖9 采用復Morlet小波簇梳狀濾波器以及圖傅里葉變化對信號進行處理后得到的合成信號的頻譜圖

從圖9可以看出相鄰兩個脈沖峰值點之間的距離t1與小齒輪故障時間間隔相等，從圖9中可以較清楚看到信號故障頻率fp。通過圖6 與圖8 的對比可以發現，圖8 中信號的沖擊成分更為明顯；根據圖7可得齒輪故障頻率幅值為0.028 46，信噪比為0.011。圖9 中故障頻率fp的數值為0.006 678，信噪比為0.022 9，雖然圖9中信號的幅值較小，但是信噪比很大，更能凸顯故障信號。通過以上數值的對比可以發現，基于復Morlet 小波梳狀濾波器以及圖譜理論方法的齒輪故障診斷方法能夠較好消除噪聲干擾，凸顯信號中的故障成分。

4 結語

本文采用圖傅里葉變換方法對機車齒輪箱齒根產生裂紋故障情況下振動信號的分析方法進行研究。

(1)針對采用圖譜傅里葉變換提取到的沖擊成分會受到噪聲的影響以及在齒輪箱齒輪含有齒根裂紋的情況下所采集到的振動信號中存在調制現象等問題，提出了一種基于復Morlet 小波梳狀濾波器以及圖譜理論相結合的齒輪箱齒根裂紋故障診斷方法。

(2)將本文提出的方法引入機車齒輪箱齒根裂紋故障診斷中，從分析結果中可以看出本文提出方法能夠凸顯故障信號并且提高故障頻率信號的信噪比。