路面上減速帶對通過車輛振動影響分析

賈常明

（中國刑事警察學(xué)院 刑事科學(xué)技術(shù)學(xué)院，沈陽 110035）

汽車?yán)碚揫1]的平順性部分分析了車輛振動系統(tǒng)單自由度模型和二自由度模型的頻率響應(yīng)函數(shù)的穩(wěn)態(tài)解，利用了車輛振動系統(tǒng)的幅頻特性討論了共振頻率、阻尼比、質(zhì)量比和剛度系數(shù)比對車輛振動的影響。針對不同形狀和尺寸的減速帶對通過車輛振動的影響，文獻(xiàn)[2－4]利用車輛動力學(xué)仿真軟件(ADAMS/CAR)和實車試驗研究，得出了車身振動加速度隨車速增大而增加的結(jié)論，而文獻(xiàn)[5－7]利用車輛動力學(xué)仿真軟件（TrukSim 和MATLAB/Simulink）和實車試驗研究，得出了車身振動加速度并非隨車速增大而增大的結(jié)論。以上二者產(chǎn)生差異的原因可能是采用的模型不同和有關(guān)參數(shù)不同引起的，其中使用MATLAB等有關(guān)軟件直接在時域得出振動微分方程的數(shù)值解，物理意義不突出。車輛通過減速帶的振動效果與車輛振動系統(tǒng)的頻率響應(yīng)函數(shù)有關(guān)，如車身共振頻率、車輪共振頻率等，車速的大小影響減速帶對車輪作用的時間頻譜分布。本文在汽車?yán)碚揫1]中車輛振動系統(tǒng)的二自由度模型和有關(guān)參數(shù)基礎(chǔ)上，將車輛振動系統(tǒng)的頻率響應(yīng)函數(shù)與減速帶對車輛作用的時間頻譜函數(shù)的乘積進行逆傅里葉變換，得出車輛振動與時間關(guān)系的瞬態(tài)解，可以形象看到不同車速下振動效果及影響因素。

1 車輛二自由度模型

車輛振動系統(tǒng)的二自由度振動模型如圖1 所示，其中，m2是車身質(zhì)量，z2是車身離開平衡點的位移，C是減振器阻力系數(shù)；m1是車輪質(zhì)量，z1是車輪離開平衡點的位移；K是懸掛剛度，Kt是車輪剛度，q是輸入的路面不平度函數(shù)。式（1）、式（2）分別為車身和車輪的振動微分方程[1]。

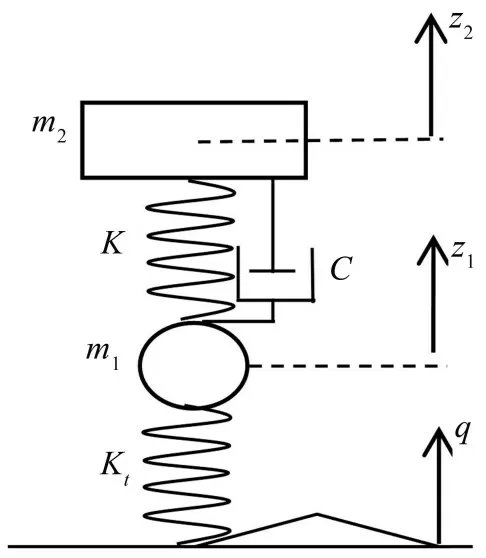
圖1 車輛二自由度振動模型示意圖

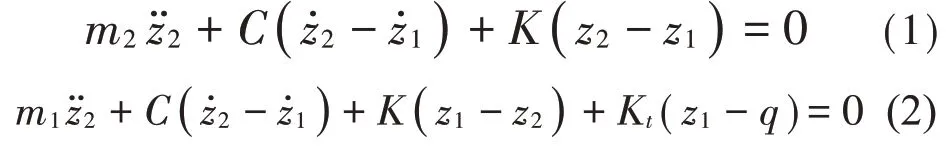
ω0=,相當(dāng)于m1不動時，m2無阻尼自由振動的固有頻率；ωt=,相當(dāng)m2不動，m1無阻尼自由振動的固有頻率；

該系統(tǒng)的簡正模頻率為：

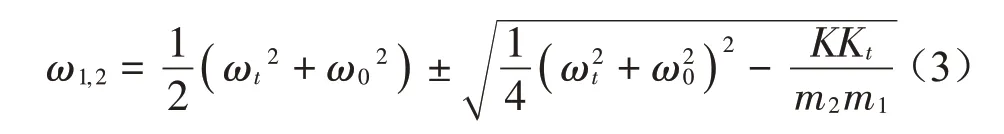
當(dāng)剛度比γ==9、質(zhì)量比μ==10 時，ω1=0.95ω0,ω2≈ωt=10ω0。

可以得出，在頻率ω1附近的振動主要是車身振動；在頻率為ω2附近的振動主要是車輪振動[1]。

在簡諧振動q=q0cos(ωt)的策動作用下，令λ=ω/ω0，得到車身位移頻率響應(yīng)函數(shù)H2(ω)=|H2(ω) |cos(ωt+θ2)的穩(wěn)態(tài)解和車輪位移頻率響應(yīng)函數(shù)H1(ω)=|H1(ω) |cos(ωt+θ1)穩(wěn)態(tài)解，對應(yīng)的加速度頻率響應(yīng)函數(shù)分別為-ω2H2(ω) 和-ω2H1(ω)。|H2(ω) |、tgθ2、|H1(ω) |、tgθ1的解析式如式（4）、式（5）、式（6）、式（7）所 示，其 中ξ=。

在ω0=2 π/s、ξ=0.25 時，車身和車輪的位移與加速度頻率響應(yīng)函數(shù)曲線分別如圖2、圖3所示。

從圖2 中可以看出，車身位移振幅在車身共振頻率ω0附近有極大值，在車輪共振頻率ωt附近略有升高；車身加速度振幅在車輪共振頻率ωt附近有極大值。從圖3 中可以看出，在策動頻率小于車輪共振頻率ωt時，車輪位移振幅與q的幅值接近，在車輪共振頻率ωt附近有極大值，之后車輪位移振幅逐漸降低；在策動頻率小于車輪共振頻率ωt時，車輪加速度振幅由小到大逐漸上升，在車輪共振頻率ωt附近達(dá)到極大值，之后有所下降并趨于平緩。

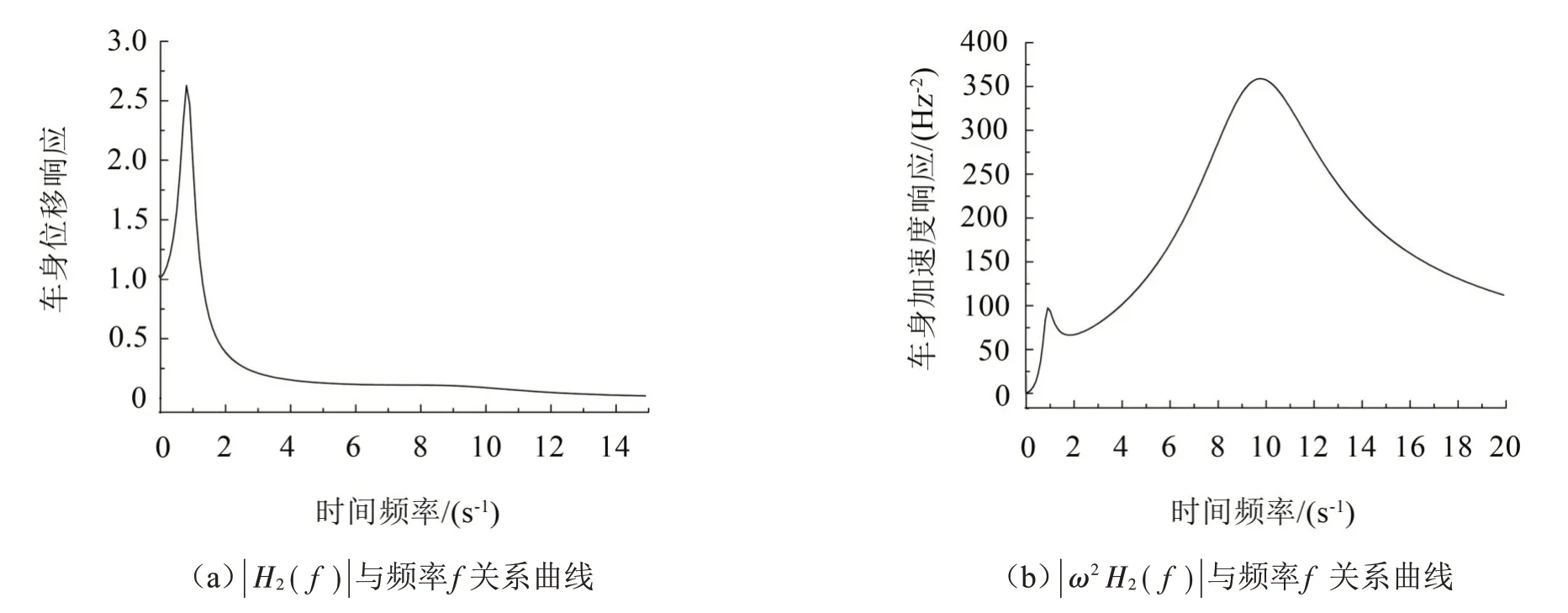
圖2 車身位移和加速度頻響曲線

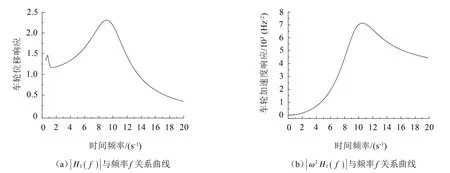
圖3 車輪位移和加速度頻響曲線

2 減速帶形狀的空間頻譜分析

減速帶橫截面的輪廓線一般為近三角形曲線、圓弧形曲線、升余弦形曲線等，令減速帶橫截面高h(yuǎn)=0.05 m，寬b=0.3 m，如圖4 所示；式（8）、式（9）、式（10）分別為對應(yīng)的圓弧形曲線、升余弦形曲線、三角形曲線的解析表達(dá)式，x的單位是m。

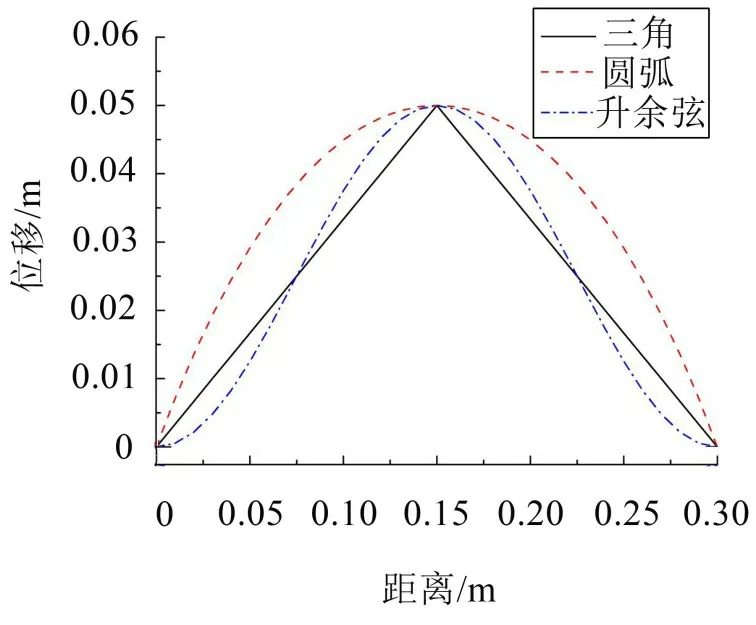
圖4 三角形、升余弦形和圓弧形曲線

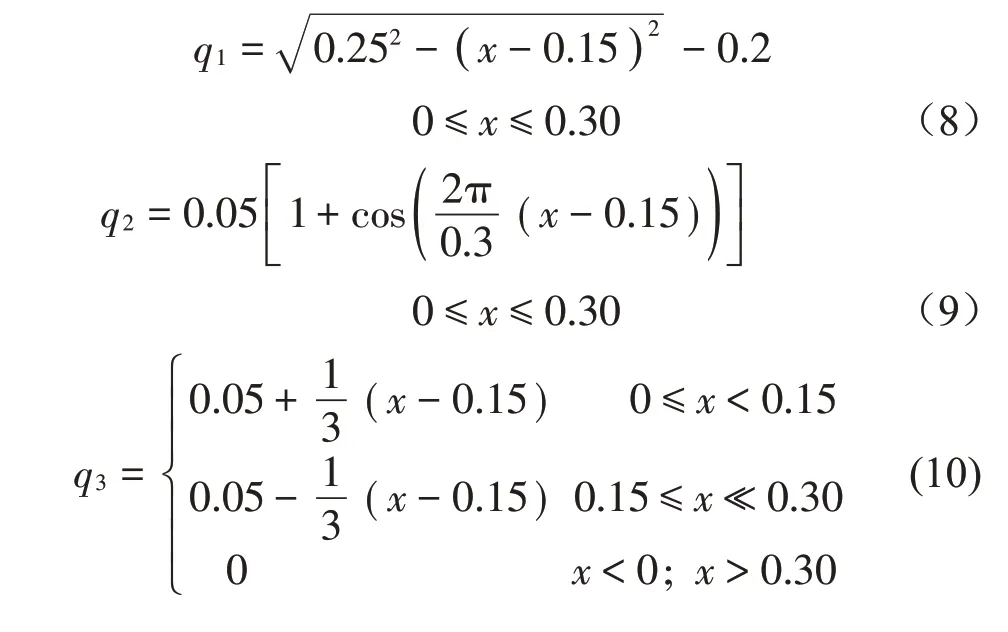
從頻譜分析角度研究減速帶對通過車輛振動的影響。升余弦形曲線和三角形曲線的傅里葉變換空間頻譜有解析式，分別為式（11）、式（12），從式（12）可以得出：若減速帶寬度b減小，頻帶寬度增加（低頻成分減少，高頻成分增加）；也可通過數(shù)值積分求得圓弧形曲線空間頻譜曲線。3種曲線的空間頻譜曲線如圖5 所示（只畫出正半軸的頻譜，n為空間頻率），可得三角形曲線、圓弧形曲線、升余弦形曲線的空間頻譜的第一個零點分別約為6.7/m、4.7/m、6.6/m。

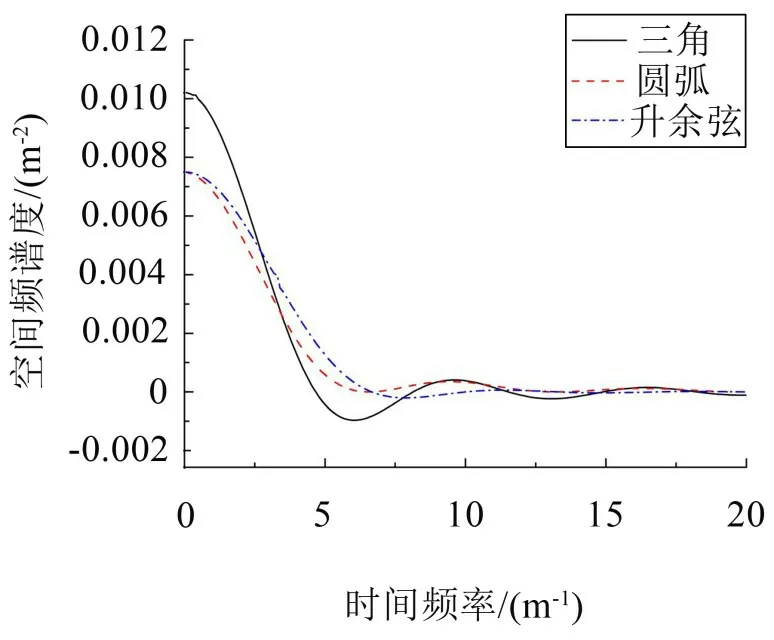
圖5 三角形、升余弦形和圓弧形曲線的空間譜

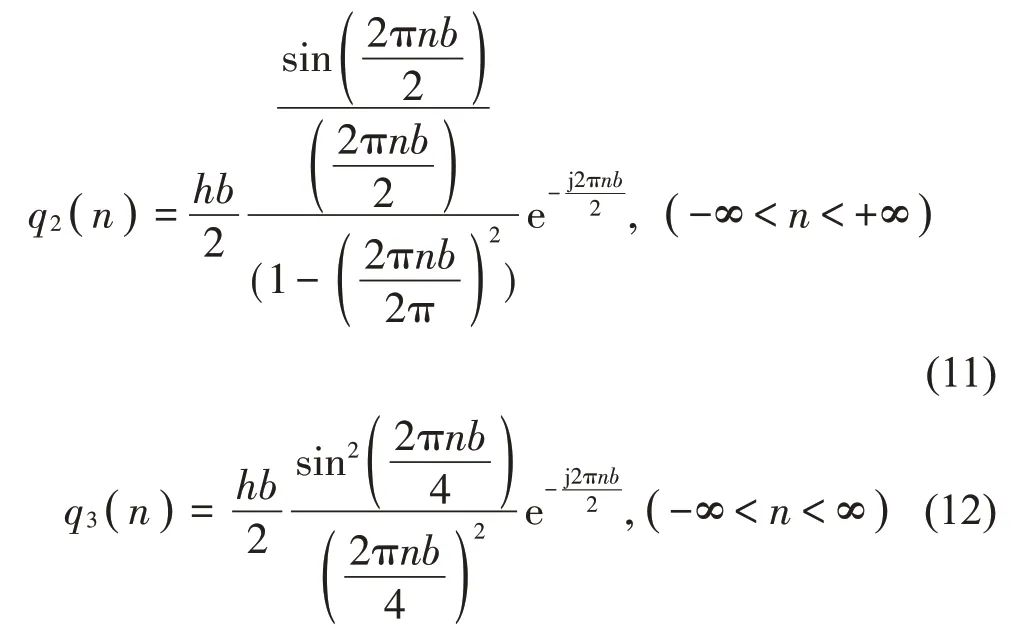
3 車身和車輪的位移與加速度瞬態(tài)解

不考慮圓形車輪與減速帶接觸過程中水平方向車速的變化（V=Vx=常數(shù)），認(rèn)為X=Vt，即nV=f,X為車輛行駛距離，f為時間頻率。三角形減速帶對通過車輛作用的時間頻譜公式可由三角形減速帶的空間頻譜公式（12）得出：

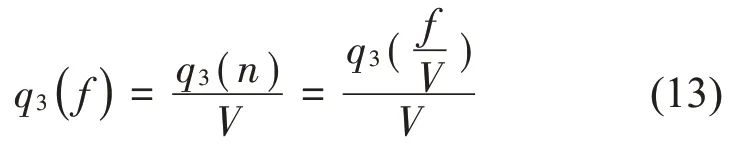
車速增大，相當(dāng)時間頻譜寬度增加（低頻成分減少，高頻成分增多）。在車速為1 m/s～17 m/s時，將三角形減速帶的時間頻譜q3(f)分別和車身位移響應(yīng)函數(shù)H2(f)、車輪位移響應(yīng)函數(shù)H1(f)相乘，再進行逆傅里葉變換（取實部數(shù)值積分），可以得到不同車速下車身和車輪的位移與時間關(guān)系的瞬態(tài)解，見式（14）；其中式（14）中θ分別取θ1和θ2；H(ω)分別取H1(f)和H2(f)。用同樣的方法也可得到車身和車輪的加速度與時間關(guān)系的瞬態(tài)解。當(dāng)車輛通過減速帶的車速為3 m/s、5 m/s、10 m/s時，可得車身和車輪的位移與時間關(guān)系曲線，如圖6所示；車身和車輪的加速度與時間關(guān)系曲線，如圖7所示。

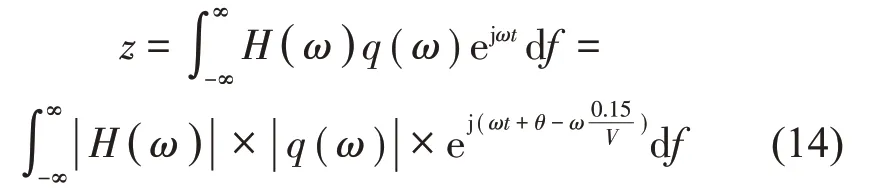
4 討論

通過車身和車輪的位移、加速度與時間關(guān)系曲線，本文分別從作用時間段（車輛通過減速帶時間）和作用之后時間段兩部分來分析車輛振動位移和加速度的響應(yīng)，將不同車速下作用時間內(nèi)的第一正向峰值進行比較[8]，將不同車速下作用時間之后第一個正向峰值進行比較。

當(dāng)車速為1 m/s、3 m/s、5 m/s、10 m/s 時，車輛通過三角形減速帶（b=0.3 m）的對應(yīng)時間（作用時間）分別為0.3 s、0.1 s、0.06 s、0.03 s。車身和車輪的位移、加速度在作用時間之后，將按有阻尼自由振動規(guī)律衰減，衰減振動中均包括車身單獨自由衰減振動的成分和車輪單獨自由衰減振動的成分，隨車速不同，其對車身和車輪的影響大小不同。從圖6（a）可以得出，車身單獨自由衰減振動準(zhǔn)周期約為1.07 s，從圖7（b）可以得出，車輪單獨自由衰減振動準(zhǔn)周期約為0.1 s。

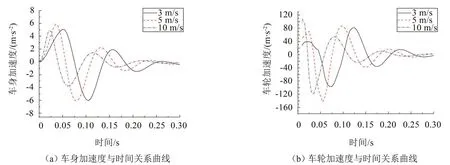
圖7 車身和車輪的加速度與時間關(guān)系曲線

4.1 車身和車輪的位移隨車速變化

（1）車身位移：如圖6（a）所示，作用時間內(nèi)車身位移第一個正向峰值隨車速增大而下降，說明隨車速增大，車身減震器壓縮量加大。

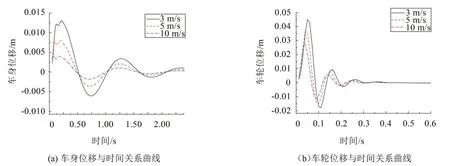
圖6 車身和車輪的位移與時間關(guān)系曲線

（2）車輪位移：如圖6（b）和圖8 所示，車速在4 m/s以下時，作用時間內(nèi)的車輪位移第一正向峰值在0.05 m（減速帶的高度h=0.05 m）附近，之后隨車速增大而下降，說明隨車速增大，輪胎壓縮量加大。

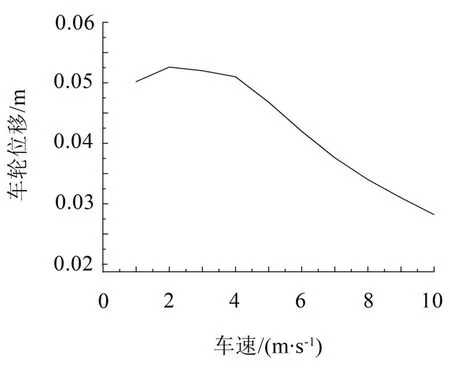
圖8 車輪位移與車速關(guān)系曲線

4.2 車身和車輪的加速度隨車速變化

（1）車身加速度：如圖7（a）和圖9 所示，在作用時間內(nèi)，車速在1 m/s～4 m/s時，車身加速度第一正向峰值隨車速增大而增大；車速約在5 m/s 以上時，車身加速度第一正向峰值隨車速增大而降低[9]。車身加速度出現(xiàn)極大值與車身加速度頻率響應(yīng)函數(shù)在ωt附近有極大值有關(guān)，見圖2（b）。

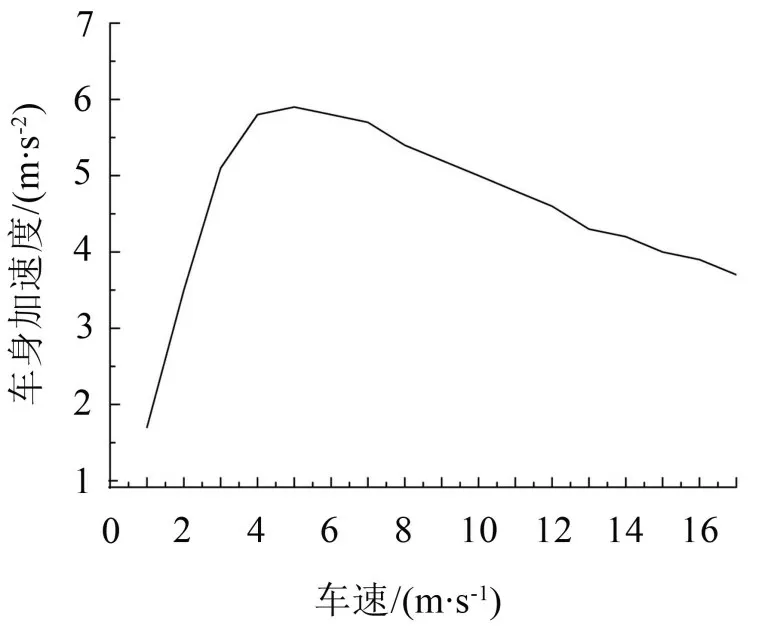
圖9 車身加速度與車速關(guān)系曲線

（2）車輪加速度：如圖7（b）和圖10所示，車輪受到兩次較大正向沖擊。在作用時間內(nèi)，車速在1 m/s～17 m/s 之間時，車輪加速度第一正向峰值隨車速增大而升高；在作用時間之后，車速在1 m/s～4 m/s內(nèi)時，車輪加速度第一正向峰值隨車速增大而升高，車速約在5 m/s以上時，車輪加速度第一正向峰值隨車速增大而下降。

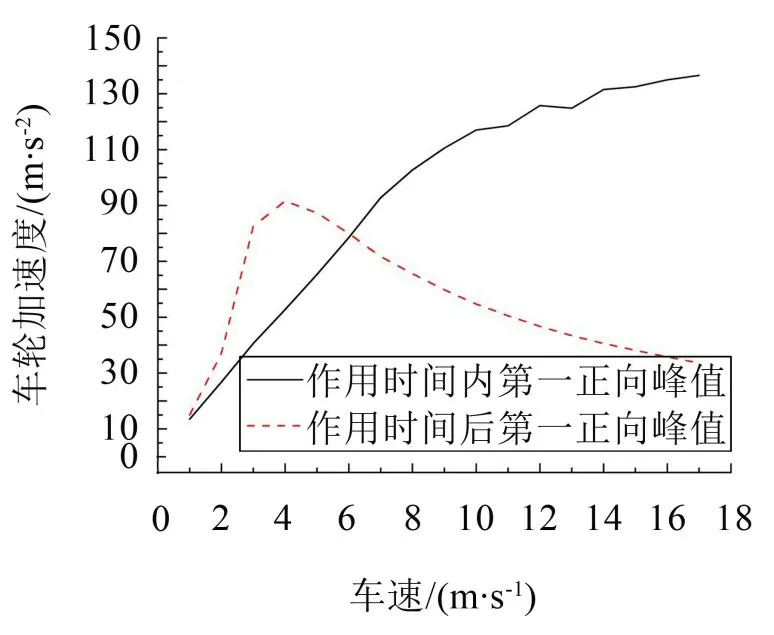
圖10 車輪加速度與車速關(guān)系曲線

比較圖7（a）和圖7（b）可以看出，在作用時間之后車輪加速度第一正向峰值出現(xiàn)時刻，恰是車身加速度由第一負(fù)向峰值回到零點附近的時刻。所以，在作用時間之后車輪加速度第一正向峰值與車速關(guān)系曲線，與作用時間內(nèi)車身加速度與車速關(guān)系曲線相似，這是車身與車輪耦合作用的結(jié)果，使車輪加速度在作用時間后的第一正向峰值也較大。

車輪的振動加速度比車身的振動加速度大許多倍，這與車身和車輪的質(zhì)量比有關(guān)。

4.3 減速帶寬度對車身振動加速度的影響

以三角形減速帶為例，取高h(yuǎn)為0.05 m，寬b分別為0.30 m、0.40 m、0.50 m等3種情況，得出車身加速度與車速關(guān)系曲線，如圖11所示。減速帶寬度增加，車身加速度最大值不變，但向車速大的方向移動。利用這一點，想要從某一速度開始限制車速時，在高度不變情況下，可適當(dāng)改變減速帶的寬度[10－11]。

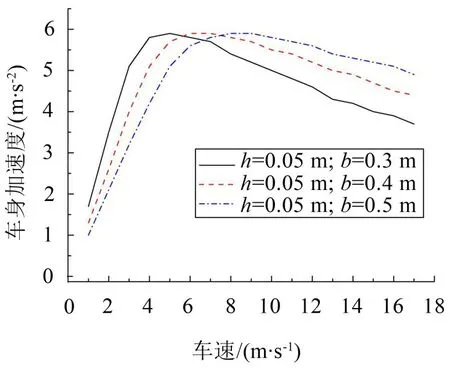
圖11 3種寬度減速帶下的車身加速度與車速關(guān)系曲線

4.4 3種減速帶對車輛振動情況的比較

從碰頭加速度（t=0時的加速度）、加速度與時間關(guān)系曲線形狀和作用時間內(nèi)正向峰值等3方面對車輛振動加速度進行比較，車速在1 m/s附近和車速約在3 m/s以上分別為兩種典型情況。

（1）車身加速度：如圖12 所示，3 種形狀減速帶對車身的振動效果比較接近。車速在1 m/s附近時，圓弧形減速帶引起車身的碰頭加速度較大；隨車速增大（1 m/s～5 m/s），車身的碰頭加速度差異減小,曲線形狀比較圓滑，正向峰值接近；車速約在5 m/s以上時，圓弧形減速帶引起車身的振動效果較大一些，如圖13所示。

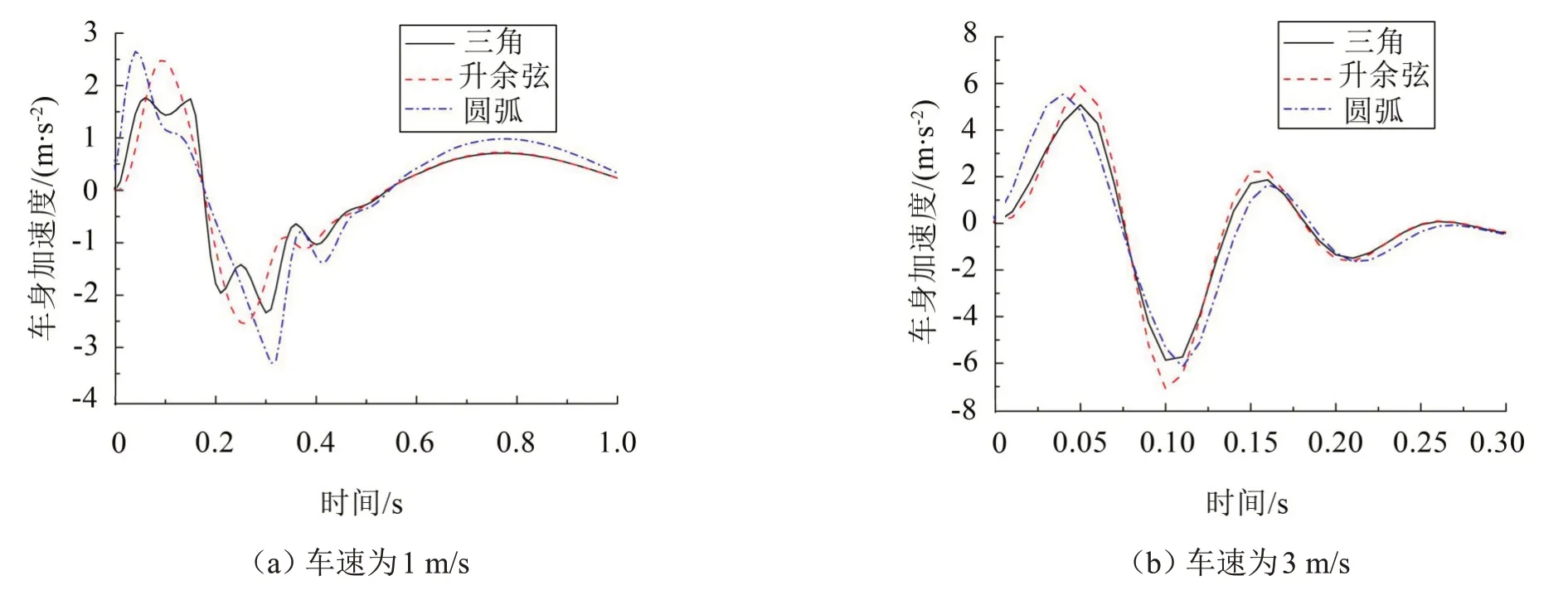
圖12 車身加速度與時間關(guān)系曲線

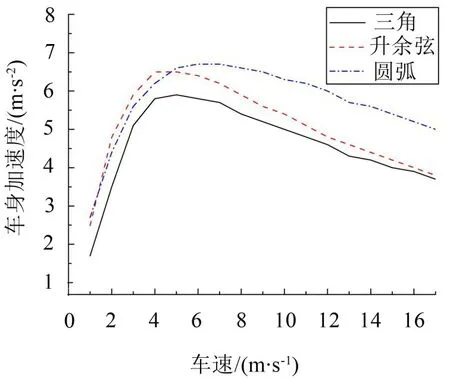
圖13 3種減速帶下車身加速度與車速關(guān)系曲線

（2）車輪加速度：如圖14 所示，3 種形狀的減速帶對車輪的振動效果主要表現(xiàn)在圓弧形減速帶引起車輪的碰頭加速度較大。車速在1 m/s附近時，圓弧形減速帶引起車輪的加速度正向峰值相對較大；車速約在5 m/s以上時，圓弧形減速帶引起車輪的加速度在作用時間之后第一正向峰值較大一些，如圖15所示，與圖13 所示的結(jié)果相同；升余弦形減速帶引起車輪的碰頭加速度較小，振動曲線比較圓滑。

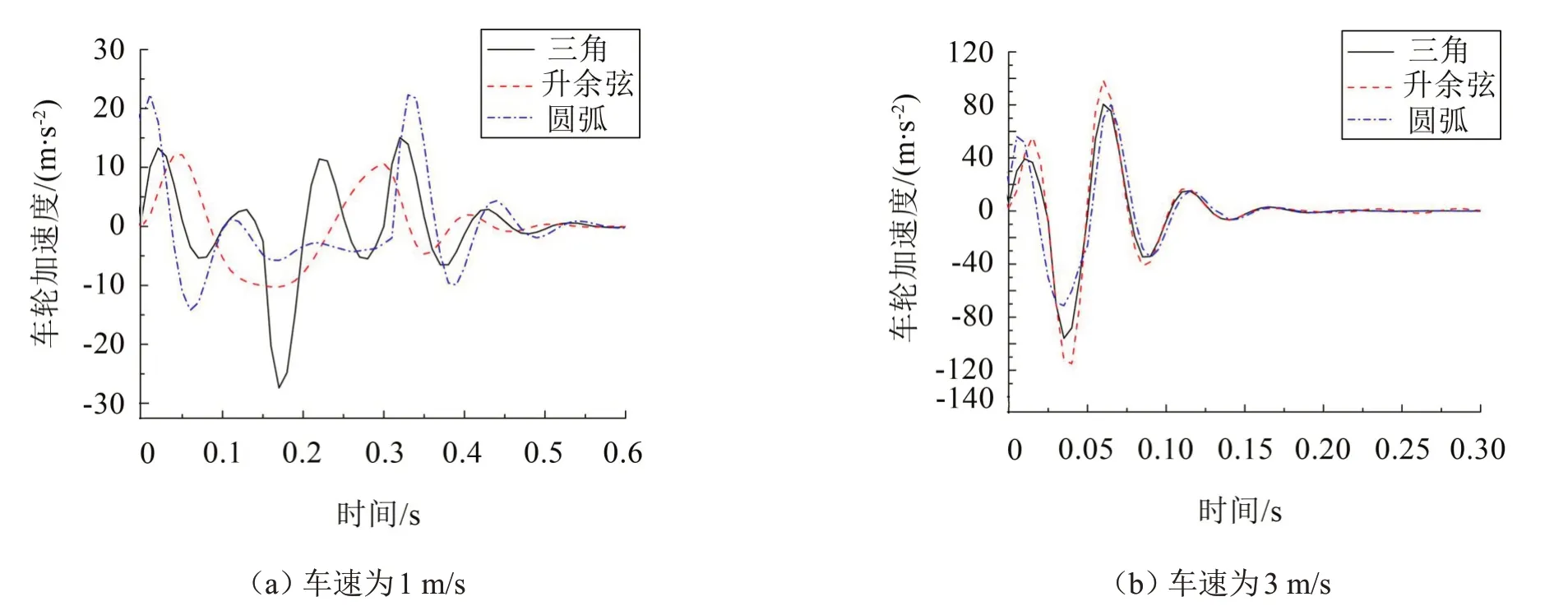
圖14 車輪加速度與時間關(guān)系曲線

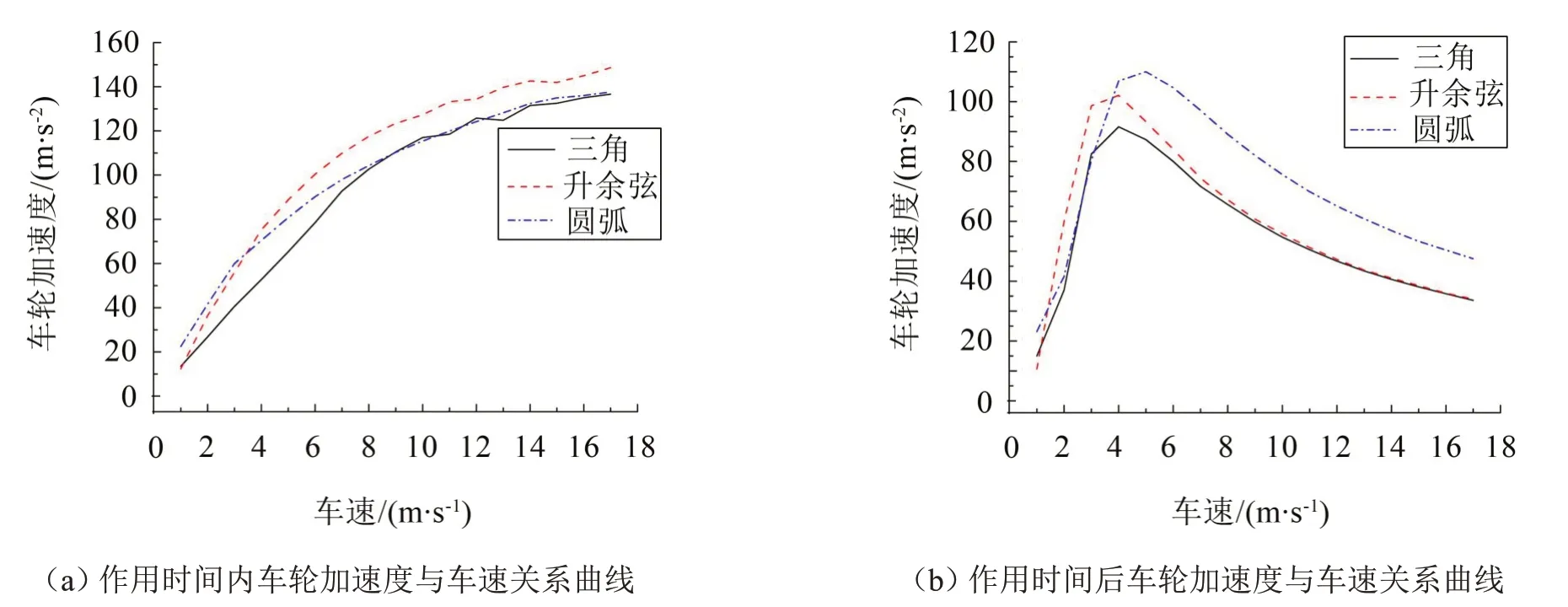
圖15 3種減速帶下車輪加速度與車速關(guān)系曲線

5 結(jié)語

(1)在文獻(xiàn)[1]中的車輛振動系統(tǒng)的二自由度模型和有關(guān)參數(shù)基礎(chǔ)上，分析了3 種形狀的減速帶對車輛不同車速下振動的影響。減速帶的寬度減小，其空間頻譜頻帶變寬；車速增大，減速帶對車輛作用的時間頻譜高頻成分增加。

(2）對于車身振動加速度而言，隨著車速的增大，作用時間內(nèi)車身加速度第一正向峰值和作用時間后車身加速度第一正向峰值由小到大上升，到達(dá)一定車速后又開始下降。出現(xiàn)極大值是因為車身加速度頻率響應(yīng)函數(shù)在車輪共振頻率附近有極大值。

(3）對于車輪振動加速度而言，車輪經(jīng)歷兩次較大正向沖擊。在作用時間內(nèi)，當(dāng)車速在1 m/s～17 m/s 范圍內(nèi)時車輪加速度第一正向峰值隨車速增大而增大；在作用時間之后，車輪加速度第一正向峰值由小到大上升，到達(dá)一定車速后又開始下降。

(4）3 種形狀減速帶對車身加速度的影響比較接近，對車輪加速度的影響有一定差異。圓弧形減速帶引起的車輪碰頭加速度較大，車速約在5 m/s以上時，圓弧形減速帶引起的車輪加速度在作用時間之后第一正向峰值較大；升余弦形減速帶引起的碰頭加速度較小，振動曲線比較圓滑。