基于振動(dòng)分析的壓型鋼板-混凝土組合樓板等效計(jì)算模型研究

盧華喜，劉美豪，方 超，吳必濤，梁平英

（1.華東交通大學(xué) 土木建筑學(xué)院，南昌 330013；2.華東交通大學(xué) 軌道交通基礎(chǔ)設(shè)施性能監(jiān)測與保障國家重點(diǎn)實(shí)驗(yàn)室，南昌 330013；3.江西省交通投資集團(tuán)有限責(zé)任公司，南昌 330025）

閉口型壓型鋼板-混凝土組合樓板（簡稱“組合樓板”）因具有整體性好、節(jié)省模板和工業(yè)化程度高等優(yōu)點(diǎn)在鋼結(jié)構(gòu)建筑中的應(yīng)用越來越多。同時(shí)因其受力性能優(yōu)越、結(jié)構(gòu)較輕柔的特點(diǎn)多被用于大跨度樓蓋體系，在反復(fù)變化的環(huán)境振動(dòng)中特別是人行荷載作用下，易產(chǎn)生環(huán)境振動(dòng)超標(biāo)或振動(dòng)舒適度問題。

目前樓板體系的振動(dòng)問題受到了國內(nèi)外學(xué)者們的廣泛關(guān)注，特別是針對大跨度樓蓋的振動(dòng)問題，國內(nèi)外學(xué)者進(jìn)行了大量的研究。Varela 等[1]通過試驗(yàn)研究了組合樓板的人致振動(dòng)問題，分析了人行軌跡、隨機(jī)性和人數(shù)等因素對振動(dòng)的影響。Sanayei等[2]建立基于阻抗的解析模型，并結(jié)合模型試驗(yàn)，發(fā)現(xiàn)增加較低層樓板的厚度能有效抑制振動(dòng)向上部傳播。陳曦[3]通過實(shí)測和有限元分析發(fā)現(xiàn)地鐵振動(dòng)所致裝配式框架結(jié)構(gòu)樓面的振動(dòng)以豎向振動(dòng)為主，且豎向振動(dòng)加速度隨樓層的增加逐漸增大。張坤等[4]通過人致激勵(lì)試驗(yàn)對中科院巨型鋼框架懸掛結(jié)構(gòu)體系組合樓板開展了舒適度評(píng)價(jià)。

組合樓板的結(jié)構(gòu)形式相對復(fù)雜，且在模型建立時(shí)需要考慮鋼板與混凝土的共同作用，在進(jìn)行組合樓板體系的振動(dòng)問題分析時(shí)，通常需要建立多層梁-柱-樓板結(jié)構(gòu)的數(shù)值模型，樓板部分如采用實(shí)體模型，則建模工作量巨大，且需要耗費(fèi)難以估量的計(jì)算時(shí)間，給建模分析帶來困難，因此建立組合樓板等效簡化計(jì)算模型尤為重要。盧華喜等[5]在研究中采用殼單元等厚度的原則模擬實(shí)體樓板。Silva等[6]在研究中采用厚度僅為75 mm的殼單元對肋高75 mm板厚150 mm 的開口型壓型鋼板-組合樓板進(jìn)行模擬。李永梅等[7]將殼單元分成壓型鋼板層、混凝土板層和鋼筋層進(jìn)行建模，分析了組合樓板對鋼框架結(jié)構(gòu)抗震性能的影響。本文對于閉口型壓型鋼板-混凝土組合樓板的振動(dòng)問題，以位移等效和剛度等效為原則，分別建立了組合樓板的各向同性等效計(jì)算模型和正交異性等效計(jì)算模型，并通過有限元模擬和樓板振動(dòng)試驗(yàn)進(jìn)行了比較分析，驗(yàn)證了等效計(jì)算模型的可靠性和計(jì)算的高效性，為大跨度組合樓板體系振動(dòng)問題的有限元建模提供參考。

1 組合樓板的等效計(jì)算模型

1.1 各向同性等效計(jì)算

撓度相等原則為在相同荷載條件下組合樓板的三維實(shí)體模型中心最大撓度ωmax1和各向同性等效模型中心最大撓度ωmax2相等。具體等效過程如下：

(1) 建立組合樓板的三維實(shí)體模型，利用ANSYS 有限元軟件計(jì)算四邊簡支條件下組合樓板在豎向均布荷載下的最大撓度ωmax1。

(2)由薄板理論可知，承受豎向均布荷載的四邊簡支各向同性板的最大撓度為[8]：

其中：D=，D為各向同性板的等效剛度；q0為豎向均布荷載；b為板的短邊尺寸；h為板厚，m=1,3,5,…,n=1,3,5,…；α為撓度系數(shù)，取決于板的長寬比a/b。

對于不同長寬比的矩形板，撓度系數(shù)α的取值見表1。

表1 不同長寬比的撓度系數(shù)取值

(3) 令ωmax1=ωmax2，可得出各向同性板的等效彎曲剛度D和各向同性等效板的厚度h；各向同性等效板的跨度和寬度與原組合樓板一致；等效板的密度可以根據(jù)等效板的質(zhì)量與原組合樓板的質(zhì)量相等來確定；各向同性等效板的泊松比和彈性模量取為原組合樓板混凝土材料的泊松比和彈性模量。

1.2 正交異性等效計(jì)算

在有限元分析軟件中將組合樓板等效為正交異性板進(jìn)行建模分析時(shí)，需要定義x、y軸的彈性模量Ex、Ey，x、y方向的泊松比vxz、vyz和等效剪切模量Giso等參數(shù)，計(jì)算時(shí)取垂直于順肋方向（板寬方向）為x方向，順肋方向（板長方向）為y方向。進(jìn)行有限元求解時(shí)，總剛度矩陣D作為整體出現(xiàn)在計(jì)算過程中，只要D的總量不變，最終的求解結(jié)果也不變[9]。總剛度矩陣D的大小主要由彈性模量E和慣性矩I的乘積決定，基于等剛度的原則可以令EIx=ExI、EIy=EyI的方式將正交異性板x、y方向的慣性矩之比轉(zhuǎn)換為彈性模量之比，即Ex=。

根據(jù)文獻(xiàn)[9]中方法，正交異性等效板x方向的泊松比νxz=ν（ν為混凝土的泊松比）；y方向的泊松比為νyz=。令Ey=Ec，Ec為混凝土的彈性模量，因此只要求出正交異性等效平板x、y兩個(gè)方向的慣性矩Ix、Iy，即可得到正交異性等效板兩個(gè)方向的彈性模量和泊松比。

正交異性等效板剪切模量G可按式（3）[10]計(jì)算。

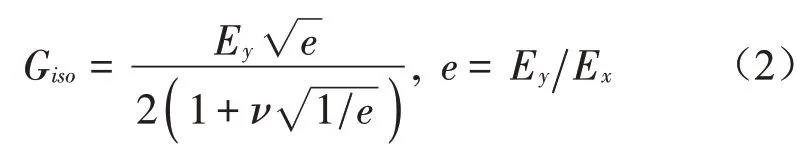
設(shè)等效的正交異性平板厚度為tz，則有Iy=（1.0為單位長度），可在求得Iy后確定tz。

正交異性等效板的密度ρe可通過原組合樓板與正交異性等效板質(zhì)量相等的原則計(jì)算。

基于以上等效原則，結(jié)合以下某尺寸的單塊組合樓板進(jìn)行正交異性等效計(jì)算。其截面構(gòu)造圖如圖1至圖2所示。計(jì)算時(shí)取x、y方向上的單位長度a為1.0 m。等效過程如下：

1)計(jì)算正交異性等效板x方向截面的慣性矩Ix。

組合樓板沿x方向平行于xz的截面由混凝土和底部的鋼板組成，如圖1至圖2所示。可先計(jì)算混凝土部分和鋼板部分的截面慣性矩，再計(jì)算組合截面整體的截面慣性矩Ix。先按長度為L的截面計(jì)算，再將結(jié)果按單位長度1 m轉(zhuǎn)化。計(jì)算過程如下：

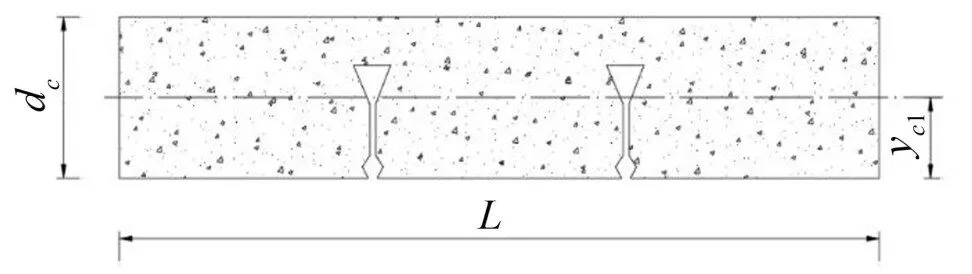
圖1 x方向混凝土部分橫截面

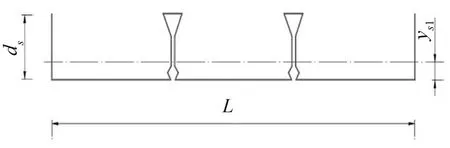
圖2 x方向壓型鋼板橫截面

（1）基于CAD制圖等軟件易計(jì)算混凝土部分和壓型鋼板部分單位長度的截面面積Ac、As和中性軸的位置yc1、ys1及單位長度的慣性矩Ic、Is。

（2）混凝土與鋼板組合截面的面積Ax、中性軸位置、慣性矩Ix分別按以下公式計(jì)算：

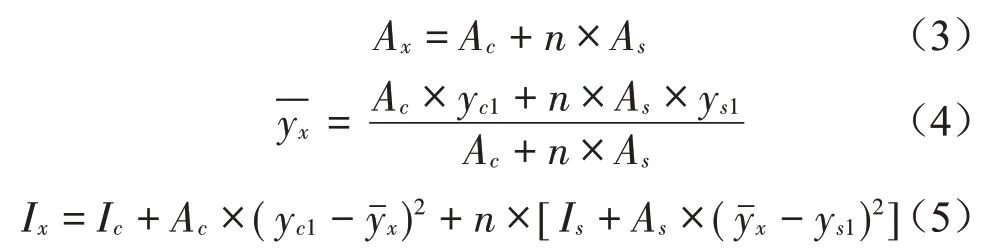
式中，n=Es/Ec，Es為底部鋼板的彈性模量，Ec為混凝土的彈性模量。

2)計(jì)算正交異性等效板y方向截面的慣性矩Iy。

由于異形凸肋的存在，組合樓板平行于y方向（長邊）截面有d1和d2兩個(gè)高度的截面，故沿y方向的正交異性等效截面慣性矩Iy無法直接求出。可將樓板考慮為承受均布荷載qy的簡支梁，沿x方向（跨度為L）考慮取L為簡支梁的跨度，沿y方向取1 m（單位長度）為簡支梁的寬度，簡支梁剖面圖如圖3所示。為便于分析，將簡支梁中間的異形凸肋簡化成矩形，簡化后的剖面圖如圖4所示。

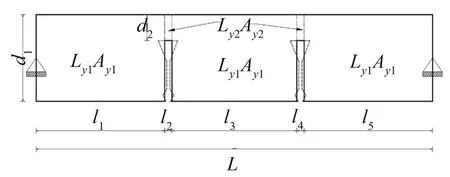
圖3 簡支梁剖面

采用ANSYS 軟件中的BEAM3 梁單元建立如圖4 所示的簡支梁模型，采用定義單元實(shí)常數(shù)的方

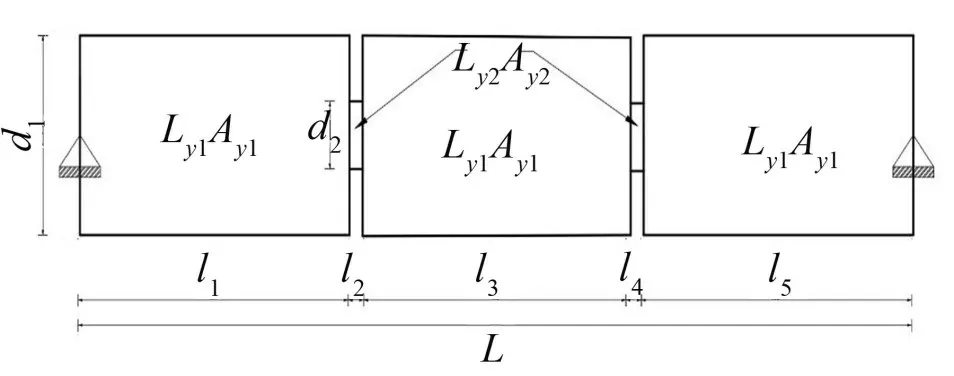
圖4 簡支梁的簡化

式分別將高度為d1和d2截面的橫截面積和慣性矩賦予對應(yīng)部分的BEAM3梁單元。施加均布荷載qy，求解出簡支梁的最大撓度Δmax1，Δmax1即為簡支組合樓板在均布荷載下沿x方向的撓度。

由材料力學(xué)易知，簡支梁在均布荷載作用下跨中撓度為：

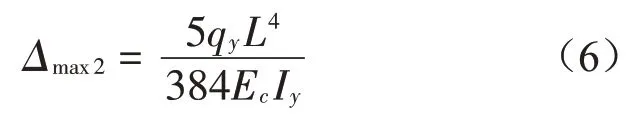
令Δmax1=Δmax2，可求得組合樓板沿順肋方向即正交異性等效板y方向的慣性矩Iy。

組合樓板高度為d1和d2截面的截面積和慣性矩的計(jì)算如下，兩個(gè)截面的示意圖如圖5所示。

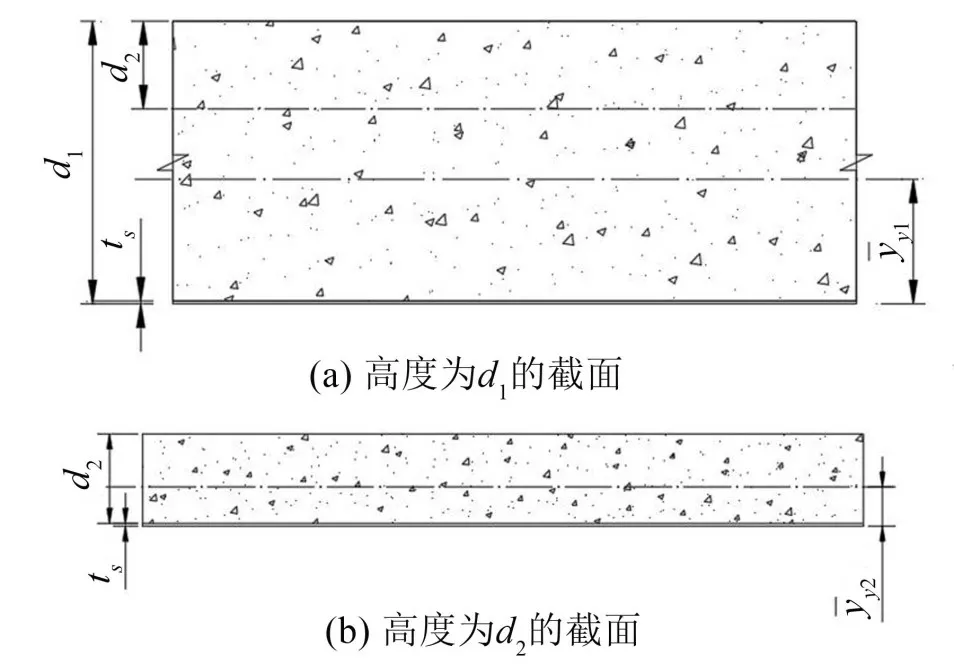
圖5 y方向不同高度橫截面圖（單位：mm）

（1）高度為d1的截面面積、中和軸位置和截面慣性矩的計(jì)算如下：

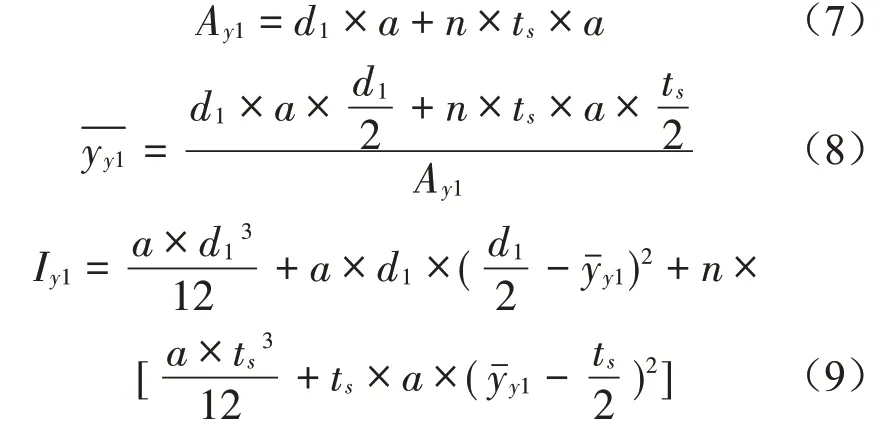
（2）高度為d2的截面面積、中和軸位置和截面慣性矩的計(jì)算如下：

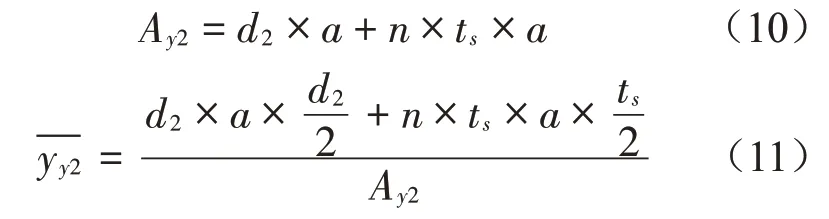
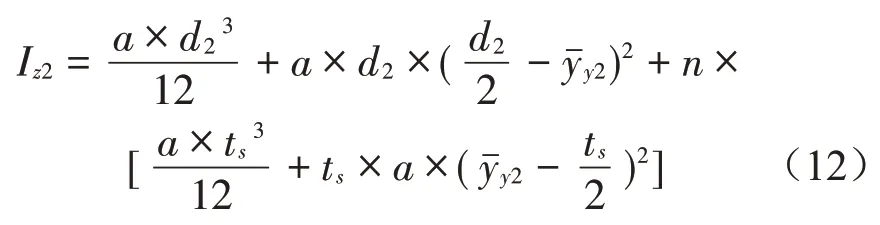
3)正交異性等效板的厚度tz和x、y方向的彈性模量Ex、Ey、泊松比vxz、vyz及剪切模量Giso均可在已知Ix、Iy條件下，由上文中的等效原則計(jì)算。

2 組合樓板振動(dòng)試驗(yàn)

2.1 試件設(shè)計(jì)

本次試驗(yàn)中根據(jù)相關(guān)規(guī)程、規(guī)范和圖集，制作了兩塊組合樓板試件，試件尺寸參數(shù)見表2。由于組合樓板底部采用了閉口型熱鍍鋅壓型鋼板，且作為單向板不用考慮混凝土的收縮變形，故組合樓板中未配置分布鋼筋。

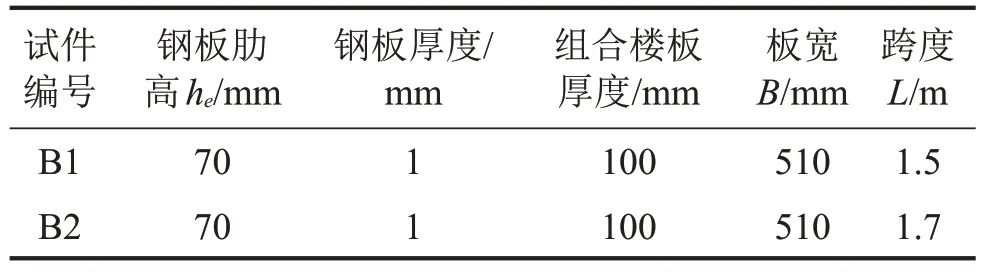
表2 組合樓板試件參數(shù)

組合樓板的橫截面示意圖如圖6所示。

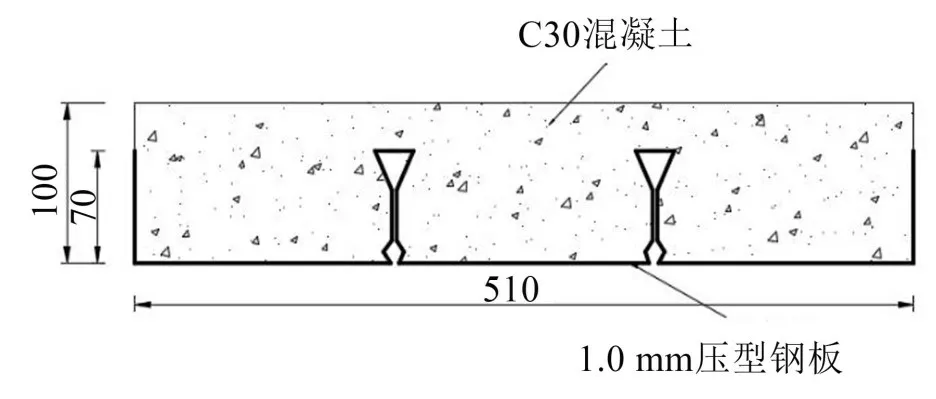
圖6 組合樓板橫截面（單位：mm）

2.2 試驗(yàn)方案

（1）模態(tài)分析試驗(yàn)

進(jìn)行模態(tài)分析試驗(yàn)時(shí)，組合樓板邊界條件為兩邊簡支，在板面上布置4 個(gè)加速度傳感器以拾取樓板的振動(dòng)加速度，加速度傳感器布置圖如圖7所示。利用激勵(lì)錘在組合板上錘擊，使樓板進(jìn)行衰減振動(dòng)，對每塊試件進(jìn)行3次獨(dú)立的錘擊。

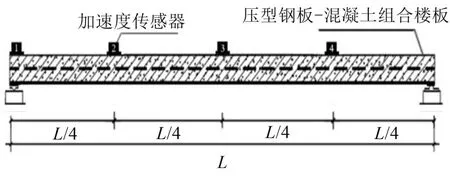
圖7 模態(tài)分析試驗(yàn)中傳感器布置

模態(tài)分析試驗(yàn)的現(xiàn)場實(shí)驗(yàn)圖如圖8所示。

圖8 模態(tài)分析試驗(yàn)

（2）樓板的激振試驗(yàn)

實(shí)驗(yàn)時(shí)使用電動(dòng)式激振器使組合樓板產(chǎn)生受迫振動(dòng)，由于環(huán)境振動(dòng)大多屬于微振范疇，故激振試驗(yàn)采用的激振力大小分別為4 N、8 N、12 N、16 N、20 N，激振頻率分別為5 HZ、10 HZ、15 HZ、20 Hz。激振試驗(yàn)中采用正弦波激振，采用加速度傳感器采集樓板振動(dòng)的加速度信號(hào)，激振試驗(yàn)示意圖見圖9。

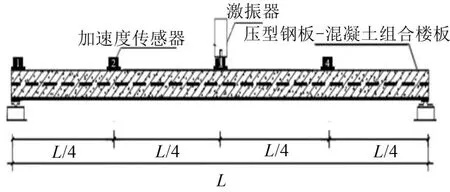
圖9 激振試驗(yàn)

2.3 試驗(yàn)結(jié)果

（1）模態(tài)試驗(yàn)結(jié)果

測得兩塊組合樓板的基頻和阻尼比如表3所示。

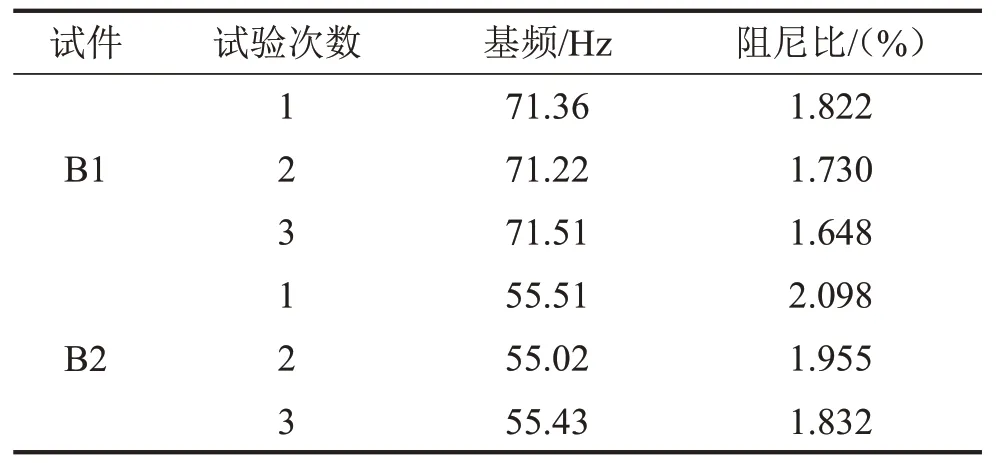
表3 組合樓板的基頻和阻尼比

（2）激振試驗(yàn)結(jié)果

兩塊組合樓板跨中（傳感器3）峰值加速度隨激振頻率和激振幅值的變化情況見表4。

從表4 中可以看出，在小幅值的簡諧荷載持續(xù)作用下，組合樓板的加速度峰值與激振幅值幾乎呈線性關(guān)系；隨著波形頻率的增大，簡諧激振響應(yīng)加速度的增大幅度越大，且在相同激振幅值下，B2 板的加速度峰值相較于B1板平均增加了25%，可見樓板跨度增加對其在動(dòng)力作用下振動(dòng)加速度的影響顯著。

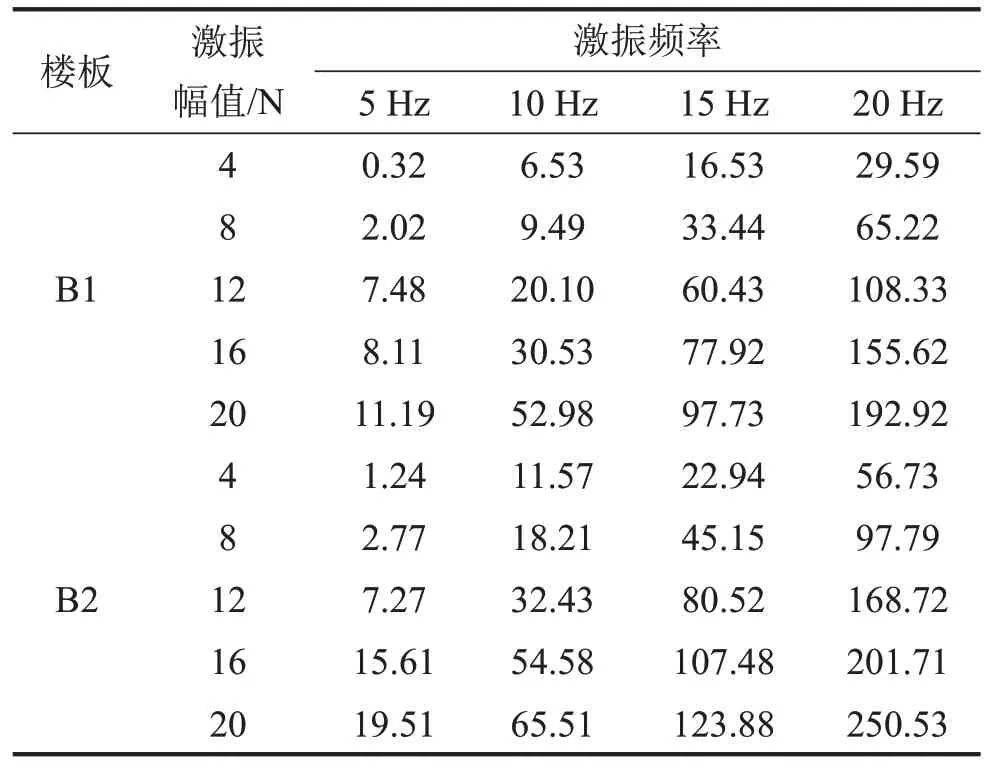
表4 組合板激振加速度峰值/(mm?s-2）

3 對比分析

3.1 計(jì)算模型的建立

利用ANSYSY 有限元軟件建立兩塊試件的三維實(shí)體模型、各向同性等效模型和正交異性等效模型，并模擬樓板的邊界條件和激勵(lì)方式。三維實(shí)體模型按照樓板材料的實(shí)測屬性建立，各向同性和正交異性等效模型根據(jù)本文給出的等效原則建立。

建立三維實(shí)體模型時(shí)，混凝土板采用solid65 三維實(shí)體單元模擬，壓型鋼板采用shell181 薄殼單元模擬，采用共享節(jié)點(diǎn)的方式模擬壓型鋼板和混凝土之間的共同受力。表5 為三維實(shí)體模型的材料屬性，壓型鋼板和混凝土的材料屬性取自實(shí)驗(yàn)結(jié)果。各向同性等效模型和正交異性等效模型均采用shell181薄殼單元模擬，等效前后組合樓板的材料屬性和尺寸參數(shù)見表6～表7。

表5 組合樓板的材料屬性

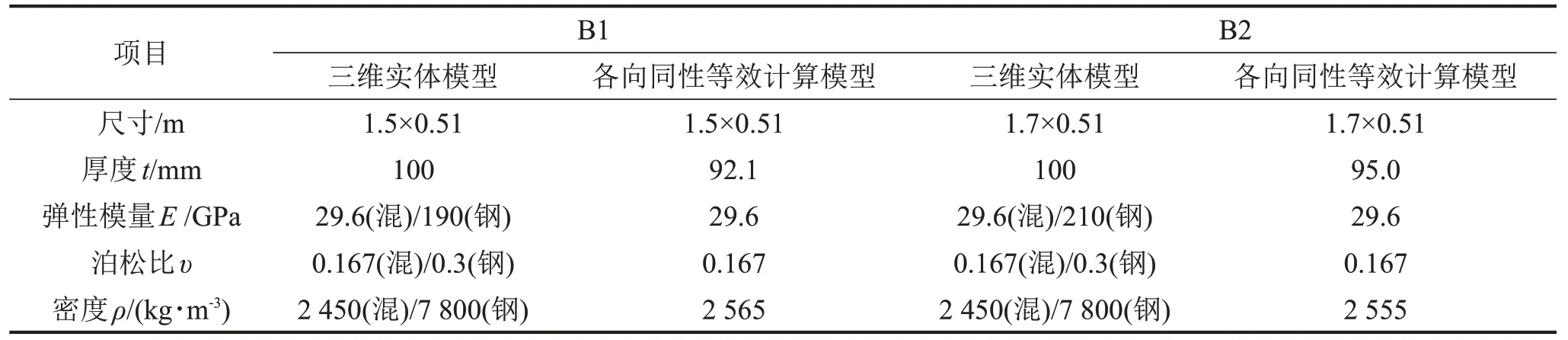
表6 組合樓板的三維實(shí)體模型和各向同性等效模型的參數(shù)

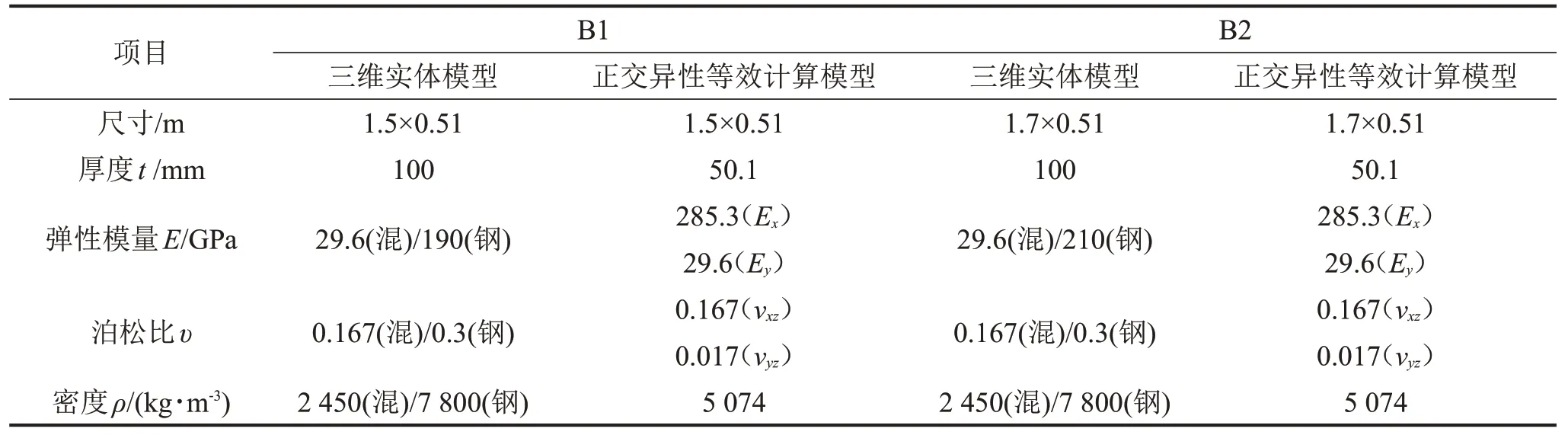
表7 組合樓板的三維實(shí)體模型和正交異性等效模型的參數(shù)

組合樓板的三維實(shí)體模型和等效模型圖如圖10所示。

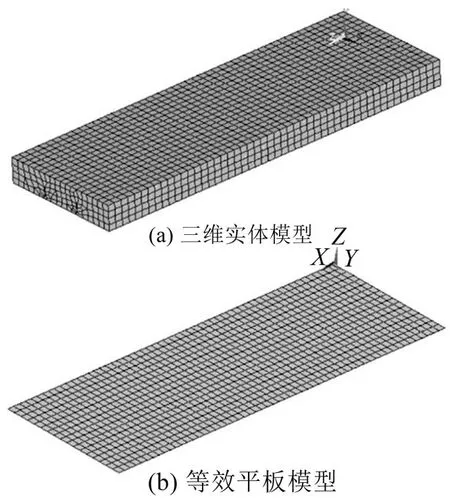
圖10 組合樓板有限元模型

3.2 模態(tài)分析結(jié)果的比較

試驗(yàn)結(jié)果與根據(jù)三維實(shí)體模型、各向同性等效計(jì)算模型、正交異性等效計(jì)算模型求解得到的1 階振型和基頻（取3次測試的均值）的對比如圖11和表8所示。

圖11 試驗(yàn)與模型仿真所得1階振型對比

由圖12 和表8 可以看出：三維實(shí)體模型和二種等效模型的1 階振型基本一致；使用三維實(shí)體模型和兩種等效計(jì)算模型得到的基頻與試驗(yàn)誤差均在6.5%以內(nèi)；正交異性等效模型與三維實(shí)體模型的基頻誤差均在0.6%以內(nèi)，而各向同性等效模型與三維實(shí)體模型基頻的誤差達(dá)到了11%左右，因此使用正交異性等效模型簡化樓板可以得到更加精確的結(jié)果；使用二種簡化模型求解所需時(shí)間僅為三維實(shí)體模型的1.5%左右。

表8 試驗(yàn)與模型的基頻對比

3.3 激振試驗(yàn)結(jié)果的比較

在ANSYS 中利用諧響應(yīng)分析模擬激振荷載對樓板的作用，施加的激振力幅值與頻率范圍與試驗(yàn)相同。分別求得組合樓板的三維實(shí)體模型、各向同性等效模型和正交異性等效模型的跨中峰值加速度并與激振試驗(yàn)測得的結(jié)果對比，取荷載幅值為4 N、12 N、20 N進(jìn)行分析，根據(jù)3種模型所得結(jié)果與試驗(yàn)結(jié)果對比情況如圖12至圖14所示。

從圖12至圖14可以看出：根據(jù)三維實(shí)體模型和正交異性等效模型求得的峰值加速度與試驗(yàn)結(jié)果具有良好的一致性，而根據(jù)各向同性等效模型所得的結(jié)果與試驗(yàn)結(jié)果有一定誤差；采用各向同性等效模型與正交異性等效模型均能大大簡化建模過程，且使諧響應(yīng)分析的求解時(shí)間僅為三維實(shí)體模型的10%左右。

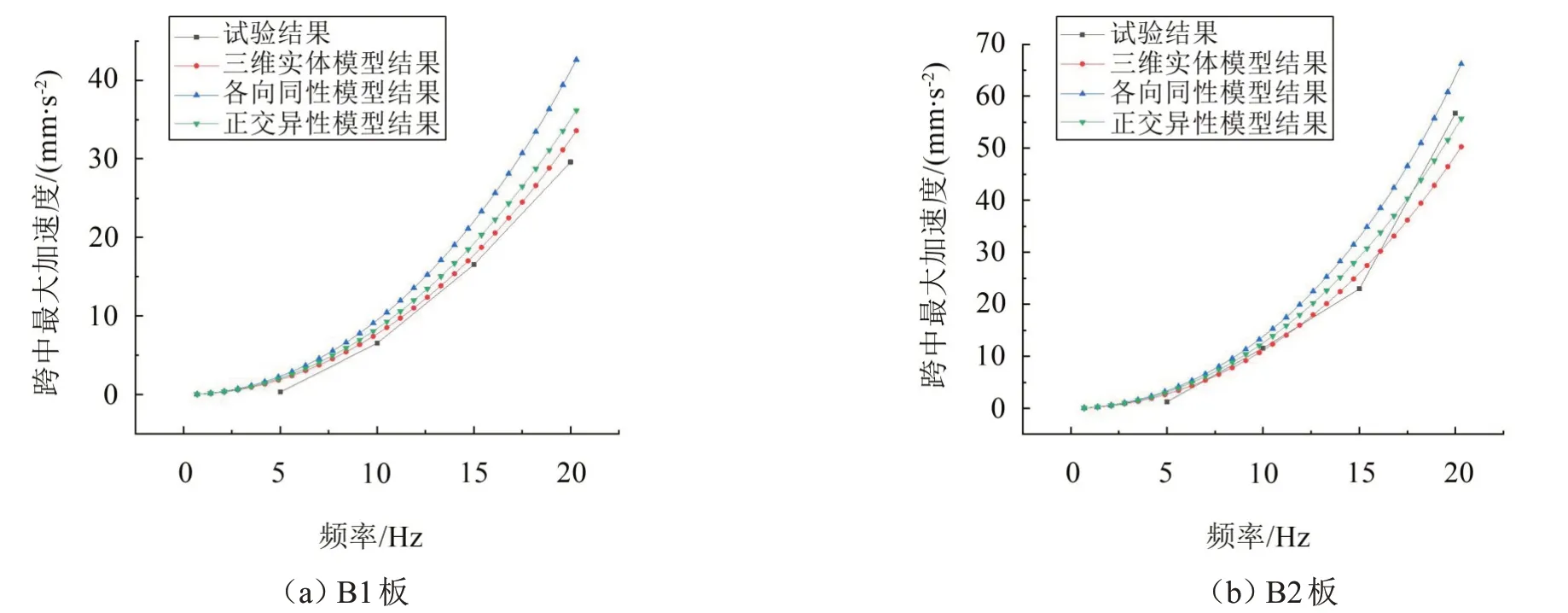
圖12 試驗(yàn)與模型仿真所得加速度對比（激振幅值為4 N）

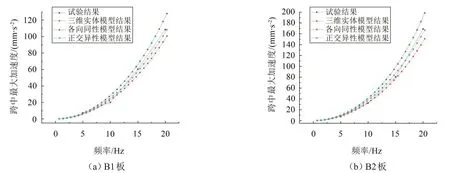
圖13 試驗(yàn)與模型仿真所得加速度對比（激振幅值為12N）

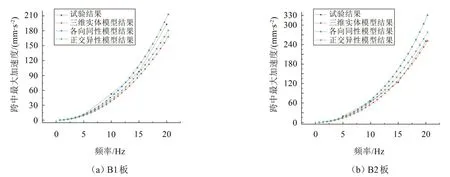
圖14 試驗(yàn)與模型仿真所得加速度對比（激振幅值為20 N）

4 結(jié)語

本文針對閉口型壓型鋼板-混凝土組合樓板的振動(dòng)問題，建立了各向同性等效平板模型和正交異性等效平板模型，通過有限元分析和樓板振動(dòng)試驗(yàn)結(jié)果對比分析，得到如下結(jié)論：

（1）對大跨度、多層的組合樓板體系進(jìn)行環(huán)境振動(dòng)問題的分析時(shí)，將其簡化為各向同性等效模型或正交異性等效模型是可行的，可以大大簡化建模過程、顯著提高計(jì)算效率。

（2）根據(jù)各向同性等效計(jì)算模型、正交異性等效計(jì)算模型得到的結(jié)果與組合樓板模態(tài)試驗(yàn)所得結(jié)果、激振試驗(yàn)所得結(jié)果都有著良好的一致性。根據(jù)正交異性等效模型得到的基頻與三維實(shí)體模型誤差僅為0.6%，而根據(jù)各向同性等效模型得到的基頻與三維實(shí)體模型的誤差接近11%；在進(jìn)行諧響應(yīng)分析時(shí)，根據(jù)正交異性等效計(jì)算模型求得的峰值加速度與試驗(yàn)結(jié)果更為接近。

（3）總體上，兩種等效計(jì)算模型均有一定的應(yīng)用價(jià)值，但正交異性等效計(jì)算模型相較于各向同性等效計(jì)算模型更為精確，在環(huán)境振動(dòng)建模分析中可優(yōu)先采用。