譜方法求解水聲傳播問題的優化與并行*

馬 現，王勇獻，朱小謙，屠厚旺，李 朋，顏愷壯

(國防科技大學氣象海洋學院，湖南 長沙 410073)

1 引言

近年來，水聲技術被廣泛應用于水下通訊[1]、海洋環境測量[2]和海底測繪[3]等各個方面。海洋中聲波的傳播滿足基本的波動方程，但由于海洋環境的時空復雜性，聲場分布易受環境的影響，導致聲波在海水中的傳播異常復雜[4]。波動方程是所有的聲傳播數學模型的理論基礎，至今已發展出了多種傳播模型[5]，目前利用數值模型進行水聲傳播計算已經成為最常用的研究手段之一。

經典的水聲傳播計算模型包括簡正波近似法、拋物方程近似法等。每一種模型均是對原始波動方程在特定條件下的近似，需求解一組微分方程。在傳統水聲傳播數值模擬中，有限差分方法是最常用的離散方法之一。例如，Porter等人[6]在簡正波近似法中使用有限差分離散的方法，開發了Kraken程序；Collins等人[7]在拋物方程近似法中使用有限差分離散的方法，擴展了針對二維寬水平傳播角情況的RAM(Range dependent Acoustic Model)程序；Lee等人[8]利用有限差分法開發了三維拋物模型的FOR3D程序;石鈴林等人[9]進一步對拋物方程模型和FOR3D程序的聲傳播規律進行了研究。盡管有限差分離散在傳統水聲傳播計算中發揮了重要作用，但它仍然存在很多不足，如處理復雜的邊值問題時不夠靈活，構造高精度的差分格式困難等。

在計算流體力學、地震波傳播等其它方面，譜方法由于具有精度高、收斂速度快等優點[10-12]，利用其進行數值離散也得到了學者們的青睞。20世紀80年代，韋達[13-18]對譜方法的理論進行了系統研究，發現譜方法無窮階的收斂特性；譜方法在物理方面也得到了廣泛的應用，如大氣環流[19]、數值渦流[20]等；近年來，一些學者嘗試將譜方法引入到水聲傳播的數值計算中，取得了較好的效果，Tu等人[21]最近提出了一種可以解決不連續分層問題的簡正波-譜方法數值模擬新手段，用于求解經典的簡正波模型，可以處理聲速、密度和衰減剖面不連續的問題，并開發了相應的NM-CT(Normal Mode model program based on the Chebyshev-Tau spectral method)程序，計算結果具有較高的精度。

大海域、高頻聲源等復雜場景中的高精度聲場模擬仍然面臨著計算量較大、模擬速度慢和實時性不足等問題，難以滿足水下實際應用場景中聲場快速分析的需求。隨著高性能計算技術的迅速發展，利用高性能平臺研究水聲傳播優化與并行算法，為解決這個問題提供了新的途徑。對于簡正波模型，吉虹宇[22]基于并行應用框架OpenFOAM實現了水聲傳播并行數值模擬；對于拋物方程模型，范培勤等人[23]實現了弱三維情況下FOR3D模型的并行計算，徐閩等人[24]在高性能平臺天河二號上實現了FOR3D模型的并行計算，王魯軍等人[25]使用共享存儲并行編程(OpenMP)方法在多核計算機上實現了RAM程序的并行，均取得了較好的加速效果；對于射線模型，Xiao等人[26]在高性能計算平臺上，利用OpenMP對三維楔形海底的水聲傳播模型進行并行加速與優化；Zhu等人[27]綜合利用串行優化和并行加速的方法，在天河二號高性能計算平臺上對三維水聲傳播模型進行了優化和并行加速，同樣也取得了較好的效果。

本文擬針對譜方法求解大規模水聲傳播問題過程中，計算速度慢、實時性差等問題，面向主流眾核平臺開展程序的優化與并行，加速數值模擬。

各個章節主要內容如下：第1節主要介紹譜方法求解水聲傳播問題的現狀與存在的問題；第2節主要介紹譜方法求解水聲傳播問題的原理及其計算流程；第3節介紹譜方法求解水聲傳播問題的優化與并行方法；第4節給出了在天河二號高性能計算平臺上的數值測試結果，并對優化效果進行詳細分析和評估；第5節對全文的工作進行總結，展望后續研究。

2 譜方法求解水聲傳播問題的原理及計算流程

考慮一個關于深度z和水平距離r的二維水聲傳播問題，設聲源角頻率為ω、深度為zs，聲壓為p(r,z)，密度為ρ，聲速為c，聲音傳播介質(海水及海底沉積底)是水平分層的，則在聲源點以外的空間，聲壓滿足Helmholtz方程，如式(1)所示：

(1)

采用分離變量法求解該方程，則有p(r,z)=ψ(z)R(r)，其中R(r)為漢克爾函數，ψ(z)滿足如式(2)所示的常微分方程：

(2)

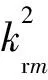
(3)

其中i為虛數單位。利用譜方法求解式(2)的基本思路是把解函數在一簇光滑的基函數上作近似展開(即譜展開)，將原始物理空間中的問題轉化為譜空間中求解展開系數的問題。下面以Tu等人[21]提出的Chebyshev-Tau譜方法計算簡正波模型和其開發的NM-CT程序(用Fortran語言開發的開源代碼，可從https://oalib-acoustics.org/Modes/index.html下載)為例，簡要介紹譜方法求解水聲傳播模型的流程。

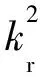
(4)

其中k表示波數。利用算子￡代替式(4)左側作用于ψ(x)的算子，則式(4)簡化為式(5)：

(5)

其中,對定義在[-1，1]上的任意光滑函數ψ(x)使用Chebyshev變換，即利用Chebyshev多項式Tmp(x)展開(mp表示譜方法的截斷階數)并對無窮項作有限的N階截斷近似處理，如式(6)所示：

(6)

(7)

利用Chebyshev變換將式(5)由原始的物理空間變換到譜空間，最終形成一個線性代數特征值系統，寫為矩陣形式如式(8)所示：

(8)

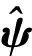
輸入:初始聲速、密度、聲源位置和頻率等物理量。

步驟1利用Chebyshev多項式展開ψ(x)，離散式(2);

步驟2求解式(8)特征值和特征函數;

步驟3利用Chebyshev變換求得矩陣L的特征解;

步驟4計算漢克爾函數R(r);

步驟5計算聲壓p;

步驟6計算TL。

算法包含如下3個主要的計算函數，第1個計算函數即算法第1～2行，命名為EIGsolve。EIGsolve函數主要計算式(8)矩陣L的特征值。第2個計算函數即算法第3行，命名為Genemodes。Genemodes函數主要對矩陣L的特征值和特征函數進行Chebyshev變換，得到每個簡正波模態函數ψm,m=1,2,…。第3個計算函數即算法第4～6行，也是算法計算量最大的部分，命名為Syn。Syn函數主要計算聲壓p和傳播損失TL。

譜方法與有限差分方法相比，是一種高精度的計算方法，兩者的水聲計算精度的對比在文獻[21]中有詳細分析。以文獻[21]分析的存在解析解的算例1為例，與有限差分方法相比，譜方法在垂直方向離散點更少的情況下取得更高的精度，適合于對聲場計算精度需求較高時的場景。下面以NM-CT程序為例，分析譜方法求解水聲傳播問題的優化方法和并行方案，詳細描述每種優化方法的原理并對測試結果進行分析。

3 程序的優化方法與并行方案

為了使程序性能優化與并行工作更有針對性，本文利用Vtune工具測試和分析原始NM-CT串行程序，各個函數的耗時比例為：EIGsolve約2.91%，Genemodes約0.23%，Syn約54.95%，顯然，程序的主要時間開銷集中在Syn函數。因此，后續著重針對Syn函數進行優化與并行。首先對原始串行程序進行不同層次的優化，主要包括：編譯器調整和優化、調用高性能數學庫MKL、優化訪存和精簡計算等；其次針對高性能眾核計算平臺，對調優后的代碼進行多線程并行加速，以充分利用多核心的計算資源。

3.1 串行優化

串行代碼性能優化與并行優化同等重要，且極有可能獲得大幅度的加速效果，因此首先對代碼進行串行優化是非常必要的。

3.1.1 編譯器優化

由于編譯器首先會對代碼整體進行優化，首先測試GNU 的gfortran和Intel的ifort 2種編譯器對代碼性能的影響。在保證正確性的基礎上選用優化級別更高的編譯器-O3、添加選項-ipo過程間優化和-funroll-all-loops循環展開選項對代碼進行優化。

3.1.2 利用高性能數學庫MKL

較大規模的矩陣乘法計算耗時比較突出，利用Intel公司開發的計算速度更快的MKL庫函數GEMM來替換原始的矩陣乘計算，以提升運算速度。

3.1.3 訪存優化

在代碼的優化過程中，訪存也是影響代碼運行速度的一個重要因素，保證訪存的連續性提升Cache命中率并盡可能減少內存的使用，對代碼的性能有較為明顯的提升。

在提升Cache命中率方面，在讀取數據的過程中，按照存放順序讀取，可以保證較高的緩存命中率。以NM-CT代碼計算矩陣L為例，EIGsolve函數的部分代碼如下所示：

簡化前的函數:

1dok=1,size(v)

2doi=1,size(v)

3doj=1,size(v)

4if((i-1+j-1)==(k-1))

5Co(k，i)=Co(k，i)+v(j)*0.5;

6if(abs(i-j)==(k-1))

7Co(k，i)=Co(k，i)+v(j)*0.5;

8enddo

9enddo

10enddo

簡化后的函數:

1n=size(v);

2doi=1,n

3dok=1,n

4j=k-i+1;

5if(1 ≤j.and.j≤n)then

6Co(k,i)=Co(k,i)+v(j);

7endif

8j=i-k+1

9if(j≤n.and.j≥1)then

10Co(k,i)=Co(k,i)+v(j);

11endif

12Co(k,i)=Co(k,i)* 0.5;

13enddo

14enddo

簡化前的函數為原始循環方式，代碼第1、2行改進后，按照簡化后的函數中第2、3行所示的方式，大大提高了Cache命中率，對程序性能的提升有較為明顯的作用。

在減少內存使用方面，訪存優化更直接有效的方式是減少內存的使用。通過分析可以刪減部分不必要的數組，減少內存空間的使用。以NM-CT代碼計算psi數組為例，計算psi數組的具體過程如下所示：

改進前的計算:

1doi=1,nmodes

2psizs(i,i)=psi(…,i)*(…)+psi(…,i)*(…);

3enddo

4psi=matmul(psi,psizs);

改進后的計算:

1doi=1,nmodes

2psi(:,i)=psi(:,i)*[psi(…,i)*(…)+

3psi(…,i)*(…)]

4enddo

改進前的計算中，對psi數組的更新僅僅是將其每一列元素乘一個相同的數，即psizs對應的元素值，因此直接將數組psi的每一列元素乘原數組,如改進后的計算。通過分析發現，改進后的計算可以少開辟一個維度nmodes×nmodes的數組，減少了內存的使用，加快了其運行速度。

3.1.4 精簡計算

程序中包含有大量的計算過程，若能夠有效去除冗余計算，整個程序會有較大幅度的性能提升。對NM-CT的簡化計算主要是減少分支判斷語句。以EIGsolve函數的計算為例，利用譜方法計算矩陣L時，部分代碼如簡化前的EIGsolve函數所示。三重嵌套循環最內層第4、5行賦值語句所需j索引值可以用i和k表示，從而極大地減少生成指令中的循環分支語句數目，有利于串行代碼的指令級調度與優化。

3.2 并行優化

當程序中含有大量的循環和數據計算時，采用并行計算是最有效的提速方法。以NM-CT中的Syn函數計算為例，其包含有大量的循環和數據計算，因此這個函數中的代碼是可以并行計算的熱點代碼段。

(1)OpenMP多線程并行方案設計。

在循環計算中，若各個計算之間相互獨立，則采用任務并行的策略，直接利用OpenMP多線程并行，還可以直接利用collapse對兩重循環進行展開,從而增大了并行度，并且可以保證線程間的負載均衡；在調度的過程中，嘗試靜態和動態等多種不同的調度方式，尋找最優的調度方式。以Syn函數中的計算為例，嵌套循環的并行過程如下所示：

1 !$omp parallel default(none)&

2 !$omp shared(…)private(…)

3 !$omp do collapse(2)schedule(static,…)

4doi=1，nr

5dok=1，nmodes

6bessel0=r(i)*kr(k);

7 callZBESH(…);

8bessel(k，i)=cmplx(CYR，CYI)

9enddo

10enddo

11 !$omp end do

12 !$omp end parallel

上述第3行代碼，循環內的計算沒有依賴關系，直接利用OpenMP多線程并行，用collapse對兩重循環進行展開，并且嘗試多種不同的調度方式，尋找效率最高的計算方式。

(2)利用多線程高性能計算庫MKL。

與OpenMP多線程相適應，通過調用多線程版本的高性能計算庫MKL，可實現矩陣相乘GEMM函數的多線程加速，進一步提升計算速度。

4 實驗與結果分析

4.1 高性能平臺簡介

為了檢驗本文所用的優化方法的效果，在高性能平臺天河二號上進行了測試。天河二號高性能計算平臺的CPU 為Intel(R)Xeon(R)CPU E5-2692，每個結點包含2個CPU，每個CPU包含12個核。在測試過程中，采用gcc/6.3.0版本和Intel-compilers/mkl-15 2種編譯器進行測試。在實際測試過程中，對于每一次優化都進行5次測試，將時間最短的測試時間作為最優時間。

4.2 算例

譜方法求解水聲傳播模型能夠對多種復雜的算例和模型進行數值模擬。選取具有代表性的Munk波導算例進行測試(本文所有圖表的彩色版本可從https://gitee.com/maxian-nudt/nm-ct_-parallel/issues下載)。

Munk剖面是一個理想化的聲速剖面，它可以刻畫深海聲場傳播的規律與特征，聲源位于1 000 m處，頻率為50 Hz，水層密度為1.0 g/cm3，沉積層密度為1.5 g/cm3，水層衰減系數為0，沉積層衰減系數為0.01,水層深度為2 500 m，沉積層深度為5 000 m。Munk波導的聲速值為c(z)=1500.0[1.0+其中,圖1a展示了利用譜方法畫出的傳播損失場。圖1b展示了海深1 000 m處利用不同方法計算的TL值，此算例不存在解析解，因此用傳統有限差分方法的程序代碼Kraken的計算結果作為參考解。從圖1中可以看出，截斷階數N值越大，計算結果越精確。考慮實際復雜海洋環境對計算精度的要求以及算法整體計算量的大小，選擇N=1 000進行計算和后續的測試分析。

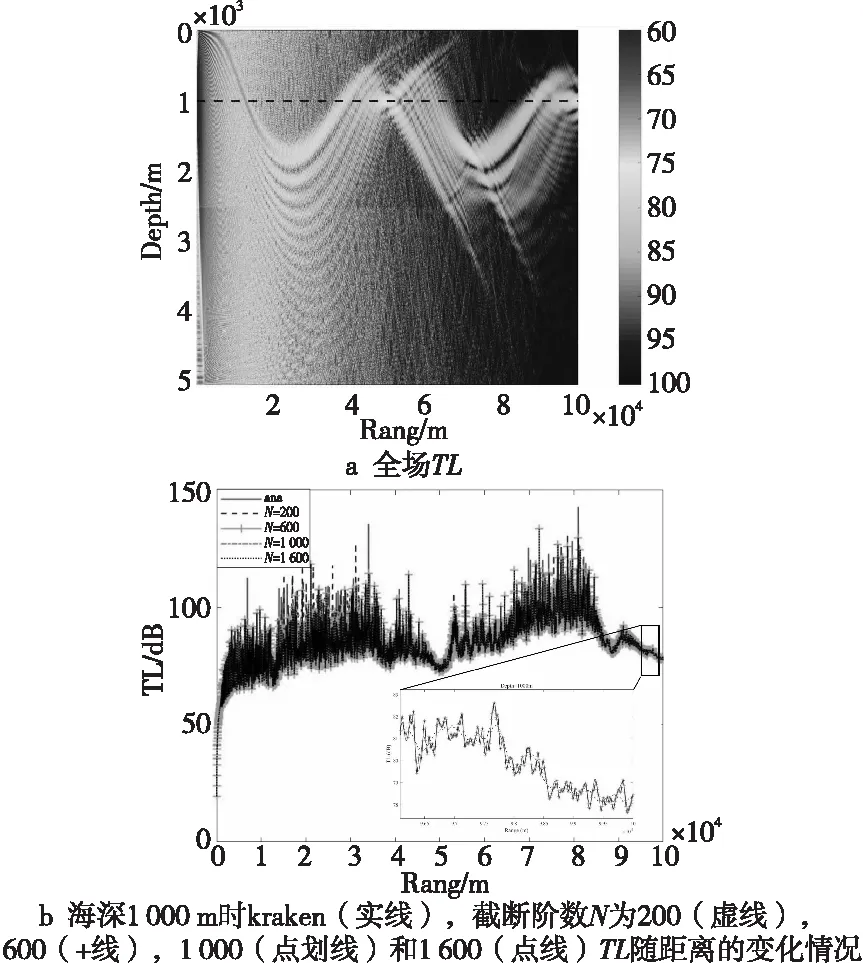
Figure 1 TL schematic diagram of Munk

4.3 串行優化結果與分析

4.3.1 編譯器和編譯選項優化

表1為原始串行程序在天河二號高性能平臺上不同編譯器和編譯選項的測試結果：選用Intel編譯器并增加合適的編譯選項可使性能進一步提升。以gfortran編譯器下的-O2選項為基準，通過更換編譯器及編譯選項優化，最終獲得了1.67倍的加速效果。

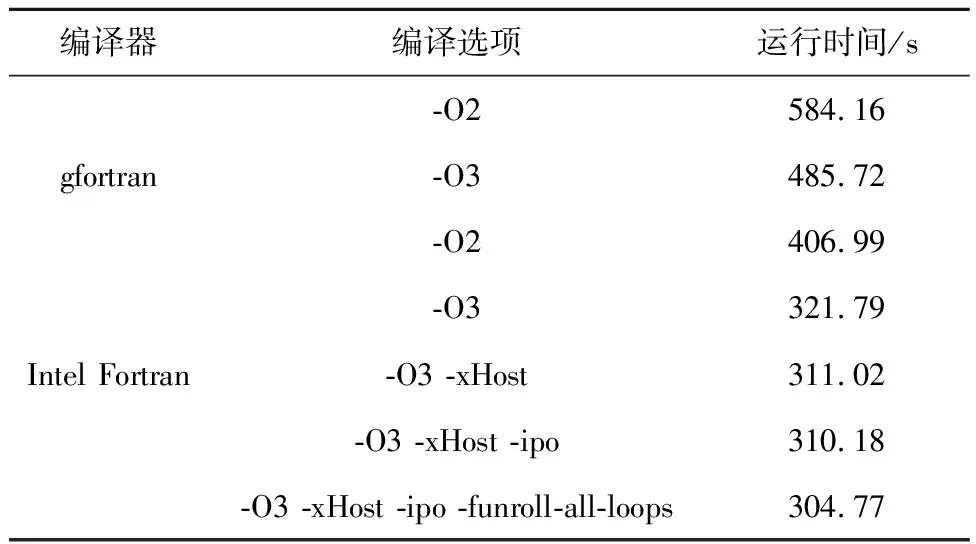
Table 1 Effects of different compilers and compilation options on running time of serial programs

4.3.2 利用高性能數學庫MKL

測試計算聲壓大規模矩陣乘法代碼段在使用MKL庫前后的運行時間，時間由201.2 s減少至56.83 s，使用MKL庫后運行時間縮短144.37 s，提速3.54倍。

4.3.3 訪存優化

在提升Cache命中率方面，對程序進行訪存優化，首先對計算矩陣L的兩重嵌套循環交換循環嵌套的順序，使訪存滿足空間的連續性，該代碼段優化后運行時間由3.03 s減少至2.79 s。

在減少內存使用方面，通過分析具體計算過程，省略psizs數組，將運算簡化，該代碼段運行時間由0.58 s減少至0.003 s。

根據訪存連續性的原理，對整個程序的嵌套循環和數組進行檢查，最大限度地保證訪存的連續性，優化后進行測試，運行時間由304.77 s減少至288.13 s，運行時間減少了16 s，加速了1.05倍。訪存優化不僅提升了程序性能，且精簡了代碼，有利于后續對代碼的維護。

4.3.4 精簡計算

對計算矩陣L的部分代碼減少分支判斷語句后，計算量大大下降，測試優化前后每次調用此函數所需要的時間由3.03 s減少至0.02 s。由于調用矩陣L次數較多，測試簡化運算后對整個程序性能的影響。測試結果表明，程序運行時間由304.77 s減少至242.19 s，對代碼進行簡化后，程序運行時間減少了62 s，加速了1.26倍。

圖2主要展示了串行優化前后3個主要函數的運行時間變化。串行優化效果最為明顯的是Syn函數，Syn函數利用了MKL替換原始矩陣乘計算、訪存優化和精簡計算3種方法。優化后Syn函數運行時間由320.91 s減少至80.43 s，加速比達到3.26，串行加速方法的有效性得到了證實。

Figure 2 Time changes of the three main functions and the total time before and after serial optimization

4.4 并行優化

并行加速效果遵循Amdahl加速比定律[27]，據此可提前預判最優的并行效果。在眾核平臺上，若可以使用的最大線程數為nt，程序代碼中可并行部分的執行時間所占百分比為q，則理想加速比S=1/(1-q+q/nt)。

本文對3.2節的并行方法進行了測試。首先對熱點Syn函數內部的3個主要步驟(計算R(r)、計算聲壓、計算TL)進行多線程并行，測試不同線程數目下的運行時間，結果如表2所示。

Table 2 Program running time under different thread numbers

通過多線程并行加速后程序的總運行時間由串行最優版本的93.94 s減少為24.38 s，熱點函數Syn的運行時間由原來的80.43 s減少至9.84 s。當線程數為24時，整個程序的理想加速比S=5.68，實際并行后的絕對加速比為3.85，未達到理想值。究其原因，可能是由于串行程序中部分可并行的代碼之間夾雜部分不可并行的計算，需要多次進行開關線程的操作，導致程序運行時間增加，對程序的優化效果產生不良影響。

圖3顯示了Syn函數中3個子計算步驟的加速比情況。由于各網格點之間的計算沒有依賴，因此多線程并行計算具有良好的加速效果。隨著線程數的增加，加速比基本呈線性增長。當使用24個線程時，計算R(r)的代碼段加速比可達17.59。圖3中虛線表示對應線程數目下的最優加速比。

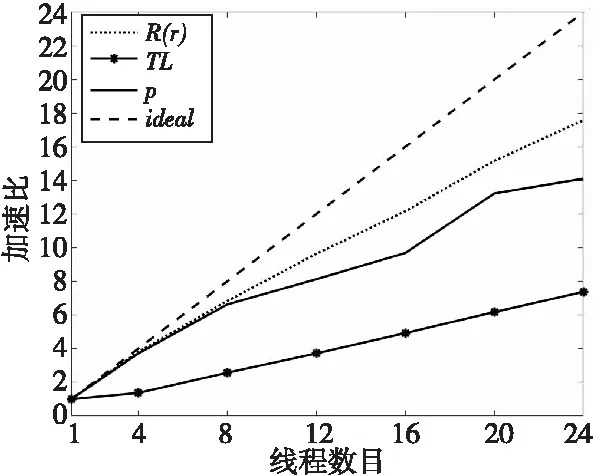
Figure 3 Speedup of R(r),TL, and p under different thread numbers, and the optimal speedup under the corresponding number of threads

此外，為了進一步測試多線程并行的任務調度對性能的影響,對Syn函數中的計算TL步驟進行了測試，圖4展示了使用動態調度以及不同粒度參數下的靜態調度時代碼的執行時間。結果表明靜態調度隨著塊中的迭代次數chunksize值的增加，耗時逐漸減少，當chunksize值達到1 024時，該代碼段的耗時達到最低。

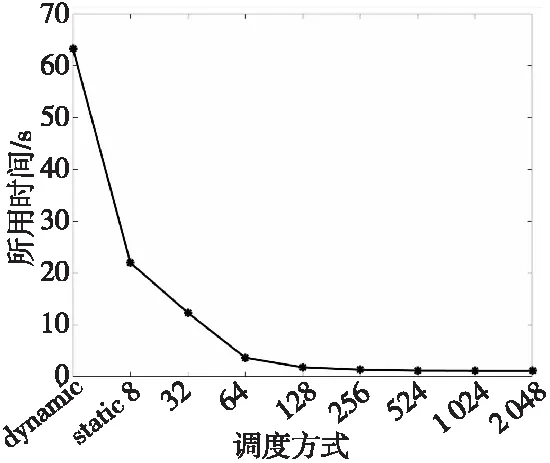
Figure 4 Different scheduling methods to calculate the time change of TL under 24 threads

4.5 優化前后結果對比

對程序進行串行和并行優化后，需要對程序改進前后的計算結果進行對比分析，比較計算結果精確度的變化，取聲源深度1 000 m的計算結果進行比較，如圖5所示。

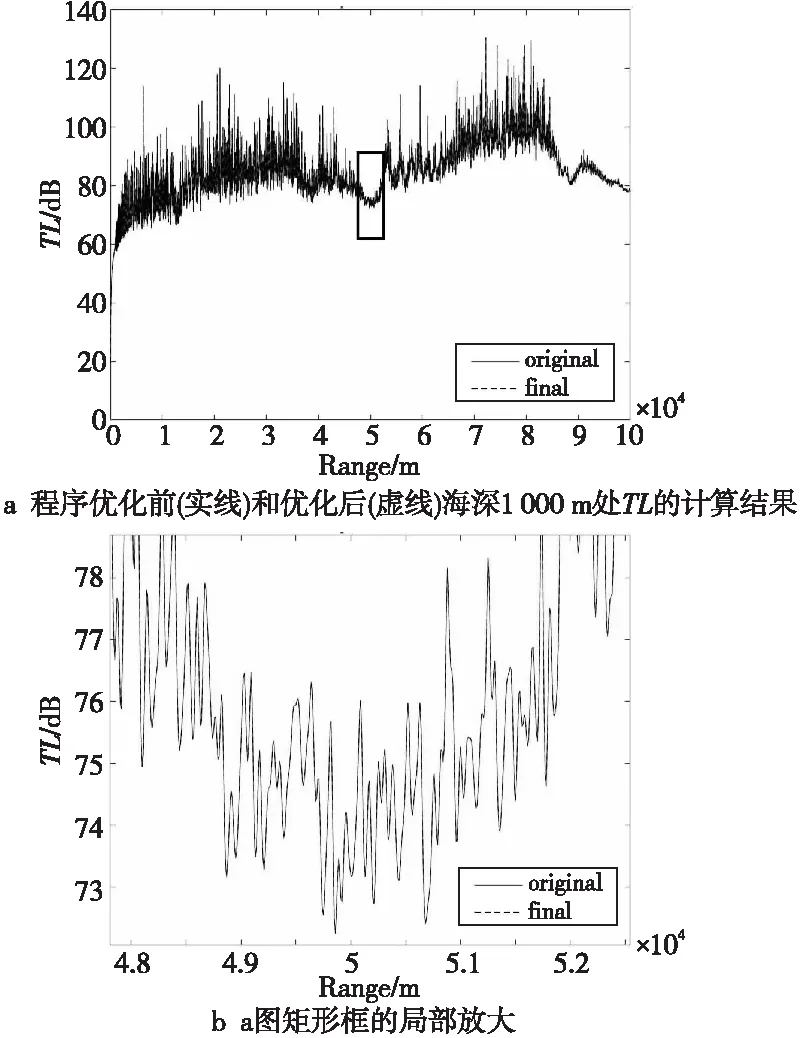
Figure 5 Comparison of calculation results before and after optimization

根據圖5優化前后的計算結果，可以看出2條曲線基本重合，程序改進前后計算結果非常接近，表明此次優化沒有改變程序計算結果的精度。

4.6 實驗結果分析

綜上所述，通過綜合使用串行優化和多線程并行加速技術，分層海洋聲傳播Chebyshev-Tau譜方法程序NM-CT的性能得到了提升，計算效率大幅提升。以gfortran編譯器作為基準版本，程序原始版本的運行時間為584 s，優化與并行的各階段的加速效果如表3所示。

Table 3 Changes in program performance under different optimization techniques

通過結果對比發現，首先選擇合適的編譯器對程序性能的提升有較大的作用，對于NM-CT程序，在天河二號的平臺上 Intel 的 ifort 編譯器對提升此程序的性能作用更加顯著。此外，加入合適的附加編譯選項、使用高性能MKL 函數庫、優化訪存和合理簡化計算等串行優化方法，在單結點單線程下，充分利用了資源，取得了較好的加速效率。利用并行加速方法，并在此基礎上研究不同調度策略以及chunksize大小對程序的影響，發揮眾核潛能，進一步提升了程序的運行速度。針對天河二號單結點，本文提出的關于 NM-CT 程序的一系列優化和并行加速方法非常有效，程序運行時間從原始的584 s減少到最佳優化版本的24 s，加速了23.98倍，優化效果明顯，極大地提升了程序的性能，對解決計算大范圍海域聲傳播實時性問題做出了重要的貢獻。

5 結束語

為解決譜方法數值求解水聲傳播問題計算量大、實時性差等問題，本文充分利用高性能計算平臺對譜方法求解水聲程序進行性能優化與并行加速，首先從選擇合適的編譯器和優化選項、調用高性能數學庫MKL函數、訪存優化和精簡計算4個方面對串行程序內部進行優化;接下來在天河二號眾核平臺上對程序進行更細粒度、更輕量級的多線程并行，在此基礎上研究不同調度策略和chunksize大小對程序性能的影響。以NM-CT程序為例測試優化與并行手段的加速效果，結果表明，本文所使用的優化與并行方法，對于加速譜方法數值求解水聲傳播問題有非常明顯的加速效果，計算深海波導程序運行時間由原始串行版本的584 s減少到24 s，加速了23.98倍，顯著提高了程序的運行效率。進一步分析程序，若截斷階數更高，導致EIGsolve函數耗時較長，因此在下一步的工作中，需要進一步對程序在截斷階數更高的情況下進行優化。盡管對于實際的大范圍海域聲場計算仍沒有達到實時處理的要求，但本文的工作為達成這一目標邁進了一大步。