融合雙層注意力機制的屬性網絡節點嵌入*

楊凡億，馬慧芳,2，閆彩瑞，宿 云

(1.西北師范大學計算機科學與工程學院，甘肅 蘭州 730070;2.桂林電子科技大學廣西可信軟件重點實驗室,廣西 桂林 541004)

1 引言

網絡在現實世界中無處不在，其中屬性網絡近年來引起了學者的廣泛關注。與僅提供拓撲結構的普通網絡相比，屬性網絡除了具有復雜的結構關聯，節點也擁有與結構互補的豐富屬性信息，有效地利用這些屬性信息可以使網絡分析受益。現有的研究表明節點的屬性可以反映并影響其社區結構[1,2]。因此，面向屬性網絡的研究方興未艾。典型的屬性網絡包括學術引文網絡和社交網絡等。在學術引文網絡中，不同文章之間引用關系形成一個網絡，其中每個節點代表文章，并且每個節點附著著和文章主題相關的大量文本信息；在社交網絡中，除了用戶之間密切的交流外，用戶的個人資料也可以作為屬性信息。

網絡嵌入作為網絡分析的基本工具，是近年來的研究熱點。該研究是在保留近似的同時學習網絡中節點的低維表示，然后用于節點分類[3]、節點聚類[4]和鏈接預測[5]等下游任務。例如，基于隨機游走的DeepWalk[6]采用截斷隨機游走方式，從網絡中每個節點出發，游走遍歷網絡中的其他節點得到若干節點序列，根據窗口獲取采樣節點的上下文節點，然后運用skip-gram模型最大化隨機游走序列的似然概率。LINE(Large-scale Information Network Embedding)算法[7]在網絡上定義了一階相似度和二階相似度，并最小化表示相似度與實際相似度的KL散度得到節點的表示。node2vec[8]為了挖掘網絡結構的特性，引入2個超參數控制隨機游走的策略，將得到的特定節點序列輸入到skip-gram模型中以學習節點表示。上述經典方法只考慮了網絡的拓撲結構信息，沒有將節點的屬性信息考慮進去。研究人員面向屬性網絡已提出各種各樣的嵌入模型。針對屬性網絡得到的節點低維表示，可以使具有拓撲和屬性相似的節點在嵌入空間彼此接近。經典的工作包括：Yang等人[9]在矩陣分解的框架下，提出TADW(Text-Associated DeepWalk)算法，將節點的文本特征引入到網絡表示學習中。Gao等人[10]提出深度屬性網絡嵌入DANE(Deep Attributed Network Embedding)算法，通過捕捉結構與屬性的高度非線性關聯，在拓撲結構和節點屬性上保持近似性特征，同時該算法可以從拓撲中學習結構和節點屬性的一致和互補表示形式。

作為人類不可或缺的復雜認知功能之一，注意力機制[11]是指人在關注一些信息的同時可以忽略另一些信息的選擇能力，已在眾多研究領域[12-14]得到了廣泛應用。本質上，注意力機制通過對模型中不同部分賦予不同權重，獲取模型中更加重要的和關鍵的信息，從而優化模型并做出更為準確的判斷。為了充分利用節點屬性信息以及隱含在節點-屬性中的語義信息，本文結合注意力機制，提出一種融合雙層注意力機制的屬性網絡節點嵌入算法NETA(Node Embedding combining Two-level Attention mechanism on attributed network)。該算法的主要步驟如下：首先，構造結構-屬性交互二部圖，捕獲直接鄰居和間接鄰居；其次，設計節點級注意力，考慮節點鄰居的相對重要性，分別聚合直接鄰居表示和間接鄰居表示；最后，基于語義級注意力融合2種嵌入表示得到最終嵌入。在人工數據集和真實數據集上設計了不同的實驗來驗證本文算法的有效性。

2 問題定義

令G=(V,E,F)表示屬性網絡，其中V={v1,v2,…,vn}表示節點集合，E?V×V表示邊集，F={f1,f2,…,fm}表示屬性集合，n為屬性網絡中節點總數，m為屬性網絡中屬性總數。矩陣An×n為拓撲結構鄰接關系矩陣，若節點vi與節點vj之間存在邊，則Aij=1,否則Aij=0。矩陣Qn×m表示節點-屬性關系矩陣，若節點vi具有屬性fj，則Qij=1,否則Qij=0，Qi是節點vi的屬性向量。

給定一個屬性網絡G=(V,E,F)，屬性網絡嵌入的目標是學習一個映射函數，將圖G中的每個節點映射到一個低維的向量空間中，使得具有拓撲和屬性相似的節點在低維空間彼此接近。

為了描述清晰起見，將本文主要用到的符號及其含義總結如表1所示。

3 融合雙層注意力機制的屬性網絡節點嵌入NETA

3.1 結構-屬性二部圖

結構-屬性交互二部圖通過“節點-屬性-節點”的跳轉方式將2個節點聯系起來，能夠清晰地捕獲節點與屬性的關系。值得注意的是，在“節點-屬性-節點”的跳轉方式上，起始節點可能最終會跳轉到其非拓撲鄰居節點上。為了和拓撲結構中的直接鄰居進行區分，本文將其稱為基于屬性關系的間接鄰居。具體定義如下所示：

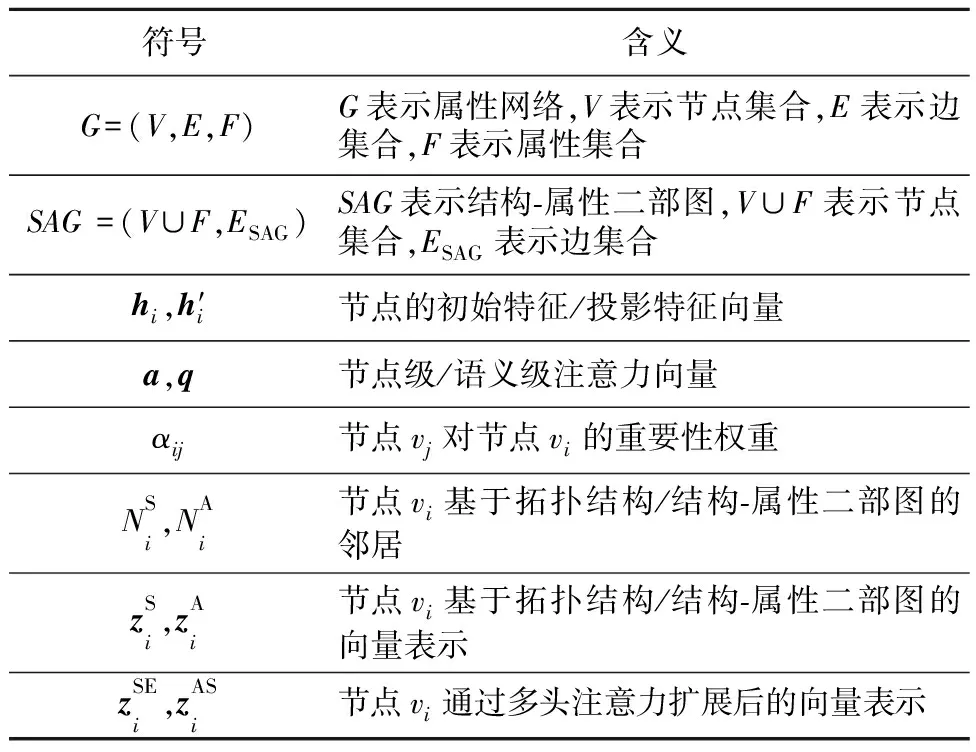
Table 1 Notations and meanings

定義1(結構-屬性二部圖) 結構-屬性二部圖用SAG=(V∪F,ESAG)表示，其中ESAG?V×F。則節點-屬性關系矩陣Qn×m即對應于該二部圖的鄰接矩陣Qn×m。對于?vi∈V,?fj∈F,若節點vi與屬性fj之間存在連邊(即節點vi邊包含屬性fj),則Qij=1，否則Qij=0。

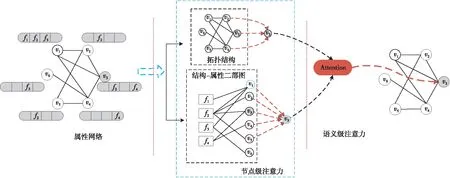
Figure 1 Overall framework of node embedding combining two-level attention mechanism on attributed network

3.2 節點級注意力機制

屬性網絡中每個節點的鄰居扮演著不同的角色，并且在學習節點嵌入中表現出不同的重要性。本節利用注意力機制學習網絡中每個節點鄰居的重要性，并整合這些有意義的鄰居表示以形成節點的嵌入。本文中，節點vi的鄰居包括基于拓撲結構的直接鄰居和基于屬性關系的間接鄰居。基于屬性關系的間接鄰居和基于拓撲結構的直接鄰居相類似，為了節約篇幅，下文中均以基于拓撲結構的直接鄰居為例進行說明。

為了能夠獲得可靠的節點嵌入，本文首先對節點vi的初始特征進行變換，如式(1)所示：

h′i=W1hi

(1)

其中，hi和h′i分別表示節點vi的初始特征向量和變換后的向量表示，W1是所有節點共享的可學習的變換權重矩陣，是模型需要學習的一個參數。將節點的初始特征通過W1進行變換可以得到比初始特征相對好的節點表示，同時可以將節點的向量維度轉換為所需要的維度。

然后，使用注意力機制來學習節點vi鄰居的重要性，并通過聚合這些有著不同權重的鄰居節點以得到節點vi新的特征表示。給定節點vi，通過注意力機制[11]學習節點vj對節點vi的重要性權重αij，其計算方法如式(2)所示：

αij=softmaxj(attnode(h′i,h′j))=

(2)

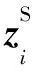
(3)

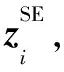
(4)

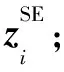
3.3 語義級注意力機制

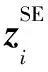
(5)

其中，attsem是一個深度神經網絡，表示語義級注意力。

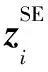
(6)

其中，W2是權重矩陣，b是偏置向量，q語義級注意力向量。同樣地，可以得到結構-屬性二部圖的重要程度wAE。進一步通過softmax函數進行歸一化，可得到拓撲結構的重要性權重，如式(7)所示：

(7)

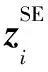
(8)

為了提高所提算法的性能，本文增加一個全連接層用于分類，并利用部分有標簽的節點算法對進行優化，設計交叉熵作為損失函數，如式(9)所示：

(9)

其中，VL是擁有標簽的節點集合，Yi為節點vi的標簽，zi為節點vi的最終向量表示，C是分類器的參數。最后通過反向傳播對模型進行優化，學習節點的向量表示。

3.4 雙層注意力屬性網絡節點嵌入算法步驟

雙層注意力屬性網絡節點嵌入方法步驟如算法1所示。

算法1雙層注意力屬性網絡節點嵌入算法NETA

輸入:屬性網絡G=(V,E,F)，節點初始特征{hi,?vi∈V}，多頭注意力數K。

輸出:最終節點表示Z。

步驟1構造結構-屬性交互二部圖SAG

步驟2特征轉換:?vi∈V,h′i←W1·hi;

步驟3 fork=1..Kdo:

步驟4forvi∈Vdo:

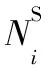
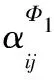
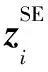
步驟8end

步驟9 end

步驟10根據式(7)計算直接鄰居和間接鄰居的重要性權重βSE和βAE；

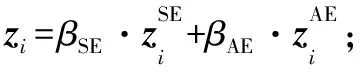
步驟12計算交叉熵損失:L=-∑vi∈VLYiln(C·zi);

步驟13反向傳播和更新參數；

步驟14返回：最終嵌入Z。

4 實驗及結果分析

本節通過在數據集上進行廣泛實驗，來回答以下研究問題，以驗證本文算法的有效性。

問題1NETA在節點分類和節點聚類中性能如何？

問題2NETA對參數的敏感程度如何？

問題3NETA的兩級注意力機制對算法的性能貢獻如何？

本節首先介紹實驗所需的數據集，其次介紹對比算法和實驗設置，最后對實驗結果進行分析并結合案例分析闡釋本文算法的有效性。所有代碼都是使用Python3.7實現。

4.1 實驗數據集

實驗數據集包括真實數據集和人工數據集。表2和表3分別給出了真實數據集的統計信息和人工數據集中的參數及其含義。

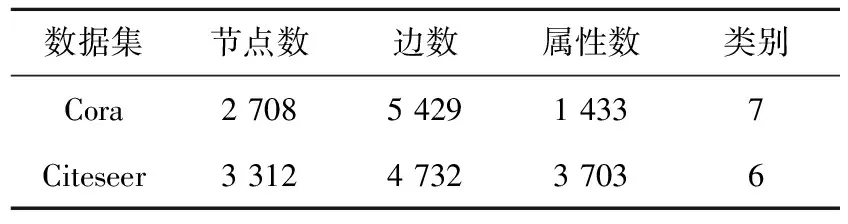
Table 2 Statistics of real-world datasets

Table 3 LFR parameters and meanings

Cora(https://linqs.soe.ucsc.edu/data)是一個科學論文的引文網絡，其中共有2 708篇論文(節點)，5 429對論文之間的引用關系(邊)，分為7個研究領域。每篇論文均用一個0/1值的詞向量描述，該詞向量指示論文中是否存在相應的詞，共包含1 433個單詞,并視為每篇論文的屬性。

Citeseer(https://linqs.soe.ucsc.edu/data)是一個引文網絡數據集。它包含6個研究領域的3 312篇研究論文，含有4 732條邊。每篇論文均用一個0/1值的詞向量描述，該詞向量指示論文中是否存在相應的詞，共包含3 703個單詞,并視為每篇論文的屬性。

人工數據集是使用LFR 基準[15]生成的LFR-1和LFR-2。在人工數據集的每個真實類別中，節點均附有隨機生成的相似屬性，且2個不同類別之間的屬性有差異。LFR參數符號及其含義如表3所示，其具體參數的設置如下所示：

LFR-1:N=20000,k=10,max_k=50,μ=0.1,τ1=2,τ2=1,min_c=20,max_c=50,On=0,Om=0。

4.2 對比算法

為評估本文算法NETA的性能，選取以下2類算法進行對比，第1類算法只考慮網絡拓撲結構而沒有考慮節點的屬性信息，即DeepWalk和node2vec。第2類算法融合了網絡拓撲結構和節點屬性信息，即TADE和DANE。具體描述如下所示：

(1)DeepWalk[6]：通過從每個圖節點開始隨機游走生成節點序列來模擬句子，這一系列節點序列組成了“語料庫”。DeepWalk 設定了背景窗口的大小，然后將隨機游走得到的“語料庫”輸入skip-gram模型，得到每個圖節點的圖嵌入表示。

(2)node2vec[8]：為了挖掘網絡結構的局部特性和全局特性，引入2個超參數p和q控制隨機游走的策略，得到特定的節點序列后也運用skip-gram模型學習節點表示。

(3)TADE[9]：在矩陣分解的框架下，將節點的文本特征引入到網絡表示學習中。

(4)DANE[10]：該算法可以捕捉到結構與屬性的高度非線性關聯，并在拓撲結構和節點屬性上保持近似性特征。

對于DeepWalk和node2vec，窗口大小設置為10，步長為80，步數為10。對于其余的對比算法，其參數設置遵循原始論文，最后將節點表示的維數設置為64。

4.3 實驗結果與分析

4.3.1 節點分類和節點聚類(問題1)

為了驗證本文算法NETA的性能，將NETA得到的節點表示分別用于節點分類和節點聚類任務。在節點分類任務中，采用K近鄰KNN(K-Nearest Neighbor)(K=7)分類器進行節點分類。本文使用Macro-F1和Micro-F1作為評價指標。表4給出了算法運行10次的平均結果。在節點聚類任務中，采用K-Means聚類算法進行節點聚類，將K-Means的簇數設置為每個數據集的類別數，使用歸一化互信息NMI(Normalized Mutual Information)和調整蘭德系數ARI(Adjusted Rand Index)作為評價指標。由于K-Means的性能受初始簇中心的影響，因此將本文算法重復運行10次，并在表5中給出了平均結果。

從表4和表5中可以看出，在節點分類和節點聚類任務中，本文算法的效果相比其他對比算法均為最優。在分類任務中，針對2個數據集而言，TADE、DANE和本文算法NETA均優于DeepWallk和node2vec，這在一定程度上表明，網絡中節點的屬性可以為網絡嵌入提供較好的支持，將網絡拓撲結構和節點屬性信息融合之后，網絡嵌入的效果有了較大提升，這點在表5中也有體現。其次，本文算法NETA在2個數據集上均優于TADE和DANE，這說明捕獲節點的重要性和節點-屬性的重要性對網絡嵌入是有益的，不同的節點在進行嵌入表示時應該有著不同的重要程度。

4.3.2 參數敏感性分析(問題2)

在數據集Cora，Citeseer和LFR-1上對參數的敏感性進行分析，研究不同參數對本文算法NETA的影響。

(1)最終節點嵌入的維度。

本文算法NETA的分類效果受最終的節點嵌入向量z維度的影響。本節在3個不同數據集上對不同維度的節點嵌入向量z進行測試，實驗結果如圖2所示。可以看出，在Cora和Citeseer數據集上，本文算法NETA的性能在維度為64時效果最好，后續隨著維度的繼續增加，NMI值開始降低，算法性能也隨之下降；在LFR-1人工數據集上，當最終嵌入維度為128時，本文算法NETA性能最好，后續同樣隨著維度的增加，算法性能也下降。原因是NETA需要一個合適的維度來編碼信息，更大或者更小的維度可能會使信息不充分或者帶來冗余，導致效果不佳。

(2)語義級注意力向量維度。

語義級注意力的性能受語義級注意力向量的影響，本節在3個不同的數據集上對不同維度的語義級注意力向量進行測試，實驗結果如圖3所示。

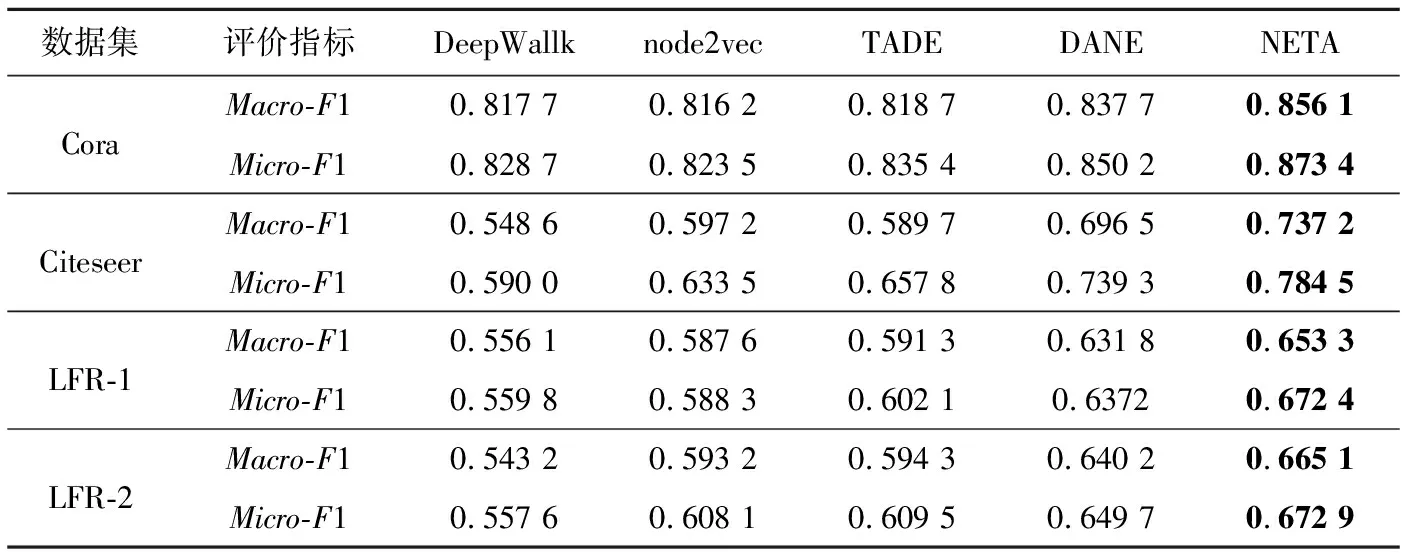
Table 4 Performance comparison of node classification

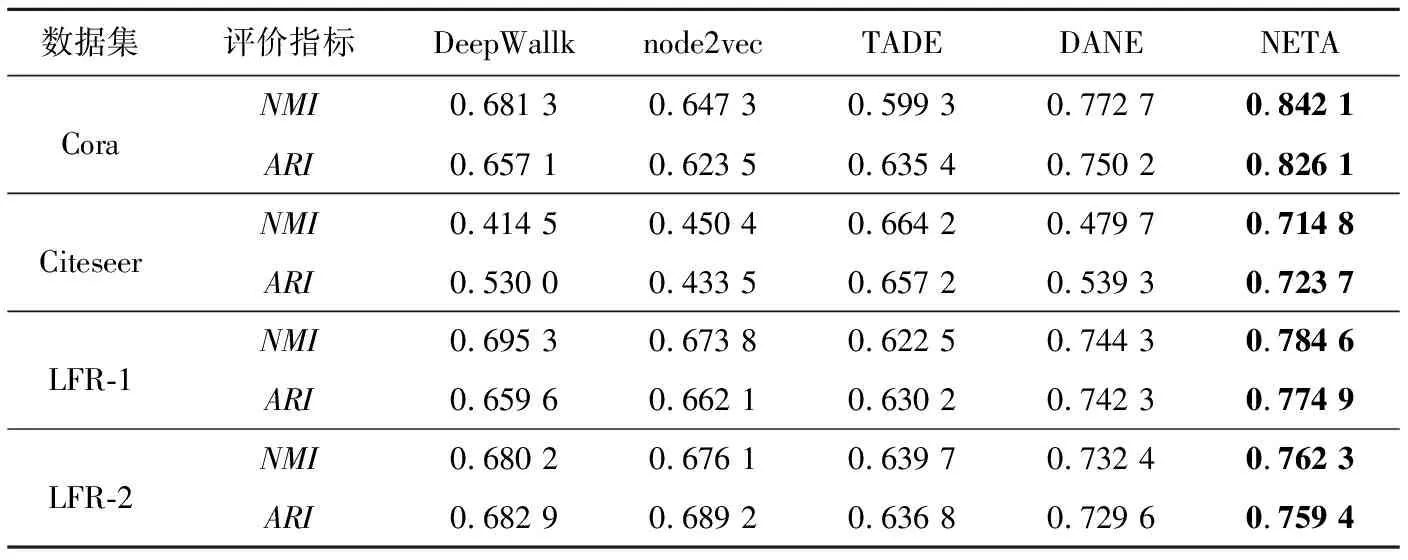
Table 5 Performance comparison of node clustering

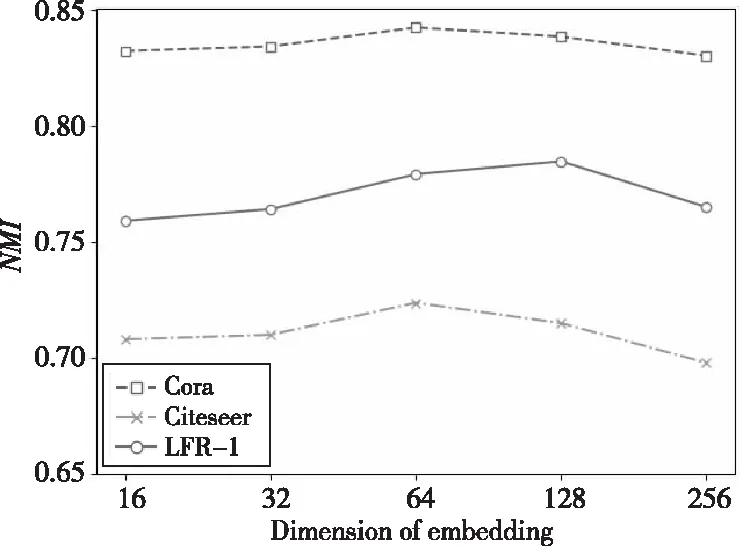
Figure 2 Effect of dimension of embedding on NMI

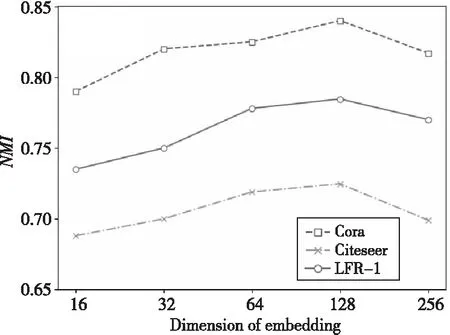
Figure 3 Effect of the semantic-level attention vector dimensionality on NMI

可以看出，在3個數據集上，當注意力向量的維度均在128時，本文算法NETA的性能最好。之后，算法性能開始降低，這可能是由于過擬合引起的。

(3)多頭注意力機制數量。

為測試多頭注意力機制的效果，本節在3個不同的數據集上設置不同K值進行測試，當K=1時多頭注意力機制退化為單頭注意力機制，實驗結果如圖4所示。從圖4中可以看出，隨著K值的增加，本文算法NETA在3個數據集上的性能都得到了提升，當K=8時算法性能達到最好。

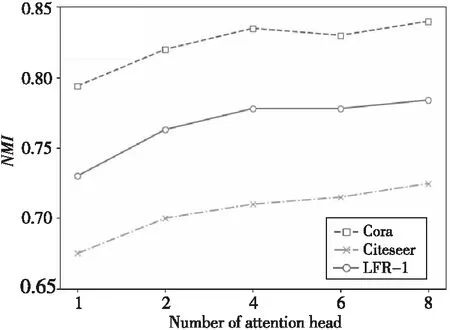
Figure 4 Effect of number of multiple attention mechanism on NMI

4.3.3 注意力機制分析(問題3)

在學習節點的嵌入表示時，本文考慮了不同類型的鄰居及其重要性，并為其分配了不用的權重。為了更好地理解權重的意義，本節設計案例對節點級注意力和語義級注意力進行分析。

(1)節點級注意力機制。

以Cora數據集為例，將節點P2583及其鄰居表示為圖5，它們的注意力權重如圖6所示。P2853、P1423和P2135表示神經網絡領域的論文；P378和P1173表示概率方法領域的論文；P2337表示基于案例領域的論文。從圖6可以看到，表示神經網絡領域論文的節點的鄰居節點權重較大，其他領域論文的節點的鄰居節點權重較小。其中，節點P2583在節點級上有著最大的注意力權重，這說明節點本身在嵌入中起著最重要的作用。這是合理的，因為表示一個節點，最重要的是節點自身的信息，而通常將鄰居的信息視為一種補充信息。此外，節點P1423和P2135有著第2和第3的注意力權重，因為它們也表示神經網絡領域的論文，可以為識別P2583的類別做出重要貢獻。其余鄰居的注意力權重較小，因為它們所表示的論文不屬于神經網絡領域并且不能很好地為識別P2583做出一定的貢獻。根據上述分析，可以看到節點級的注意力權重可以區分鄰居之間的重要程度，并為一些有意義的節點分配較高的權重。

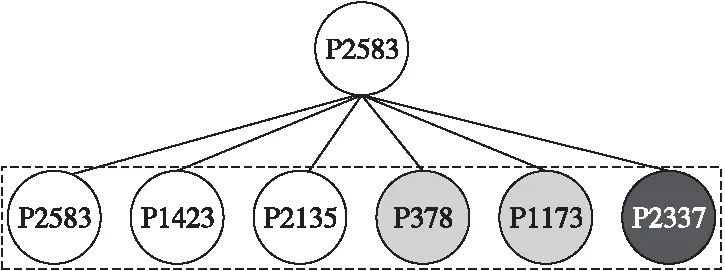
Figure 5 Neighbors of P2583 in topology

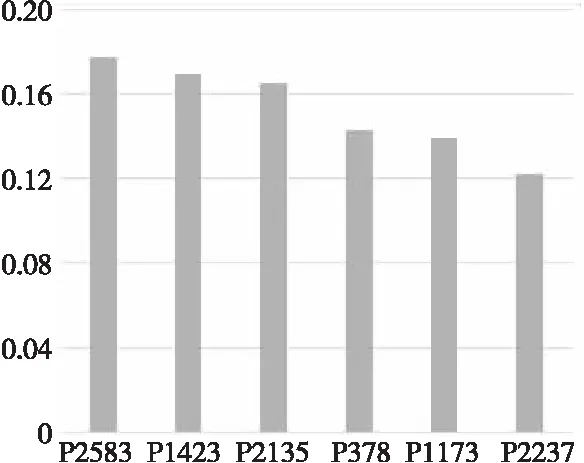
Figure 6 Weight distribution of neighbors of P2583

(2)語義級注意力機制。

為了分析鄰居類型對節點表示的重要性，本文對比了僅使用某一種鄰居類型進行節點表示的結果及該鄰居類型的注意力權重，結果如圖7所示。從圖7中可以看出，僅考慮單獨鄰居類型的節點表示結果與該鄰居類型的注意力權重成正比，由此可見，本文算法能夠較好地學習到不同鄰居類型對節點表示的重要性。

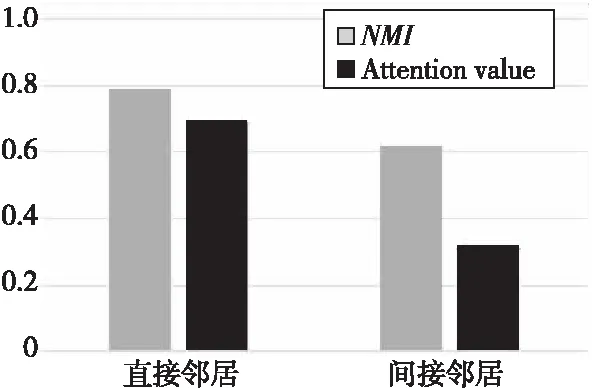
Figure 7 Attention weight of two types of neighbors

4.3.4 注意力機制消融分析(問題3)

為了分析節點級注意力和語義級注意力對本文算法的貢獻，本節設計了該算法的2種變體。首先變體1僅考慮語義級注意力(NETA-N)，并為每個節點的鄰居分配相同的權重；變體2僅考慮節點級注意力(NETA-S)，并認為拓撲結構和結構-屬性二部圖的重要程度相同，最后以本文算法NETA為基準，在Cora數據集上分別進行了節點分類和節點聚類任務，表6為3種算法執行10次的平均結果。

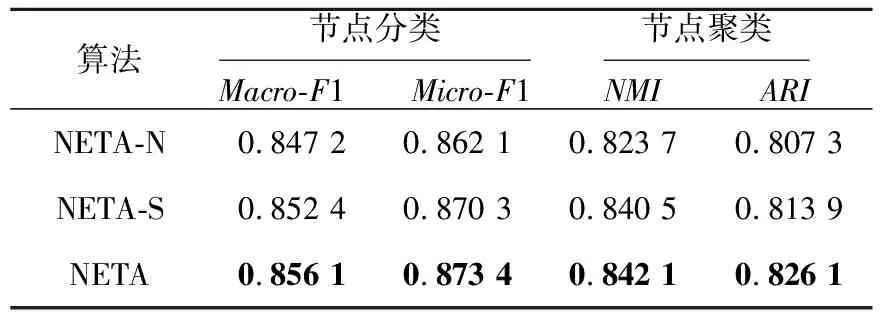
Table 6 Performance comparison of NETA and variants

從表6中可以看出，首先，不考慮節點級注意力(NETA-N)或者不考慮語義級注意力(NETA-S)時，性能都比基準算法NETA差，這說明對節點級注意力和語義級注意力建模是很有必要的。其次，通過比較NETA-N和NETA-S可以得知，在不考慮節點級注意力時本文算法性能下降比不考慮語義級別時算法性能下降要多一些，這說明節點級注意力相比語義級注意力更加重要，因為節點級注意力對節點的鄰居根據重要程度分配不同的權重，其包含的信息更加有助于節點的表示。

5 結束語

本文設計了一種融合雙層注意力機制的節點嵌入算法來有效實現屬性網絡的嵌入。首先將節點的直接鄰居和間接鄰居利用注意力機制進行表示；然后聚合直接鄰居的重要性和間接鄰居的重要性以生成節點的最終嵌入。在真實數據集上的大量實驗驗證了本文算法NETA的有效性。但是，在構建結構-屬性二部圖時，本文僅考慮了節點間是否擁有相同屬性，并未考慮節點擁有相同屬性的數量。其次，在結構-屬性二部圖上進行的跳轉僅考慮了鄰居節點對嵌入的貢獻，并未考慮中間節點的影響，這將是下一步需要研究的問題。