依美構造數列,提升運算素養
俞文銳
(福建省福清華僑中學 350300)
求數列通項的方法有直接利用等差、等比公式求通項,用累加法、累乘法、待定系數法求通項,構造等差、等比數列求通項,還有利用遞推公式求通項.面對如此多的題型和方法,學生顯得無所適從.美無處不在,那么我們能否運用數學美將復雜數列進行變形,從而構造出特殊數列予以求解呢?下面以近年高考試題為例,設計數學美問題情境,以期提升學生的數學運算核心素養.
1 明晰運算對象,確定運算起點
數學運算是指在明晰運算對象的基礎上,依據運算法則解決數學問題的素養.[1]7數學運算核心素養的水平一指出:能夠在熟悉的數學情境中了解運算對象,提出運算問題.[1]105由此可知明晰運算對象是展開數學運算的先決條件,教師要引導學生在熟悉的問題情境中,從不同角度進行觀察,選擇不同的運算對象,確定運算起點.
例1(2022年高考全國乙卷數學文科第13題)記Sn為等差數列{an}的前n項和.若2S3=3S2+6,則公差d=.
分析本題可以利用基本量方法進行求解,即將已知條件轉化為d的方程.由2S3=3S2+6,得2(3a1+3d)=3(2a1+d)+6,解得d=2.
教學不應該停留于解題本身,要充分挖掘高考試題的教學價值,為此可做如下設計:
問題1 能否從題設Sn的表達式中提取出其他的信息?
問題2 能否根據統一美構造出與Sn有關的新數列?
問題3 能否利用新數列的信息求d?
通過問題1,引領學生從數量關系中抽象出運算對象,即關注Sn,發現S3與S2的系數分別為2和3,下標與系數對換,給人一種不統一的感覺.
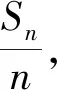
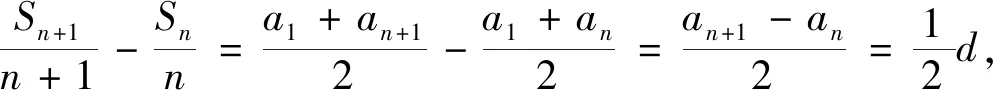
在上述的活動中,學生經歷了從數量關系中抽象出運算對象、從數學美的角度構造運算對象、根據運算對象確定運算起點的認知過程,從中使得數學抽象、數學運算等核心素養獲得提升.
2 探索運算思路,把握知識本質
數學運算核心素養水平一要求:能夠在熟悉的數學情境中,根據問題的特征形成合適的運算思路,解決問題.[1]105數學運算不是盲目的,往往需要學生觀察數與式的結構特征,展開豐富的聯想,通過合理的構造,進行嚴謹的邏輯推理,獲得合適的運算思路.
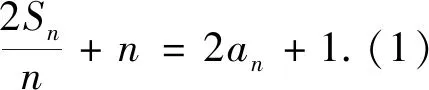
分析本題已知條件中Sn與an糾纏,要研究an必須消去一個變量,為此可做如下設計:
問題1 能否根據簡潔美對已知條件進行化簡并獲得Sn的表達式?
問題2 能否根據對稱美對化簡的結果進行變形?
問題3 能否構造出新數列,并利用新數列對原問題進行求解?

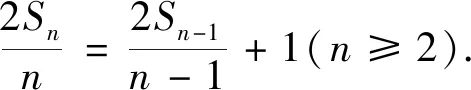
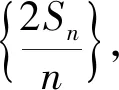
3 選擇運算方法,完善學生認知
數學運算的核心是思維,解題中應強化對運算思路和方法的分析,使學生逐步理解運算是一種邏輯推理,在面對與學過的知識有關聯的數學命題時,能夠通過對其條件與結論的分析,探索運算的思路,選擇合適的運算方法,體會程序思想的意義和作用.
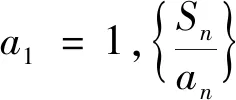
本題的問題情境對學生而言不熟悉,基于高考考查目標要求,結合必備知識和關鍵能力設計如下問題:
問題1 能否根據等差數列的定義獲得Sn與an的關系式?
問題2 能否將關系式中的Sn轉化為an?
問題3 能否構造出與an有關的新數列?
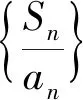
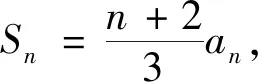
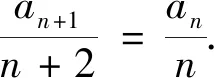
在上述的活動中,學生對于較復雜的數學問題,能夠通過結構與變量的和諧統一美,對式子進行變形構造,得到完美統一的關系式,從而得到常數列.該活動讓學生進一步認識到數學美的威力,促進學生將新知識同化到已有的數學認知結構中,從而使數學認知結構得到進一步的發展.
4 變換運算背景,累積活動經驗
數學運算核心素養和數學思維的提升不能僅僅滿足于熟悉情境下的模仿與記憶,為了提高學生在綜合情境中把問題轉化為運算問題的能力,教師需要不斷變換運算背景,提高學生的應變能力.
例4(2021八省聯考第17題)已知各項均為正數的數列{an}滿足an+2=2an+1+3an.
(1)證明數列{an+an+1}為等比數列;
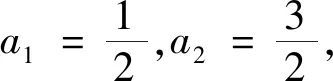
分析 (1)略;
(2)由(1)得an+an+1=2·3n-1,根據求通項公式的經驗,移項得an+1=-an+2·3n-1,此時發現an+1,an的系數不含n,還能通過適當的變形化成對稱統一的結構嗎?

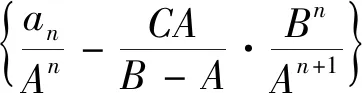
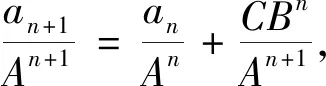

在上述的活動中,學生從綜合的運算背景中,能夠通過構建過渡性的命題,探索論證的途徑,解決問題,并會用嚴謹的數學語言表達論證過程,感悟數學之美,積累依美構造數列的經驗.
5 結語
依美理解運算對象,依美探究運算思路,依美選擇運算方法,依美求得運算結果,學生在教師設置的問題情境中,感受到數列通項求解過程中結構變量的對稱美、統一美,自覺地用美來解決遞推數列問題,從而實現數學美在遞推數列問題中的知行合一,同時累積了求解遞推數列通項公式的基本活動經驗,學會用美的眼光看問題,培養和發展數學運算核心素養.

