基于夾點理論的人工冰場CO2制冷熱回收系統優化分析

周嘯虎 耿旭東 李 鋒 司春強 馬 進 邵雙全

（1 華中科技大學能源與動力工程學院 武漢 430074；2 華商國際工程有限公司 北京 100069）

近年來，環境問題已逐漸成為全球關注的焦點之一，而我國作為當今最大的碳排放國家一直致力于減少氫氟烴的排放以及尋找清潔能源[1]。制冷行業作為制造業中的重要組成部分，能耗高，節能減排的潛力巨大。其中，人工冰場是能耗較高的建筑之一[2]。因此，降低人工冰場能耗能極大促進節能減排的實現，關鍵在于換用節能環保的制冷劑和采用高效的制冷系統配置。CO2作為自然工質，具有安全性、環保性、優越的熱力學性能等優點[3]，逐漸受到人們的廣泛關注，并應用于熱泵[4]、汽車空調[5]、超市[6]、冷藏車[7]等領域。自1999年建造了第一個使用CO2作為載冷劑的人工冰場[8]以來，CO2也開始被用于人工冰場行業。雖然優點眾多，CO2仍存在臨界溫度較低的問題。當環境溫度較高時，CO2制冷系統處于跨臨界循環運行時的效率較低[9]。因此，許多研究致力于提高CO2制冷系統的性能，如使用熱電過冷[10]和機械過冷[11]增加過冷度，使用多級壓縮[12]和并行壓縮[13]降低壓縮機功耗，使用渦管[14]、膨脹機[15]和噴射器[16]代替膨脹閥減少節流損失。因此，本文采用噴射器和并行壓縮同時改進的系統應用于人工冰場進行分析。

人工冰場除了常規的制冷需要，還有較多制熱需求，包括生活熱水、除濕再生、通風供暖等[17]，而CO2高熱回收潛力剛好可以滿足人工冰場的部分甚至全部需求。因此人工冰場的CO2制冷熱回收系統相當于制冷及熱泵系統進行結合，可極大降低能耗。

但超臨界狀態下的CO2在換熱時會出現溫度滑移，導致水冷式換熱器產生夾點，從而限制換熱性能及出水溫度[18]。熱泵系統中傳統的熱力學分析中常以固定氣冷器出口溫度模型來計算系統性能（本系統中應為固定熱回收換熱器CO2出口溫度），從而忽略了夾點的影響。因此，Chen Yunguang[19-20]使用夾點分析法對CO2熱泵熱水器進行熱力學分析，得出有關參數對系統換熱的影響規律，并分析夾點對CO2熱泵最佳排熱壓力的影響。

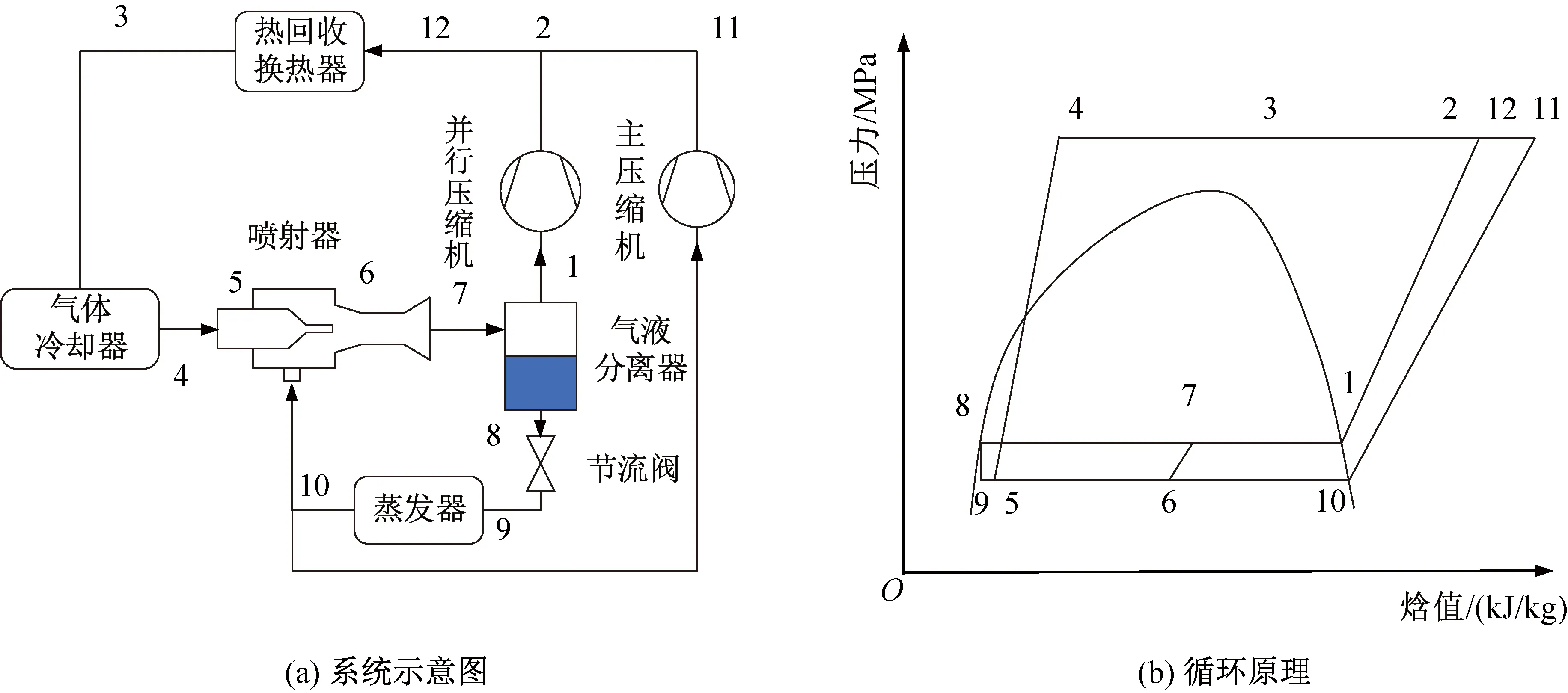
圖1 并行壓縮噴射制冷系統Fig.1 Parallel compression ejector expansion refrigeration cycle

因此，以人工冰場改進的CO2制冷熱回收系統為背景，基于夾點分析理論，本文對人工冰場CO2制冷熱回收系統進行了優化分析，并與理論計算結果進行對比，得到夾點對該系統有關參數及性能的影響，從而更好的指導熱回收的控制以提升系統性能。

1 人工冰場CO2制冷熱回收系統模型建立

1.1 循環描述

本文人工冰場CO2制冷熱回收系統為并行壓縮噴射制冷系統（parallel compression ejector expansion refrigeration cycle，PCEERC），系統示意圖和循環原理如圖1所示。該系統循環包括兩個壓縮機、氣體冷卻器、氣液分離器、節流閥、蒸發器、熱回收換熱器和噴射器。循環工作原理如下：主壓縮機和并行壓縮機出口的制冷劑混合（狀態12），經過熱回收熱交換器（在單獨制冷模式下，熱回收熱交換器將旁通）和氣體冷卻器冷卻（冷凝器）（狀態4），進入噴射器的主噴嘴中膨脹加速（狀態5），并引射來自蒸發器的部分流體（狀態10）。然后兩種流體在混合室內恒壓混合（狀態6），在擴散器中擴散，其中動能轉換為壓力勢能（狀態7）。最后，將兩相流體從噴射器排出，進入氣液分離器，分離成飽和液體（狀態8）和氣體（狀態1）。其中，飽和液體進入節流閥節流成低壓流體（狀態9），然后進入蒸發器。而飽和氣體通過并行壓縮機進行壓縮（狀態2）。同時，來自蒸發器出口流體的另一部分進入主壓縮機（狀態11），主壓縮機與來自平行壓縮機的流體混合并繼續循環。

1.2 熱力學模型

本文從質量、動量和能量守恒的角度對循環的每個過程進行能量分析，從而建立熱力學模型，其中噴射器采用一維恒壓混合模型。

為簡化熱力學模型，進行如下假設：

1）所有部件均處于穩態運行，流體在噴射器中處于一維流動；

2）氣液分離器和蒸發器出口均為飽和流體，制冷劑在膨脹閥節流前后焓值相等；

3）管道中的壓降和熱、流量損失均忽略不計；

4）混合過程發生在混合室中，恒壓等于蒸發壓力，噴射器進出口處的速度忽略不計；

5）在噴射器中，噴嘴效率ηn為0.8，混合效率ηm為0.95，擴散效率ηd為0.8[21]；

6）制冷量Q0為20 kW，蒸發溫度Te為-20 ℃，若無特殊說明，蒸發器出口的兩股流體質量流量比為1；

7）假設兩級串聯熱回收，低溫級進、出口水溫為40 ℃和60 ℃，高溫級為60 ℃和80 ℃；

8）壓縮機最高排氣溫度為160 ℃，最高排氣壓力為11 MPa；

9）假設環境溫度為35 ℃，換熱器的夾點溫差為3 ℃，因此氣冷器出口溫度為38 ℃；理論的熱回收換熱器出口溫度T3為43 ℃。

噴射器的引射系數μ：

（1）

式中：m10，e為蒸發器出口流向噴射器的二次流體質量流量，kg/s。

設蒸發器出口流向壓縮機的流體與流向噴射器的流體的質量流量之比β為：

（2）

式中：m10,c為蒸發器流向壓縮機流體的質量流量，kg/s。

壓縮機的等熵效率ηcom：

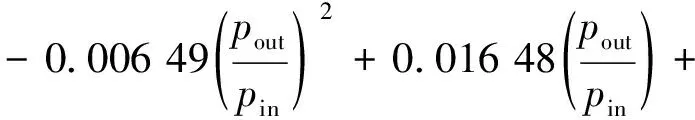
0.664 6

（3）

蒸發器處的制冷劑質量流量m10：

（4）

結合μ和β可求得其它部件的質量流量（包括m10,e、m1、m4），主壓縮機、并行壓縮機及總功耗為：

W10,com=m10,e（h11-h10）

（5）

W1,com=m1（h2-h1）

（6）

W=W10,com+W1,com

（7）

熱回收量：

Qhr=m4（h12-h3）

（8）

系統的制冷性能系數、制熱性能系數以及綜合性能系數為：

（9）

（10）

（11）

2 夾點分析計算模型

圖2所示為兩級串聯熱回收的換熱情況。

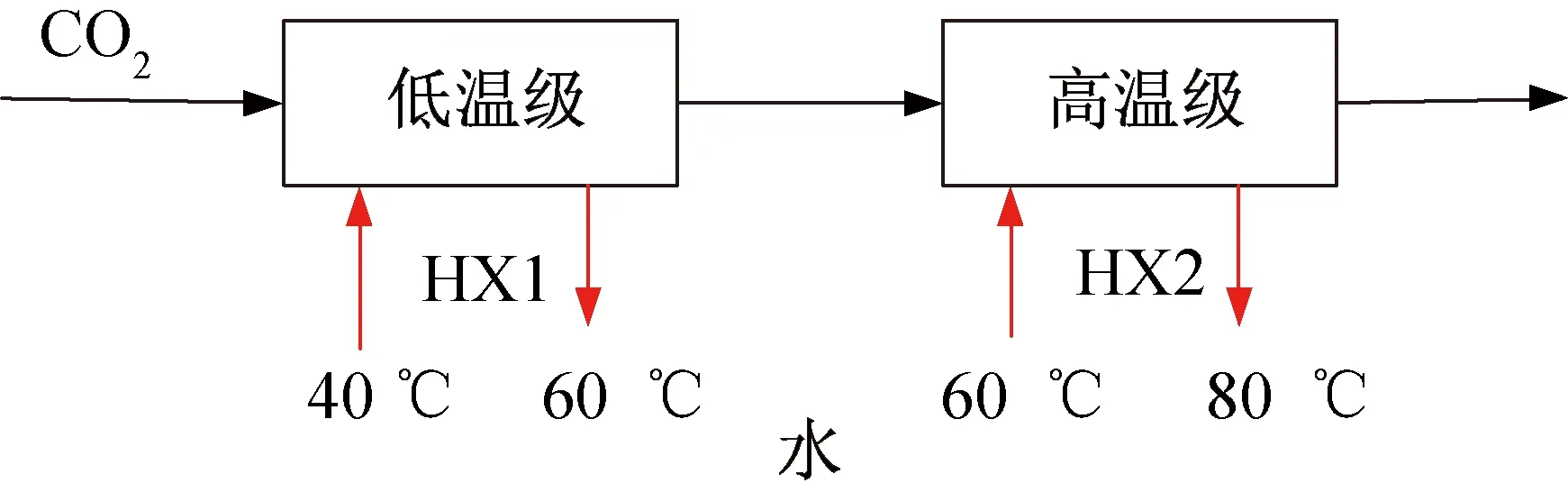
圖2 兩級熱回收示意圖Fig.2 Schematic diagram of two-stage heat recovery

理論情況下熱回收換熱器CO2出口溫度T4為43 ℃，實際上由于夾點的限制，熱回收換熱器的出口CO2溫度一般高于43 ℃，從而影響熱回收量和制熱性能系數甚至綜合COP，但對制冷性能系數并無影響，因此后續性能分析不包括制冷性能系數。在本文假設工況下（進出口水溫固定），可通過調節高低溫級的水質量流量來改變夾點的位置從而調節T4，本文采用的分析方法為T-Q圖分析，如圖3所示，圖中換熱曲線的斜率為熱容（比熱容乘以質量流量）的倒數，不同取水段的進出口水溫順接。可以看出高低溫的水質量流量變化會影響T4。

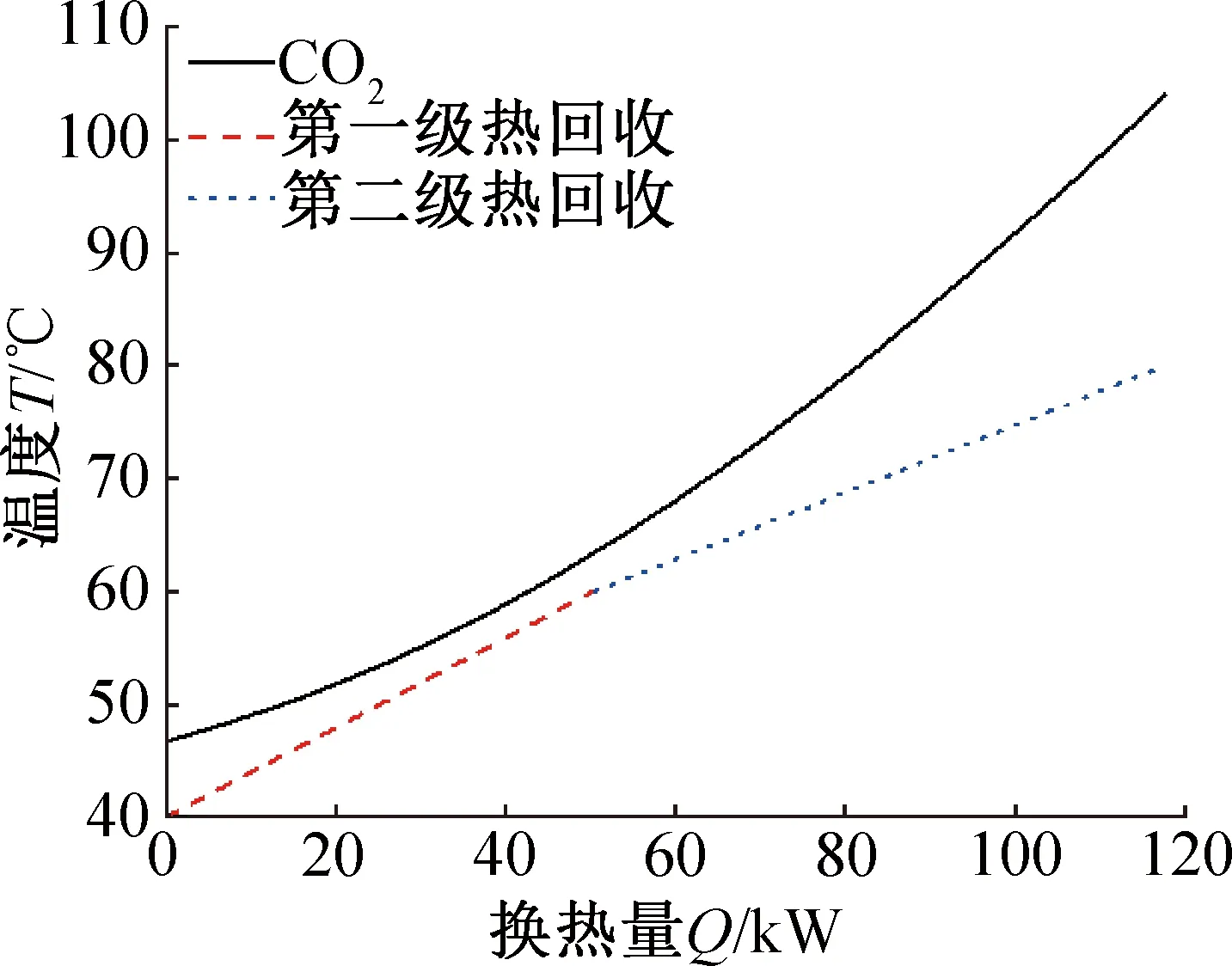
圖3 T-Q圖Fig.3 T-Q figure

在不同排氣壓力下，CO2換熱曲線中的近臨界點和近臨界溫度也是主要影響因素。圖4所示為不同排氣壓力下CO2比熱容隨溫度和壓力的變化。可以看出，排氣壓力越高，除整體熱容降低外，熱容的最高峰對應的溫度（近臨界溫度）越大，當排氣壓力由7.5 MPa增至11 MPa，近臨界點溫度由32 ℃升至約50 ℃。

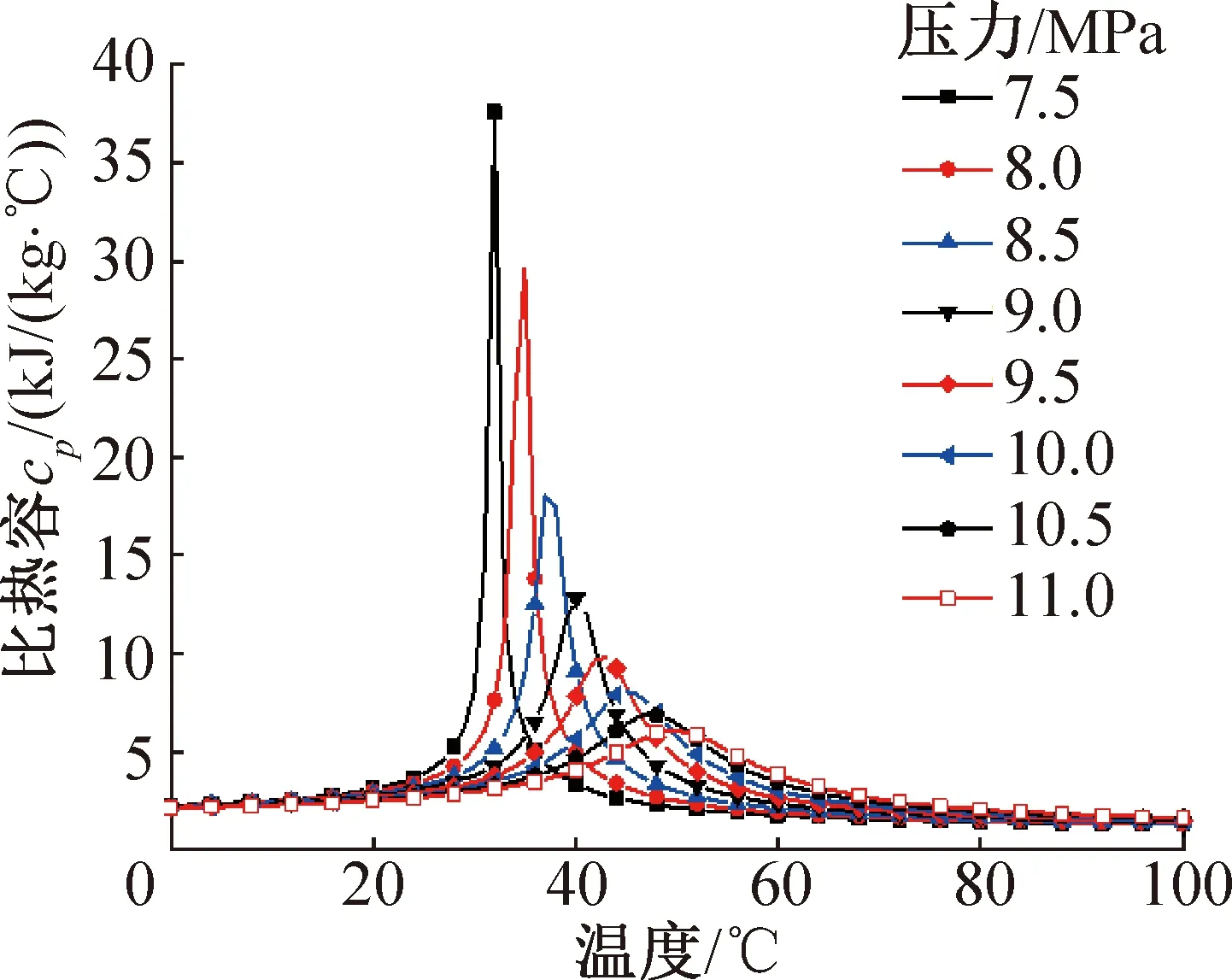
圖4 CO2比熱容隨溫度和壓力的變化Fig.4 Specific heat capacity of CO2 varies with temperature and pressure

為了更好地分析不同進水質量流量或水與CO2的質量流量比對夾點的影響，以及對整體系統循環性能的影響，此時并不固定制熱量，主要分析水與CO2的質量流量比對CO2出口溫度及整個系統的影響。計算方法為：假設某一級質量流量比漸變時，另一級的質量流量比對應以盡量減小CO2出口溫度為優化目標進行選取。

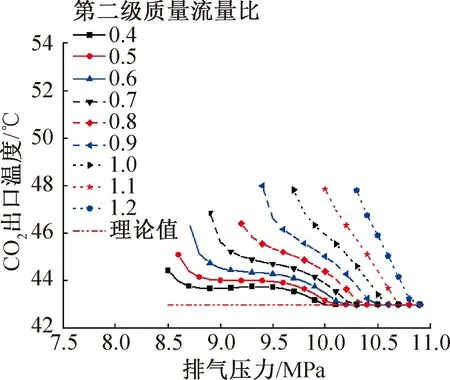
圖5 不同第二級質量流量比下CO2出口溫度隨排氣壓力的變化Fig.5 Variation of CO2 outlet temperature with discharge pressure under different second stage mass flow ratio

3 結果與分析

3.1 第二級質量流量比漸變

圖5所示為不同排氣壓力和第二級質量流量比的CO2出口溫度變化。可以看出，當第二級質量流量比越大時，高溫級換熱區域溫度滑移匹配越差，因此需要通過提升排氣壓力來提高CO2的進口溫度，從而滿足80 ℃的供水溫度，即能夠開始進行熱回收所需的排氣壓力會越高。

同時，在剛好能進行熱回收的排氣壓力下時，質量流量比越大，CO2出口的溫度整體均升高，說明當第二級熱回收處的溫差較小時（夾點出現在第二級熱回收），第二級熱容的不匹配程度也會影響第一級的熱容匹配，從而使CO2出口溫度無法有效降低；而在排氣壓力逐漸升高之后，多數質量流量比下的CO2出口溫度均趨于理論值，說明當第二級熱回收的溫差較大時（夾點不在第二級熱回收處），第二級質量流量比對第一級的熱容匹配的影響很小，第二級的質量流量比基本均能調節使CO2出口溫度為理論最佳值。

圖6所示為第一級質量流量比隨第二級質量比和排氣壓力的變化。可以看出，第一級質量流量比隨排氣壓力的升高和第二級質量流量比的降低而增大。當排氣壓力升高時，需要升高第一級質量流量比來降低CO2出口溫度。

圖6 不同第二級質量流量比下第一級質量流量比隨排氣壓力的變化Fig.6 Variation of first stage mass flow ratio with discharge pressure under different second stage mass flow ratio

由于CO2出口溫度受到影響，使制熱性能系數和綜合性能系數均受影響。

圖7所示為熱回收量的變化情況，理論情況下，熱回收量會隨排氣壓力的升高先降低再升高，但考慮夾點時，排氣壓力升高會使CO2出口溫度降低，導致熱回收單位焓差升高，給熱回收帶來一定的增益，該增益在低排氣壓力下更顯著（此時升高排氣壓力會使CO2出口溫度顯著降低），因此本應降低的熱回收量此時也升高了，導致在某一質量流量比下的熱回收量只會隨排氣壓力的升高而升高。總體而言，第二級質量流量比越大，熱回收量越小。

圖7 不同第二級質量流量比下熱回收量隨排氣壓力的變化Fig.7 Variation of heat recovery with discharge pressure under different second stage mass flow ratio

圖8所示為制熱COP的變化情況。可以看出，變化趨勢與熱回收量基本一致，第二級質量流量比越大時，制熱COP越小，區別是，隨著第二級質量流量比升高，初始可熱回收排氣壓力升高，初始可進行熱回收下的制熱COP也呈先減再增的趨勢，與熱回收量先減后增的趨勢相同，但程度更輕，原因是壓縮機功耗會先減后增。

圖8 不同第二級質量流量比下制熱COP隨排氣壓力的變化Fig.8 Variation of heat coefficient of performance with discharge pressure under different second stage mass flow ratio

圖9所示為綜合COP的變化情況，前期COP在不同質量流量比下相等的原因是沒有熱回收，COP即制冷性能系數，而不同質量流量所影響的CO2熱回收出口溫度對制冷性能系數并無影響。隨著第二級質量流量比的升高，一方面初始可熱回收對應的排氣壓力下的COP升高，且整體COP均降低；隨著第二級質量流量比的升高，最大COP對應的最佳排氣壓力也向后移動，超過限制的最大排氣壓力。理論情況下，最大綜合COP為3.538，對應的排氣壓力為10.2 MPa，在夾點的影響下，當第二級質量流量比為0.4時，因在10.2 MPa下的CO2出口溫度仍能優化達到43 ℃，此時最佳排氣壓力和最大綜合COP與理論值一致；而當第二級質量流量比為1.2時，由于CO2出口溫度無法得到有效降低，此時最佳排氣壓力成為受限下的最大值10.9 MPa（11 MPa時，壓縮機排氣溫度超出上限），最大綜合COP僅為3.496。

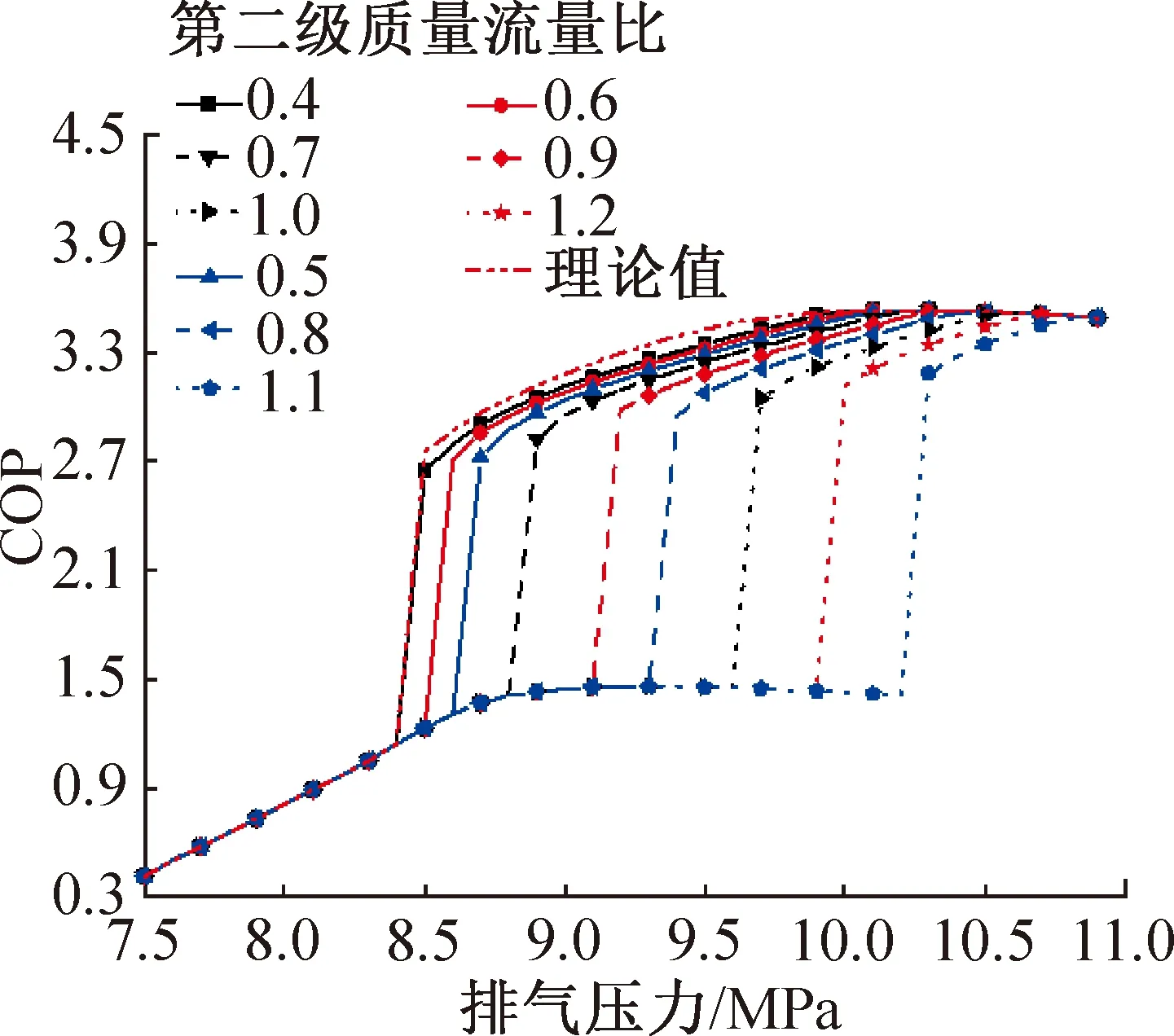
圖9 不同第二級質量流量比下綜合COP隨排氣壓力的變化Fig.9 Variation of comprehensive coefficient of performance with discharge pressure under different second stage mass flow ratio

綜上可知，在第二級質量比漸變，調節第一級質量流量比使CO2出口溫度最低的情況下，第二級質量流量比越大，對系統性能的損害越大，使CO2出口溫度升高，熱回收量、制熱COP和COP降低，并縮小了循環進行熱回收運行的壓力范圍。當第二級質量流量比為1.2時，對應于最大綜合COP的排氣壓力由10.2 MPa移至10.9 MPa，最大綜合COP由3.538降至3.496。

3.2 第一級質量流量比漸變

圖10所示為CO2出口溫度的變化情況。可知，第一級質量流量比越大，溫度滑移匹配越好，CO2出口溫度越低。當第一級質量流量比較小時，CO2出口溫度隨排氣壓力的升高而增大。原因是第一級熱回收溫度滑移匹配較差，第一級熱回收的夾點基本均出現在最右端，而隨著排氣壓力的升高，CO2換熱曲線在T-Q圖上整體均上移，使CO2出口溫度也隨之升高。

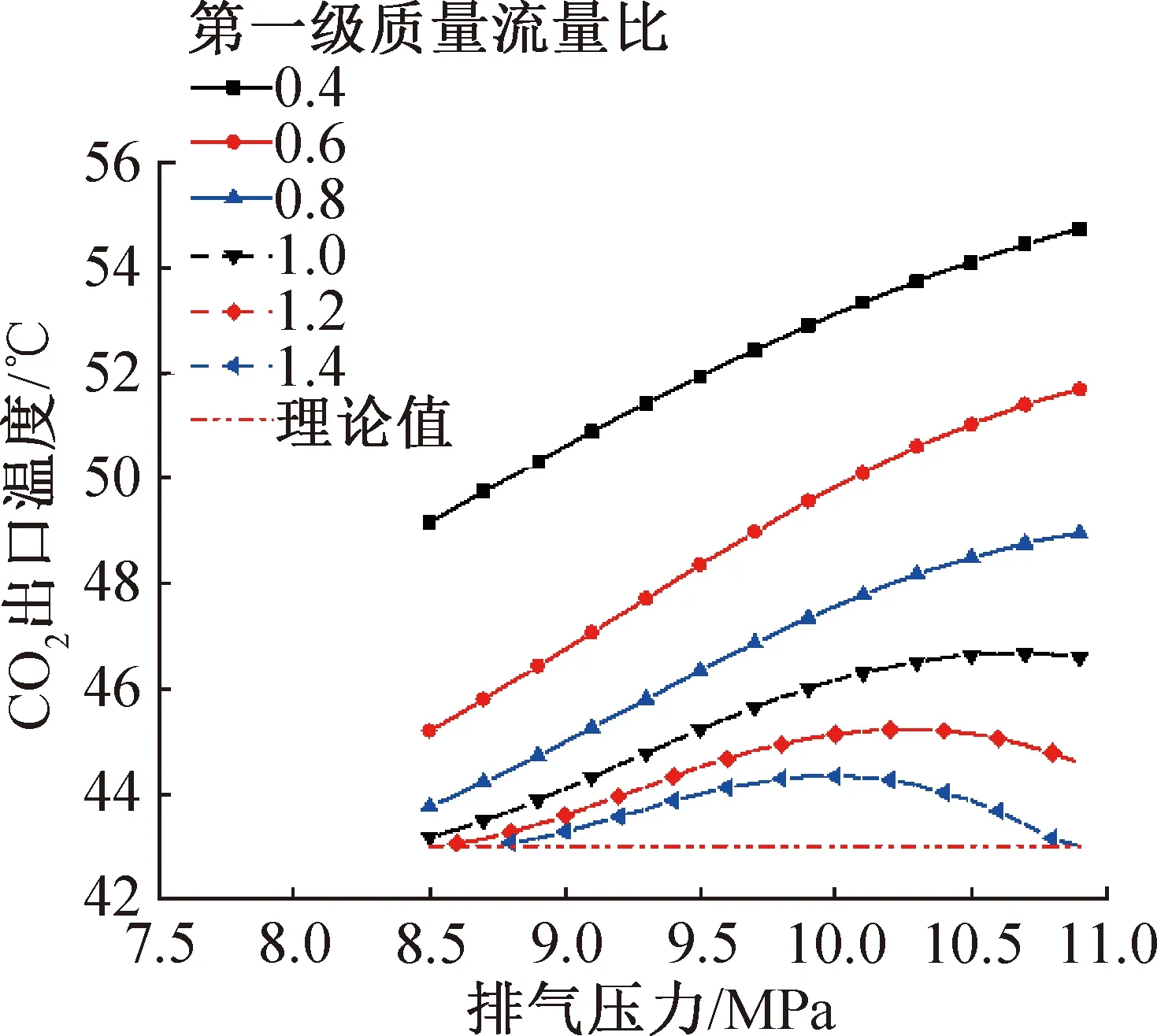
圖10 不同第一級質量流量比下CO2出口溫度隨排氣壓力的變化Fig.10 Variation of CO2 outlet temperature with discharge pressure under different first stage mass flow ratio

當質量流量比升高后，CO2出口溫度隨排氣壓力的升高先增大后減小。原因是此時低溫級整體的溫度滑移匹配較好（整體傳熱溫差較小），第一級熱回收的夾點位置受排氣壓力的影響，在低排氣壓力時，近臨界點溫度較低，此時夾點出現在低溫級熱回收最左端，故此時CO2出口溫度達到最小值，而隨著排氣壓力升高，近臨界點溫度升高，夾點向第一級的中間移動，使CO2出口溫度升高，排氣壓力繼續升高，此時低溫級換熱區域又開始逐漸橫跨CO2換熱曲線的近臨界點左右側，使夾點同時出現在低溫級熱回收的左右側，CO2出口溫度又開始降低，直至理論值。

綜上所述，不同的質量流量比會影響CO2出口溫度隨排氣壓力的變化趨勢,質量流量比越大，整體CO2出口溫度變小。

圖11所示為相應第二級質量流量比的變化情況。第二級質量流量比隨排氣壓力的升高和第一級質量流量比的降低而升高。對應圖10可知，若需降低CO2出口溫度，則需降低排氣壓力，升高第一級質量流量比，降低第二級質量流量比。

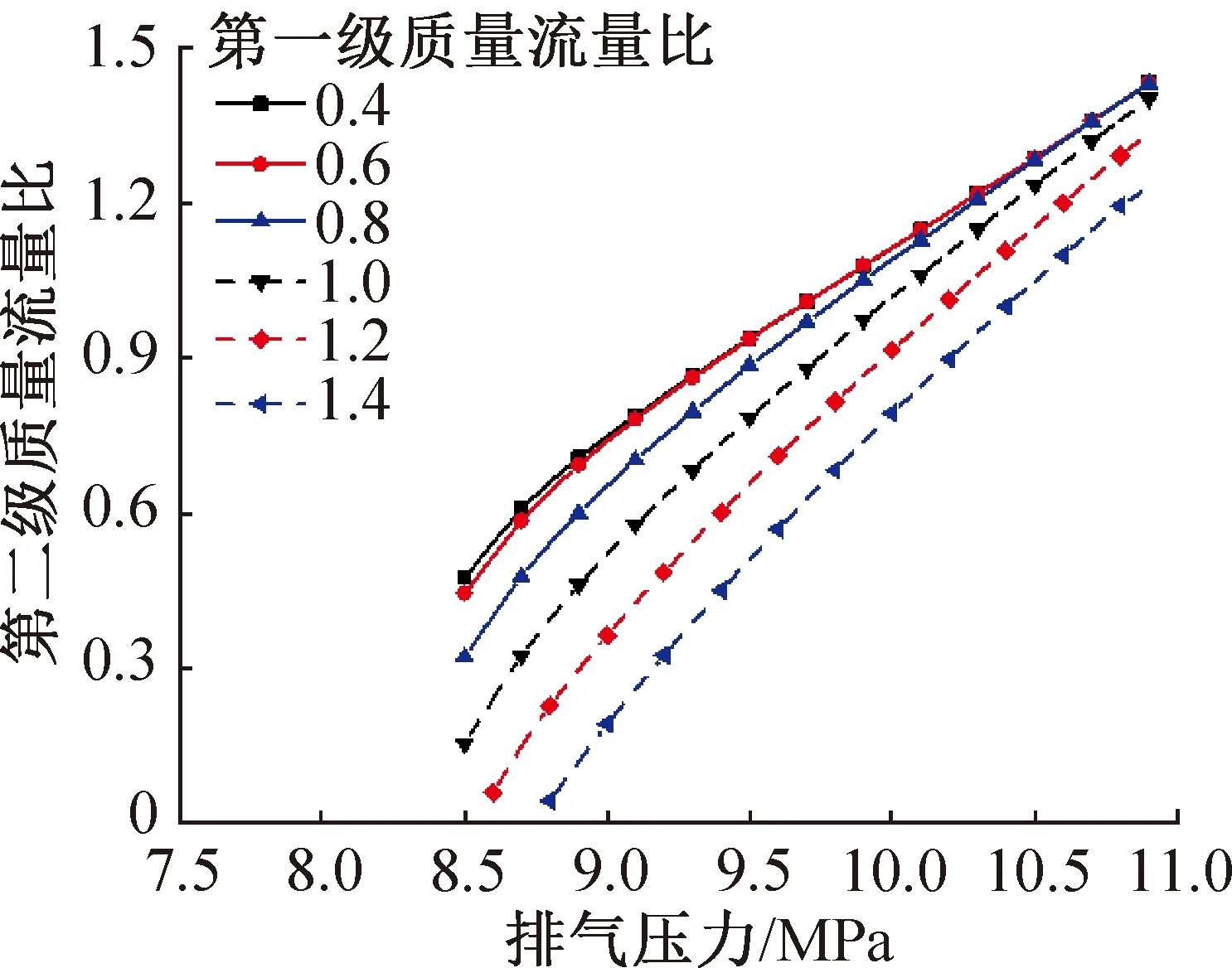
圖11 不同第一級質量流量比下第二級質量流量比隨排氣壓力的變化Fig.11 Variation of second stage mass flow ratio with discharge pressure under different first stage mass flow ratio

圖12所示為熱回收量的變化情況。與理論情況下CO2出口溫度不隨排氣壓力變化不同，當質量流量較小時，CO2出口溫度會隨排氣壓力的升高而升高，導致熱回收的單位焓差變小，熱回收量在理論值的基礎上有所降低，因此在后半段，低質量流量比下的升高趨勢明顯變緩，而高質量流量比下因CO2出口溫度降低，使變化趨勢反而變陡。

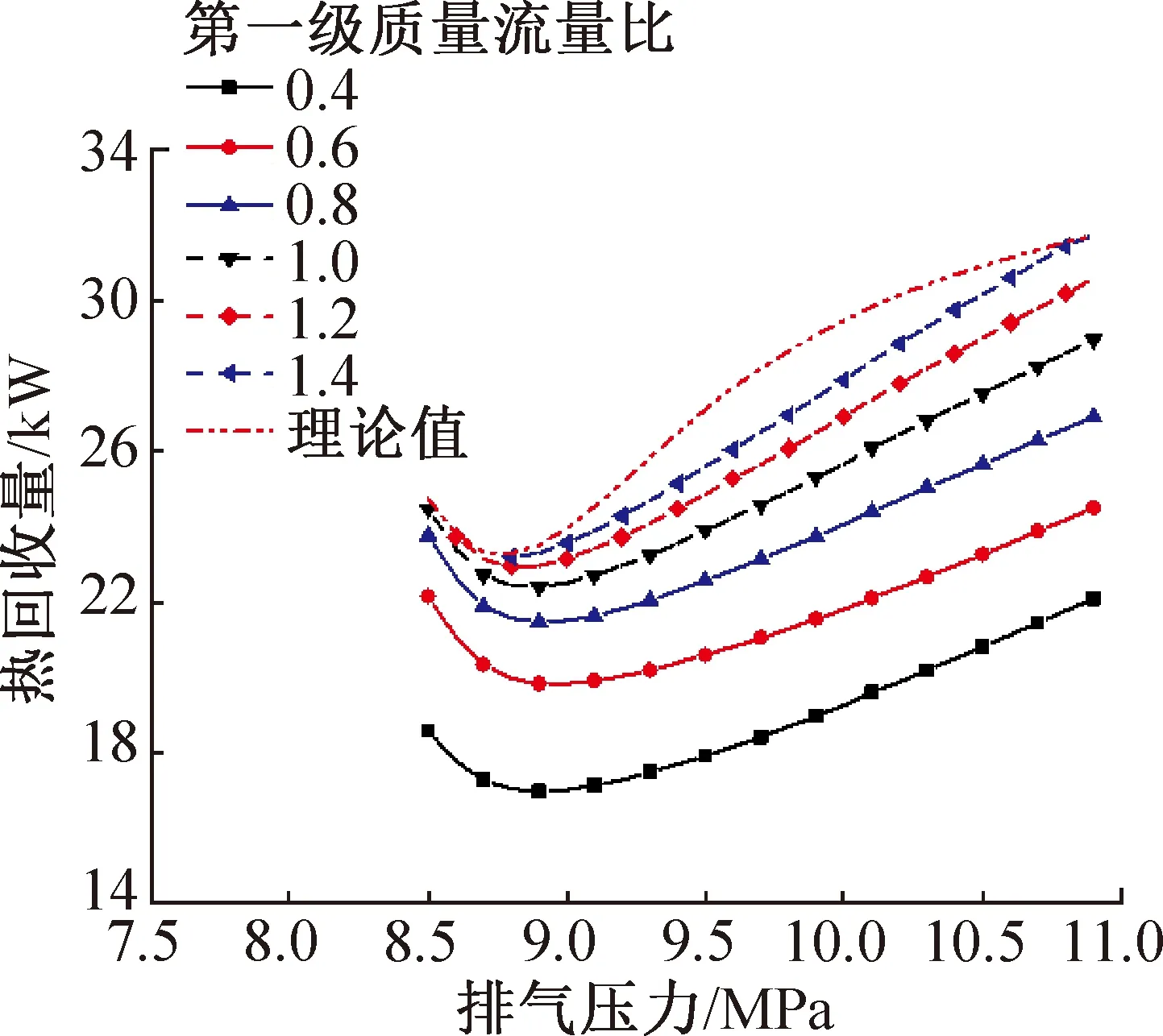
圖12 不同第一級質量流量比下熱回收量隨排氣壓力的變化Fig.12 Variation of heat recovery with discharge pressure under different first stage mass flow ratio

前半段趨勢基本沒變化主要原因是此時質量流量相對較大，單位焓差變化的影響較小。總體而言，質量流量比越大，熱回收量越大。

圖13所示為不同第一級質量流量比下，制熱性能系數隨排氣壓力變化。可以看出，前半段升高趨勢變緩，后半段升高趨勢因質量流量比的不同而變化，與前文分析一致。

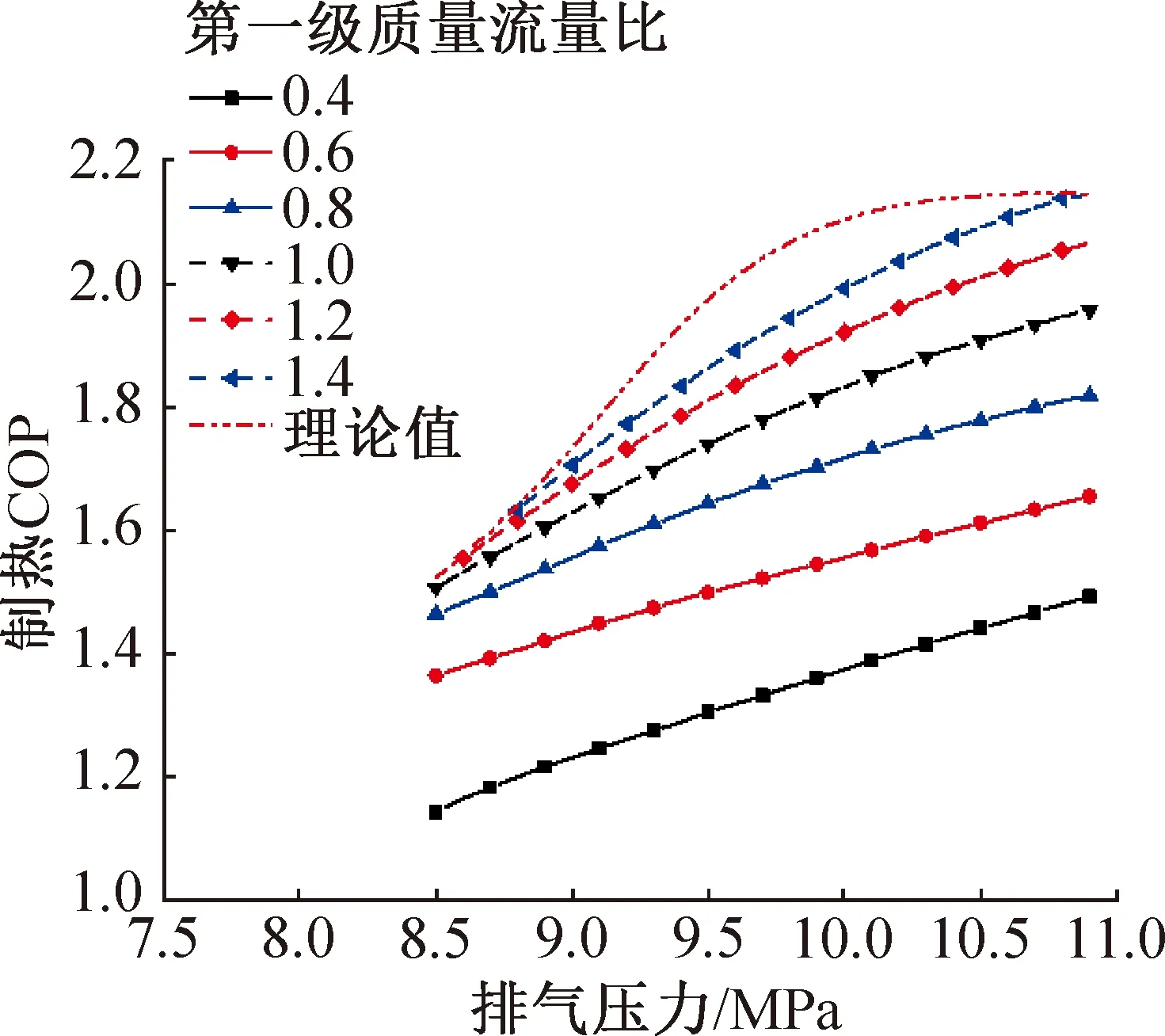
圖13 不同第一級質量流量比下制熱COP隨排氣壓力的變化Fig.13 Variation of heat coefficient of performance with discharge pressure under different first stage mass flow ratio

圖14所示為不同第一級質量流量比下，COP隨排氣壓力的變化。質量流量比越大，COP越大；此時由于最佳排氣壓力后移超過排氣壓力上限值，故所有質量流量比下均為排氣壓力10.9 MPa時的綜合COP最大，當第一級質量流量比為1.4時，最大綜合COP降至3.496，而當第一級質量流量比為0.4時，最大綜合COP僅為2.843。

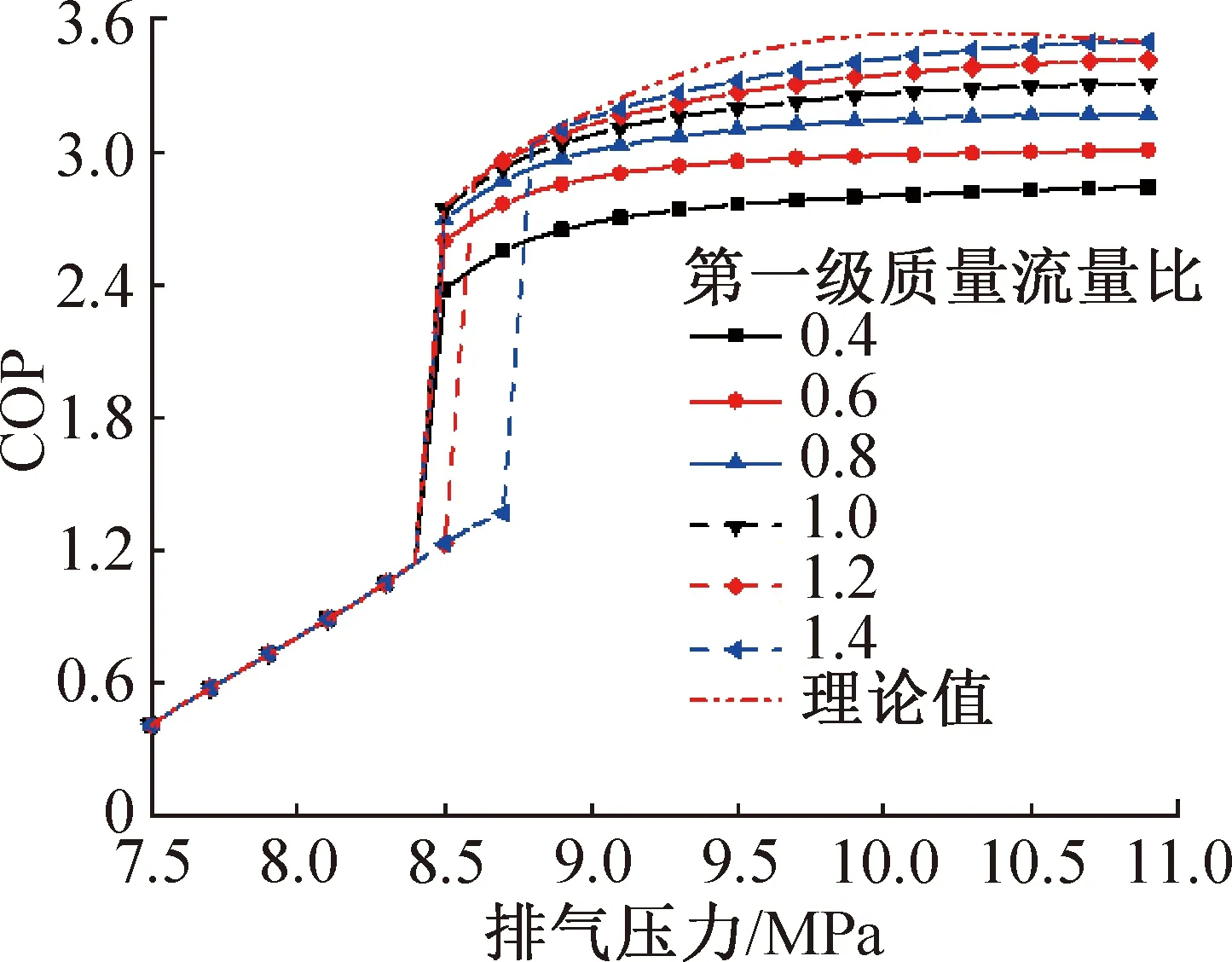
圖14 不同第一級質量流量比下綜合COP隨排氣壓力的變化Fig.14 Variation of comprehensive coefficient of performance with discharge pressure under different first stage mass flow ratio

由上述分析可知，當第一級質量流量比漸變第二級相應調節時，第一級質量流量比越大越好，同時升高排氣壓力和第二級質量流量比來降低CO2出口溫度，提升系統性能。

4 結論

本文基于人工冰場CO2制冷及熱回收系統，采用夾點分析法對雙級熱回收設計進行熱力學優化分析，得到如下結論：

1）當第二級質量流量比在0.4～1.4之間漸變，相應調節第一級質量流量比來降低CO2出口溫度時，發現應降低第二級質量流量比，升高排氣壓力，有效降低CO2出口溫度；當第二級質量流量比為0.4時，系統性能和理論保持一致，為1.4時，最大綜合COP由3.538降至3.496，同時最佳排氣壓力由10.2 MPa升至10.9 MPa。

2）當第一級質量流量比在0.4～1.2之間漸變，相應調節第二級質量流量比來降低CO2出口溫度時，應升高第一級質量流量比，同時升高排氣壓力；此時最佳排氣壓力總為10.9 MPa，且當第一級質量流量比為0.4時，最大綜合COP僅為2.843。

3）總體而言，應降低第二級質量流量比，提高第一級質量流量比，提高排氣壓力，從而提升系統綜合性能。

符號說明

m——質量流量，kg/s

h——制冷劑焓值，kJ/kg

p——制冷劑壓力，MPa

T——溫度，℃

W——壓縮機功耗，kW

Q——制熱（冷）量，kW

下標

1、2……12——相應狀態點

c——蒸發器流向壓縮機的流體

e——蒸發器流向噴射器的流體

in——壓縮機進口

out——壓縮機出口

com——壓縮機

r——制冷

hr——熱回收