園區綜合能源系統低碳經濟雙層聯合優化

譚玉華，李 臣，張 遷，陳奇林，余 諾

(1.上海理工大學機械工程學院，上海 200093;2.安徽省教育廳能源互聯網工程技術研究中心，安徽 蕪湖 241000)

0 引言

在“碳達峰”“碳中和”目標背景下，探索更高效、清潔、經濟的綜合能源利用方法及其系統規劃運行模式具有重要的理論與現實意義[1-2]。合理的規劃運行方案是保障綜合能源系統(integrated energy system，IES)發揮運營效能的必要前提。

目前，國內外學者在園區綜合能源系統規劃運行方面開展了相關研究并取得了一定成果。文獻[3]建立了含熱電聯產機組、燃氣機組和制冷裝置的園區綜合能源系統組合優化模型，以系統可靠性與經濟性為目標對系統內各設備的安裝容量進行規劃，但并未考慮系統運行期間的優化策略。文獻[4]綜合考慮規劃層面的投資成本和運行層面的運行成本，從經濟性的角度基于混合整數線性規劃方法對園區綜合能源系統的優化配置進行研究。文獻[5]在經濟性的基礎上進一步考慮可靠性指標，通過雙層協同優化方法對區域綜合能源系統的設備配置方案和日運行策略進行優化。但隨著雙碳目標的提出，只考慮經濟性、能效性和可靠性等指標為優化目標的園區綜合能源系統規劃運行已難以滿足當代社會的發展需求。除上述指標以外，還必須考慮環境污染、碳排放等環保性指標并合理衡量不同指標之間的矛盾與制約關系[6]。

為此，本文提出一種園區綜合能源系統物理模型，采用規劃-運行雙層迭代優化方法對系統的經濟性和環保性作多目標協同優化，應用非精英策略的非支配排序遺傳算法(non-dominated sorting genetic algorithm,NSGA-II)求解得到低碳經濟的最優方案，并對結果進行了對比分析。

1 園區綜合能源系統模型

綜合能源系統是指在規劃、建設和運行等階段，通過對能源的生產、運輸、分配、轉化、存儲、消費等環節進行有機協同優化后形成的多能源產供銷一體化系統[7]。其中包括直接面向終端能源用戶的園區綜合能源系統。園區綜合能源系統是一種小型系統，通常根據能量梯級利用原則對多種分布式能源設備進行綜合優化配置，從而將風能、光能、電能和天然氣等多種形式的能源轉化為冷、熱、電等負荷供用戶使用。

本文提出的園區綜合能源系統結構如圖1所示。

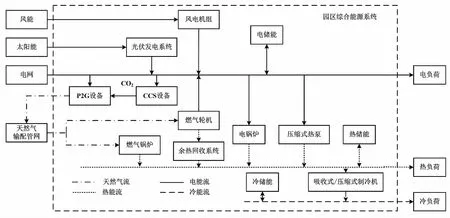
圖1 園區綜合能源系統結構示意圖

園區綜合能源系統中：電負荷需求主要由風電機組、光伏發電系統、燃氣輪機、電儲能設備和電網電力滿足；熱負荷需求主要由燃氣鍋爐、余熱回收系統、壓縮式熱泵、電鍋爐和熱儲能設備滿足；所產生的熱量通過驅動吸收式/壓縮式制冷機等空調制冷裝置進一步滿足冷負荷需求。相關研究表明[8-11],電轉氣(power to gas，P2G)技術可以將水分解為O2和H2，而碳捕集與封存(carbon capture and storage，CCS)技術可以有效捕集各設備出力過程中產生的CO2。將P2G技術和CCS技術結合之后，可以利用其中的H2和CO2合成CH4，并將CH4作為能源燃料再次使用，從而在降低碳排放量的同時減少運行燃料成本，并兼顧系統的經濟性和環保性。為了減少碳排放，系統還配置了P2G設備和CCS設備。其中：P2G設備消耗電能產生O2和H2；CCS設備捕集各設備出力過程中產生的CO2。產生的H2和捕集的CO2進一步生成CH4作為天然氣燃料循環使用。

1.1 供熱設備模型

園區綜合能源系統采用燃氣輪機和余熱回收系統作為熱電聯產(combined heat and power，CHP)機組。該機組通過消耗天然氣產生電能和熱能。其數學模型為：

(1)

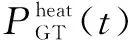
由于系統由CHP機組首先提供電負荷與熱負荷，所以當其不能滿足熱負荷需求時，由燃氣鍋爐、電鍋爐和熱泵來提供熱負荷。其數學模型為：

(2)

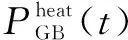
(3)

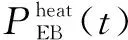
(4)

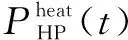
1.2 供電設備模型

園區綜合能源系統的電負荷由CHP機組、風電機組和光伏發電系統提供，并在出力不足以供應負荷需求時向電網購電。設備的數學模型為：

(5)

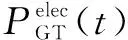
0≤PWT,k(t)≤uWT,k

(6)

式中：PWT,k(t)為第k臺風電機組在t時刻的實際出力，kW；uWT,k為第k臺風電機組的安裝容量，kW。

0≤PPV,r(t)≤uPV,r

(7)

式中:PPV,r(t)為第r臺光伏設備在t時刻的實際出力，kW；uPV,r為第r臺光伏設備的安裝容量，kW。

1.3 供冷設備模型

園區綜合能源系統的冷負荷由吸收式制冷機和壓縮式制冷機分別轉換熱能和電能獲得。設備的數學模型為:

(8)

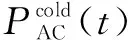
(9)

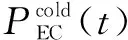
1.4 儲能設備模型

園區綜合能源內的儲能設備可以在提升系統運行經濟性的同時提高系統靈活性。本文對儲能設備的建模是基于一種廣義儲能動態的通用模型。該模型中：狀態變量為儲存的能量；控制變量為充放能功率。經過典型日運行周期內各時段的遞推，可以得到整個運行階段的狀態變化。遞推表達式為：

Qs(t+Δt)=Qs(t)+Ps,in(t)Δt-Ps,out(t)Δt,?k∈

{GCST,GHST,GBT},t∈{t1,t2,…,t24}

(10)

式中:Qs(t)為t時刻儲能設備k儲存的能量,kW·h；Ps,in(t)、Ps,out(t)分別為t時刻儲能設備k的充、放能功率,kW；Δt為單個時段的時間尺度,h；GCST、GHST和GBT分別表示蓄冷罐、儲熱罐和蓄電池。

1.5 P2G和CCS模型

P2G設備消耗電能產生O2和H2。CCS設備捕集各設備出力過程中產生的CO2，產生的H2和捕集的CO2進一步生成CH4作為天然氣燃料。P2G設備和CCS設備在運行過程中需要消耗電能，在合成天然氣的過程中需要協同運行。其數學模型為：

PP2G(t)=αDP2G(t)

(11)

式中:PP2G(t)為P2G設備產出天然氣的速率，m3/h；α為電-氣轉換系數；DP2G(t)為P2G設備消耗的電功率，kW。

DC(t)=βDP2G(t)

(12)

式中:DC(t)為P2G設備消耗對應電功率所需的CO2量，kg；β為P2G設備消耗電功率與對應CO2量的比例系數。

DCCS(t)=ωDC(t)

(13)

式中:DCCS(t)為CCS設備捕獲CO2消耗的電功率，kW；ω為CCS設備捕獲CO2的效率。

2 多目標優化模型及其求解算法

園區綜合能源系統的規劃運行聯合優化問題是一個含多目標、多約束、多變量的混合整數非線性優化問題。不同的設備配置方案、運行方式均會影響系統的實際性能。本文以經濟性和環保性為目標，對園區綜合能源系統的配置方案和運行方案進行雙層迭代優化。

綜合能源系統雙層優化模型如圖2所示。

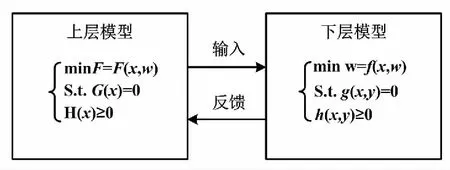
圖2 綜合能源系統雙層優化模型

上層模型研究規劃問題，以系統經濟性指標和碳排放量指標為目標函數進行設備優化配置。優化后的配置方案作為已知條件傳輸給下層模型進行運行優化。下層模型研究運行優化問題，在給定配置方案條件下對系統的運行狀態進行優化，以降低運行過程中的運行成本和碳排放量；同時，將優化結果反饋回上層進行總成本和總碳排放量的優化計算，通過循環迭代得到最優的設備配置方案和運行策略。

2.1 上層規劃模型

上層規劃模型是一個非線性多目標優化問題，優化變量是各類設備的裝配組合，安裝臺數均為整數變量。規劃目標是全生命周期總成本協同碳排放量最優。

2.1.1 目標函數

上層規劃模型的目標函數由經濟性目標Ctotal和碳排放量目標ζC兩個相互獨立的部分組成：

Ctotal=Cinv+Com+Cop+CC

(14)

式中:Cinv為系統的年化投資成本;Com為年設備維護成本;Cop為運營成本期望值;CC為所需要支付的碳交易費用。

(15)

式中:N為園區綜合能源系統內的規劃設備種類數；nv為類型為v的設備臺數；μv為類型為v的設備單價，萬元；rv為類型為v的設備折現率；yv為類型為v的設備使用壽命，年。

Com=δCinv

(16)

式中:δ為設備維護成本系數。

CC=τ(ζquota-ζactual)

(17)

式中:τ為單位碳交易價格，250元/t；ζquota為系統的碳排放配額；ζactual為系統實際碳排放量。

系統中產生單位電功率的碳排放權分配額取0.728 t/MWh,產生單位熱功率的碳排放權分配額取0.102 t/GJ。

由于經濟性目標為年總成本，所以碳排放目標也折算為年碳排放總額。

(18)

式中:ζCtotal為系統運行的年碳排放量；ζCseason為系統運行的季碳排放量。

2.1.2 約束條件

設備安裝數量受實際地域條件限制，為：

(19)

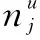
2.2 下層運行模型

下層運行模型是在上層優化配置方案確定的前提下對園區綜合能源系統典型日各個時段的運行狀態進行優化，也是非線性多目標優化問題。優化變量是各設備出力和儲能狀態，均為連續型變量。優化目標是典型日運行成本和碳排放量。一般而言，全年所有時段均需進行優化。但這會大大增加運行優化模型的變量總數和約束條件，使得模型難以求解。本文采用典型日的方法對下層運行優化模型進行構建，即根據當地的氣候環境、資源稟賦和能量供需情況，將全年劃分為幾個典型日，并統計一年中不同典型日的累積天數，再以典型日為運行周期進行運行優化模型構建。

2.2.1 目標函數

運行成本包括系統的購電和購氣費用，計算式為：

Cop=Cele+Cgas

(20)

式中：Cele、Cgas分別為系統的年購電費用和年購氣費用。

(21)

式中：cele(t)為t時刻的電價，元/kWh；cgas(t)為t時刻的氣價，元/m3；ρele(t)為t時刻的購電功率，kW；γgas(t)為t時刻的購氣功率，m3；li為第i季典型日的年化代表天數。

系統的日碳排放量表達式為：

(22)

式中：aC、bC為CHP的碳排放系數；Hν為CHP出力熱電能效比；εC為外部電網購電的碳排放當量因子；εC,g為燃氣鍋爐消耗天然氣對應的碳排放系數；εC,h為吸收式制冷機消耗熱量對應的碳排放系數；εC,e為壓縮式制冷機、電鍋爐和熱泵消耗電力對應的碳排放系數。

2.2.2 約束條件

園區綜合能源系統內多種能源通過各子系統進行匯集和分配，在運行階段需滿足以下各時刻的冷、熱、電、氣子系統能量平衡約束。

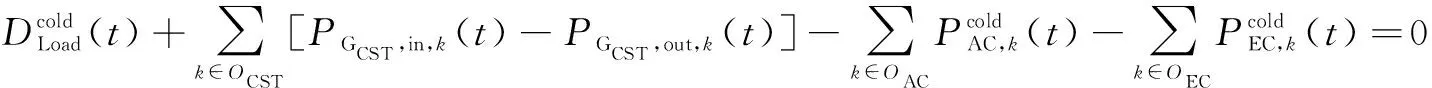
(23)

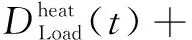
(24)

典型日t時刻熱負荷需求由系統內制熱設備產能、耗熱設備耗能及熱儲能設備配合出力進行滿足，以達到供需平衡。

(25)

典型日t時刻電負荷需求由系統內制電設備產能、耗電設備耗能及電儲能設備配合出力進行滿足，以達到供需平衡。

(26)

典型日t時刻天然氣子系統內的設備產量與購入量之和等于消耗量。

各能量轉換設備均需滿足出力上下限約束，即:

0≤Pk(t)≤uk

(27)

式中：uk為能量轉換設備k的容量上限。

2.3 模型求解算法

本文采用NSGA-II算法求解上、下層中的非線性多目標優化問題。NSGA-II算法是一種帶有精英保留策略的非支配排序遺傳算法，在多目標優化問題上具有較好的求解效果，可以通過迭代求出一組Pareto最優解集。

求解步驟如下。

①輸入NSGA-II算法參數、設備參數、典型日負荷及可再生能源出力數據。

②上層模型根據初始條件產生個數滿足約束條件的配置方案，并對其進行非支配排序，將排序結果傳遞至下層。

③下層模型依次對每種配置方案進行運行優化。每種配置方案對應生成數個設備出力方案及目標結果，并根據目標函數值進行非支配和擁擠度排序。

多目標雙層優化模型求解流程如圖3所示。

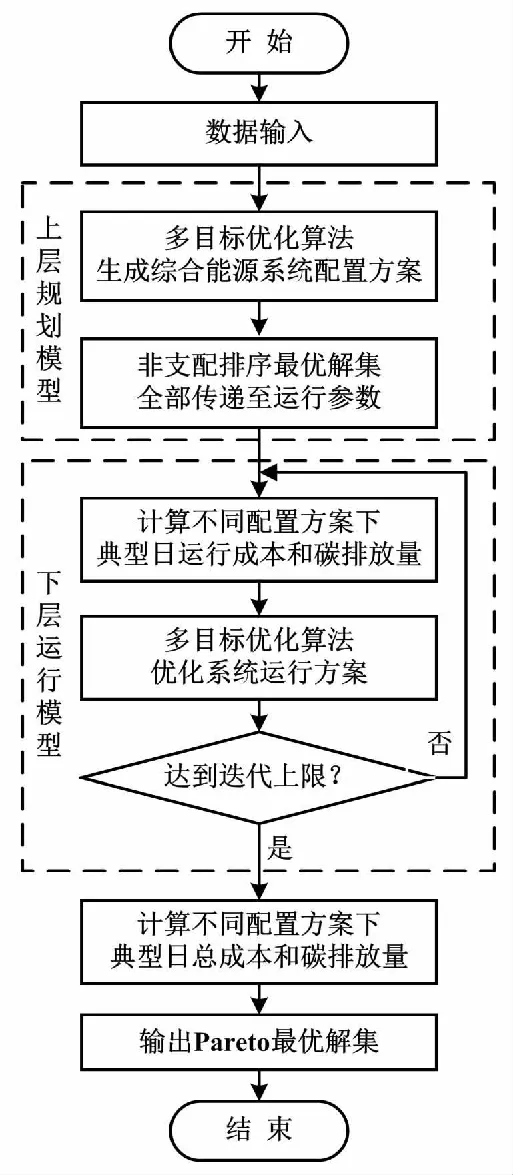
圖3 多目標雙層優化模型求解流程

④將下層模型的排序結果反饋至上層模型，計算相應配置方案的目標函數值。

⑤重復步驟③和步驟④，直至算法達到收斂條件。根據目標函數值對所有配置方案進行非支配排序，選取排名占優的非支配解集中的所有個體作為Pareto最優解集，輸出結果。

3 算例分析

本文選取蘇州某示范園區的綜合能源系統作為具體算例，基于所提模型和算法對其進行規劃-運行聯合優化。系統內碳排放計量相關的算例參數[11]如表1所示。

表1 算例參數

設備參數[12]如表2所示。

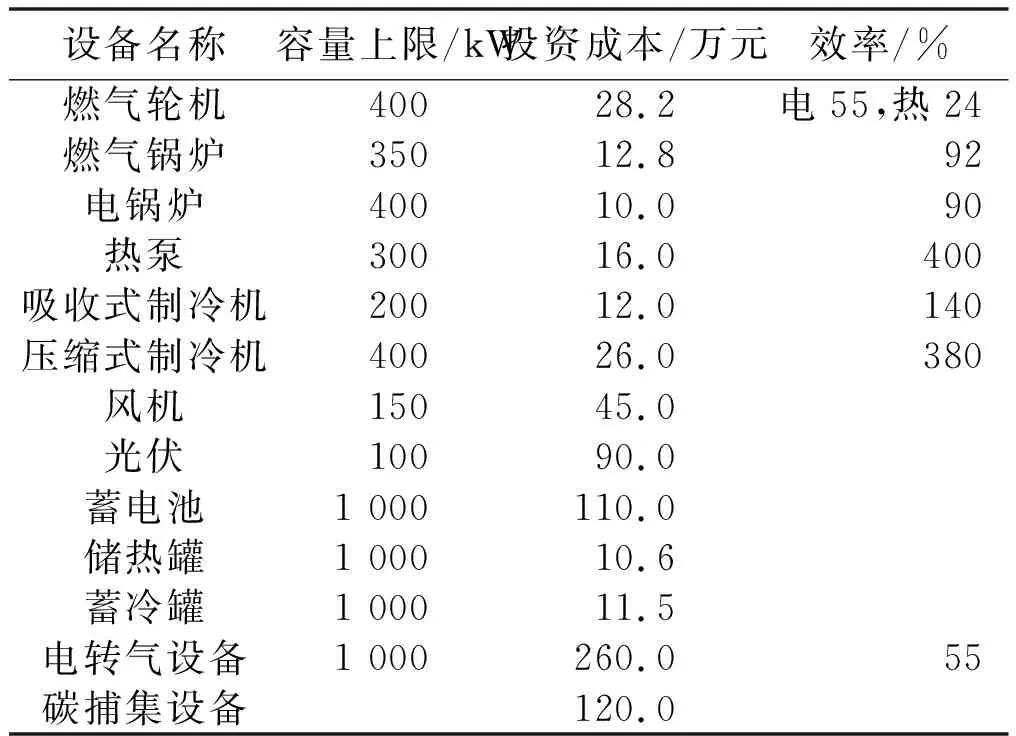
表2 設備參數

蘇州某示范園區負荷、電價、可再生能源出力曲線[5]如圖4所示。

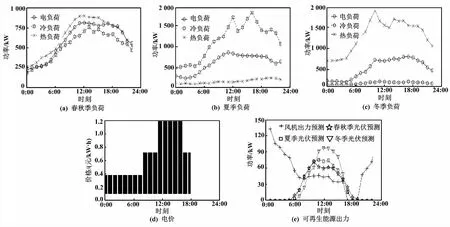
圖4 負荷、電價、可再生能源出力曲線

基于本文所提方法，對蘇州某示范園區進行規劃運行聯合優化。首先在上層模型隨機生成若干種不同的園區綜合能源系統配置方案，并按照目標函數初始期望值進行非支配排序；然后按照排序結果依次傳入運行層模型進行計算；最后將下層輸出結果反饋至上層，在反復迭代后完成多目標優化，得到一組Pareto最優解集。在解集中，各種配置方案之間無優劣之分，只在經濟性和低碳性目標之間權重不同。

Pareto最優解集分布如圖5所示。圖5直觀展示了經濟性目標和低碳性目標間的關聯性，從中選取典型方案進行分析。由于不同季節典型日內系統的冷、熱、電負荷需求不同，所以在規劃階段需要考慮各類負荷的上限來配置設備。而在運行階段，則需要針對不同季節典型日冷、熱、電負荷的需求差異優化設備出力。

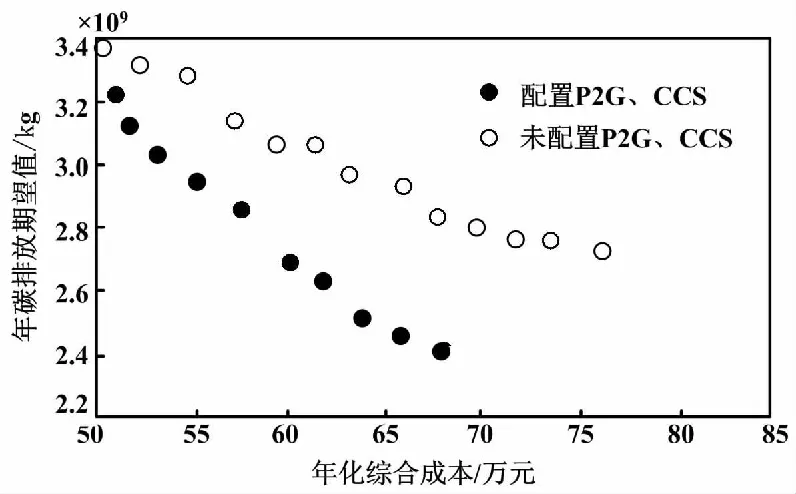
圖5 Pareto最優解集分布圖

此處選取方案1作為典型方案對設備出力優化結果進行分析。

IES典型配置方案如表3所示。

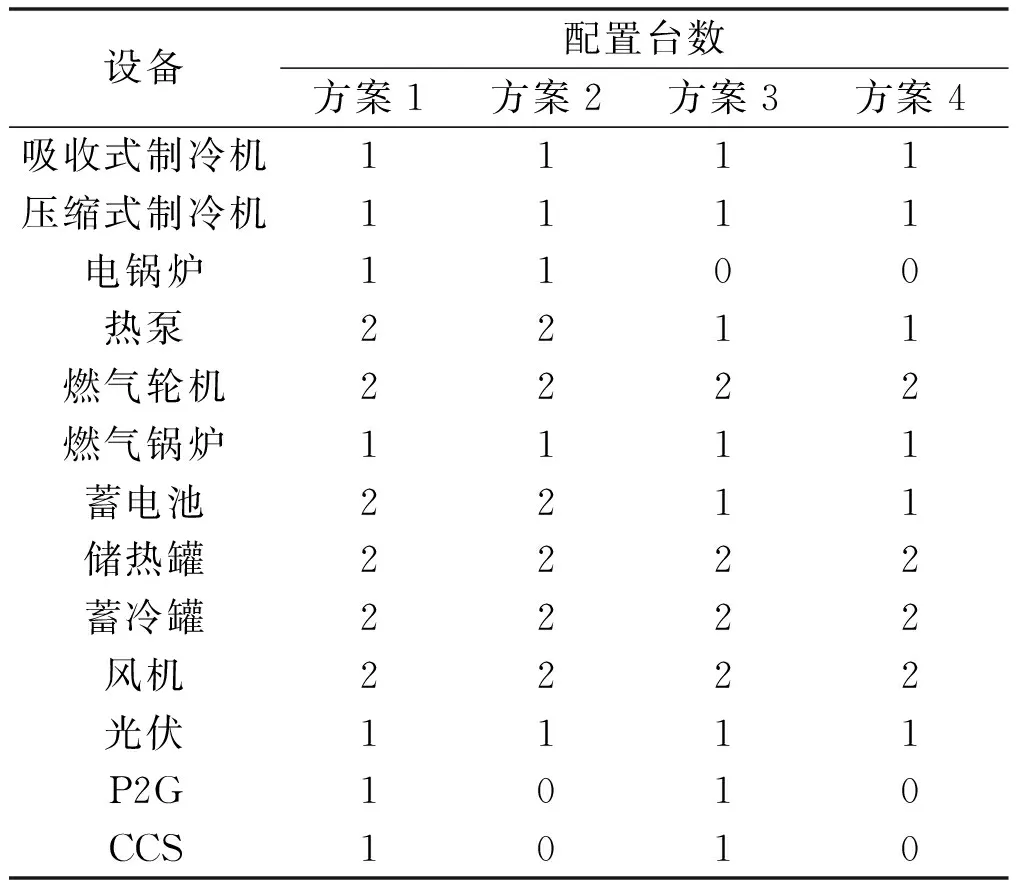
表3 IES典型配置方案

典型日最優運行方案如圖6所示。

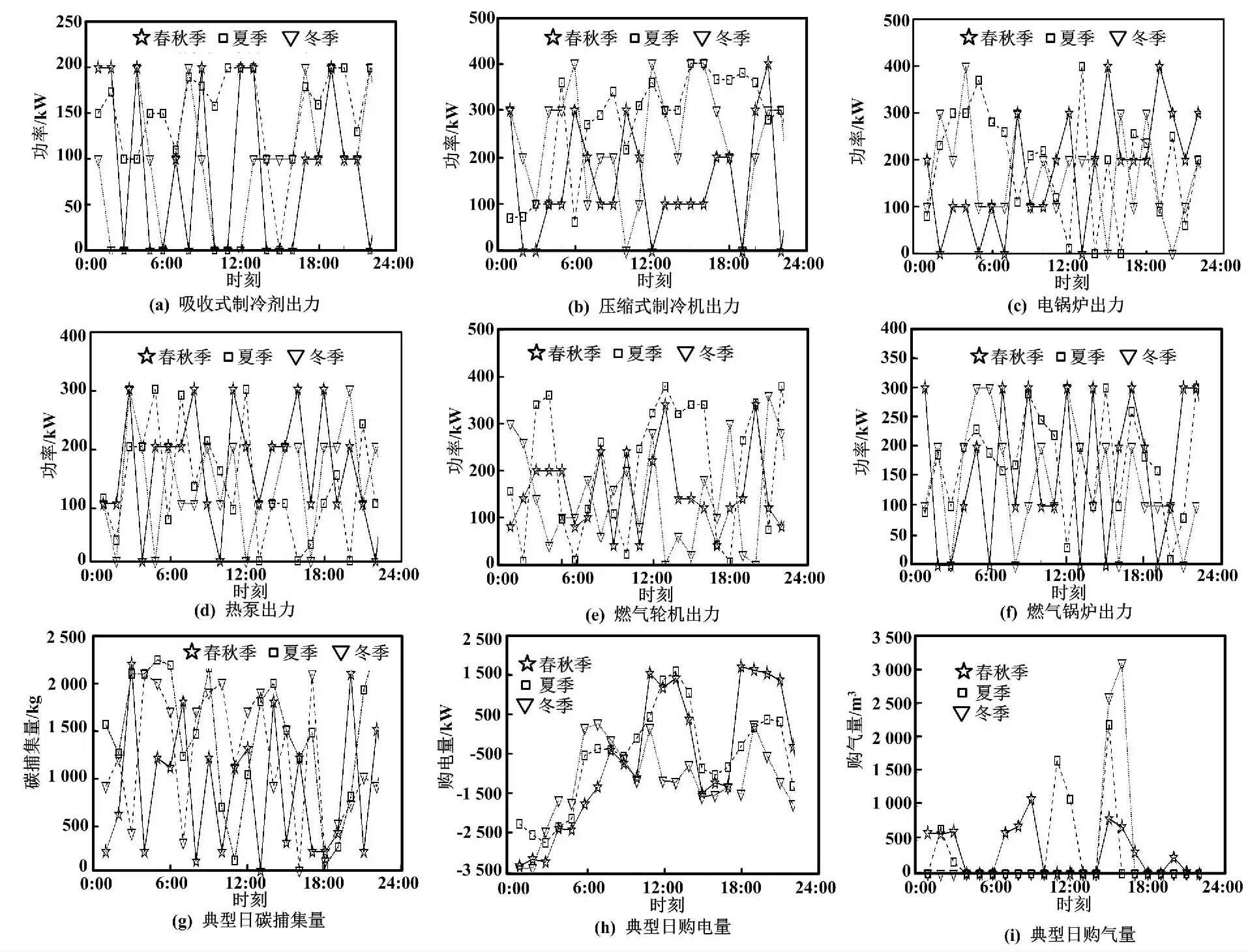
圖6 典型日最優運行方案

圖6(a)～圖6(f)為不同季節典型日內各能量轉換設備在各時刻的出力情況。圖6(g)為碳捕集設備在不同季節典型日內各時刻碳捕集量。圖6(h)和圖6(i)分別為不同季節典型日內各時刻系統的購電量和天然氣購入量。由圖6可知，在夏季典型日內供熱設備出力較少，而供冷設備出力較多；在冬季典型日內則是供熱設備出力較多，供冷設備減少出力；在春秋季典型日內各設備出力曲線較為集中，各設備出力較為均衡，與其冷、熱負荷需求差異較小有關。不同典型日內購電量曲線走勢基本一致，在用電高峰時段從電網購入，在低谷階段售出多余電能。而由于配置了P2G設備，天然氣購入量持續較少，在碳捕集量較低的時段，天然氣購入量有所升高，對應了P2G和CCS設備的出力耦合情況。

根據上層模型確定的配置方案及下層模型優化的運行階段設備出力情況，可計算典型方案的年平均成本和年碳排放量。

性能指標結果如表4所示。

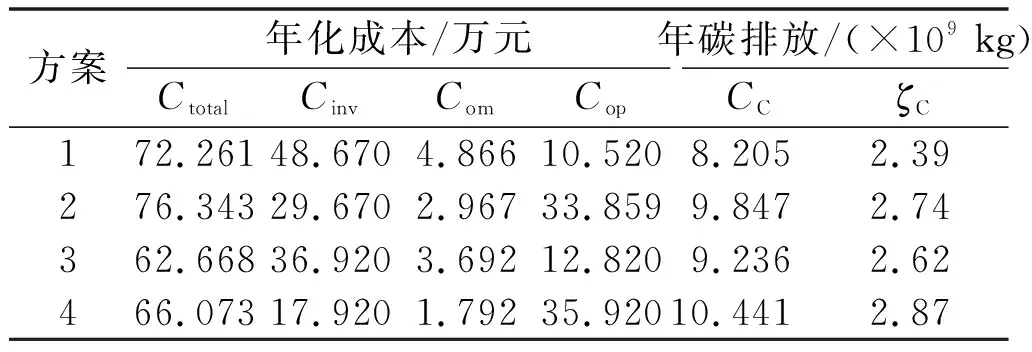
表4 性能指標結果

由表4可知，方案1、方案3與方案2、方案4相比，前二者的碳排放量明顯降低。其中，方案1比方案2多降低12.8%的碳排放量、方案3比方案4多降低8.7%的碳排放量。這表明，配置了P2G和CCS設備的系統，在降低碳排放方面效果顯著。在經濟性方面，配置了P2G和CCS設備的系統投資成本增加，但運行成本和碳交易成本都有所下降，總成本節省約5%。這表明，在設備壽命周期內，配置P2G及CCS設備不僅可大幅減少系統碳排放量，還可實現總成本的降低，兼顧了經濟性與低碳性。

4 結論

在雙碳目標背景下，針對現有研究中的不足，本文考慮在園區內引入P2G和CCS設備，提出了一種園區綜合能源系統物理模型。在對系統內設備及能量轉換關系進行數學建模的基礎上，充分考慮系統不同配置方案、運行策略、季節變化和日內時序變化影響。算例結合規劃-運行兩個層面，對于系統的經濟性和碳排放量，采用雙層迭代優化方法對其進行綜合衡量和多目標協同優化，并采用NSGA-II算法求出系統優化配置方案和運行方案的Pareto最優解集。該解集可以進行直觀展示和量化分析，為規劃運行人員提供理論依據，幫助他們根據具體需求進行側重選擇并作出切合實際的最優決策。仿真算例及不同方案對比分析結果表明，所提系統模型在規劃年限平均總成本相近時可有效降低系統碳排放量，同時也驗證了所提雙層規劃運行模型及其算法的有效性。