基于格子Boltzmann方法的靜壓轉臺流場動態分析

常 斌， 段鸞芳

(1.江蘇聯合職業技術學院泰興分院機電工程系， 江蘇泰州 214599；2.南京工業職業技術大學電氣工程學院， 江蘇南京 210023)

引言

《中國制造2025》中明確提出高檔數控機床和機器人是十大重點發展領域之一，高檔數控機床的高速、高精、高效發展有助于推動我國制造業的創新升級[1-2]。轉臺作為高檔數控機床中的關鍵部件，對數控機床的可靠運行起著至關重要的作用。靜壓轉臺由于油膜具有吸振作用且摩擦系數小，已廣泛應用于重載場合。前人針對靜壓轉臺提出了諸多腔體結構，并對油液的流動進行了深入探討[3-4]。

在結構方面，王永柱等[5]利用Fluent對矩形油墊中的油腔結構進行了分析， 結果表明口字形比工字形結構具有更好的承載能力。劉云鵬等[6]設計了一種新型靜壓轉臺，解決了重載下油膜厚度較小，流入流量小于泄漏量的問題。王京等[7]設計了一種雙環形油腔，并探究了入口雷諾數對油液在油腔內部及油腔承載能力的影響。張慶鋒[8]利用CFD對數控磨床扇形靜壓轉臺的油膜特性進行了分析。在承載力方面，安汝偉等[9]對定量閉式靜壓轉臺的支承力進行了等效計算。劉志峰等[10]利用有限差分法研究了油墊溫度與重載靜壓轉臺承載力之間的關系。陳令等[11]利用ANSYS研究了大型立式磨床靜壓工作臺在不同轉速下的油膜溫升結果。劉志峰等[12]針對定量扇形靜壓轉臺探討了整體動力學模型，并通過實驗進行了驗證。申峰等[13]利用PIV和CFD分析了數控機床靜壓系統中的流場特性。劉趙淼等[14]探討了入口油液雷諾數對靜壓油腔承載能力的影響，雷諾數的變化將改變流線中渦的位置。

本研究將針對油液在環形靜壓轉臺內部的流動展開研究，利用LBM重點研究封油邊間隙高度、入口速度及油液黏度3個因素對油液流動、速度分布及承載能力的影響。

1 LBM方法

LBM具有物理過程清晰，計算方便，易編程實現等優點，已廣泛應用于工業制造領域[15-17]。其將流體流動看成是微觀粒子在不同方向的運動，根據運動情況主要包含遷移和碰撞兩種情形[18]，LBM的一般性方程如式(1)所示：

fi(r+eiδt,t+δt)-fi(r,t)=

(1)

式中,fi—— 某時刻的瞬時運動方程

r—— 位移

t—— 時間

ei—— 速度配置

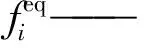
在二維流動中常用D2Q9(二維九向)模型，其速度配置具體為：

(2)

式中,e—— 基本速度

e取決于格子步長δx和時間步長δt，具體為e=δx/δt。式(1)中τ為松弛時間，其與動力黏度μ相關，如式(3)所示：

(3)

式中，ρ—— 密度

(4)

式中，ωi—— 權重系數

cs—— 格子聲速

u—— 速度

ωi與粒子運動方向相關，其具體數值為：

(5)

(6)

密度ρ與速度u的表達式如式(7)所示：

(7)

在對實際問題仿真分析時，具體流程如下：

(1) 量綱轉換，LBM為無量綱方法，在實際分析時，需要進行實際物理量與計算物理量的轉換，此處以雷諾數作為準則數；

(2) 確定計算域及初始條件(如初始速度、初始密度、初始壓力、雷諾數、松弛時間、流體黏度等)；

(3) 根據式(4)確定平衡態分布方程；

(4) 根據式(1)進行分析計算，包含遷移和碰撞2個步驟；

(5) 進行邊界處理，這里采用常用的非平衡外推格式[19-20]；

(6) 根據式(7)計算密度和速度；

(7) 設定一較小誤差值，計算上一循環步與當前循環步之間的差值，當此差值小于設定的誤差值時，則滿足精度要求，跳出循環，否則轉至步驟(3)繼續執行下一次循環計算；

(8) 根據步驟(1)中的量綱轉換，反向計算宏觀物理量值。

2 油腔外形參數及仿真方案

靜壓轉臺雙環形的油腔如圖1所示，其具體參數如表1所示。

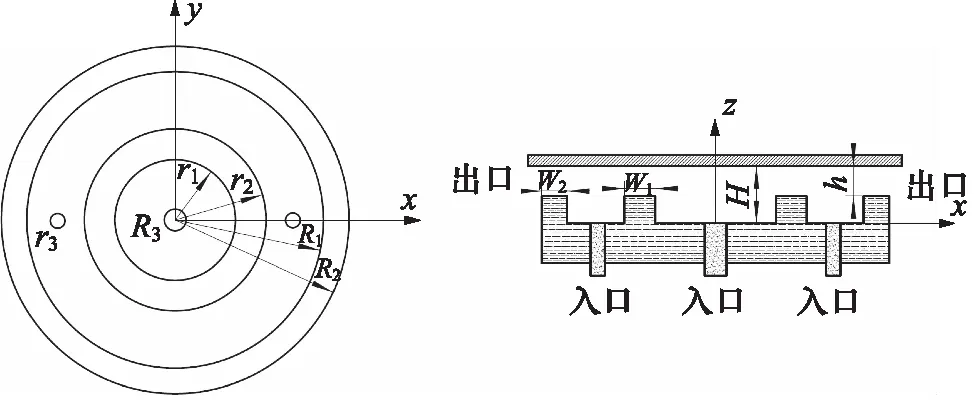
圖1 雙環形油腔

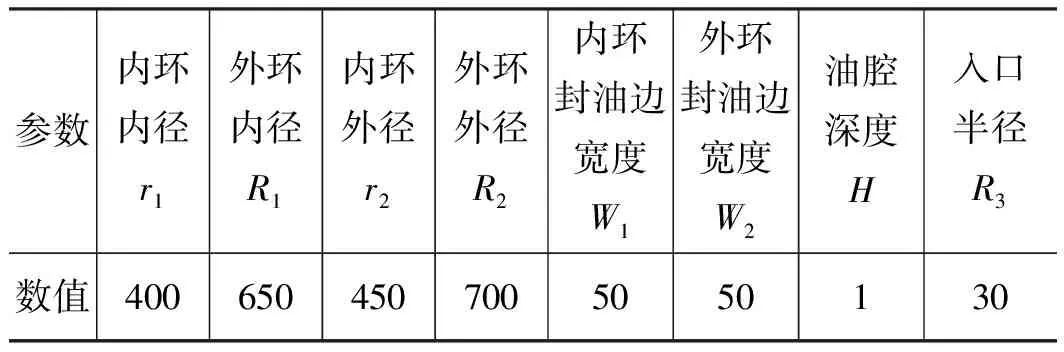
表1 雙環形油腔的幾何參數Tab.1 Geometry parameters of double rings oil chamber mm

為了充分考慮不同因素對油液在油腔內流動的影響，選取封油邊間隙高度、油液入口速度以及油液黏度3個因素進行深入分析，共列出如表2所示的7種組合方案，其中油腔深度H設定為11 mm。由于油腔結構具有對稱性，為了節省計算資源，取其中一半結構進行分析。利用MATLAB結合LBM方法，對表2中的7種方案進行了仿真分析，獲得的流線圖如圖2所示，顏色越深表示渦的程度越強烈。

表2 流動仿真方案Tab.2 Simulation cases of flow

3 油液流動分析

3.1 封油邊間隙高度的影響

根據圖2a～圖2c所示，主渦的數量一共有6個，當封油邊間隙高度較小時，主渦的強度不一，第一主渦附近有諸多小渦形成，隨著封油邊間隙高度的逐漸增加，小渦有逐漸融入主渦的趨勢，且第一入口引起的渦流會逐漸影響到外側凹槽區域。封油邊處水平速度沿徑向的變化曲線如圖3所示，主要的區別在內部，其中案例2對應的速度分布差距較大，案例1速度變化相對較小，而在右端出口處速度幾乎一致。轉臺的承載力曲線如圖4所示，隨著間隙高度的增加，中心凹槽與外側凹槽內承載力的差值越來越小，在案例3中，中心凹槽與外側凹槽內的承載力近乎無差別，說明當間隙過大時，環形設置將不再影響轉臺的承載能力。

3.2 入口速度的影響

根據圖2a、圖2d、圖2e所示，流線圖表明入口速度主要影響了第一主渦、第四主渦以及小渦的形成與強烈程度。出口封油邊處水平速度沿徑向的變化曲線如圖5所示，入口速度越大，水平速度沿徑向分布的差距越小，當入口速度為0.10 m/s時，速度差距較大，最大差值達到了0.025 m/s，但在封油邊出口處的速度幾乎均為0 m/s。轉臺的承載力曲線如圖6所示，由圖可知，速度越大，承載力越大，而環形設置引起的中心凹槽與外側凹槽承載能力的差值近乎相等。

3.3 油液黏度的影響

根據圖2a、圖2f、圖2g所示，黏度越大，流線的分布情形越簡單，對第一主渦及第四主渦的影響最為明顯。出口封油邊處水平速度沿徑向的變化曲線圖如圖7所示，黏度對速度分布影響較為明顯，但無明顯規律，速度波動最明顯出現在案例7中，速度波動最小的出現在案例6中，出口速度均為0 m/s，則無油液漏出。轉臺的承載力曲線如圖8所示，黏度較小的案例中呈現出較好的承載能力，隨著黏度的增加，中心凹槽與外側凹槽承載力的差值逐漸增大。

4 結論

(1) 油液封油邊間隙高度影響了主渦的形成，尤其體現在第一主渦，隨著間隙高度的增加，中心凹槽的區域會逐漸影響到外側凹槽區域，封油邊沿徑向的速度受出口間隙高度的影響較明顯，且未呈現出特定規律，當間隙較小時，通過環形設置，外側凹槽的承載能力有明顯提升;

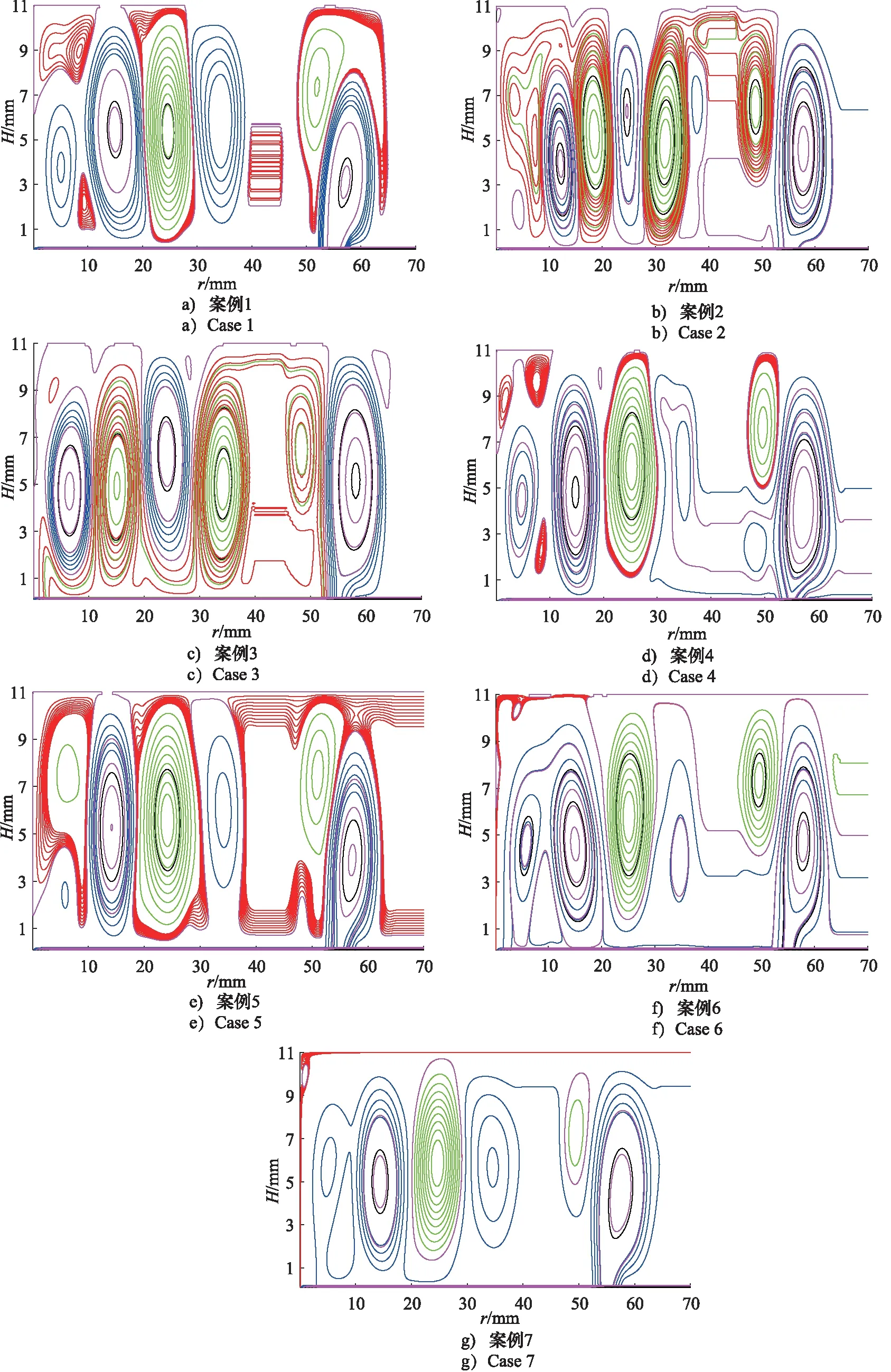
圖2 不同案例油腔內部的流線圖Fig.2 Streamlines of oil in chamber for different cases

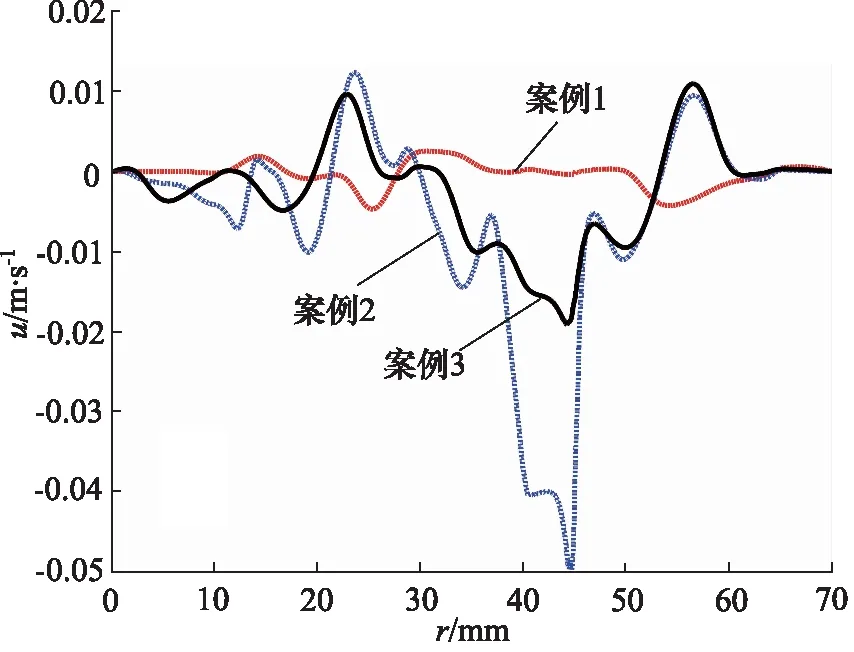
圖3 案例1～3的封油邊徑向速度分布Fig.3 Radial velocity distribution at sealing edge for case 1～3

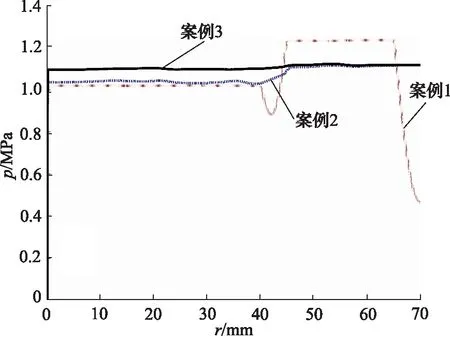
圖4 案例1～3的壓力分布曲線Fig.4 Pressure distribution curves for case 1～3

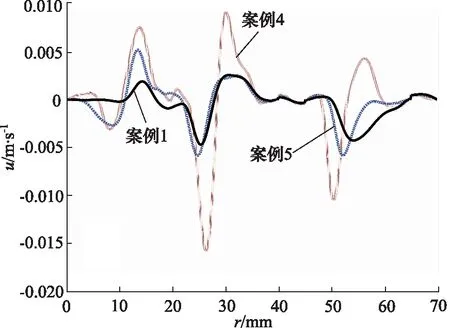
圖5 案例4，5，1的封油邊徑向速度分布Fig.5 Radial velocity distribution at sealing edge for case 4,5,1

(2) 油液入口速度對流線、封油邊徑向速度分布以及承載能力有明顯影響，入口速度越小，封油邊徑向速度波動越明顯，但承載能力越差；

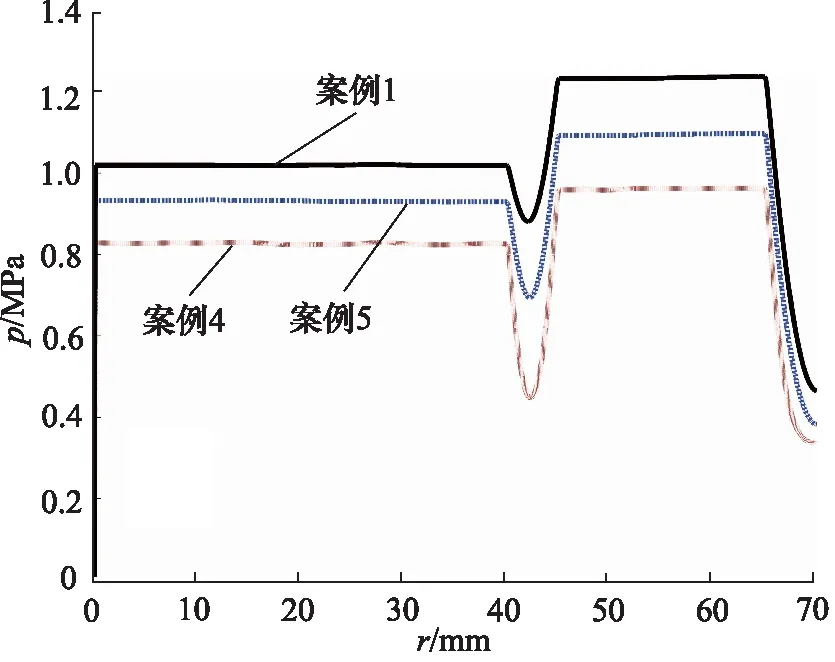
圖6 案例4，5，1的壓力分布曲線Fig.6 Pressure distribution curves for case 4,5,1

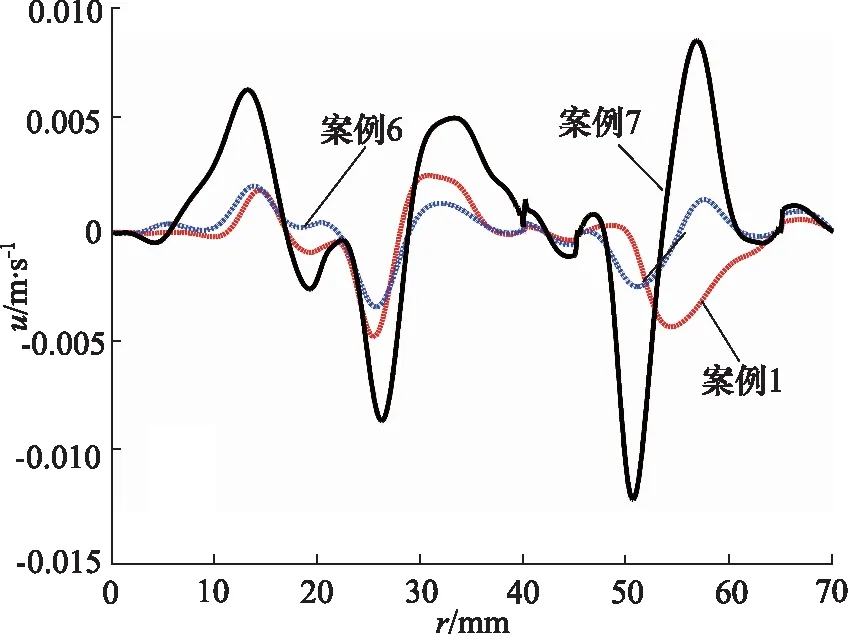
圖7 案例1，6，7的封油邊徑向速度分布Fig.7 Radial velocity distribution at sealing edge for case 1,6,7

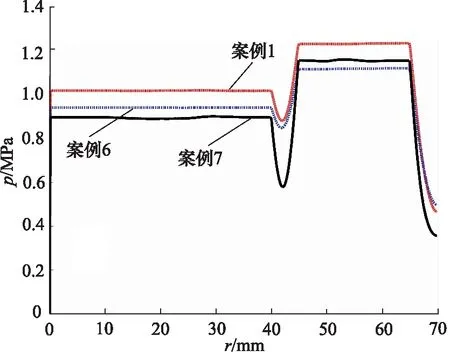
圖8 案例1，6，7的壓力分布曲線Fig.8 Pressure distribution curves for case 1,6,7

(3) 油液黏度對主渦有重要影響，尤其體現在第一主渦和第四主渦上，油液黏度越小，承載能力越好，外側凹槽與中心凹槽承載力的差值隨黏度的增加而增大。