基于奇異值分解的雙算法織物缺陷檢測

鄭兆倫， 魯玉軍

(1.浙江理工大學 機械工程學院， 浙江 杭州 310018； 2.浙江理工大學龍港研究院， 浙江 溫州 325802)

在紡織品生產過程中，織物表面缺陷嚴重影響了產品質量，因此織物缺陷檢測是紡織行業中必不可少的一個重要環節。目前，大部分工廠仍在采用傳統的人工檢測方法[1]，此方法雖然可以做到即時糾正一些錯誤，但是疲勞會導致不可避免的人為錯誤，并且通常難以檢測到較為微小的織物瑕疵，成功率僅為60%～75%[2]。隨著工業4.0的推廣，視覺實時檢測技術逐漸在織物疵點識別中應用。

目前，針對織物疵點檢測主要分為以下4種方法：基于結構的方法、基于統計的方法、基于頻譜的方法以及基于學習的方法[3]。基于結構的方法中，周文明等[4]提出視覺顯著性算法，通過選取若干個與其最相似的圖像塊，計算與該圖像塊的差異值之和，并生成顯著性圖，最后對顯著性圖像進行閾值分割得到疵點。Dhivya等[5]在文中使用多尺度輪廓的方法提取邊緣圖，基于提取輪廓的特征由K最鄰近方法(KNN)分類器提取和分類，所得結果較支持向量機(SVM)、受限制的玻爾茲曼機(RBM)和極限學習機(ELM)有更好的性能結果。基于統計的方法中，孫國棟等[6]提出一種基于灰度共生矩陣的反向投影算法，結合灰度共生矩陣紋理特征提取的特點和反向投影算法突出小物體的特性來獲得疵點。Jing等[7]根據形態成分不同分離織物背景和前景，再重新組合獲得去噪后的織物圖像，以確保更精確織物瑕疵定位。何峰等[8]提出窗口跳步形態學算法，通過直方圖均值化及設計形態學核做腐蝕運算，快速定位出疵點位置。Jiang等[9]提出了一種區域Sobel算法，通過Sobel算子進行區域劃分，再對每個區域采用閾值分割確定疵點。基于頻譜的方法中，顧菁等[10]提出基于小波變換與局部熵的織物疵點檢測方法，先進行小波變換，然后分別計算正常織物和缺陷織物局部熵值，對比二者差值大小，設定差閾值識別并確定疵點。Li等[11]采用最優橢圓Gabor濾波器(EGF)代替Gabor濾波器，并采用隨機漂移粒子群算法確定最優橢圓Gabor濾波器的最優參數，通過卷積的方式分離織物的背景和瑕疵。基于學習的方法中，Qin等[12]在現有的殘差模塊的基礎上，增加一個新的卷積分支，根據網絡層數動態調整感受野的大小，從而提出一種新的主干網絡Hourglass-MRB，較原模型相比織物瑕疵識別率有較大的提升。Li[13]等利用多個帶有多層感知器的微體系結構對網絡進行優化，微體系結構的主要組成部分采用多尺度分析、濾波器因子分解、多位置池化和參數約簡等技術構建，以提高緊湊模型中的檢測精度，證實所提出的網絡模型尺寸更小且檢測精度更高。

以上針對紋理織物缺陷檢測的算法，對缺陷與背景對比度較高，以及織物圖量較大時有較好的檢測效果，但對缺陷與背景對比度較低且織物圖量有限時檢測效果并不理想。針對上述問題，本文選用不同對比度的缺陷織物作為研究對象，利用織物背景和不同缺陷的差異性，采用基于奇異值分解的雙算法織物缺陷檢測技術，以期在織物缺陷與背景對比度較低時生成較優的檢測效果圖。

1 織物缺陷分類和算法檢測流程

1.1 織物缺陷分類

本文根據織物缺陷特點從總體上把織物缺陷分為2類：洞形缺陷和線形缺陷，并通過織物缺陷處圖像灰度方差值的大小來判定其屬于何種缺陷。如圖1(a)所示，該缺經織物圖處的缺陷較窄，通過計算可得缺陷處的方差值較大，該缺陷被判為線形缺陷。當缺經織物圖處的缺陷足夠寬時，如圖1(b)所示，其缺陷處的方差值則較小，此時可以判定該缺陷為洞形缺陷。

圖1 缺經織物缺陷圖片Fig.1 Picture of fabric with warp defect. (a) Linear defect; (b) Hole shape defect

綜上所述，通過定量的方式來劃分織物缺陷類型，可以很好的解決現有疵點的形態與尺寸變化范圍較大而難以劃分類別的難題。

1.2 基于奇異值分解的雙算法流程

本文所用測試圖像來自天池布匹缺陷數據庫，圖像像素大小為2 560×1 920。本文采用像素大小為256×256的窗口對采集到的圖像進行分割，利用多線程操作提高圖片處理速率，效果較好。示例圖像如圖2所示。

圖2 示例圖像Fig.2 Sample images. (a) Linear defect; (b) Hole shape defect

分割后的圖像作為輸入圖像，其處理流程如圖3所示。

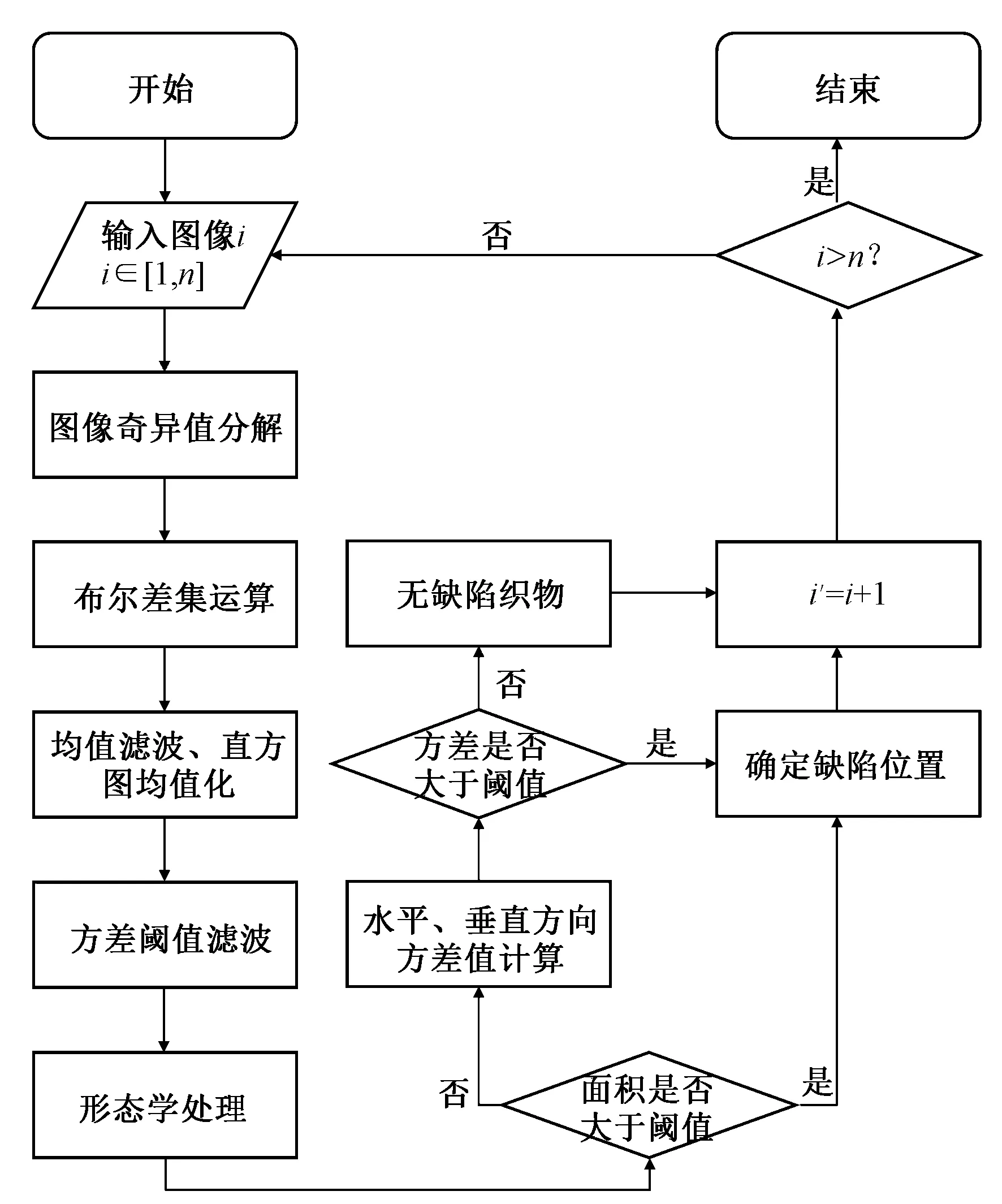
圖3 算法流程圖Fig.3 Algorithm flow chart

第1步，對輸入的灰度圖像進行奇異值分解，計算出輸入圖像特征值和特征向量，選取若干項組成特征值圖像；

第2步，用原圖像與特征值圖像做布爾差集運算模糊圖像背景區域獲得差值圖；

第3步，采用均值濾波以及直方圖均值化增強缺陷區域和背景區域之間的對比度；

第4步，通過設定方差閾值的方式初步確定織物缺陷的位置；

第5步，采用形態學開運算和膨脹運算消除噪聲點干擾并擴大缺陷區域；

第6步，通過判斷形態學處理之后缺陷面積區域是否大于閾值，是則證明此為洞形缺陷，確定其位置并令圖像編號i′=i+1，否則進行水平和垂直方差計算并判斷方差是否大于閾值，是則證明此為線形缺陷，確定缺陷位置并令圖像編號i′=i+1，否則證明此為正常織物并令圖像編號i′=i+1；

第7步，判斷圖像編號是否滿足i>n，是則說明所有缺陷已經檢測完畢，結束檢測，否則選取圖像編號i進行檢測。

2 基于奇異值分解的雙算法檢測

2.1 奇異值分解及布爾差集運算

數字圖像數據可以用矩陣來表示，因此可以采用矩陣理論和矩陣算法對數字圖像進行分析和處理。在織物圖片中存在大量相似紋理，由于需要檢測的是面積較小的織物缺陷，因此這些紋理在圖像處理中被視為冗余信息，在檢測時應盡可能過濾以減小對檢測結果的影響。奇異值分解可以針對任意形態的矩陣作特征值分解，本文采用此方法過濾冗余信息，奇異值分解如式(1)所示。

(1)

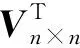
(2)

圖4(a)為輸入缺陷原圖，分別為洞形缺陷和線形缺陷，對輸入圖像進行奇異值分解后，取前4項特征值和特征向量組成特征值圖，效果如圖4(b)所示，可以看出洞形缺陷的織物背景和織物缺陷能較好的分離，而線形缺陷分離效果較差，這是由于線形缺陷圖片中織物缺陷面積較大，對特征值和特征向量產生了較大的影響，致使不能很好的分離缺陷和背景。通過把分離獲得的特征值圖和織物原圖做布爾差集運算得到差值圖，其效果如圖4(c)所示。

注：1—洞形缺陷織物；2—線形缺陷織物。圖4 原圖與特征值圖布爾差集運算Fig.4 Boolean difference set operation between original graph and eigenvalue graph. (a) Defects in original image; (b) Defect eigenvalue diagram; (c) Defect difference chart

2.2 均值濾波及直方圖均值化

均值濾波是典型的線性濾波算法，其原理如式(3)所示。式中，g(x,y)是原像素；I(x,y)是相鄰像素，即用模板中像素的平均值來代替原來像素值。差值圖進行均值濾波的目的是消除缺陷位置的噪聲點，使缺陷更加平滑，如圖5(a)所示。

注：1—洞形缺陷織物；2—線形缺陷織物。圖5 均值濾波及直方圖均值化Fig.5 Mean filtering and histogram averaging. (a) Defect mean filtering; (b) Histogram averaging

(3)

直方圖均衡化又稱直方圖平坦化，實質上是對圖像進行非線性拉伸，重新分配圖像像元值，使一定灰度范圍內像元值的數量大致相等，讓原來直方圖中間的峰頂部分對比度得到增強，而兩側的谷底部分對比度降低，使輸出圖像的直方圖變成一個較平的分段直方圖，產生粗略分類的視覺效果。對均值濾波之后的圖像進行直方圖均值化使得織物背景區域的灰度方差值增大，而缺陷區域灰度方差值不變，效果如圖5(b)所示。

由圖5(b)可知，經過均值濾波和直方圖均值化后，洞形缺陷織物中缺陷部分的灰度值方差與背景部分灰度值方差相比有較大的差距，而對于線形缺陷，其差值圖效果較差，所以在均值濾波和直方圖均值化后缺陷和背景沒有被很好的劃分，難以從處理后的圖片中采用灰度值方差的方式確定缺陷位置。

2.3 方差閾值濾波

把經過均值濾波和直方圖均值化的圖像進行方差閾值濾波，可以初步確定缺陷位置，濾波原理如式(4)、(5)所示。

(4)

(5)

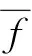
(6)

式中，lij為執行方差濾波的濾波核，其根據洞形缺陷的特點，設計為的十字形，如圖6所示，此核的設計方式不僅能有效去除噪聲點的干擾并且能較大限度地保留缺陷區域。

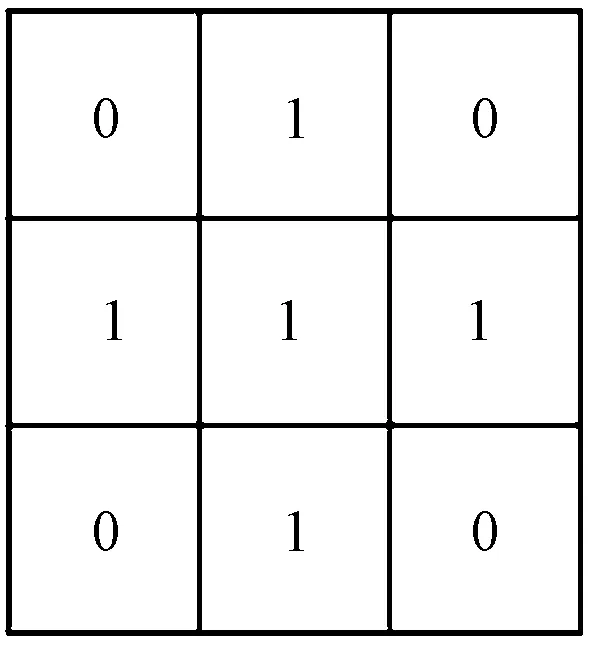
圖6 方差閾值濾波核Fig.6 Variance threshold filter kernel

為提高方差濾波的魯棒性，本文采用全圖比例方差值來確定方差閾值，即在計算出整張圖片像素方差值S2后，將該值乘以方差比例系數k，所得結果作為方差閾值。由于本文研究對象為具有紋理的織物，其背景區域方差值遠大于缺陷區域方差值，即缺陷區域具有小方差值的特點，因此本文選用k=5%作為方差閾值濾波的比例系數。通過動態方差閾值濾波的方式，能夠使缺陷的提取具有較好的適應性。

在設定參數后，首先將構造的濾波核遍歷均值化圖像后得到方差值圖，再通過設置方差閾值的方式，去除灰度方差值較大的背景區域，最終保留下灰度方差值較小的缺陷區域，其效果如圖7所示。

圖7 方差閾值濾波Fig.7 Variance threshold filtering.(a) Linear defect;(b) Hole shape defects

2.4 形態學處理

形態學處理是利用數學形態學對分割后的織物圖像進行背景修正，用于從圖像中提取對表達和描繪區域形狀有意義的圖像分量，使后續的識別工作能夠抓住目標對象最為本質的形狀特征。基本運算有腐蝕、膨脹、開運算和閉運算，膨脹和腐蝕運算原理如圖8所示。

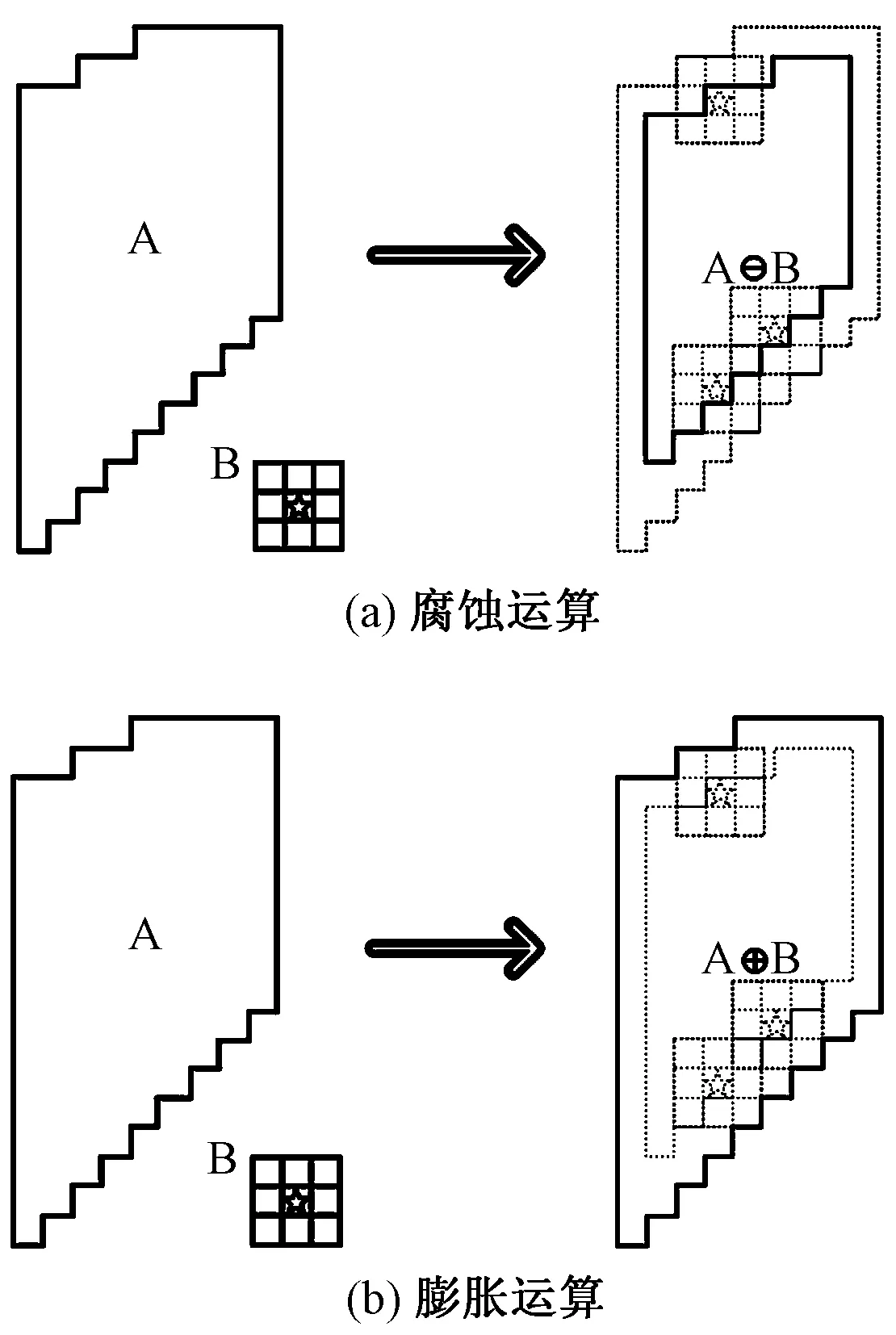
圖8 膨脹和腐蝕運算原理圖Fig.8 Schematic of expansion and corrosion operations. (a) Erosion operation; (b) Dilation operation

圖中A為需要處理的圖像，B為處理圖像的核。膨脹為求局部最大值的操作，即核B與圖形卷積，計算核B覆蓋的區域的像素點的最大值，并把這個最大值賦值給參考點指定的像素，其作用是填充分割后疵點圖像的邊緣凹陷、內部溝槽等。腐蝕則是求局部最小值的操作，用于消融疵點圖像的邊界點，將小于結構元素的雜散疵點圖像去掉，例如毛刺、孤立點凸角等。

開運算是先腐蝕后膨脹，其作用是去掉某些疵點圖像邊緣毛刺和孤立點、銳化角的同時也使其邊緣平滑。閉運算是先膨脹后腐蝕，其作用填平疵點圖像內部細小溝槽的同時也去掉了某些邊緣雜散點[15]。

由圖7可知洞形缺陷方差閾值濾波之后缺陷位置比較明顯，但還存在噪聲點的干擾，為此先采用形態學開運算去除較小的噪聲點，再使用膨脹運算擴大缺陷面積，其效果如圖9所示。

注：1—洞形缺陷織物；2—線形缺陷織物。圖9 形態學處理Fig.9 Morphological processing. (a) Defect opening operation; (b) Defect expansion operation

2.5 面積閾值判別

由圖9(b)可知經過形態學處理之后的圖片噪聲點干擾已經大幅度降低，洞形缺陷中存在著織物缺陷區域和少量噪聲點，而對于線形缺陷而言，形態學處理之后僅含有少量的噪聲點。根據此特征來判斷洞形缺陷和線形缺陷類別，其步驟為：1)計算洞形缺陷和線形缺陷的最大連通域面積；2)判斷最大連通域面積是否大于設定面積閾值，大于則判定為洞形缺陷，小于則判定為線形缺陷或正常織物。

2.5.1 洞形缺陷

當判定為洞形缺陷后需進一步確定缺陷位置和消除噪聲點的干擾，本文提出的判定依據，如式(7)所示。

(7)

式中:DI為連通域I；SI為區域I的面積；SMAX為所有連通域中最大面積；k為面積比例系數。首先計算所有連通域面積DI，再依次判定連通域面積SI是否大于設定面積閾值SMAX×k，當SI大于SMAX×k時，判定其為缺陷，反之將此連通域面積判定為噪聲點。由于洞形缺陷通常具有缺陷集中且面積大小相似的特點，因此本文點選取k=0.8作為洞形缺陷面積比例系數。除去噪聲點的干擾后，在原圖中標定二值圖中所檢測到的缺陷位置，以驗證其準確性，效果如圖10所示。

圖10 洞形缺陷檢測結果Fig.10 Detection results of hole defects. (a) Area threshold filtering; (b) Defect original drawing verification

2.5.2 線形缺陷及正常織物

當最大連通域面積小于設定閾值時，僅能夠確定其為非洞形缺陷，既可能為線形缺陷，也可能為正常織物，由圖9(b)可知上述算法不能很好地檢測出線形缺陷，但在線形缺陷特征圖中缺陷區域和背景區域有著明顯差別，如圖11所示。可以看出在特征值圖11(b)中，織物背景區域處保留著紋理特征，而缺陷區域處存在著灰度值相似的線形，對于正常織物而言，因不存在缺陷，則整幅圖像為較清晰的紋理特征。

注：1—緯紗缺陷；2—經紗缺陷；3—正常織物。圖11 線形缺陷與正常織物特征值圖對比Fig.11 Linear defects are compared with the eigenvalue diagrams of normal fabrics. (a) Original image; (b) Eigenvalue image

基于上述特征可以區分出正常織物和線形缺陷，其步驟為：1)分別計算特征值圖像水平方向和垂直方向的方差值、方差均值及存儲最小方差值；2)通過對比水平方向和垂直方向的最小方差值大小，較小的方差值方向為缺陷方向；3)確定方向后，用該方向的方差均值與最小方差值做差，通過設定差閾值的方式來判斷是否為缺陷圖像，如果差值大于閾值證明圖像為線形缺陷，小于閾值則為正常織物圖像；4)如果確定為線形缺陷，則選取最小方差值的k倍作為閾值來確定缺陷位置，判定方法如公式(8)所示。

(8)

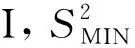
注：1—緯紗缺陷；2—經紗缺陷；3—正常織物。圖12 線形缺陷和正常織物方差閾值濾波結果Fig.12 Linear defects and normal fabric variance threshold filtering results. (a) Eigenvalue image of fabric; (b) Image of variance threshold filtering

從圖12可知，在經過方差閾值濾波之后，經、緯紗缺陷位置在方差閾值濾波圖中被準確定位，而在正常織物圖像中由于背景灰度方差值大于所設定的閾值，所以濾波圖灰度值為0。

3 實驗結果及分析

為驗證本文算法的可行性，實驗選用常見織物缺陷圖像作為樣本。其中包含破洞、毛洞、擦洞、缺經、缺緯、粗緯等十幾種缺陷，共250幅。織物圖像像素大小均為256×256。本文實驗中所檢測的算法是在Opencv環境下實現的，并在搭載 Intel Core i7處理器的Win10操作系統計算機上進行。

為對比算法效果，本文選用文獻[1]所述的加權中值濾波K-means算法、文獻[8]所述的窗口跳步形態學法進行對比，隨機選取5種典型洞形缺陷和線形缺陷檢測效果，3種織物缺陷檢測算法準確率和平均耗時參數如表1所示。

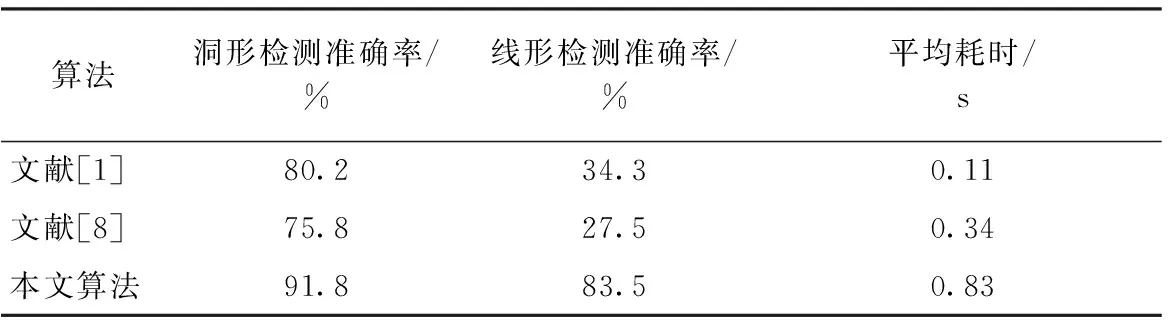
表1 3種織物缺陷算法比較Tab.1 Comparison of three fabric defect algorithms

圖13、14分別示出洞形缺陷和線形缺陷的部分檢測圖。為了更好地表示出織物缺陷位置，本文將算法檢測出的織物缺陷位置在輸入織物原圖上用方框標記突出顯示，如圖13(e)和圖14(e)所示。

注:1～5分別為5種典型洞形缺陷織物。圖13 洞形缺陷對比圖Fig.13 Comparison diagram of hole defects. (a) Original image; (b) Method of reference [1]; (c) Method of reference[8]; (d) Method of this paper; (e) Detection results of this paper

注:1～5分別為5種典型線形缺陷織物。圖14 線形缺陷對比圖Fig.14 Linear defect comparison diagram. (a) Original image; (b) Method of reference [1]; (c) Method of reference[8]; (d) Method of this paper; (e) Detection results of this paper

從表1可知，文獻[1]和文獻[8]在洞形缺陷檢測上準確率分別為80.2%和75.8%，而在線形缺陷檢測上僅有34.3%和27.5%。文獻[1]首先通過加權中值濾波模糊織物背景的同時使得織物缺陷處灰度值相等，然后通過K-means算法得出分割閾值，最后通過閾值分割背景和疵點，從圖13(b)所展示的檢測結果可知此算法對于洞形缺陷分割效果較好，尤其是疵點和背景灰度值相差較大的情況下，但對于織物缺陷處灰度值和背景灰度值相近，此算法則很難獲得一個較好的閾值來劃分背景和疵點，這一點對于對比度不高且缺陷分散的線形缺陷更加明顯，如圖14(b)所示，只有當線形缺陷和背景灰度值相差較大時才有較好的分割效果。文獻[8]則是通過迭代法獲取二值化閾值，然后通過形態學處理的方式來模糊背景并突出織物缺陷區域，此算法在洞形缺陷有較好的分割能力，但同樣難以檢測出背景和疵點對比度不高的缺陷。在線形缺陷中，由于缺陷狹長且灰度值與背景相似，此算法所設計的十字形態學核在進行卷積運算時會把缺陷同背景一起腐蝕，如圖14(c)第1組所示，缺陷位置因為和背景灰度值相似導致最后獲得的檢測圖未包含織物缺陷。

本文針對洞形缺陷特征圖及線形缺陷特征值圖特性，設計出雙算法進行檢測，在檢測洞形缺陷和線形缺陷中的準確率分別為91.8%和83.5%，平均耗時為0.83 s，相比于其他2種方法，本算法耗時稍高于其他2種算法，此問題可以通過對算法進行優化或者提升硬件條件等方法來減少檢測時間。但在疵點檢測準確率上，本文算法明顯高于其它兩種算法，證明此算法能有效地檢測出高對比度、低對比度、線形及洞形缺陷，能有效地去除噪聲點的干擾，正確地標定出織物缺陷區域，檢測效果最好。

4 結 論

本文針對常見的洞形缺陷和線形缺陷圖像特征進行研究，提出了基于奇異值分解的雙算法織物檢測的方法。利用奇異值分解和布爾差集運算模糊織物圖像背景區域并凸顯織物缺陷區域；再通過均值濾波、直方圖均值化、方差閾值濾波及形態學運算消除圖像噪聲點干擾初步獲得缺陷區域；最后用面積閾值和水平、垂直方向方差的方式區分線形缺陷、洞形缺陷及正常織物和確定缺陷位置。將本文方法得到的疵點檢測效果與其他檢測方法生成的疵點檢測效果圖進行比較，本文方法不僅能夠很好地檢測洞形缺陷，而且在線形缺陷上也有很好的表現，解決了不能有效地同時檢測洞形缺陷和線形缺陷的問題。實驗證明了本文算法的有效性和可靠性。