風電并網逆變器的雙閉環自抗擾控制策略研究

楊 霞，李 琛，楊路勇，胡延兵，段大偉

（國網山東省電力公司禹城市供電公司，山東 禹城 251200）

0 引言

并網逆變器是連接風電機組與電網的核心裝置，其工作性能直接影響風電系統的安全、穩定、高效運行等重要性能指標［1］。由于兩級式并網逆變器具有控制算法簡單、動態性能好等特點而被廣泛應用于風電并網的控制系統［2］，其中，網側逆變器對電能輸出的質量以及電網在多工況切換控制下都具有較大的影響，所以對網側逆變器控制策略研究是一個重要課題。

并網逆變器控制系統一般在dq同步旋轉坐標系下采用基于比例積分（Proportional Integral，PI）控制的電壓電流雙環控制系統進行設計，由于此控制系統中逆變器的d軸和q軸電流存在耦合現象，導致系統的抗擾能力弱。目前，針對dq軸電流耦合現象，許多新的控制算法被提出。文獻［3］采用反饋線性化理論進行解耦控制，方法復雜，魯棒性較差。文獻［4］使用加權平均電流控制實現dq軸電流解耦，但輸出電流與電網電壓存在相位差，需要增加補償裝置。文獻［5］采用擾動觀測器的偏差解耦控制方法，但對加速度形式的擾動存在穩態誤差。

針對強非線性、強耦合等復雜因素，已有研究提出了自抗擾控制技術［6-7］，一種不依賴于系統精確數學模型、無需測量系統所受擾動，以擴張狀態觀測器為核心，通過系統的輸入和輸出來觀測系統的實際運動，并對系統進行估計和補償的先進控制技術，然而，這種非線性方法理論分析困難，參數不易調節。為此，高志強教授提出了線性自抗擾控制（Linear Active Disturbance Rejection Control，LADRC）技術，對參數的調節以及理論分析都進行很大程度上的簡化，而且控制性能和非線性自抗擾控制效果相差不大，具有很好的工程實用價值［8］。文獻［9］將LADRC 應用到并網逆變器的電流環用于dq軸電流的解耦，而對電壓環的控制效果未進行說明和分析。

在傳統PI雙閉環控制的基礎上，結合LADRC 的思想，提出了基于一階LADRC 技術的新型雙閉環控制結構，以削弱dq軸電流之間的耦合關系，提高風電系統對電網電壓波動的抗擾性能。

1 風電并網逆變器系統

風力發電系統網側逆變電路原理如圖1所示。

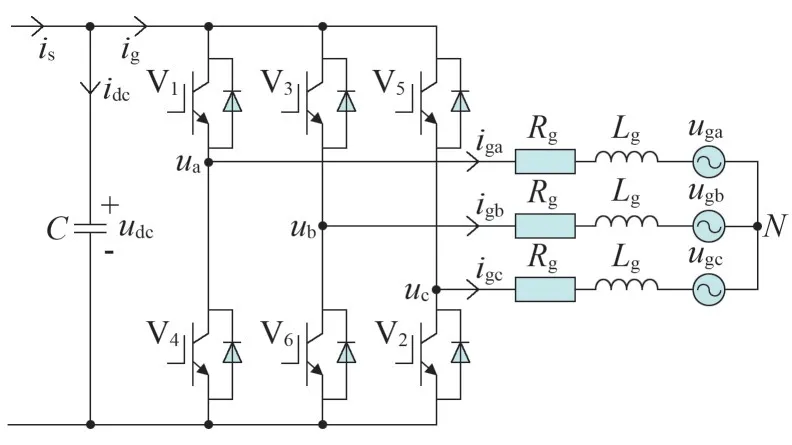
圖1 網側逆變電路的原理

1.1 風電并網逆變器數學模型

由圖1，可計算分析出公式（1）。

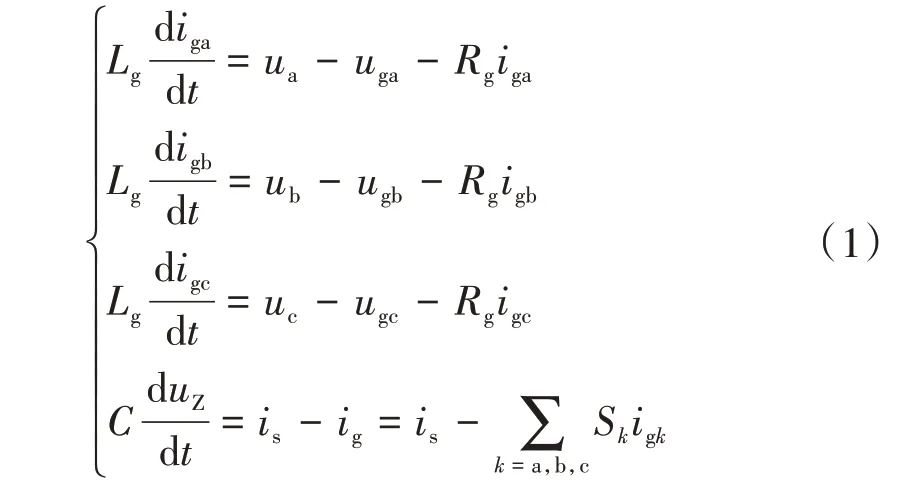
式中：ua、ub、uc為逆變器交流側對N點的相電壓；uga、ugb、ugc為電網電壓；iga、igb、igc為網側逆變器輸出電流；is為機側逆變器輸出電流；ig為流入網側逆變器的直流電流；Lg為網側濾波電感；C為逆變器側電容；Sk(k=a，b，c)為開關函數，Sk=0 代表k相下橋臂處于導通狀態，Sk=1 代表k相上橋臂處于導通狀態。

三相靜止坐標系下逆變器的數學模型中包含時變的交流量，不利于控制系統的設計，通過Park變換可將交流量變換為直流量，網側逆變器在兩相旋轉坐標系下的數學模型為

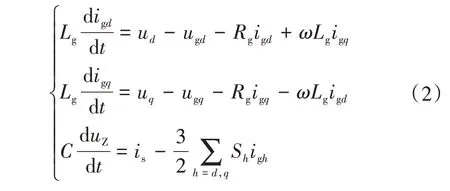
式中：ud、uq與igd、igq分別為網側逆變器輸出電壓、電流在d、q軸上的分量；ugd、ugq為電網電壓在d、q軸上的分量；ω為電網電壓的基波角速度；Sh(h=d，q)為開關函數在d、q軸上的分量。

1.2 逆變器控制系統

由式（2）可知，d軸及q軸電流分量是耦合的，需要進行解耦以簡化控制器的設計［10］。

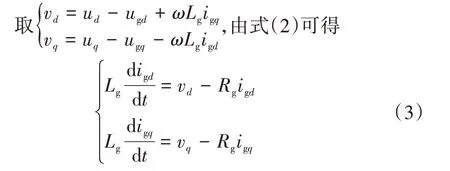
由式（3）可知，當以vd、vq作為等效電流控制變量時，d軸和q軸電流是獨立控制的。電流內環采用PI調節器

式中：kpi、kii分別為電流環的比例系數及積分系數；id為d軸電流實際值；iq為q軸電流實際值；id_ref為d軸電流參考值；iq_ref為q軸電流參考值。

考慮到電流環d軸和q軸控制的對稱性，以d軸電流調節器的設計為例，針對脈寬調制（Pulse Width Modulation，PWM）的小慣性和電流內環信號采樣的延遲，可設計出電流內環結構，如圖2所示。

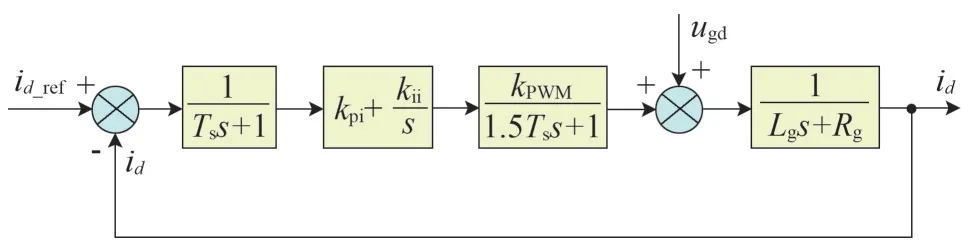
圖2 d軸電流環

圖2 中，kPWM為橋路PWM 等效增益，Ts為電流采樣周期，PI 調節器寫成零極點形式，即kpi+kii=kpi(τis+1)(τis)，其中τi為電流環時間常數。將Ts與小時間常數0.5Ts合并以簡化分析，得電流內環的開環傳遞函數［11］

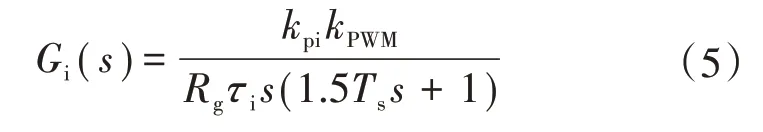
按典型I型系統參數整定關系，取系統阻尼比為0.707，可求得PI參數

將式（5）、式（6）聯立并忽略s2項，得到電流內環等效簡化傳遞函數為

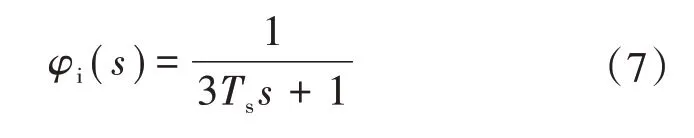
式（7）表明電流環可近似等效為時間常數為3Ts、良好跟隨性和較快動態響應的一階慣性環節，但系統抗擾能力較差。

在電流內環解耦控制的基礎上再引入直流電壓反饋和PI 調節器，就構成了三相電壓型逆變器的雙閉環控制系統，原理如圖3所示。

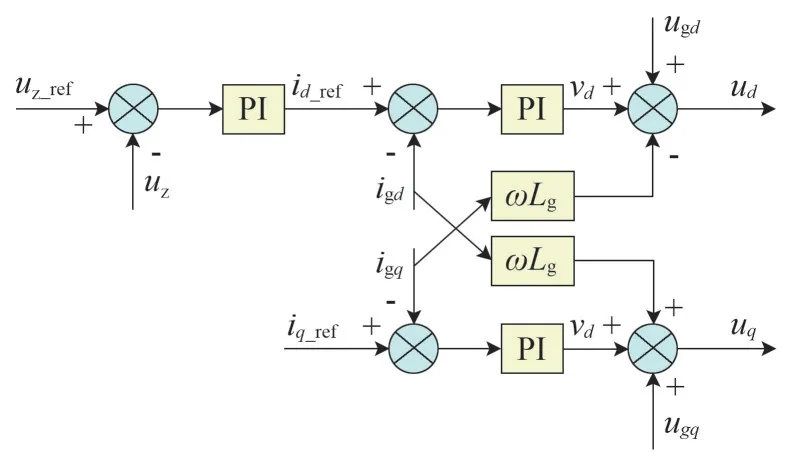
圖3 雙閉環控制系統

2 一階LADRC的設計

2.1 一階LADRC的設計原理

LADRC 能將外擾、耦合等視為總和擾動，通過線性擴張狀態觀測器（Linear Extended State Observer，LESO）進行估計和補償，將系統補償為純積分串聯型，再用一定的線性狀態誤差反饋控制律（Linear State Error Feedback，LSEF），將其改造成期望的閉環系統，獲得期望的閉環動態特性。因此LESO 的設計在LADRC 的設計中占有非常重要的地位，是自抗擾控制器的核心［12-13］。因此，被控對象的微分方程可描述為

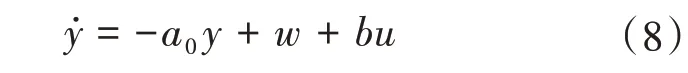
式中：u和y分別為系統的輸入和輸出；w為未知擾動；a0為系統的參數；b為未知的輸入控制增益，可對b進行估計，假設估計值為b0。令x1=y，定義f(y，w)=-a0y+w+(b-b0)u為系統廣義擾動，包括系統中所有的不確定因素和外部擾動，并令x2=f(y，w)，h=f(y，w)，可得系統的狀態方程為

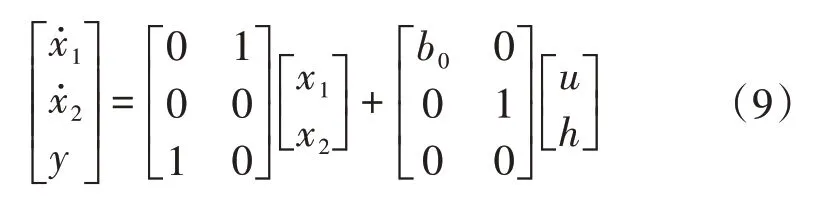
建立二階LESO為

式中：z1為y的跟蹤信號；z2為跟蹤總和擾動信號；β1、β2為觀測器的系數。

取系統的擾動補償環節為

忽略z2對f(y，w)的估計誤差，式（9）可簡化為一個積分環節

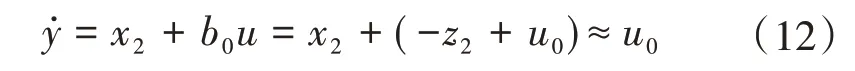
由于沒有對狀態的微分進行觀測，故LSEF 采用比例控制為

式中：kp為比例控制增益；v為輸入信號。由式（12）—式（13）得閉環系統的傳遞函數為

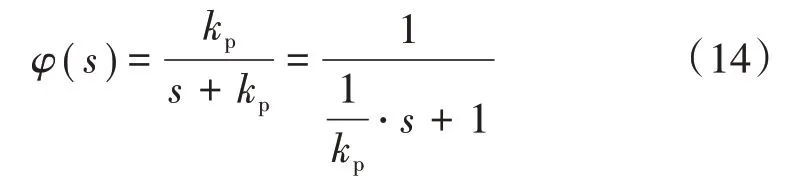
由式（14）知，比例控制的帶寬ωc=kp，選取合適的比例增益可使系統達到穩定。

當一階線性自抗擾控制器由LESO、LSEF 與擾動補償環節構成時，其結構如圖4所示。

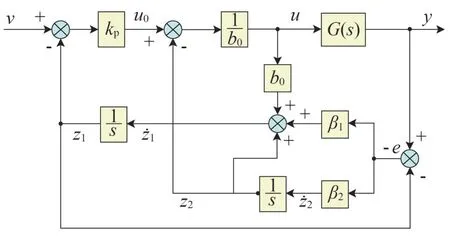
圖4 一階線性自抗擾控制器

根據極點配置，將式（10）的極點配置在觀測器的帶寬ω0上，即

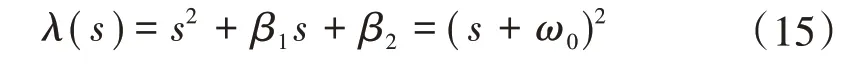
可得二階LESO的增益為

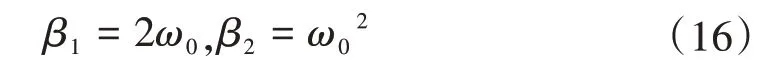
因此，一階LADRC可簡化為對ω0、ωc的控制。

2.2 基于一階LADRC電流內環控制系統的設計

考慮到系統受擾動時，并網點電壓會受到影響，進而導致電流內環的參考輸入信號中含有擾動成分，影響LADRC 的控制性能，基于此仍采用傳統雙閉環中將電網電壓作為前饋補償的思想以提高系統的動態性能。將dq軸電流間的耦合等因素作為總擾動，通過LESO與擾動補償環節進行估計和補償。以d軸電流為例進行設計，根據式（2）可得電流內環控制系統對應的狀態空間為

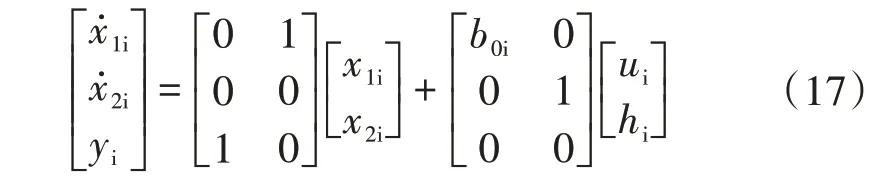
式中：b0i=1g；x1i為d軸電流實際值；yi為電流環的輸出；ui為電壓外環輸出的d軸參考電流id_ref；x2i為LESO 擴張出的新的狀態變量，用來描述電流環的總擾動，包括系統內部不確定性和外部擾動，記為fi=，并且=hi。

根據式（10）、式（16）可得電流內環的二階LESO為

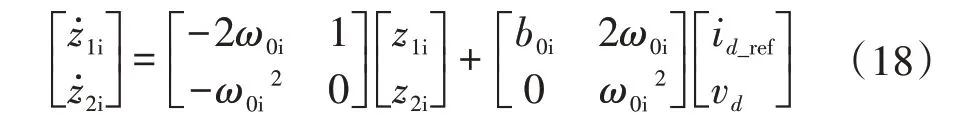
式中：z1i為電流環輸出的估計值；為z1i的微分值；z2i為電流環總擾動的估計值為z2i的微分值；ω0i為電流環觀測器的帶寬。

比例控制的LESF以及擾動補償環節為

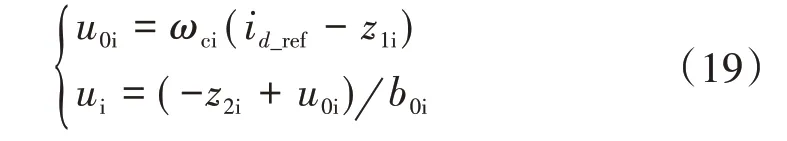
式中：ωci為電流環控制器的帶寬；u0i為電流環控制器的輸出。

2.3 基于一階LADRC電壓外環控制系統設計

電壓外環采用LADRC 時，首先建立其對應的LESO，根據式（4）可得電壓外環對應的狀態空間表達式為

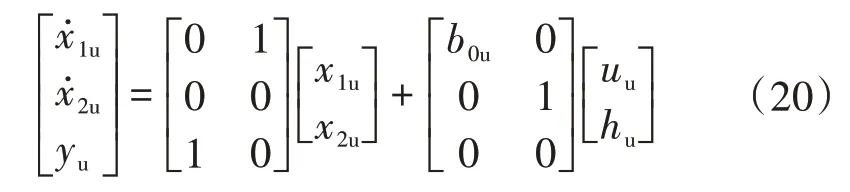
式中：b0u=3/（2C）；x1u為母線電壓實際值；yu為電壓環的輸出；uu為直流母線電壓的參考值；x2u為LESO 擴張出的新的狀態變量，用來描述電壓環的總擾動，記為fu=is/C-3Sqigq/（2C），并且=hu。

電壓外環的二階LESO為

式中：z1u為電壓環輸出的估計值為z1u的微分值；z2u為電壓環總擾動的估計值；為z2u的微分值；ω0u為電壓環觀測器的帶寬。選取合適的ω0u，可使z1u、z2u快速的跟蹤udc以及系統的總擾動。

LESF以及擾動補償環節為

式中：ωcu為電壓環控制器的帶寬；u0u為電壓環控制器的輸出。

據上述分析，得網側逆變器控制系統如圖5所示［14-18］。

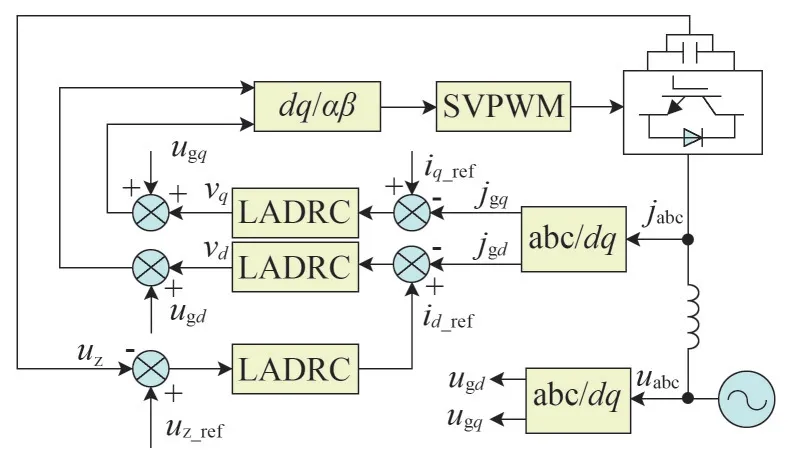
圖5 并網逆變器控制系統

3 仿真分析

利用MATLAB/Simulink 對風電并網系統進行仿真，系統部分參數：永磁直驅電機額定功率1.5 MW，額定電壓690 V，直流側母線電壓、電容分別為1 070 V、240 μF，網側進線等效電阻0.942 Ω，網側濾波器電感、電容為147 μF、120 μF。兩種控制方式下，控制器的參數如表1所示。

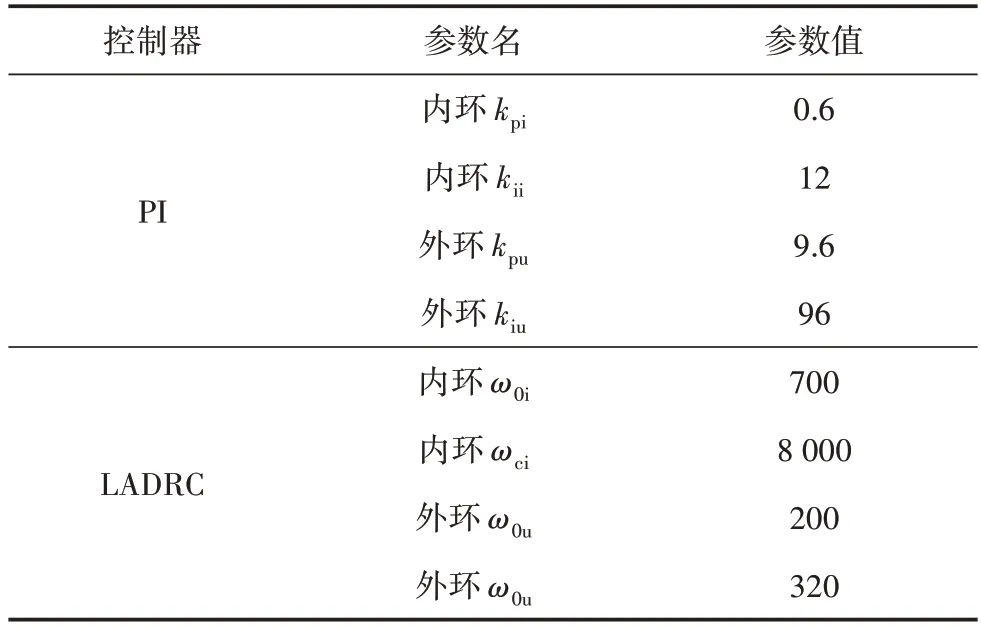
表1 控制器參數

3.1 穩態性能仿真對比

圖6 所示分別為風電系統穩態運行時，電流內環d、q軸輸出電流實際值、直流母線電壓在傳統PI雙閉環控制與LADRC 雙閉環控制中的波形對比。可以看出，采用LADRC 雙閉環控制，d、q軸實際輸出電流的穩態精度更高，直流母線電壓跟蹤給定參考值的響應速度更快。

圖6 穩態時仿真波形

3.2 解耦控制仿真對比

圖7 所示分別為d軸參考電流在0.6 s 時在原參考電流的基礎上增加1 000 A，在1 s時又減少500 A，d軸和q軸輸出電流、直流母線電壓波形對比。

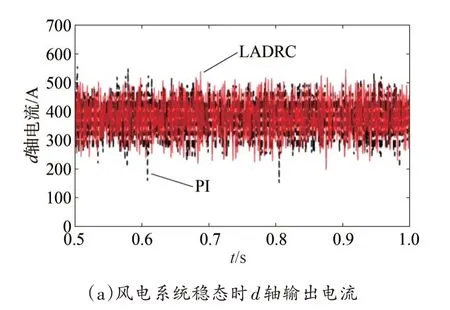
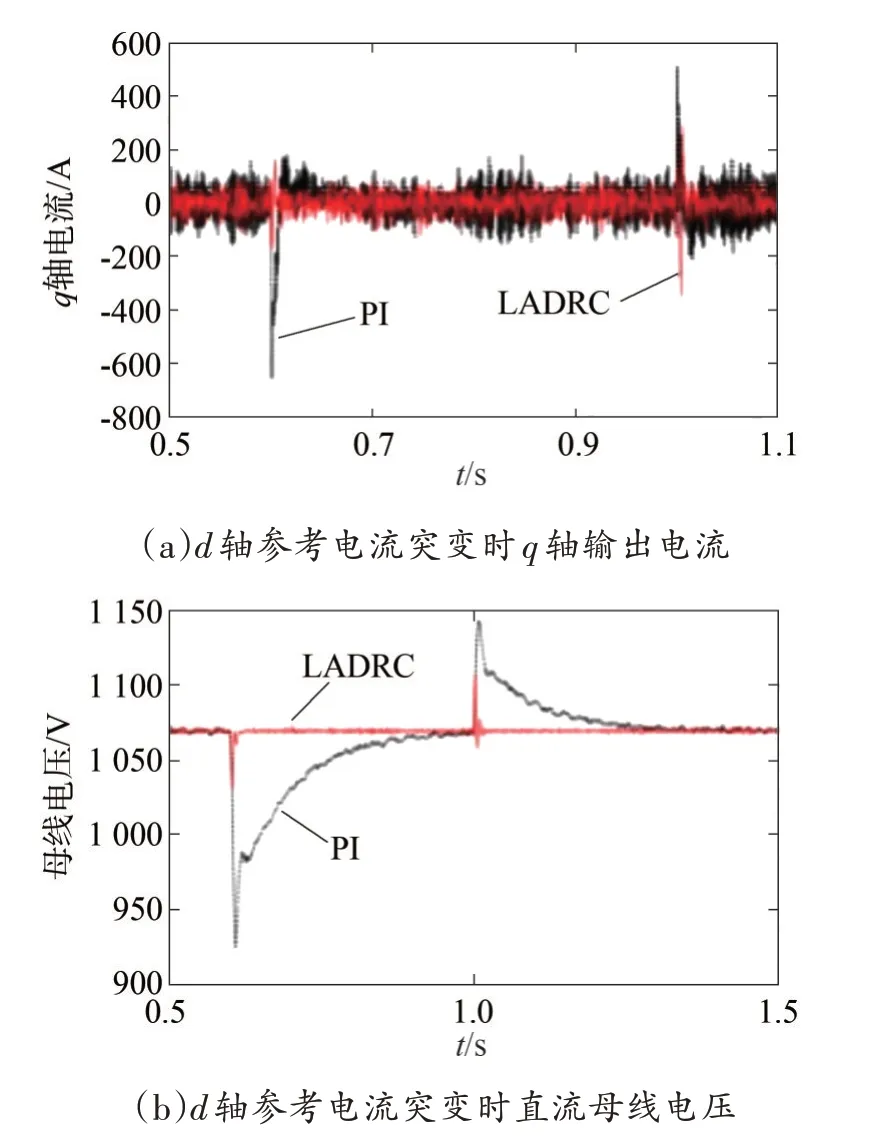
圖7 d軸參考電流突變時仿真波形

圖8 所示分別為q軸參考電流在0.6 s 時從0 階躍至1 000 A，在1 s時又從1 000 A階躍至500 A時，q軸和d軸輸出電流、直流母線電壓波形。表2 為兩種控制方式下，直流母線電壓的動態性能指標。

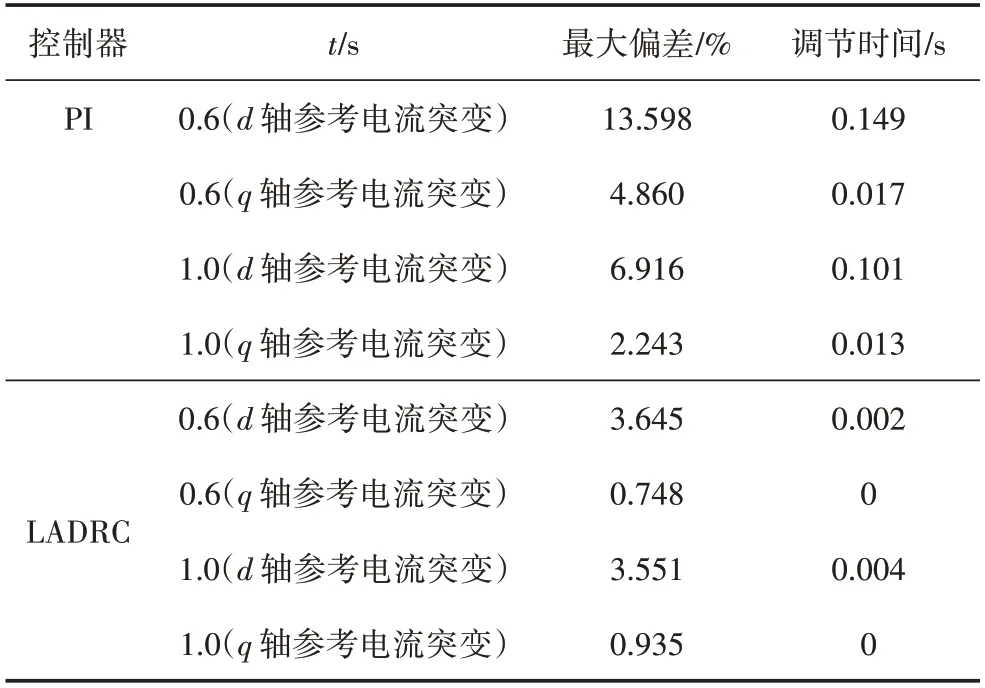
表2 參考值突變時兩種控制的動態性能指標

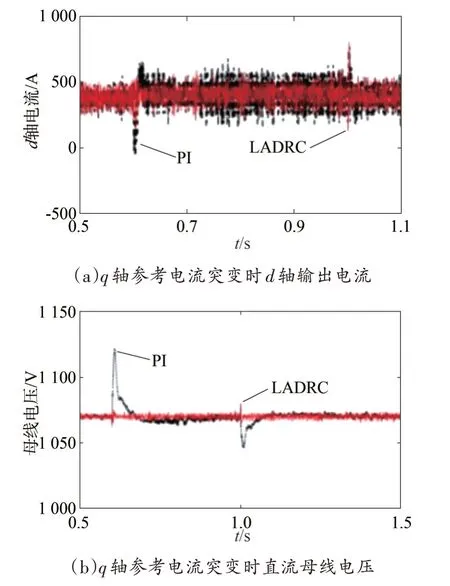
圖8 q軸參考電流突變時仿真波形

由圖7、圖8 和表2 可知，d軸或q軸參考電流突變時，對應q軸或d軸的輸出電流采用LADRC 雙閉環控制時會在突變瞬間產生較大的波動，之后q軸或d軸的輸出電流基本保持原來的穩定狀態運行，直流母線電壓在參考電流突變時會產生波動，暫態過渡過程時間極短。而采用傳統的PI 雙閉環控制時，d軸或q軸參考電流突變會導致q軸或d軸的輸出電流產生較大波動，直流母線電壓會產生較長的過渡過程時間，說明采用傳統的PI控制d軸和q軸仍存在耦合關系，而使用LADRC 策略基本實現電流解耦，提高系統的魯棒性。

3.3 抗擾性能仿真對比

圖9 分別為電網電壓在0.6 s 時對稱跌落60%，在1 s 時故障恢復，d軸和q軸輸出電流、直流母線電壓、并網點電壓在兩種控制方式下的波形對比。

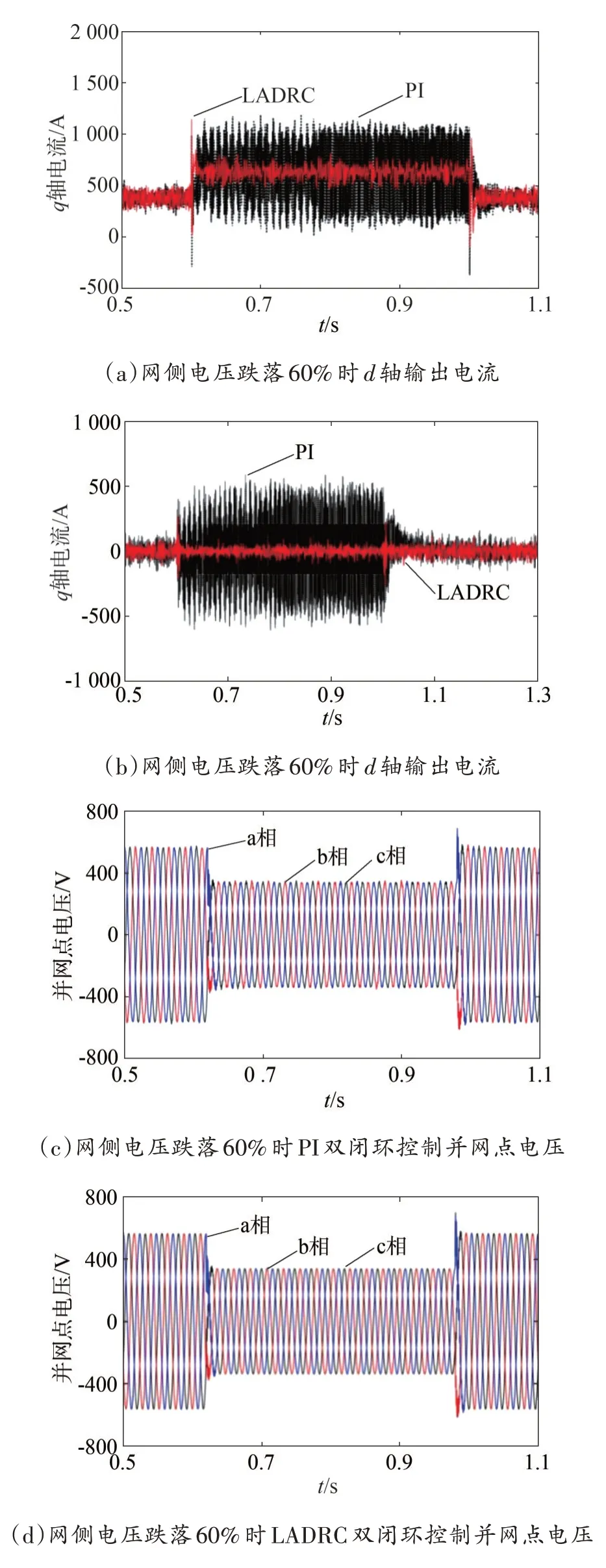
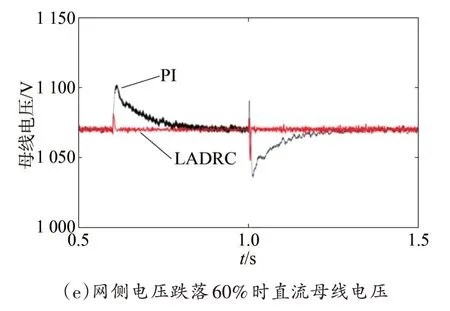
圖9 網側電壓跌落60%

由圖9 知，電網電壓發生故障時，采用傳統PI雙閉環控制時d軸和q軸輸出電流會產生很大的波動，導致控制器控制效果變差［19-20］，影響并網點電壓的波形，使直流母線電壓的控制受到影響。兩種控制方式下，直流母線電壓的動態性能指標如表3。

表3 電網電壓突變時兩種控制的動態性能指標

綜上可得，基于LADRC 的雙閉環控制系統能夠實現d軸和q軸參考電流之間的解耦，且在穩態性能與動態性能特別是抗擾性能上明顯優于傳統的PI雙閉環控制效果。如在電壓跌落60%時，PI控制技術的最大偏差為2.991%，而LADRC 控制技術的偏差僅僅為1.121%，后者在性能上要遠遠優于前者。所以，通過上述一系列的理論、仿真分析可清楚說明本文針對風電并網逆變器所設計的控制器具有一定的優越性。

4 結語

以三相電壓型PWM 逆變器為研究對象，建立其數學模型以及傳統PI 雙閉環控制策略，在此基礎上對一階自抗擾控制器進行了推導與分析，提出了基于LADRC 的電壓電流雙閉環控制策略，內環用于對d軸和q軸電流進行解耦，外環用于提高系統的抗擾性及響應速度。仿真結果表明，基于LADRC 的電壓電流雙閉環控制策略在解耦效果、動態響應速度、抗擾性能方面均優于傳統的PI 雙閉環控制效果。由此可知，在大型風電并網控制系統中利用本文所設計的控制器，其控制穩定性上可能會優于傳統的控制技術。

由此可以說明，新型雙閉環控制策略在并網逆變器的控制方面具有很好的控制效果。那么，在接下來的研究中就可以把理論設計用于實際制造，把本文所設計的新型雙閉環控制策略用于電力線桿警示標識自動噴涂裝置的設計中，對自動噴涂裝置進行深一步的優化與改進，提高該裝置在多場合、多環境、多條件下的廣泛應用，進一步提高實際工作過程中的效率，真正意義上的達到自動裝置的智能化，為電力事業的發展做出貢獻。

本文的控制器在實驗仿真時只是針對風電并網逆變器進行了低電壓穿越故障的設計，在接下來的研究中將具體的設計風機的加減載、高電壓穿越、滿載等一系列工況來對本文所設計的控制器進行有效的驗證。