基于機器學習對串聯排隊系統等待時間的預測①

衛安妮， 趙寧， 張志堅

昆明理工大學 理學院，昆明 650500

排隊網絡模型在流水生產線、 交通運輸、 計算機通信等領域應用十分廣泛，吸引了眾多學者的關注． 串聯排隊系統是排隊網絡的基本結構[1]，顧客在一個站接受服務后按照一定的規則接受下一個站的服務，研究該系統對深入分析復雜的排隊網絡具有重要意義．

串聯排隊系統的研究最早可追溯到20世紀50年代，文獻[2-5]研究了具有馬爾可夫性的串聯排隊系統的平均等待時間等性能指標． 隨后，關于滿足馬爾可夫性的串聯排隊系統得到了廣泛研究． 然而，實際生活中排隊系統一般不滿足馬爾可夫性，這導致串聯排隊系統的性能很難用解析的方法來求解，通常使用近似方法進行分析． 文獻[6]提出了排隊網絡分析方法(queueing network analysis，QNA)研究不滿足馬爾可夫性的串聯排隊系統． 文獻[7]利用到達過程和服務時間的一階矩和二階矩的近似提出了排隊網絡方法(queueing network，QNET)估計顧客的平均逗留時間． 文獻[8]基于分解的方法使用聯合矩對MAP/MAP/1排隊網絡進行了分析． 文獻[9]同樣基于分解算法提出魯棒排隊網絡分析器算法(robust queueing network analyzer，RQNA)近似開排隊網絡的穩態性能． 文獻[10]使用固有比的方法近似串聯排隊系統的平均排隊時間． 文獻[11]采用指標比研究M/G/1-G/1串聯排隊系統的平均等待時間． 文獻[12]提出三階近似的方法分析GI/G/1-G/1串聯排隊系統的平均等待時間． 文獻[13]基于泛函重對數律和重對數律極限的方法，分析GI/G/1-G/1串聯排隊系統的性能指標的波動程度．

近年來，基于機器學習分析排隊系統引起一些學者的關注． 文獻[14]利用支持向量機(support vector machine，SVM)對排隊系統中到達和服務時間的概率密度函數進行分類和識別，并通過支持向量回歸(support vector regression，SVR)解決概率密度函數回歸的問題． 文獻[15]使用機器學習的方法對患者的治療數據進行預測，根據預測的治療時間推斷其等待時間，結果表明隨機森林模型為每日治療時間提供了最佳的預測． 文獻[16]使用分位數、 普通最小二乘(ordinary least square，OLS)回歸以及機器學習算法對某醫院患者的平均等待時間進行預測，結果表明套索回歸(lasso regression，Lasso)和分位數回歸方法的準確率更高． 文獻[17]使用交通模擬器對神經網絡進行訓練，得到一個自適應交通系統． 文獻[18]使用神經網絡方法對銀行排隊的等待時間進行預測，證明機器學習是預測排隊等待時間的一種可行方法． 文獻[19-20]使用高斯過程回歸預測單服務器和多服務器排隊網絡的平均逗留時間．

在日常生活中，串聯排隊系統廣泛存在于生產系統等領域． 串聯排隊系統中站與站之間存在關聯性，上游站的輸出過程是下游站的輸入過程，對于不滿足馬爾可夫性的排隊系統，下游站的到達過程很難用解析的方法分析． 本文考慮具有兩個站的串聯排隊系統，其到達過程和服務時間均服從一般分布，通過模擬串聯排隊系統的平均等待時間生成訓練集，使用機器學習預測一般串聯排隊系統的平均等待時間，并與近似方法進行比較．

本文結構如下： 第1節描述了兩個站的串聯排隊模型；第2節介紹了常見的線性和非線性機器學習回歸算法；第3節利用機器學習的方法預測串聯排隊系統的平均等待時間；第4節將機器學習中的XGBoost算法與其他近似方法進行比較；第5節為結論．

1 模型描述

本文研究圖1所示的串聯排隊系統，該系統由兩個站串聯而成，每個站有一個服務器，并且服務器前的緩沖區無限大． 顧客的到達過程為更新過程，顧客到達系統后依次在每個站接受服務，服務完成后離開系統． 系統的服務規則為先到先服務(first come first served，FCFS)，每個服務器的服務時間服從一般分布．

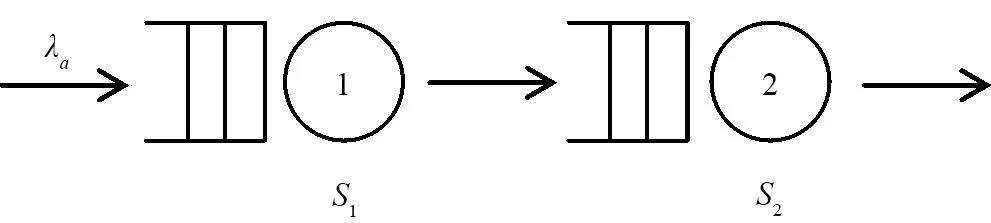
圖1 兩個站的串聯排隊系統

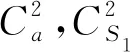
其中E(X)和D(X)分別表示到達時間間隔的期望和方差，E(Si)和D(Si)，i=1，2分別表示第1個站和第2個站的服務器的服務時間的期望和方差． 串聯排隊系統中第1個站和第2個站的服務強度分別記為ρ1和ρ2，且

ρ1=λaE(S1)

ρ2=λaE(S2)

令ρ=max{ρ1，ρ2}． 串聯排隊系統中第1個站和第2個站的平均排隊時間分別記為W1和W2．

2 機器學習回歸算法

近年來，機器學習快速發展，廣泛應用于數據挖掘、 人工智能、 醫療保健、 排隊等領域． 與傳統回歸方法相比，機器學習能夠分析和挖掘數據中的規律，并對新的樣本進行預測，適合處理復雜的回歸問題． 下面介紹機器學習中常見的回歸算法．

2.1 線性回歸模型

機器學習中常見的線性回歸模型為多元線性回歸(multiple linear regression，MLR)、 嶺回歸(ridge regression，Ridge)以及套索回歸(lasso regression，Lasso)． 線性回歸模型屬于一種監督學習算法，研究兩個隨機變量之間的線性關系． 該模型可表示為

Y=Xβ+ε

其中：X表示線性回歸模型的自變量集合，Y表示線性回歸模型的因變量，β表示偏回歸系數，ε表示模型擬合后每一個樣本的誤差項．

為了求解線性回歸模型的參數，將該模型的目標函數表示為[16]

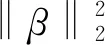
2.2 非線性回歸模型

對于比較復雜的非線性回歸模型，需要在因變量和多個自變量之間構建復雜的非線性關系． 機器學習的非線性回歸算法主要包括K近鄰(k-nearest neighbor，KNN)、 支持向量機(support vector machine，SVM)、 決策樹(decision tree，DT)、 隨機森林(random forest，RF)、 梯度提升樹(gradient boosting decision tree，GBDT)以及極端梯度提升(extreme gradient boosting，XGBoost)算法． 本文將以上非線性回歸算法分為3類： 遞歸劃分方法、 黑箱方法和集成學習方法[22]．

遞歸劃分方法主要包括決策樹(DT)算法． 該算法按照一定的規則持續拆分數據，每次將數據劃分為兩個相對一致的子集，直到達到目標，從而形成樹狀結構，直觀反映變量的重要性，但該算法結構不穩定，容易產生過擬合的現象．

黑箱方法包括K近鄰算法(KNN)以及支持向量機(SVM)算法． 這類算法的輸入到輸出過程是通過一個模糊的“箱子”進行處理． KNN通過比較已知樣本和預測樣本的相似度，尋找最相似的k個樣本作為未知樣本的預測． 采用多重交叉驗證法選取最佳k值． SVM利用某些支持向量構成的“超平面”，將不同類別的樣本點進行劃分，SVM算法與其他單一的算法相比，能夠將低維不可分的空間轉化為高維的線性可分空間，具有較高的預測準確性，但其最大的缺點是容易受共線性影響，運算成本高． 這類方法對數據缺失較敏感，處理大規模數據的效率較低．

集成學習方法通過選擇某種結合策略將若干弱學習器集合起來，以得到一個預測效果較好的強學習器． 隨機森林(RF)、 梯度提升樹(GBDT)以及極端梯度提升(XGBoost)算法是一類以決策樹(DT)為基學習器的集成學習算法． RF采用多棵決策樹的投票機制，即將多棵樹的回歸結果進行平均，最終得到樣本的預測值． 類似的，GBDT也是通過對多棵樹的結果進行綜合，不同的是每棵樹是從之前所有樹的殘差中學習的，并以新樹每個葉子的信息增益來進行最后的全局預測． XGBoost采用了隨機森林的思想，作為升級版的GBDT算法，XGBoost使用損失函數的一階導和二階導作為殘差的近似值，而GBDT僅利用損失函數的一階導作為殘差的近似值． 集成學習方法通常優于單一的回歸方法，但預測速度明顯下降，隨著學習器數目的增加，所需的存儲空間也急劇增加[23]．

通常采用線性回歸模型以及非線性回歸模型進行預測時，需要將不同模型的運行時間成本和準確率進行對比分析，從中選擇合理的模型進行預測． 本文將準確率作為衡量標準，選擇較優的模型對串聯排隊系統的平均等待時間進行預測．

3 基于機器學習預測平均等待時間

3.1 訓練集數據

為了生成機器學習所需的訓練集數據，首先對串聯排隊系統進行模擬，得到不同參數下串聯排隊系統的平均等待時間．

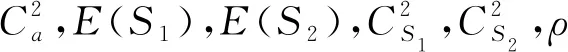
表1 訓練集的參數

對于每個串聯排隊系統，模擬運行30個樣本，每個樣本取第400 001個顧客到600 000個顧客在第1個站和第2個站的等待時間的平均值分別作為第1個站和第2個站的平均等待時間，其中平均等待時間的置信水平大于95%，保證了模擬數據的可靠性．

3.2 數據預處理

在對訓練集數據進行建模分析之前，需要對數據進行預處理以滿足模型的要求． 對于等待時間非常小的數據，即使預測值只有微小的偏差，其相對誤差也會非常大，造成整體的平均誤差偏大，影響預測效果． 因此，本文選取第1個站和第2個站的平均等待時間均大于0.1的數據進行分析． 從圖2和圖3的分布來看，模擬得到的串聯排隊系統的第1個站和第2個站的平均等待時間均呈現嚴重的右偏現象，為了滿足機器學習模型的數據要求，提高模型精度和訓練效率，本文對第1個站的平均等待時間W1和第2個站的平均等待時間W2分別進行對數處理，令

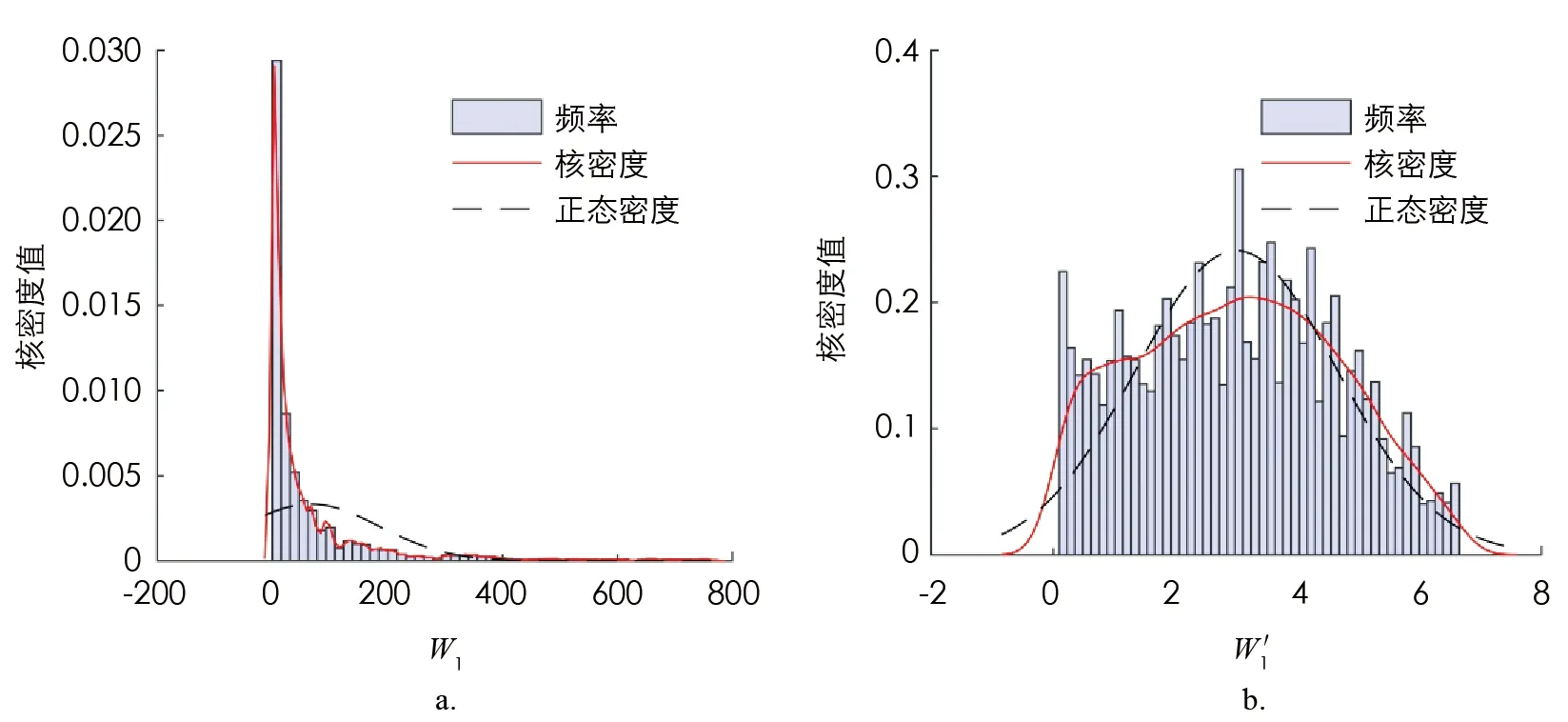
圖2 第1個站的平均等待時間W1及其對數變換W′1

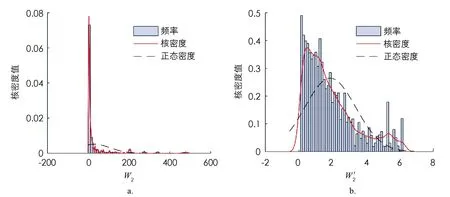
圖3 第2個站的平均等待時間W2及其對數變換W′2

W′i=log(Wi+1)，i=1，2

計算模擬得到的數值Wi和W′i(i=1，2)的核密度如圖2，3所示． 從圖中可知經過對數處理后，W′1的分布近似服從正態分布，W′2的右偏現象明顯有所緩解，W′i，i=1，2的值域均縮小到[-2，8]之間，采用W′i加快了梯度下降求最優解的速度，即機器學習訓練的速度．

3.3 基于線性回歸模型預測平均等待時間

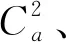
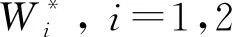
表2 線性回歸模型的最佳λ值

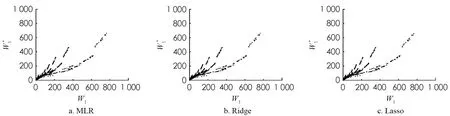
圖4 基于線性回歸模型對第1個站平均等待時間的預測

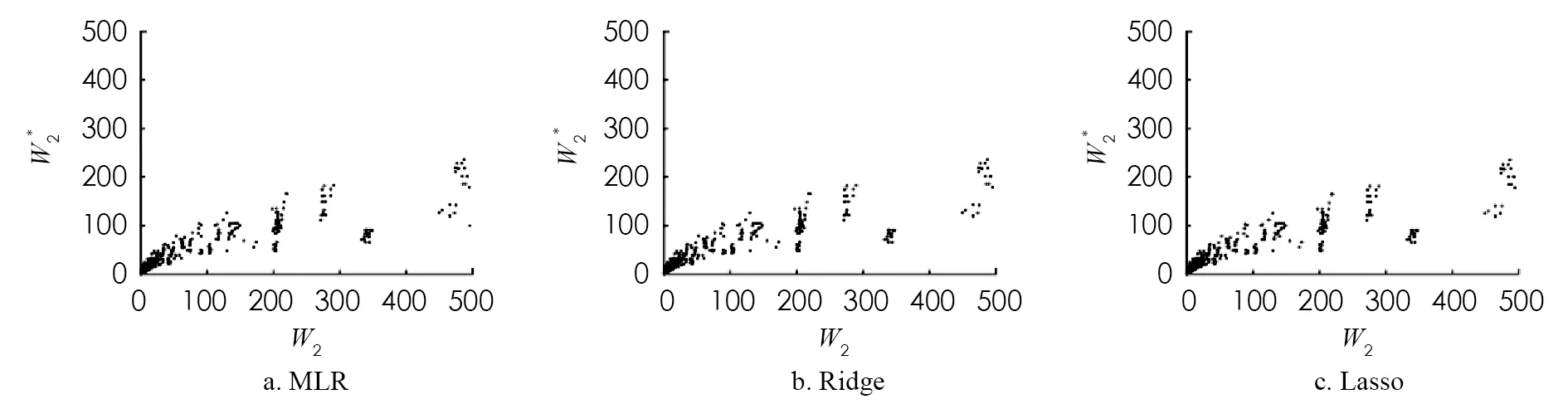
圖5 基于線性回歸模型對第2個站平均等待時間的預測

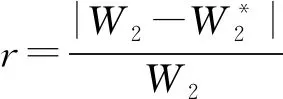
3.4 基于非線性回歸模型預測平均等待時間

下面使用非線性回歸模型對串聯排隊系統的平均等待時間進行預測，其中包括K近鄰(KNN)、 支持向量機(SVM)、 決策樹(DT)、 隨機森林(RF)、 梯度提升樹(GBDT)以及極端梯度提升(XGBoost)算法． 大多數機器學習算法都需要對參數進行設置，參數設置不同，學習得到的模型性能往往有顯著的差異． 因此，使用非線性回歸模型對平均等待時間進行預測時，需要對參數調優． 為了提高參數優化的效率，使用10重交叉驗證的方法調整參數，并通過網格搜索找到最佳的參數組合． 各模型參數的范圍和最優值如表3所示，其中參數最優值(x1，x2)中x1和x2分別表示預測W1和W2所設定的模型參數．

表3 模型的參數范圍和最優值

對于上述非線性回歸模型，使用最優的參數組合對訓練集數據進行學習，并對測試集進行預測． 非線性回歸模型預測的第1個站和第2個站的平均等待時間及其模擬值如圖6，7所示． DT，RF，GBDT以及XGBoost算法的預測效果明顯優于KNN和SVM算法，這是由于RF，GBDT和XGBoost是基于DT的集成學習算法，結合了對所有弱學習器的預測，優于單一的學習器．

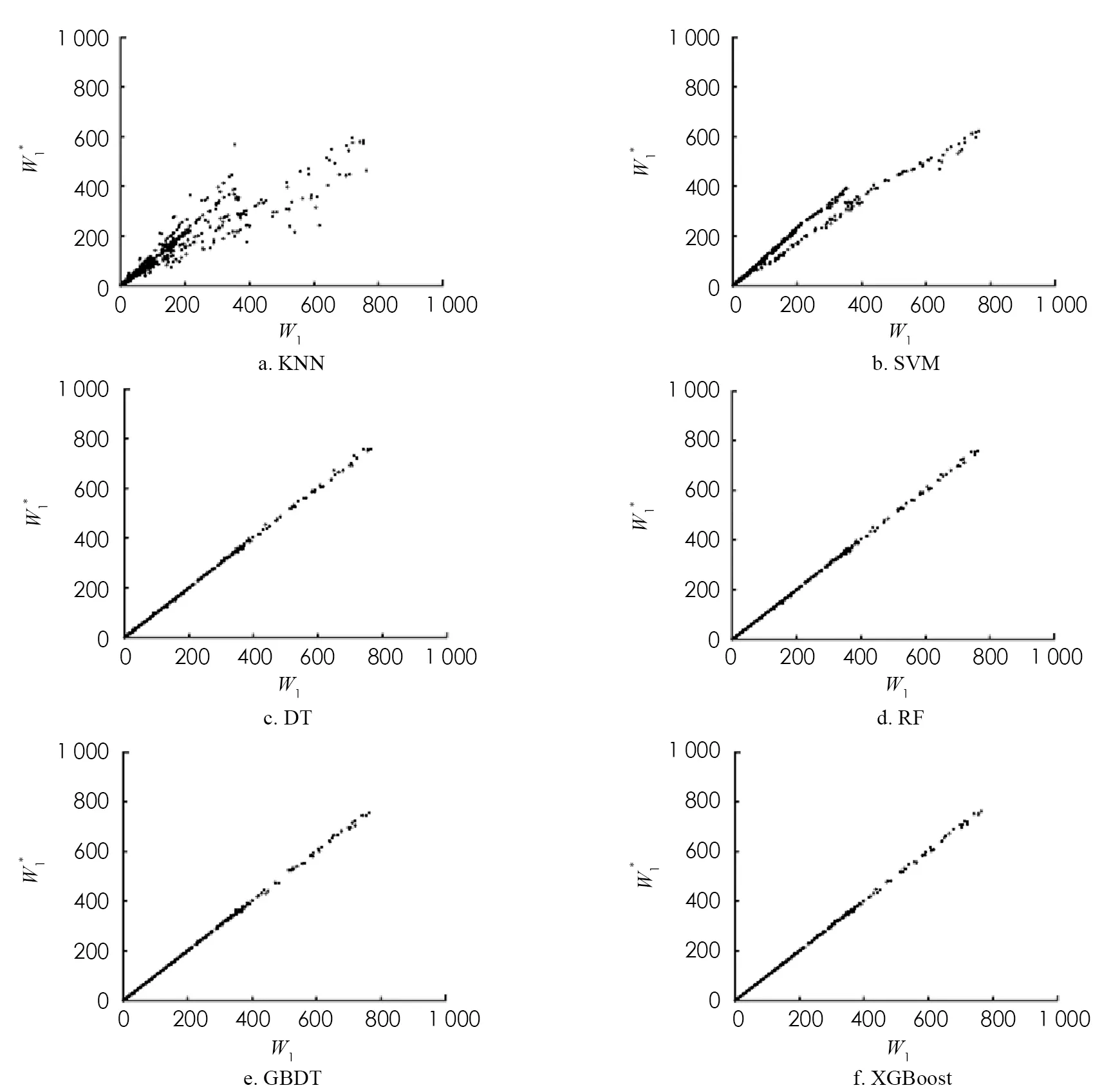
圖6 基于非線性回歸模型對第1個站平均等待時間的預測

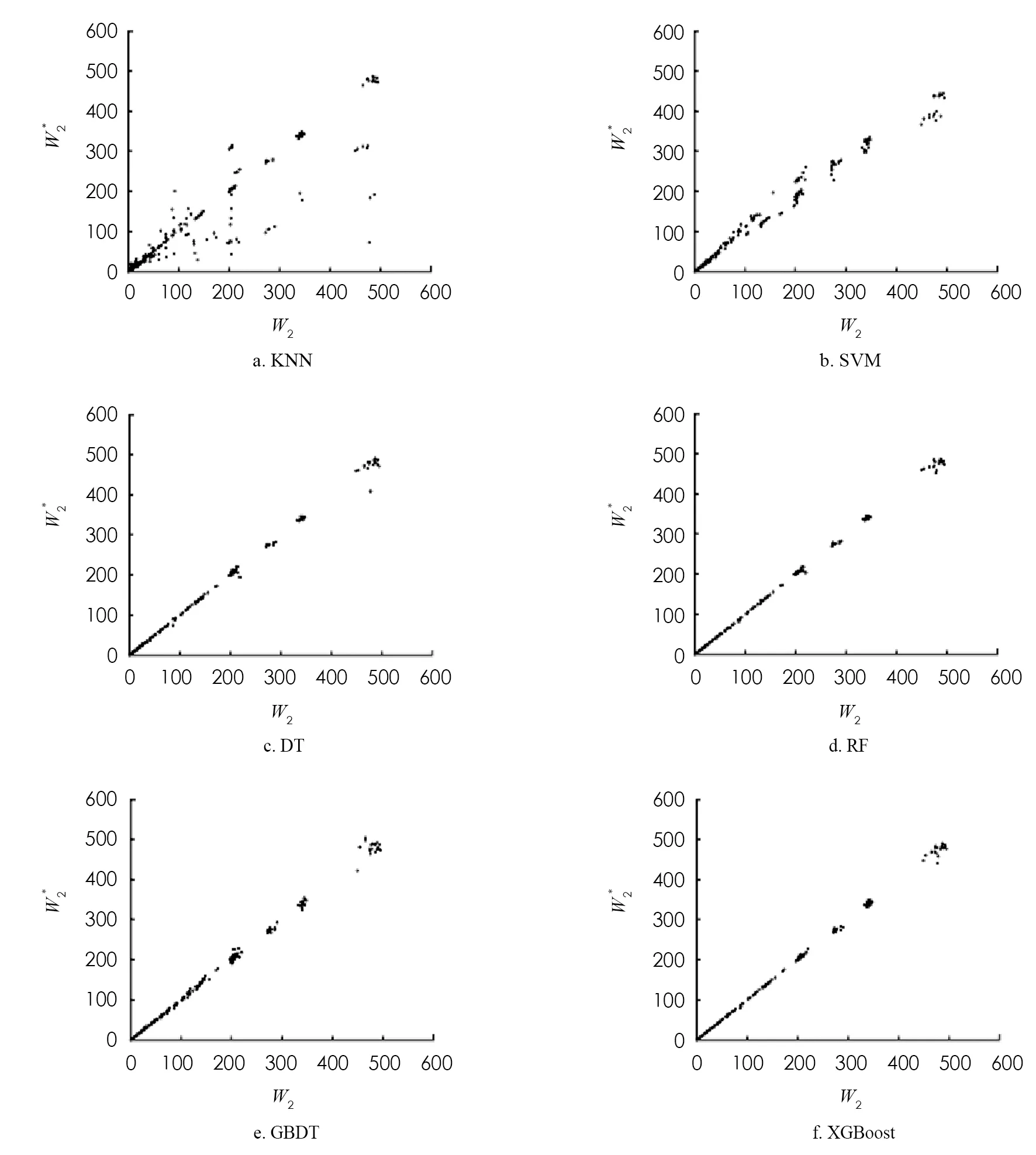
圖7 基于非線性回歸模型對第2個站平均等待時間的預測

為了比較DT，RF，GBDT以及XGBoost算法的預測效果，將平均相對誤差r作為模型的評價標準，4種模型的第1個站的平均等待時間的平均相對誤差分別為3.42%，2.33%，2.79%，1.60%，第2個站的平均等待時間的平均相對誤差分別為8.34%，4.13%，3.34%，1.86%． 實驗結果表明，DT算法對于第2個站的平均等待時間的預測效果較差，XGBoost算法對第1個站和第2個站的平均等待時間的預測準確率分別為98.40%和98.14%，對串聯排隊系統的平均等待時間的預測較優．

4 機器學習與近似方法的比較

目前，對于到達過程為更新過程，服務時間服從一般分布的排隊系統的平均等待時間的研究均采用近似方法． 文獻[24]研究了GI/G/1排隊系統的平均等待時間． 文獻[6]基于文獻[24]的方法使用排隊網絡分析方法(QNA)研究了具有非馬爾可夫性的串聯排隊系統的平均等待時間． 基于布朗運動，文獻[7]利用一階矩和二階矩的近似方法提出了使用QNET方法估計串聯排隊系統中顧客的平均逗留時間．

為了驗證本文方法的有效性，下面分別對GI/G/1-G/1系統以及M/G/1-G/1系統的平均等待時間的誤差進行比較．

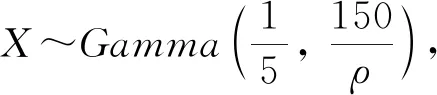
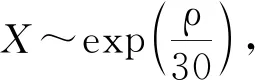
對于上述串聯排隊系統，分別采用Kingman方法以及本文提出的XGBoost方法對第1個站的平均等待時間進行預測；使用QNA，QNET以及本文提出的XGBoost方法對第2個站的平均等待時間進行預測，各種方法預測的相對誤差如表4，5所示．

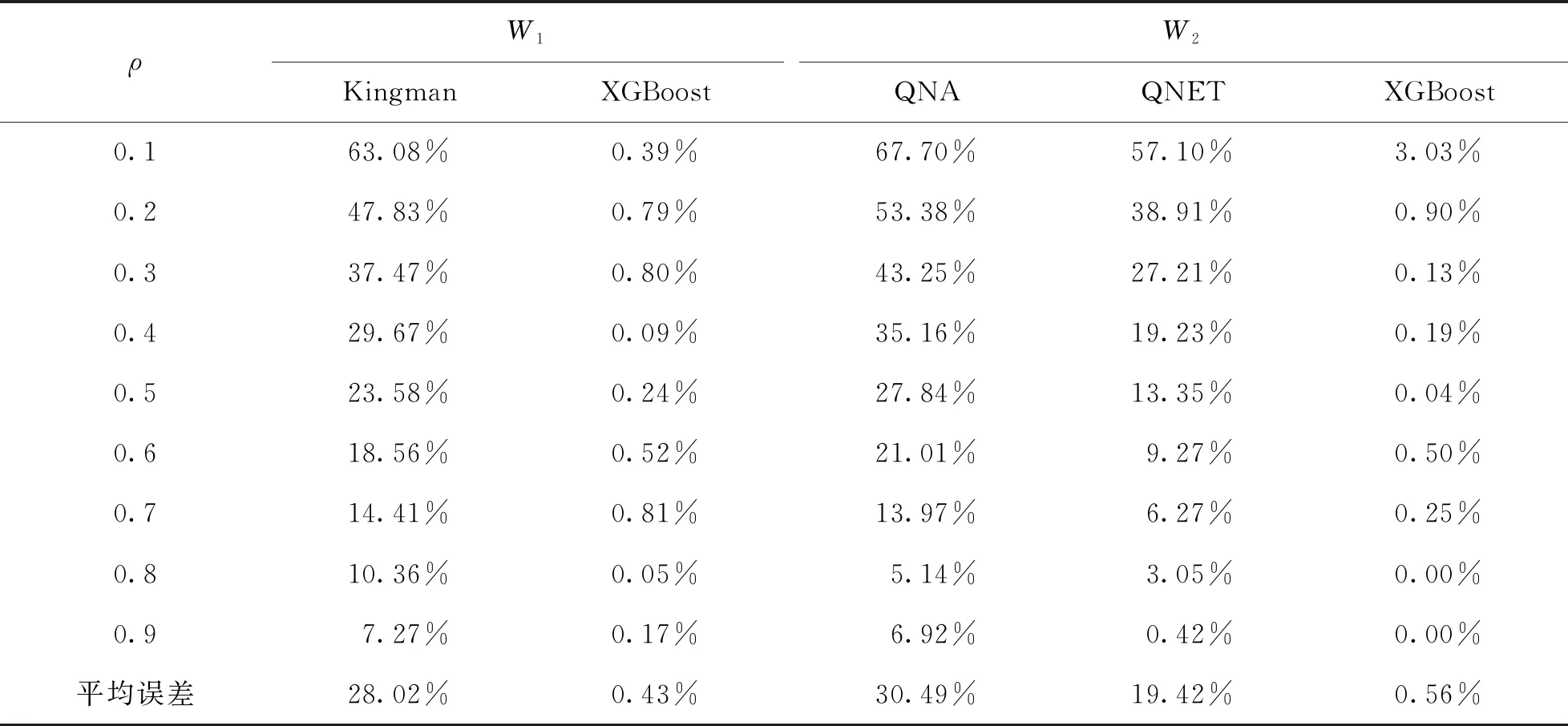
表4 系統1中兩個站的平均等待時間的相對誤差比較

由表4可知，在不同的繁忙程度下，對于第1個站的平均等待時間，XGBoost方法、 Kingman方法的平均相對誤差分別為0.43%，28.02%． Kingman方法是對平均等待時間上限的近似分析，其預測效果比XGBoost方法差．

對于第2個站的平均排隊時間，XGBoost方法、 QNA方法以及QNET方法的平均相對誤差分別為0.56%，30.49%以及19.42%． 相比于其他方法，XGBoost方法的相對誤差最小且平均誤差均小于1%． 在繁忙程度ρ較小時，顧客的平均等待時間較短，相對誤差較大． 由此可知，本文提出的XGBoost方法明顯優于其他方法，并且在繁忙程度ρ較大時，預測效果最佳．

在M/G/1-G/1排隊系統中，第1個站的平均等待時間存在精確解析表達式，因此，僅對第2個站的平均等待時間的相對誤差進行比較． QNA方法、 QNET方法均通過考慮離去過程的一階矩和二階矩來刻畫串聯排隊系統中第1個站對第2個站的影響． 雖然這些方法很容易計算平均等待時間的近似值，但是其計算的精確度不高． 由表5可知，當ρ={0.1，0.2，0.3，0.5，0.6，0.8，0.9}時，本文提出的XGBoost方法相對誤差最小，XGBoost方法、 QNA以及QNET方法的平均相對誤差分別為0.83%，4.58%以及3.55%． XGBoost方法的平均相對誤差最小，QNET方法優于QNA方法，這是由于QNA方法在平方變異系數較大的情況下，參數分解方法的性能下降導致預測效果不佳[7]． 綜上所述，XGBoost方法優于其他方法，近似效果較好，能夠比較準確地計算串聯排隊系統的平均等待時間．

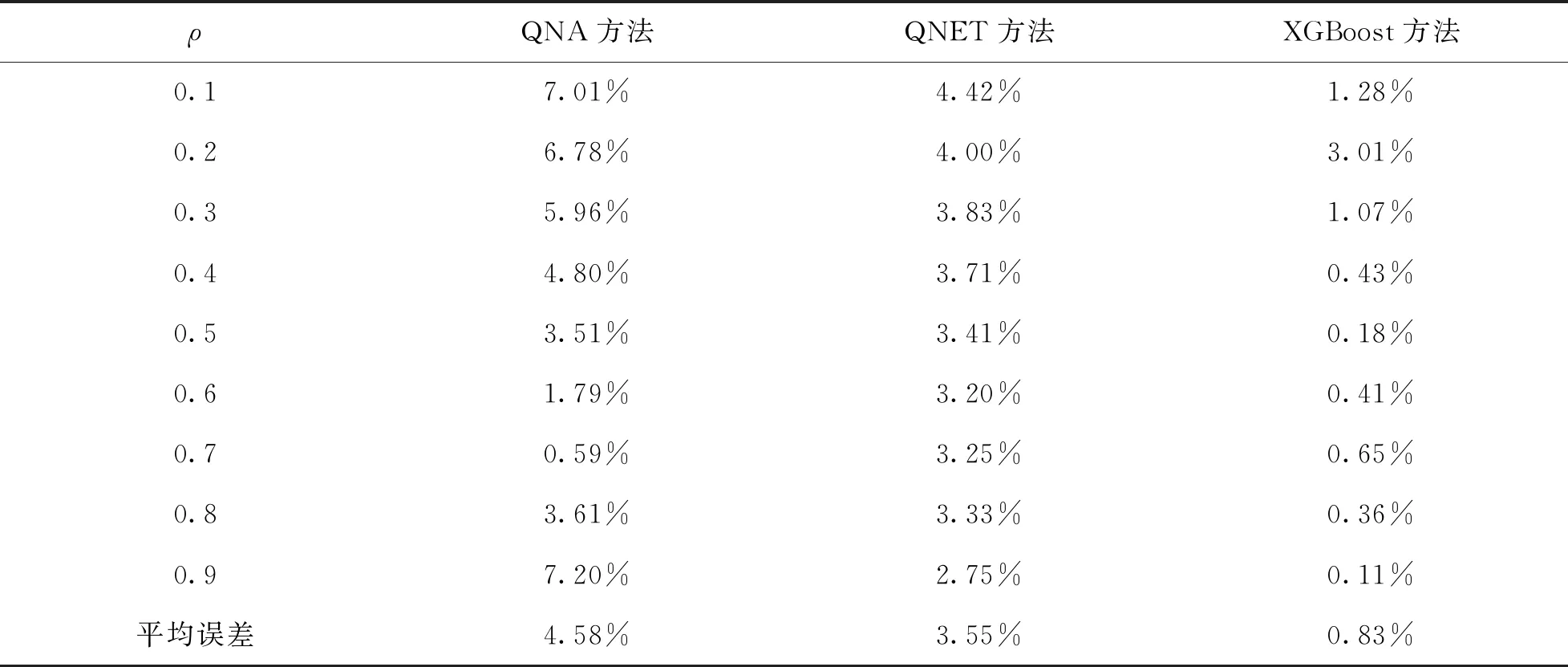
表5 系統2中第2個站的平均等待時間的相對誤差比較

5 結論

本文采用機器學習中的線性回歸算法和非線性回歸算法預測串聯排隊系統的平均等待時間． 將仿真的通用性與機器學習的計算效率相結合，提高了平均等待時間預測的準確性． 大量的數值實驗表明，XGBoost方法對平均等待時間的預測效果較好．

本文主要研究了兩個站的串聯排隊系統，未來可以使用該方法對其他排隊系統進行深入研究，例如具有多個服務站的串聯排隊系統、 具有有限緩沖區的串聯排隊系統、 具有批量服務的串聯排隊系統以及復雜的排隊網絡等．