訪問多個特定相對位置的航天器軌道設計

夏存言，張 剛，耿云海，周斯騰

(1.哈爾濱工業大學航天學院衛星技術研究所，哈爾濱 150080；2.哈爾濱工業大學航天學院，哈爾濱 150001)

0 引 言

隨著航天事業的發展，航天任務的多樣性和復雜度都日漸增加。在眾多的航天任務中，航天器軌道設計和軌道確定問題對于任務規劃、在軌跟蹤等環節都是十分重要的研究內容。同時，隨著航天器的低成本化和小型化，越來越多的航天任務不再是由單獨的一個航天器來完成，而是多航天器共同實現任務目標。此類任務中，航天器之間往往是近距離飛行，其相互狀態往往比其自身在慣性空間內的飛行狀態更加受到關注[1]。

在航天器相對運動的眾多相關問題研究中，訪問特定的空間相對位置對于很多航天任務均有重要的應用價值。當追蹤航天器的軌道周期與目標航天器的軌道周期不同時，其相對運動軌跡在空間中是一條非閉合曲線，經過特定相對位置的軌跡可以用于確定空間非合作目標的運動狀態[2]，近距離太空碎片清除[3]等任務。當軌道周期一致時，兩航天器滿足伴飛條件，可以實現長期的特定點重訪任務，經過特定相對位置的軌跡對于航天器在軌服務[4]、空間攻防對抗[5]等任務有著重要意義。對于要求經過多個給定目標位置的軌道設計或確定問題，雖然在考慮慣性系下的航天器絕對運動軌跡時，有如給定兩目標點與飛行時間的Lambert方法[6]、給定三共面目標點的Gibbs三矢量定軌方法[7]等經典方法，但是對于相對運動下的此類問題，由于坐標系是旋轉坐標系，所以給定的空間相對位置在慣性系下不是固定不變的，并不能夠通過絕對軌道的相關理論得到訪問特定相對位置的相對運動軌跡，因此，對于相對運動空間中的三矢量定軌方法的研究，在航天器在軌服務、空間攻防對抗等任務中，對目標航天器從特定方位(特定相對距離及特定方向)上進行偵查等任務中具有重要意義。

另一方面，由于空間相對距離往往較近，相對速度較小，所以相對運動的動力學及運動學模型在對問題的研究中比慣性空間的絕對軌道動力學模型更具優勢。在航天器相對運動問題研究中，線性相對運動模型因其可以得到解析形式的狀態轉移矩陣而得到廣泛研究與應用。針對目標航天器為圓軌道和橢圓軌道，基于相對位置和速度的經典Clohessy-Wilyshire(CW)方程[8]和Tschauner-Hempel(TH)方程[9]分別被提出和完善改進。同時，基于相對軌道根數的相對運動模型也以其更便于表示航天器間的軌道關系得到了充分發展[10]。線性化的相對運動模型相比于非線性動力學模型，雖然在精度上會產生些許誤差，但解析解的存在為進一步研究復雜的相對運動問題提供了有利的條件,例如近距離交會對接任務[11]、航天器編隊飛行任務[12]等。

線性模型的狀態轉移矩陣[13]可以提供經過兩個空間相對位置的相對軌道設計算法。但是當給定三個相對位置或加以伴飛約束條件時，問題的求解復雜度也會隨之提升。對于訪問空間中多個相對目標點的伴飛軌道設計問題求解，目前仍少有相關的理論方法，Bai等[14]首次通過相對軌道根數模型將問題轉化為求解七維非線性方程組的問題，并對其進行了細致的后續維持策略研究，為此類問題的研究提供了新的思路。但其對于非伴飛情況沒有進行考慮。同時，方程組的維度過高，會提升迭代過程收斂的難度。而以相對軌道根數模型對問題進行分析，對于航天器相對位置速度狀態的體現也不足夠直觀。

基于以上有關介紹，本文以相對位置速度的直觀狀態量入手，將慣性空間中的三矢量定軌方法拓展到相對運動空間中。基于CW與TH方程，對包括圓軌道、橢圓軌道以及共面、異面在內的情況進行綜合分析，給出各種情況下的約束方程與自變量的個數，并且將各種情況下的特定相對位置訪問問題均簡化為一維或二維非線性方程組問題，同時給出簡潔的迭代初值選取策略;提出一種比較簡潔有效的空間特定相對位置訪問方法。

1 坐標系介紹與問題描述

1.1 坐標系及坐標轉換

本文共應用到兩種參考坐標系，分別為地心慣性坐標系(ECI)及目標軌道坐標系(TOC)。ECI坐標系選為國際常用的J2000坐標系；目標軌道坐標系原點位于目標航天器質心，Z軸指向地球質心，X軸在軌道平面內垂直于Z軸且指向軌道速度方向，Y軸構成右手直角坐標系(指向軌道角動量的反方向)，如圖1所示。

由ECI向TOC轉換的坐標轉換矩陣可以表示為以下形式：

(1)

式中：s*=sin(*),c*=cos(*);i,Ω分別為S0的軌道傾角和升交點赤經；u=ω+f為緯度幅角，ω,f分別為近地點幅角和真近點角。

需要注意的是，由于TOC系是一個旋轉坐標系，在進行速度轉換時，需要對其進行考慮。位置和速度的轉換關系式應分別寫為：

(2)

1.2 相對運動的狀態轉移矩陣

在相對運動的問題研究中，針對主星圓形軌道的CW方程以及橢圓主星軌道的TH方程都是線性化的常用方程。二者都可以寫成狀態轉移矩陣的形式，避免了數值積分，為相對運動相關問題的研究提供了十分便捷的基礎條件。本文的后續分析求解等工作也均基于CW或TH方程進行，此處對二者的狀態轉移矩陣形式做簡要介紹。

首先，相對運動狀態轉移矩陣的一般化形式可以寫為：

(3)

對于式(3)中的各分項Φ，當S0軌道的偏心率e0≠0時，即為TH方程的狀態轉移矩陣，其表達形式在文獻[13]及[15]中有著詳細的描述與介紹。而當e0=0時，則可化簡為CW方程的狀態轉移矩陣，表達形式如下：

(4)

1.3 問題描述與分析

訪問給定相對位置條件下的軌道確定問題可以描述為：求解跟隨航天器S1的軌道參數，使其能夠在t1,t2和t3時刻分別經過給定的兩個或三個相對目標位置R1,R2和R3。特別地，周期性重訪約束條件是指S1的軌道周期與S0的軌道周期一致，使其能夠周期性經過給定的相對目標位置。

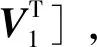
同時，約束方程的數量從問題描述中即可確定。假設S1在t1時刻以R1的相對位置出發，其需要滿足的約束方程為

(5)

因此，約束方程的數量在異面條件時為6，共面條件時則為4。

通過上述分析可以發現，本文的研究問題可以分為以下四種情況：

(1)e0=0,S0與S1軌道共面：約束方程數量為4，待求解參數數量為4；

(2)e0=0,S0與S1軌道異面：約束方程數量為6，待求解參數數量為5；

(3)e0≠0,S0與S1軌道共面：約束方程數量為4，待求解參數數量為5；

(4)e0≠0,S0與S1軌道異面：約束方程數量為6，待求解參數數量為6。

所以，對于情況(1)和(4)，其約束方程數量與待求解參數數量相同，可以直接對問題進行分析求解研究；對于情況(2)和(3)，待求解參數的數量分別少于、多于約束方程的數量，使得相應問題不存在一般解或具有無窮多解，則可以通過調整改變約束條件使其約束與變量個數一致。本文中，重點考慮的額外約束條件為周期性重訪約束。對情況(2)，減少一個目標相對位置，同時增加周期性重訪約束；對情況(3)，額外增加周期性重訪約束，則二者的約束方程數量與待求解參數數量均為5，可進行相應分析求解。

結合以上分析，本文將對以下四種情況分別進行訪問給定相對位置條件下的軌道確定問題求解：

(a)e0=0,S0與S1軌道共面，過三個目標相對位置；

(b)e0=0,S0與S1軌道異面，過兩個目標相對位置，周期性重訪；

(c)e0≠0,S0與S1軌道共面，過三個目標相對位置，周期性重訪；

(d)e0≠0,S0與S1軌道異面，過三個目標相對位置。

2 問題求解

2.1 情況(a)：共面圓軌道過三目標

當e0=0,S0與S1共面時，由式(3)和(4)可以寫出訪問三個給定目標相對位置的4個約束方程：

(6)

通過對方程組中的①②④式進行消元處理，省略中間過程，可以得到Δt3關于Δt2的解析表達式：

(7)

式中：

其中：

將式(7)代入式(6)中的③式，即可得到只關于時間Δt2的一元一維非線性方程，記為

F(Δt2)=0

(8)

其中涉及到的V1z和V1x表達式為：

(9)

(10)

可以通過分段黃金分割+割線法等常用的一維數值搜索算法快速求其在自變量約束范圍內的所有可行解。

需要說明的是，由于本文研究中使用的是線性相對運動模型，得到的結果在真實的飛行環境下由于空間中的各種攝動力的作用，會存在位置誤差(短時間內誤差量級較小，具體情況將在第3節仿真算例中給出)。但這種誤差都可以通過后續的微分修正過程進行修正，本文的方法仍然可以用于快速設計標稱軌道。

2.2 情況(b)：異面圓軌道周期重訪二目標

當目標相對位置包含面外量時，根據1.3節的分析，首先將目標位置數量減少至2個，同時增加周期性重訪約束，此時問題的約束方程可以寫為：

(11)

不難發現，當只需經過R1和R2時，由式(11)中的上式可以直接將相對速度V1寫成關于時間Δt2的函數形式：

(12)

也就是說，任意的飛行時間Δt2都可以確定S1在相對位置R1處的相對速度V1，因此，只需要求解Δt2使得其對應的V1能夠滿足a1=a0即可。所以，需要建立起S1軌道的半長軸a1關于其在相對位置R1處的相對速度V1的函數關系。

由式(2)可以得到在t1時刻，S1在ECI系下的位置和速度矢量為

(13)

同時，由活力公式可知

(14)

結合式(13)及(14)，即可得到a1關于其V1的函數關系：

(15)

G(Δt2)=a1-a0=0

(16)

同樣可以通過一維數值搜索算法在給定的時間約束范圍內求解。

2.3 情況(c)：共面橢圓軌道周期重訪三目標

當S0的軌道為橢圓軌道時，狀態轉移矩陣需采用TH方程的形式[15]。根據2.3節情況(c)可以建立問題的約束方程組為式(17)～(19)。

(17)

(18)

a1=a0

(19)

式(17)和(18)中的Φ,R,V均只考慮XZ平面內分量。同時V1可以表示為下面兩種形式

(20)

對方程組作消去V1處理，可以將約束方程組重新寫為式(21)及(19)的形式。

V1,t1t2-V1,t1t3=0

(21)

此時方程組維度為3，待求解參數為t1,t2及t3。對于維度大于1的非線性方程組，通常采用Newton迭代的方法對其進行求解，但是需要給出合理的迭代初值以保證收斂性。如果采用離散化網格點搜索算法，理論上，方程組的維度每增加一維，初值搜索的計算量都將巨量增加。所以，如何快速提供迭代初值是解決此問題的關鍵。

注意到雖然約束條件有所不同，但是S1軌道的半長軸a1的表達形式是一致的，均可以由式(15)表示。與情況(b)不同的是，由于e0≠0,a1不再只是關于Δt2的一元函數，而是關于t1和t2(或t3)的二元函數，而這取決于V1的表示方式選擇為式(20)中的上式或下式。分別記兩種a1的表示方法為如下形式

(22)

則當t1給定任意值時，對應滿足周期性重訪約束的t2和t3可以分別通過H1及H2以一維數值搜索方法確定。這一結果可以直接降低方程組的迭代維度。基于該結果，方程組可降維并重新寫為：

(23)

對式(23)進行一維數值搜索求解，即可得到該情況下問題的解。

2.4 情況(d)：異面橢圓軌道過三目標

對于情況(d)，也是最具有一般性的情況，其約束方程可以表示為如式(17)和(18)的形式。

此時，Φ,R,V既包含面內量，也包含面外量。同樣對方程組進行消元運算，消去V1，方程組即可重新寫為如式(21)一樣的形式。

不同的是，此時這是一個三維的非線性方程組，同樣很難直接搜索得到迭代求解的初值點。所以，仍然需要通過一定的方法對方程組進行降維簡化處理。注意到在相對運動的方程中，XZ平面內的運動與Y軸上面外的運動是互相解耦的。也就是說，此時該問題的方程組可以分別寫為二維的XZ面內運動方程組和一維的面外運動方程。面內的二維方程組的形式與情況(c)完全相同，此處主要對面外的一維運動方程進行分析。Y軸方向軌道面外的運動方程記為

(24)

式中：根據文獻[15]有

(25)

將式(25)代入式(24)，整理后可得：

(1+ecf2)sf3-f1R2y-(1+ecf3)sf2-f1R3y-(1+

ecf1)sf3-f2R1y=0

(26)

由軌道方程可知

(27)

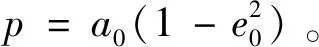
(28)

不難看出，在式(28)中，f1～f3,r1～r3都分別為t1～t3的函數，同時，r2又可以寫作f2的顯式函數。所以，將式中與f2相關的項提取出來，整合后可得：

Pcf2+Qsf2+E=0

(29)

式中：

(30)

通過三角函數關系求解方程，可得

(31)

式中：

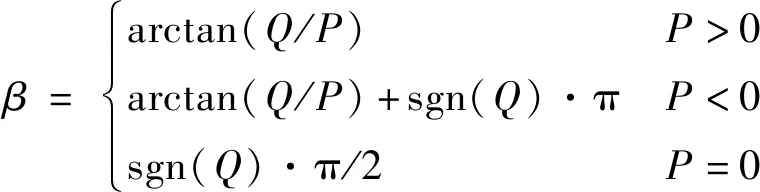
(32)

求解得到f2以后，時刻t2則可以通過求解Kepler方程獲得。

在中國，椰子的種植面積相對于其他作物還是較少的，更多的人考慮到研究成果的市場問題之后都選擇了放棄。所以，對于這種地域性較強的科研項目，國家要加大政策和資金扶持力度，發揮政府在組織創新方面的鼓勵、支持、引導和協調的重要作用，為合作組織帶動型的發展創造良好的外部環境，這也能為中國海南建設國際旅游島提供動力 。

通過上述過程，我們將方程組中的面外方程轉化為了一個t2關于t1和t3的表達式。這樣，方程組可以被簡化為只包含t1,t3的二元二維方程組。這對于迭代求解的初值選取工作是十分有利的。對于二元二維的非線性方程組，其迭代初值可以通過網格法[16]輕松獲取。設計指標函數如下式：

U(t1,t3)=‖V1,t1t2-V1,t1t3‖

(33)

式(33)中的Φ,R,V均只考慮XZ平面內的分量。

利用網格法將t1和t3進行網格化，計算U的值，進行網格法搜索。選擇U值較小的網格點作為初值，進行Newton迭代求解方程組，即可得到區間內的解集。

2.5 J2攝動模型下的解

2.5.1微分修正法

通過前文的理論過程，已經可以得到二體引力模型下該系列問題的解，但考慮到實際太空飛行環境中還包含有各種攝動力的影響，且以地球非球形引力攝動的J2項影響尤為明顯。二體引力模型的假設以及基于線性相對運動模型得到的解在真實物理環境下會有相應的位置訪問誤差，因此，為了提高方法的實用性，還需要對J2攝動模型下的相應問題進行求解。本文采用微分修正法[16]求解此問題。

微分修正的基本步驟可以描述如下：

步驟1：確定待修正參數向量x，以及誤差向量Er；

步驟2：通過數值差分算法，求取誤差向量Er關于待修正量x的Jacobian矩陣J；

步驟3：通過如下迭代公式，對x進行修正，直至誤差大小滿足給定的指標。

xm+1=xm-J-1Er,m=1,2,…

(34)

式中：m為迭代次數。當m=1時，x1作為迭代初值，即為二體模型下的解。

2.5.2修正參數的確定

具體的，對于前文分析的四種情況，進行微分修正時，自由變量x及誤差向量Er分別如下：

情況(a)：

(35)

式中：δR2x,δR2z,δR3x,δR3z分別表示在t2,t3時刻對R2,R3的面內X，Z方向上的位置訪問誤差。此時x與Er均為四維。情況(a)中對于t1的選擇是任意的，考慮J2攝動時，仍然可以任意給定t1，因為在共面、不需要周期重訪的條件下，J2攝動對軌道的影響程度較小。

情況(b)：

(36)

情況(c)：

(37)

情況(d):

(38)

式中：δR2,δR3分別表示t2,t3時刻，S1對目標相對位置R2和R3的三軸訪問誤差。此時x與Er均為六維。對于不含有周期重訪約束條件的情況，可以直接對三軸訪問位置誤差進行修正。

通過以上過程，分別將二體模型下得到的結果作為初值在J2攝動模型下進行迭代修正，就可以得到相應的J2攝動模型下的解。下面給出各種情況的仿真算例。

3 仿真算例

在仿真中，首先需要給出各種情況下的S0的軌道參數，以及對應情況下S1所需要訪問的特定目標點的相對位置。相關參數見表1。

S0軌道的其他參數在各情況下均為

[a0,i0,Ω0,ω0,ft0]=[12000 km,30°,60°,45°,0°]

(39)

下面分別對四種情況給出算例。

3.1 情況(a)：共面圓軌道過三目標

由2.1節的理論分析過程可知，在該情況下，Δt3可以表示為Δt2的顯式函數，問題轉化為一元一維非線性方程。但需要注意的是在求解反三角函數時，在[0,2π]區間內存在兩個解，要注意分別考慮。

給定時間約束范圍為Δt2∈(0,2T],Δt3∈(0,2T]。T為S0的軌道周期。在給定的時間約束范圍內，通過分段黃金分割+割線法對方程在時間區間內進行一維數值求解，得到該問題的解集。同時，由于圓軌道條件下t1時刻不會對相對運動情況產生影響，因此對于情況(a)和情況(b)，均選取t1為初始時刻，即t1=0。

表1 S0軌道偏心率、需訪問目標點及周期性重訪約束初始條件Table 1 Orbital eccentricity of S0,positions to be visited and periodic revisit constraints

此外，將S1在訪問R2和R3時所飛行的“圈數”分別為N2和N3，記為：

(40)

最終可以得到問題的解集，進一步以二體線性模型下的解為初值進行微分修正，可以得到與二體線性模型解逐一對應的J2攝動模型下的解，解集可見表2中的情況(a)。

用數值積分的方式，分別繪制二體模型下的解和修正得到的非線性J2攝動模型下的解在非線性J2攝動力學模型下的相對運動軌跡圖，結果如圖2所示。圖中Pi(i=1,2,3)表示矢量Ri(i=1,2,3)在空間中的位置。可以看出在非線性J2攝動力學模型下，基于二體線性模型得到的結果也可以保證較高的訪問精度，經計算，其對于R2,R3的訪問誤差分別為[0.049,5.968] m。而當經過修正后，對應的J2下的1號解則可以實現更為精確的訪問，即使修正過程沒有對Y軸的面外方向進行考慮，訪問誤差也均可被降低至10-2m量級。

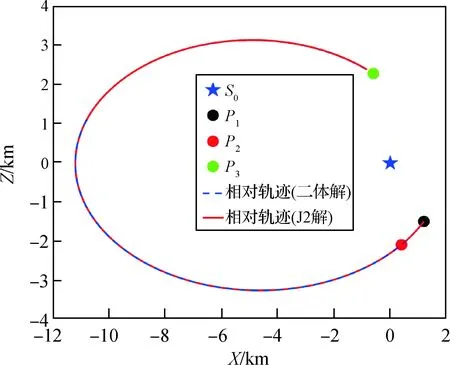
圖2 情況(a)相對運動軌跡Fig.2 Relative motion trajectories of Case (a)

3.2 情況(b)：異面圓軌道周期重訪二目標

由2.2節的分析可知，情況(b)的相關約束最終可化簡為式(16)的關于Δt2的一元一維非線性方程。考慮到周期重訪的約束條件，只需在Δt2∈(0,T]的時間約束范圍內，通過分段黃金分割+割線法即可快速求解即可。將得到的解進行微分修正，得到J2攝動模型下的解，結果記錄如表2中的情況(b)所示。

表2 J2攝動條件下各情況解集Table 2 Solutions of each case under J2 perturbation condition

將二者分別在J2攝動模型下積分得到的相對運動軌跡圖如圖3所示，考慮到周期重訪約束，飛行軌跡的時間區間設置為[t1,t1+5T]。

經計算，二體線性模型的解在5個軌道周期中，對R1,R2的訪問誤差分別從[0,0.069] m逐漸擴大至[220.436,228.684] m。而經過修正后的J2模型的解，相應的訪問誤差則從第一周期的精確訪問緩慢擴大至第五周期的[109.531,100.327] m。可以看出J2模型下的解可以有效地降低周期訪問誤差。此外，還可以看出在該組仿真算例的條件下，二體線性模型得到的解與J2模型下的解較為接近，因此該組二體線性模型的解對R1,R2的周期訪問誤差較小，但仍可看出經過修正后的結果周期訪問效果明顯更佳。

3.3 情況(c)：共面橢圓軌道周期重訪三目標

在該情況下，考慮周期性重訪約束，t2和t3可以分別表示為t1的函數[式(22)]。從而通過t1可以直接求得J(t1)的值。考慮有周期性重訪約束，給定時間約束范圍為t1∈[0,T],t2∈(t1,t1+T],t3∈(t1,t1+T]。

在t1∈[0,T]的范圍內，在時間范圍約束內，求解J(t1)=0，得到可行解集，并通過微分修正，得到J2攝動模型下的解集如表2情況(c)所示。

繪制二體解與J2解在[t1,t1+5T]時間區間內，在非線性J2攝動力學模型下積分得到的相對運動軌跡如圖4所示。可以看出二體線性模型下的解在J2攝動模型下，相對運動軌跡會隨著時間產生漂移，從而導致位置訪問誤差逐漸增大，在5個軌道周期內，對R1,R2,R3的訪問誤差分別從[0,0.302,322] m快速擴大至[2391,2439,2026] m。但經過修正得到的J2模型下的解相較之下則可以保證更高的訪問精度。經計算，修正后的解在5個周期內的相應位置訪問誤差分別從[0,0.172,3.005] m緩慢擴大至[114.280,131.392,36.193] m。可以看出經過修正后的解，能夠有效地降低周期訪問位置誤差，保證一定的周期重訪精度，對于近距離偵查觀測等任務具有相應的應用價值。

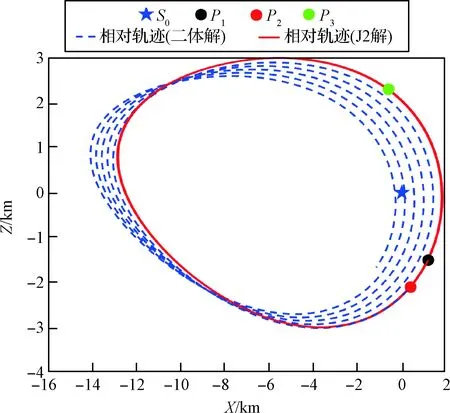
圖4 情況(c)1號解相對運動軌跡Fig.4 Relative motiontrajectories of Case (c),solution No.1

3.4 情況(d)：異面橢圓軌道過三目標

由2.4節的分析可知，t2可以通過面外方程表示為t1,t3的顯式函數，從而使三維非線性方程組降至二維，通過網格法搜索t1,t3的迭代初值。同樣地，由于求解t2時需要進行反三角函數的運算，在搜索初值時也應對反余弦函數的符號正負分別考慮。由于情況(d)中不包含周期性重訪約束條件，所以我們將飛行時間約束放寬至2T，即t1∈[0,T],t2∈(t1,t1+2T],t3∈(t1,t1+2T]。通過設定U的取值上界，篩選出較為合理的初值點。

為了更好地表示解的存在空間，以t1∈[0,T],t2∈(t1,t1+T]的時間區間，且式(32)的反三角函數取正號為例，以U<0.3 m/s為篩選條件，給出初值搜索的等高線圖如圖5所示，其他相應區間的搜索方法和結果均相同。

圖5 初值搜索等高線圖Fig.5 Contour map for searching initial values

將篩選出的初值點進行Newton迭代求解。借助于網格法搜索結果，從解的分布情況上著手，最終在時間約束范圍內的可能存在解的區間內，求得相應的可行解，并通過修正過程，得到J2攝動模型下的可行解集合如表2情況(d)所示。

繪制二者在J2攝動模型下的相對運動軌跡如圖6所示。可以看出在較短時間內，二體線性模型的解可以保持較高的訪問精度。經計算，二體線性模型的解對R2,R3的位置訪問誤差分別為[93.464,29.065] m。而經過修正后，由于對三軸方向均進行了修正，因而可以實現精確位置訪問。

圖6 情況(d)1號解相對運動軌跡Fig.6 Relative motion trajectories of Case (d),solution No.1

4 結 論

對于訪問多個特定相對位置的航天器軌道確定問題，按照目標航天器的軌道形狀為圓或橢圓，以及目標航天器和追隨航天器的軌道是否共面分為四種情況進行求解。其中，軌道異面，且目標航天器為圓軌道情況時，可以經過兩個特定相對位置，并實現周期性重訪。對于其他三種情況，均可以實現相對運動模型下的三矢量定軌。并且，共面且目標航天器為橢圓軌道的情況還可以實現周期性重訪的三矢量定軌。通過理論分析推導，使每種情況下的問題最終都簡化為求解一或二維非線性方程(組)的問題，并提出了有效的求解策略。并進一步基于二體線性模型得到的結果，通過微分修正策略，對不同的情況分別在J2攝動的力學模型中進行修正，并得到相應的J2攝動條件下的結果。

經過仿真分析，可以發現該問題的解并不唯一，存在多解現象。同時，本來采用線性相對運動方程得到的解，在飛行時間較短的情況下，在J2攝動模型中仍然具有較高的訪問精度，但是當考慮周期重訪條件，或飛行時間較長時，J2引力攝動對于訪問精度會產生較大的影響。而通過微分修正方法，可以有效地降低其影響，提高訪問精度。本文提出的方法可以有效地用于訪問多個特定空間相對位置的航天器軌道設計。