也談高中數學形式化及其教學

段志貴，張 雯

也談高中數學形式化及其教學

段志貴1，張 雯2

（1．鹽城師范學院 數學與統計學院，江蘇 鹽城 224000；2．南京師范大學 教師教育學院，江蘇 南京 210023）

有關數學形式化及其教學曾在20世紀90年代引發廣泛討論．伴隨著中國高中數學課程標準從2003年實驗版到2017年版及其2020年的重新修訂，革新教學內容、改革教學方式成為時代發展的必然要求，重新認識和探討新時代數學形式化及其教學具有十分重要的意義．基于文獻研究和思辨性分析，提出數學形式化即是數學內容的抽象化與數學概念的符號化．數學形式化具有過程性、層次性及關聯性等特點．與科學數學相比，學科數學重在傳承、生長和理解，其形式化有所淡化．新的高中數學課程標準有關形式化內容表述的修訂并非舍棄形式化的學習要求，而是力求更客觀、更具體，體現適度性．改進高中數學形式化內容的教學要遵循“注重過程，漸進導入”的教學原則，運用情境化引入，降低形式化門檻；漸進性鋪墊，搭建形式化平臺；符號化呈現，揭示形式化內涵；鞏固性訓練，促進形式化理解．

高中數學；數學形式化；教學策略；注重過程；漸進導入

1 問題提出

自20世紀90年代以來，中國數學教育界對于是否需要“淡化概念”，怎樣處理數學教學中的“實質”與“形式”，有過比較廣泛的討論[1]．陳重穆、宋乃慶兩位數學教育界前輩針對數學教育脫離教學實際的現象提出要基于學生年齡特點“淡化形式，注重實質”[2–3]．但也有人認為，為適應信息社會對數學發展以及相關學習內容下移的要求，要逐步加強數學的形式化教學[4–5]．更多學者提出在數學教學中要正確處理好數學形式化與非形式化之間的關系，兩者不可偏廢[6–7]．研究者曾就這一話題，與部分高中數學教師交流，讓人詫異的是不少教師對有關數學形式化教學并不關注，部分教師甚至根本不知道數學形式化的內涵，錯把數學形式化理解為一般意義上的一種教學方式．基于走訪調查和文獻分析，研究發現當前高中數學教師在數學形式化教學上的困惑主要包括“什么是數學形式化”，“數學形式化具有哪些特點”，“新課程標準下的高中數學形式化教學有否具體要求”以及“怎樣組織和實施高中數學形式化教學”等．針對這些問題，立足學科核心素養培養，結合進入21世紀以來中國兩次頒布的高中數學課程標準對形式化內容的教學要求，思辨性地探討高中數學形式化教學內容及其教學方式，以期為高中數學形式化教學提供合理化建議和參考性樣例．

2 數學形式化的界定

2.1 數學形式化的內涵

數學形式化是指對數學內容進行提煉、整理、組織，使其從具體到一般，并用數學語言表達出來的過程[8–9]．概括地說，就是內容的抽象化與概念的符號化．其目的是從復雜的現實中提取出數學本質或一般規律，用符號替代冗長的表述或表達深刻的思想，以利于簡化和概括，助推認知、理解或深入研究．初等數學中的“用字母表示數”，即是一種最基本的數學形式化．形式化是數學的基本特征之一，符號化則是形式化的高級形態．

從數學研究目的上看，數學以簡潔的形式化符號（或其它數學語言）表征，揭示出現實世界的數學本質與規律；從數學研究對象上看，數學研究的是對現實世界數量關系和空間形式逐級抽象后形成的形式化思想材料；從數學研究過程上看，各個數學模塊（或分支）經過形式化的加工，都能構成一個相對完整的公理體系，例如從自然數系開始形成的代數學和從歐幾里得幾何開始形成的各種幾何學，都是形式化數學的范例．縱觀數學的演進與發展，不難發現形式化有助于數學的發現和創造，有助于數學的嚴格化、系統化和現代化．近現代數百年的數學發展歷程表明，中國數學與西方數學有著較大差距，原因之一就是西方較早創立數學符號并利用了數學的形式化．

數學形式化的形成與發展是人類智慧的結晶．千百年來，人類在適應和改造自然的生活實踐中，經歷識別、聯想、分析、推理、綜合和表征等思維過程，從中提煉數學思想、抽象數學符號并獲取各種數學意義；再回歸數學學習與研究中去，對數學符號進行不斷地改造、簡化或淬煉，以形成特定的數學形式和內涵．數學形式化的學習，使得人們對數學符號不只知道“表示什么”，更能深入地了解這些符號“意味著什么”，從而為數學符號賦予“新的意義”，讓死板、枯燥的數學因為符號的參與具有了審美意趣，賞心悅目．

2.2 數學形式化的認識和理解

數學抽象是數學最基本的思維方式[10]，形式化是其最顯著的特點之一．更全面地領會數學形式化的本質，需要正確認識并深刻理解數學形式化的過程性、層次性及其關聯性．

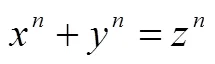
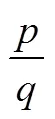
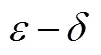
3 作為學科的數學形式化

學科，也稱科目，是依據一定的教學理論組織起來的科學基礎知識體系[11]．為了滿足數學教學需求，學科數學需要對科學數學進行內容篩選、調整并根據不同學段重新編排，力求切合各學段學生的年齡特點和身心發展規律[12]．

3.1 學科數學形式化與科學數學的比較

學科數學與科學數學，一個是數學的教育形態，一個是數學的學術形態，二者既有聯系又有區別．學科數學是在合乎教學要求的基礎上，對科學數學內容的取舍，它既包括了科學數學上有定論的、比較穩定的、重要的基礎知識，如概念、原理、規律和基本事實等[13]，又涵蓋了對數學文化和數學價值（應用、思維等）的描述．與科學數學相比，學科數學的形式化有所弱化，主要緣于以下3個方面．

一方面，學科數學重在傳承，具有教書育人取向的社會性．科學數學活動的任務是探索、發現人類未知的數學規律，完善和發展數學的科學體系，解決數學理論與應用的前沿問題．而學科數學的任務則是使學生獲得進一步學習以及未來發展所必需的“四基”“四能”，能夠會用數學的眼光觀察現實世界，會用數學的思維思考現實世界，會用數學的語言表達現實世界．

另一方面，學科數學重在生長，遵循學生認知發展的規律性．科學數學的特點是高度的抽象性、嚴密的邏輯性、廣泛的應用性．作為學科的數學，雖然也具有上述特點，但其抽象性、嚴謹性的程度卻沒有科學數學那么高，也不必那么高，它處于一種合理的“中間狀態”．因而，著眼于學生身心發展水平和認知規律，采用相對具體、直觀的教學方式可能更有利于學生的學習理解和能力培養．

再一方面，學科數學重在理解，強調知識發生發展的過程性．對于科學數學而言，其工具性特點和高度簡約化特征必然要求其從現實中剝離出來，概括、抽象并高度凝練，以達到一般化，實現形式化．排斥形式化即是限制科學數學本身的發展．歷史上，拒絕萊布尼茲發明的微積分符號曾使得英國數學落后歐洲數學數十年．而對于學科數學，則一般是從生活情境入手，從人類認識的初始狀態介入，通過暴露數學知識的發生發展過程，讓學生從中積累數學活動經驗，獲得數學思想方法的體驗或感悟，以利于不斷提高思維層次和認識水平[14]．

3.2 學科數學形式化的課標要求

2003年教育部頒布的《普通高中數學課程標準（實驗）》（以下簡稱“實驗版”）[15]對“數學形式化”明確提出要“強調本質，注意適度形式化．”“形式化是數學的基本特征之一．在數學教學中，學習形式化的表達是一項基本要求，但是不能只限于形式化的表達，要強調對數學本質的認識．”值得關注的是，《普通高中數學課程標準（2017年版2020年修訂）》（以下簡稱“2020修訂版”）[16]刪除了這一表述．統計兩版課標中出現的“形式”與“形式化”的次數及其文本呈現例證，如表1所示，不難發現，“2020修訂版”中對“數學形式化”的描述大篇幅減少，但是有關“形式”與“數學形式”的表述并沒有減少，在此顯示出較強的靈活性，讓實際教學具有了一定的彈性空間．

此外，研究也關注到與形式化密切相關的“語言”及其聯結詞，包括“自然語言”“生活語言”“圖形語言”“符號語言”“數學語言”以及具體的“代數語言”“集合語言”“向量語言”等，在“實驗版”中出現了78次，在“2020修訂版”中出現了82次；專門論述有關“自然語言”“圖形語言”“符號語言”之間遞進關系的論述，“實驗版”和“2020修訂版”出現的次數一樣多，都是5次．

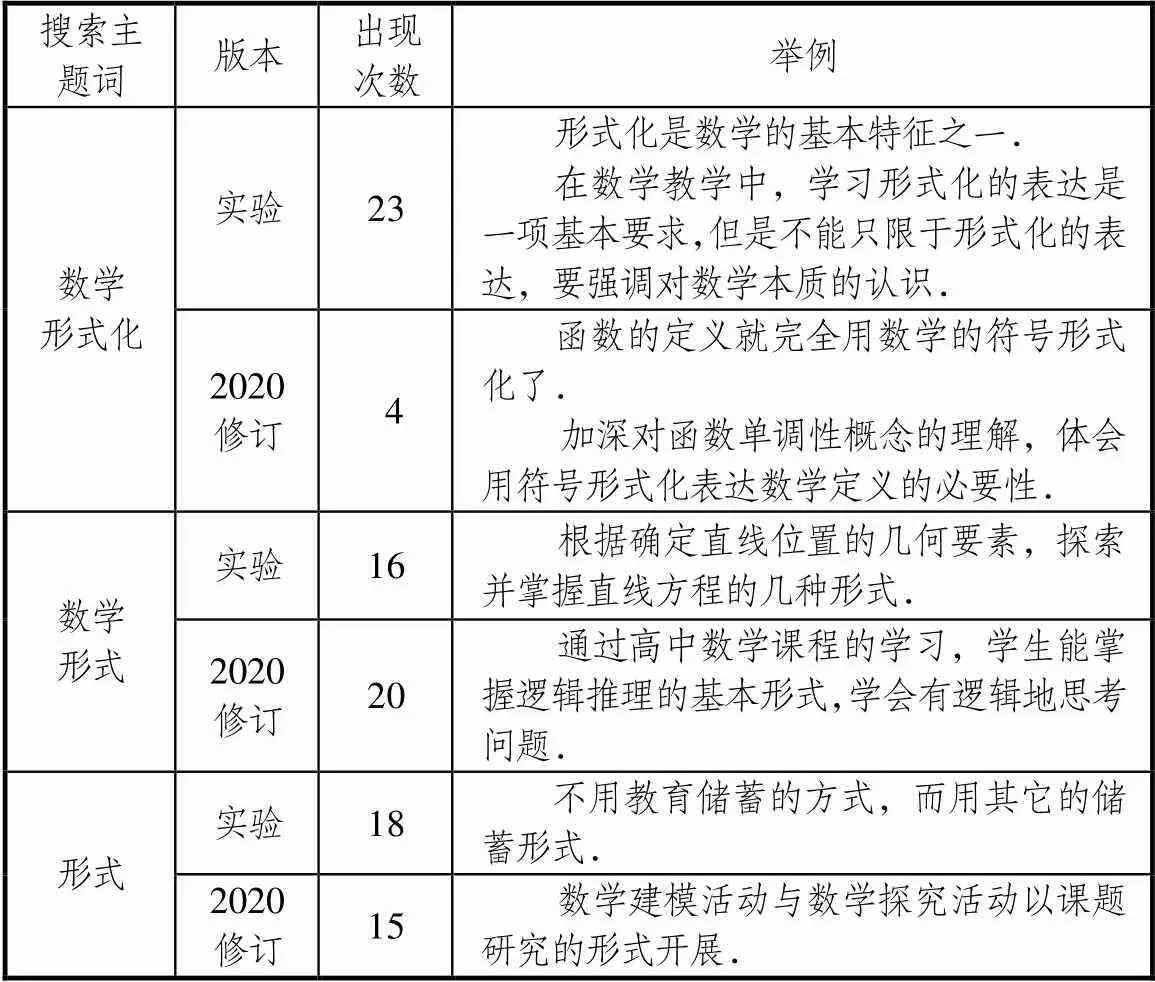
表1 課標中的“形式”與“形式化”的統計

由此可見，“2020修訂版”課程標準中對形式化內容表述的修訂并非舍棄形式化的學習要求，而是力求更客觀地服務于數學學科核心素養的培養，更具體地貼近學生學習和學科教學的需要，對形式化既不片面拔高，也不無端忽視．概言之，高中階段的形式化不一定是完全意義上的形式化，帶有一定的相對性．正確認識、理解和執行課程標準，就要明確高中數學形式化只能是向著數學形式化過渡的數學語言，或是幫助理解具有數學學科特點的表達形式．這些數學語言或表達形式都是形式化教學的基本內容和呈現方式，合乎培養學生“數學抽象”素養的教學要求．

3.3 學科數學形式化教學的“度”

數學教材是高中數學教學的重要工具，也是學生知識的重要來源．但數學教材上的知識（定義、演繹、推理等）一般只是呈現形式化的結果，有血有肉的探索性發現過程有可能被省略了．教師若照本宣科，則學生只是按照“記憶—應用”的被動模式學習，就會掩蓋數學的思維過程，忽略數學本質的揭示．

20世紀60年代西方推行的高中數學課程改革，即所謂的“新數學運動”，過分強調結構化、抽象化和形式化，片面追求演繹推理，忽視歸納、類比推理，遠遠超過了中學生的平均能力和身心成熟程度，最終以失敗告終．試想在高中“弧度制”內容的教學中，如果教師僅僅告訴學生，“1弧度的概念是弧長與半徑相等時所對應的圓心角”，“弧度制是利用半徑與弧長的比衡量角的新單位”，學生就可能既不清楚弧度制產生的必要性，也難以理解弧度的概念，更談不上靈活運用了．有調查發現一部分學生在有關角的運算問題上，仍然下意識地采用角度制進行計算，思維受限，效率低下，正是這個原因所造成的．

顯然數學學習的過度形式化是不可取的，然而摒棄數學學習內容的形式化也是不科學的，繁雜冗長的敘述同樣不是數學應有的表現形式．實踐證明，高中數學適度形式化，不但有助于數學信息的記憶和使用，而且也能幫助學生加深對所學數學知識的認識和理解．試想如果教師對教學內容理解的不到位，降低或放棄形式化內容的學習要求，只教學生聯系實際或直觀看圖去理解、記憶概念，套用公式和題海戰術去掌握技能，長此以往怎么能有效地激發學生數學思考，構建有效的數學能力結構？這樣教出來的學生往往缺少數學形式化的“澆灌”和“打磨”，開放性思維極可能受阻，遇到不曾見過的問題必然束手無策，后續進階學習也可能因此障礙重重，更談不上創新發展了．

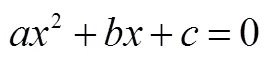
4 高中數學適度形式化教學策略

基于數學形式化的特點，結合高中數學課程標準兩個版本的共性要求，提出高中數學形式化及其教學既不能簡單舍棄，也不能急速冒進，要遵循“注重過程，漸進導入”的教學原則．一方面，要精心創設生動形象的問題情境展示教學內容的發生發展過程，揭示數學形式化表征與數學本質的內在聯系；另一方面，要依據學生的認知特點，低起點、有坡度，漸進鋪墊，適時凝練，引領學生逐步建立抽象的數學形式化結構．

遵循上述原則，在具體內容的教學上，以“函數的單調性”一課為例，結合學情需要，把教學過程分解為“情境化引入、漸進性鋪墊、符號化呈現、鞏固性訓練”等4個階段，簡稱為“引—墊—現—練”4個階段，如圖1所示．

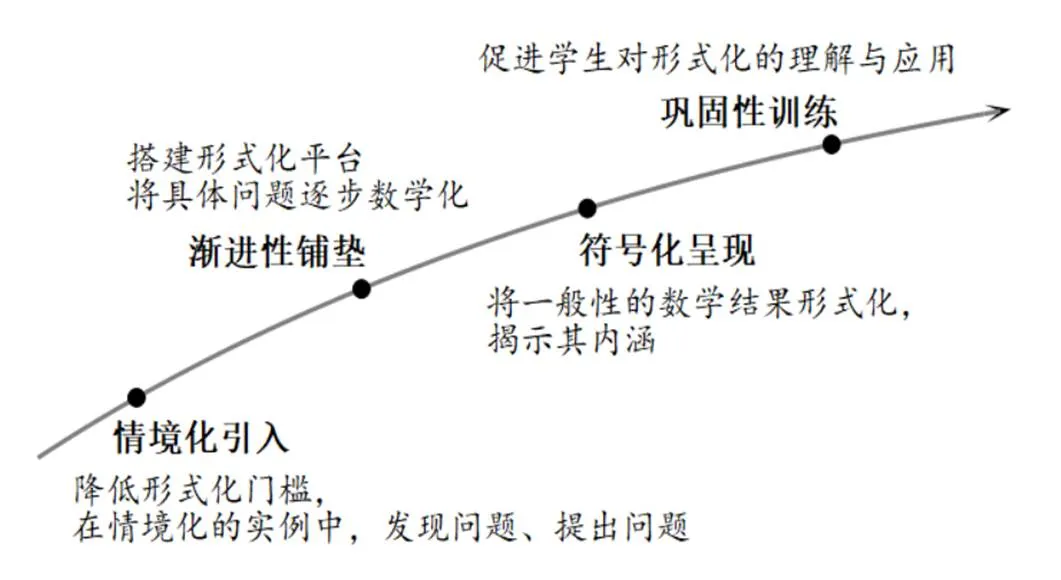
圖1 高中數學適度形式化“引—墊—現—練”教學策略

4.1 情境化引入 降低形式化門檻

正如荷蘭數學教育家弗賴登塔爾所說，“學生對于數學的認識始于常識．”[19]他們對數學表達的認識和理解總是從日常的、非正式的推理開始．高中數學形式化的課堂教學首先應精選或創設與數學知識密切相關、符合學生實際，并且含有一定思維水平的情境引入問題．有關情境及其問題既不能脫離該節課學習的主題，也不能過于簡單．前者只是象征性地走過場，還有可能會使部分學生產生誤解，后者則不能調動學生思維，對發展學生的核心素養價值不大．這些情境和問題應能將數學與現實的關聯性、漸次生長的抽象性形象化地揭示出來．只有這樣，才能讓學生在具體的、可操作的活動中發現問題、提出問題，逐步提升抽象化思維水平．

天氣預報和氣溫變化圖是學生日常生活中比較熟悉的，并且也與函數單調性有著密切的聯系．在“函數的單調性”教學的第一階段，不妨以當地某天的氣溫變化圖為實例創設情境．可以先讓學生仔細觀察氣溫隨時間的變化圖（如圖2所示），利用“氣溫變化的規律是什么？”“這一天什么時間段內，氣溫在上升？什么時間段內氣溫在下降？”等問題啟發學生思考，讓他們通過對給定一天氣溫變化的觀察，先直觀、具體地感受單調性，以形成對“單調遞增”“單調遞減”的初步理解．接著，進一步提問“如果從數學的角度看，這些規律又是什么呢？”“能用數學語言描述嗎？”聚焦學生思維，引出課題——函數的單調性．這樣既能激發學生的求知欲，使其帶著問題聽課，也能讓學生感受到數學來源于生活，服務于生活．

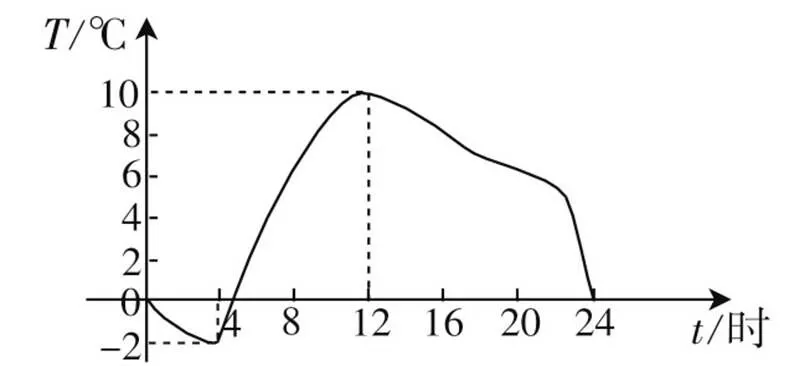
圖2 某地某天氣溫變化

情境化的引入使得比較抽象的數學形式化內容有了具體化“臺階”．這些富有啟發性的問題情境，助力學生拾階而上，在對有關情境問題的思考或作答過程中，不知不覺進入到數學學習之中，突破抽象化的桎梏，為后續形式化內容的學習奠定基礎．

4.2 漸進性鋪墊 搭建形式化平臺

情境化與形式化都十分重要，但二者并不一定直接相連．從情境化逐步形式化的過程應是“非正式—預形式—形式化”．一般說來，預形式是對情境化前提的一種數學化解讀，常常在小組討論和合作交流中發生發展．顯然預形式具有漸進性鋪墊功能，為形式化概念的建立搭建了平臺．

教學中的鋪墊，不能簡單地理解為學生小組討論，而是要在學生已經了解具體問題的基礎上，引導學生確定其中蘊含的數學成分及其關系、規則，厘清或架構各成分之間可能存在的內在關系，并嘗試運用數學語言表達出來．簡言之，就是將現實的或熟悉的情境性問題逐步數學化，促進學生產生由具體到抽象的認知圖式．從方式方法上看，教學中的漸進性鋪墊離不開師生之間的互動交流．有的教師在教學過程中缺少這樣的鋪墊，總是迫不及待地想教給學生形式化的符號，這樣做欲速則不達，反而會使得一部分學生產生表達與理解上的困難，以致望而生畏，止步不前．

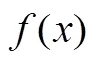
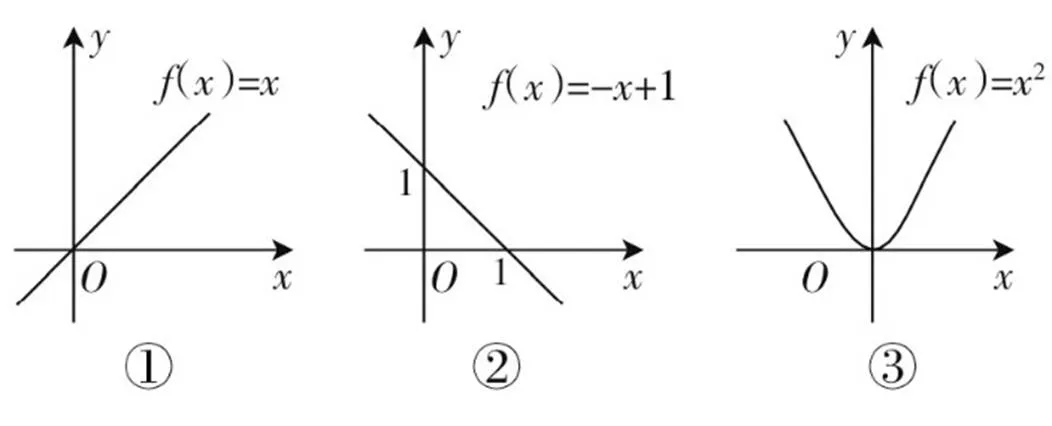
圖3 3個初等函數圖象

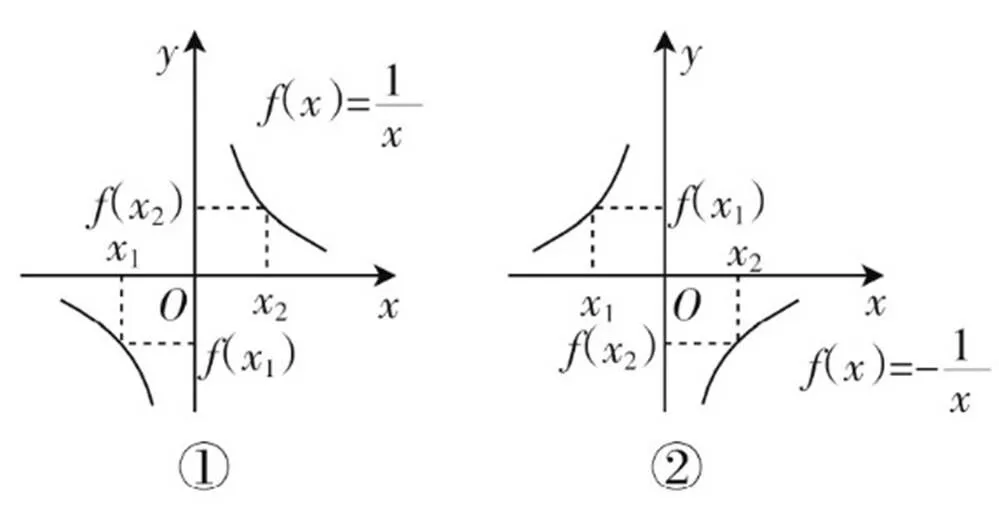
圖4 反比例函數圖象

漸進性鋪墊有助于學生數學思維的逐步提高，有助于他們數學建模等能力的逐步發展，學生在與教師、其他同學的互動交流中，能夠逐步理解概念的本質，完善精確概念的表達，也能從中建立起概念本質與數學形式化之間的聯系，把那些碎片化、非正式的數學理解過渡到結構化、形式化的數學表征上來[20]．

4.3 符號化呈現 揭示形式化內涵

美國著名數學教育家詹姆斯·希伯特和托馬斯·卡朋特合作建構的“表示—聯系”理解框架[21]，明確提出學生對于數學概念意義的理解來自兩方面：一是數學符號與其它表示形式之間的聯系；二是數學符號語言內部的聯系．對形式化數學結果的理解與記憶是高中課堂教學最基本的目標，因此，高中數學課堂教學應在學生對相關情境性問題思考的基礎上，注重數學知識的整體性與結構化，關注不同數學知識之間的聯結，促進學生形成特定內容模塊的知識網絡．

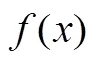
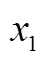
4.4 鞏固性訓練 促進形式化理解

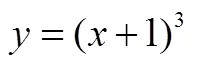
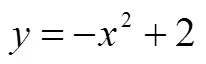
值得注意的是，有關數學形式化的教學并非一節課就能徹底完成．事實上，人們對數學形式化的認識是分階段，逐步遞進和加深的[22]．因此，一節課內容往往只是形式化內容的初步建立，也許還不夠完善，還需要在后續學習中進一步充實，使之內涵更豐富，運用更便捷，表達更清晰．就函數單調性形式化表達的建立來說，除了在高一年級第一學期“函數的概念與性質”這一模塊教學中出現，在其它時間、其它內容的學習上還可能經常遇見，即人們常說的“螺旋式上升”．為此，在后續有關單調性相關內容的教學上，教師可以通過適切的設問誘思及其鞏固性訓練，幫助學生夯實理解基礎，提升抽象思維水平和符號化表達能力，為不斷進階的函數性質及其應用的學習建構通道．

正如宋乃慶、陳重穆所說的那樣：“淡化（形式）是相對的，不是不重視，更不是取消形式．”數學形式化是數學學習不可或缺的重要內容，也是數學教學，特別是高中數學教學的重要組成部分．遵循“注重過程，漸進導入”的數學教學原則，相信高中數學形式化內容及其教學決不是跨不過去的坎、趟不過去的河．只要在日常教學中能夠結合學生特點，準確把握課標要求，“引—墊—現—練”，因材施教，就一定能把冰冷美麗的數學形式化內容轉變為學生火熱的思考，助推學生在積極主動的數學學習過程中提升關鍵能力，發展核心素養．

[1] 羅靜，王光明．數學教學中形式化與非形式化的研究綜述[J]．中學數學教學參考，2008（5）：49-50，59．

[2] 陳重穆，宋乃慶．淡化形式，注重實質——兼論《九年義務教育全日制初級中學數學教學大綱》[J]．數學教育學報，1993，2（2）：4-9．

[3] 宋乃慶，陳重穆．再談“淡化形式，注重實質”[J]．數學教育學報，1996，5（2）：15-18．

[4] 數學教育研究小組．數學素質教育的熱點透視[J]．數學教學，1994（2）：2-4．

[5] 方厚良，羅燦．學習形式化的表達是數學教學的一項基本要求[J]．中學數學，2015（9）：57-59．

[6] 王光明，張文貴．數學教學中有關形式與非形式的幾個問題[J]．數學教師，1997（10）：4-8．

[7] 鄭毓信．再談“淡化形式，注重實質”——《淡化形式，注重實質》讀后[J]．數學通報，1994，33（8）：6-7．

[8] 王躍紅．數學形式化及其存在問題[J]．數學通報，2006，45（3）：16-19．

[9] 張敏，何小亞．數學教學原則的反思與重構[J]．中學數學研究（華南師范大學版），2017（19）：1-5，53．

[10] 李昌官．數學抽象及其教學[J]．數學教育學報，2017，26（4）：61-64．

[11] 中國大百科全書出版社編輯部．中國大百科全書·教育[M]．北京：中國大百科全書出版社，1985：5-6．

[12] 喻平，董林偉，郭慶松．中學生數學品格與價值觀的問卷設計[J]．數學教育學報，2021，30（4）：12-18．

[13] 蘇帆．關于學科數學與科學數學[J]．數學教育學報，2007，16（1）：34-36．

[14] 路江江，王亞妮．高中數學教育中如何培養學生的數學核心素養——王尚志教授訪談錄[J]．數學教育學報，2021，30（2）：67-70．

[15] 中華人民共和國教育部．普通高中數學課程標準（實驗）[M]．北京：人民教育出版社，2003：2–11．

[16] 中華人民共和國教育部．普通高中數學課程標準（2017年版2020年修訂）[M]．北京：人民教育出版社，2020：5-8．

[17] 張奠宙，王振輝．關于數學的學術形態和教育形態——談“火熱的思考”與“冰冷的美麗”[J]．數學教育學報，2002，11（2）：1-4．

[18] 羅展華．高中數學教學中形式化與非形式化的表現特征[J]．中學教研（數學），2009（4）：12-14．

[19] 趙曉燕．荷蘭現實數學教育的教學設計原則——逐步形式化[J]．數學通報，2012，51（8）：20-24．

[20] 王欽敏，余明芳．數學思維素養深度涵育：教學的進路與方略[J]．數學教育學報，2020，29（6）：56-60．

[21] MULLIS I V S, MARTIN M O, SMITH T A, et al. TIMSS assessment frameworks and specifications 2003 [M]. 2nd ed. US: International Study Center, Lynch School of Education, Boston College, 2003: 9-34.

[22] 馬淑杰，張景斌．高中學生數學原有知識水平和學習認知負荷對數學課堂學習效率的影響研究[J]．數學教育學報，2021，30（2）：26-31．

Also on High School Mathematics Formalization and Its Teaching

DUAN Zhi-gui1, ZHANG Wen2

(1. School of Mathematics and Statistics, Yancheng Normal College, Jiangsu Yancheng 224000, China;2. School of Teacher Education, Nanjing Normal University, Jiangsu Nanjing 210023, China)

The formalization of mathematics and its teaching have aroused extensive discussion in the 1990s. With the revision of the mathematics curriculum standard of senior high school in China from the experimental version in 2003 to 2017 and its revision in 2020, the innovation of teaching contents and teaching methods has become the inevitable requirement of the development of the times. It is of great significance to re-understand and explore the formalization of mathematics and its teaching in the new era. Based on literature research and speculative analysis, it is proposed that mathematical formalization is the abstraction of mathematical content and the symbolization of mathematical concepts. Mathematical formalization has the characteristics of process, hierarchy and relevance. Compared with scientific mathematics, subject mathematics focuses on inheritance, growth and understanding, and its formalization has been diluted. The revision of the formal content expression of the new mathematics curriculum standard in senior high school is not to abandon the formal learning requirements, but to strive to be more objective, more specific, and appropriate. To improve the teaching of formal content of mathematics in senior high school, we should follow the teaching principle of “paying attention to process and gradual introduction”, using situational introduction to lower the formal threshold, gradually paving the way and building a formal platform, symbolizing presentation to reveal formal connotation, and strengthening training to promote formal understanding.

high school mathematics; mathematical formalization; teaching strategies; process-oriented; progressive introduction

G632

A

1004–9894（2022）06–0060–05

段志貴，張雯．也談高中數學形式化及其教學[J]．數學教育學報，2022，31（6）：60-64．

2022–07–11

江蘇高校哲學社會科學重點課題——《鄉村教師支持計劃（2015—2020）》下的鄉村教師身份認同與專業成長研究（2017ZDIXM151）；江蘇省教育科學“十三五”規劃課題——數學學慢生“慢學習”的實踐研究（B-b/2020/02/217）；鹽城師范學院教育教學改革重點課題——師范類專業認證背景下的數學教學論課程教學改革的探索和思考（2018YCTUJGZ011）

段志貴（1966—），男，江蘇鹽城人，教授，碩士生導師，主要從事數學課程與教學論研究．

[責任編校：周學智、陳雋]