鋼化真空玻璃在溫差作用下的變形特征

高 帥，岳高偉，藺海曉，李敏敏，劉 慧

(河南理工大學土木工程學院，焦作 454000)

0 引 言

真空玻璃作為新一代節能環保玻璃，具有其他種類玻璃無法比擬的隔熱、隔聲等優越性能，但是由普通玻璃制成的真空玻璃因強度低等問題制約了其應用和發展[1]。而將普通玻璃經過加熱—淬冷處理后得到的鋼化玻璃，其表面形成的壓應力層極大地提高了承載能力[2]。與普通玻璃相比，同等厚度的鋼化玻璃抗彎強度是普通玻璃的3～4倍,抗沖擊強度更是普通玻璃的3～5倍，同時具備破碎后的碎片小、無尖銳鋒角等安全性能[3]。此外，鋼化玻璃本身強度較大，可以適當地增大支撐物間距，對真空玻璃的隔熱性能和視覺效果起到優化作用[4-5]。

在應用過程中發現，鋼化真空玻璃兩側存在溫差時易發生彎曲變形，甚至出現密封開裂使鋼化真空玻璃漏氣(失效)的現象。造成這種現象產生的原因主要有兩種：(1)鋼化真空玻璃導熱性極低；(2)溫度較高側玻璃發生線膨脹。真空玻璃具有極低的導熱性，董慧敏[6]、李宏等[7]采用試驗測試和數值模擬的方法，分析了不同類型玻璃的導熱系數，結果表明真空玻璃導熱系數遠小于其他類型玻璃，滿足節能環保的要求。Hu等[8]、趙驍真等[9]通過對支撐物參數和邊緣密封部分參數的灰色關聯評價，得到了各個指標對玻璃傳熱系數的影響程度。Zhu等[10]分析了基材玻璃的厚度、密封邊的寬度、支撐柱陣列間距以及隔熱框架結構對真空玻璃傳熱的影響。Rodriguez-Ake等[11]模擬三層玻璃窗的共軛傳熱，通過與雙層和單層玻璃對比，得出了不同真空層和玻璃基片厚度對玻璃窗抗熱性能影響。Wang等[12]利用思維進化神經網絡對真空玻璃隔熱層傳熱系數進行建模，預測了真空玻璃的保溫隔熱性能，發現玻璃在升高溫度時發生線性膨脹，使真空玻璃封接部位破裂。Memon等[13-14]研究了低溫表面感應對真空抽取、泵孔密封和復合邊緣密封的熱性能的影響，并設計、開發了真空隔熱玻璃的新型無鉛密封材料，通過減少真空邊緣密封的寬度和涂層的輻射率，改善了真空隔熱玻璃的熱性能。劉慧[15]通過實驗和數值模擬，對鋼化真空玻璃溫差變形的影響因素和安全性進行研究。李永明等[16]通過計算內外玻璃溫差作用下真空玻璃的應力和變形，分析了影響真空玻璃破裂的因素，結果表明任意尺寸的真空玻璃均有可能會因溫差作用產生破裂，且最大拉應力分布在邊角部位。蘇行等[17]、Fang等[18]利用冷熱循環試驗驗證鋼化真空玻璃可靠度，結果表明真空玻璃在經過熱冷循環試驗后傳熱率增加10.1%，真空度下降0.6 Pa，但邊緣封接部分未發生破裂，仍滿足使用要求。

本文通過鋼化真空玻璃在不同溫差下的變形試驗和數值模擬，分析了鋼化真空玻璃兩側不同溫差情況下的變形特征，為不同尺寸鋼化真空玻璃在適用環境中的變形預測提供科學方法。

1 鋼化真空玻璃溫差變形及失效測試

鋼化真空玻璃導熱率極低，對其一側加熱，受熱面玻璃膨脹變形，未受熱面基本不受影響。封接部位對受熱一側玻璃的約束力也作用于常溫側玻璃，使其協同變形。當鋼化真空玻璃彎曲受熱變形過大時，封接部位撕裂，最終導致其漏氣失效。為了研究鋼化真空玻璃溫差變形特征的影響規律，選用不同尺寸的鋼化真空玻璃在不同溫度下進行試驗研究。

1.1 試驗設備及方法

鋼化真空玻璃溫差試驗需要的設備儀器有IPC-610H工控機、耐高溫加熱墊、測溫線、控溫線、直尺、細線等。IPC-610H工控機通過控溫線和測溫線分別連接耐高溫加熱墊和鋼化真空玻璃，實時控制并讀取鋼化真空玻璃的溫度。耐高溫加熱墊對鋼化真空玻璃的一面進行加熱，使其達到預設的溫度，并保持一段時間后再測試玻璃的變形。采用交叉測量法測量鋼化真空玻璃的變形，為減小鋼化真空玻璃溫差變形試驗的誤差，同一工況下進行多次測量。

為研究尺寸和溫差對鋼化真空玻璃變形的影響，選用長寬尺寸分別為347 mm×1 344 mm、559 mm×1 984 mm、318 mm×2 120 mm的鋼化真空玻璃(5+0.5V+5，單片鋼化玻璃厚度為5 mm，真空層厚度為0.5 mm)進行試驗。鋼化真空玻璃溫差試驗步驟如下：

(1)調整IPC-610H工控機，初始溫度設定為30 ℃，加熱時間為120 min。

(2)將加熱墊粘在鋼化真空玻璃下側，并放在水平試驗平臺上。

(3)鋼化真空玻璃下側由耐高溫加熱墊加熱(加熱溫度由溫度工控機控制)，分別加熱至70 ℃、80 ℃、90 ℃、100 ℃、110 ℃，使鋼化真空玻璃兩側溫差達到40 ℃、50 ℃、60℃、70 ℃、80 ℃。

(4)設定溫度達到穩定后，在玻璃對角拉線，用直尺測量兩條對角線交叉點O到玻璃的垂直距離h，即玻璃中心變形量，鋼化真空玻璃的高溫變形示意圖如圖1(a)所示。

圖1 鋼化真空玻璃高溫變形示意圖

(5)換其他尺寸的鋼化真空玻璃重復步驟(1)～(4)，記錄數據。

1.2 試驗結果分析

鋼化真空玻璃受熱后的變形如圖1(b)所示，從圖中可明顯看出鋼化真空玻璃因受熱引起的膨脹變形。將鋼化真空玻璃溫差試驗的變形結果(玻璃中心點拱高)列于表1。

由表1可得到鋼化真空玻璃溫差變形規律：(1)同一尺寸的鋼化真空玻璃，其變形量隨溫差的增大而增大。(2)在同一溫差下，鋼化真空玻璃的變形量隨長邊尺寸增大而增大。故溫差和尺寸對鋼化真空玻璃溫差變形均有影響。

表1 鋼化真空玻璃溫差變形試驗結果

2 鋼化真空玻璃在溫差作用下的力學分析

不考慮其他約束作用，鋼化真空玻璃受溫差的變形是一個等半徑的球面。設鋼化玻璃基片厚度為η，線膨脹系數為α，支撐物高度(真空層厚度)為v，鋼化真空玻璃內外溫差為ΔT。任取彎曲球面鋼化真空玻璃的常溫面玻璃一單位長度dl為研究對象，則對應受熱面玻璃(彎曲角度)的長度為dl+αΔTdl。設常溫側玻璃中性面距球心距離為R(球面的曲率半徑)，則受熱側玻璃中性面距球心距離為R+η+v，溫度作用下鋼化真空玻璃變形協調如圖2所示。

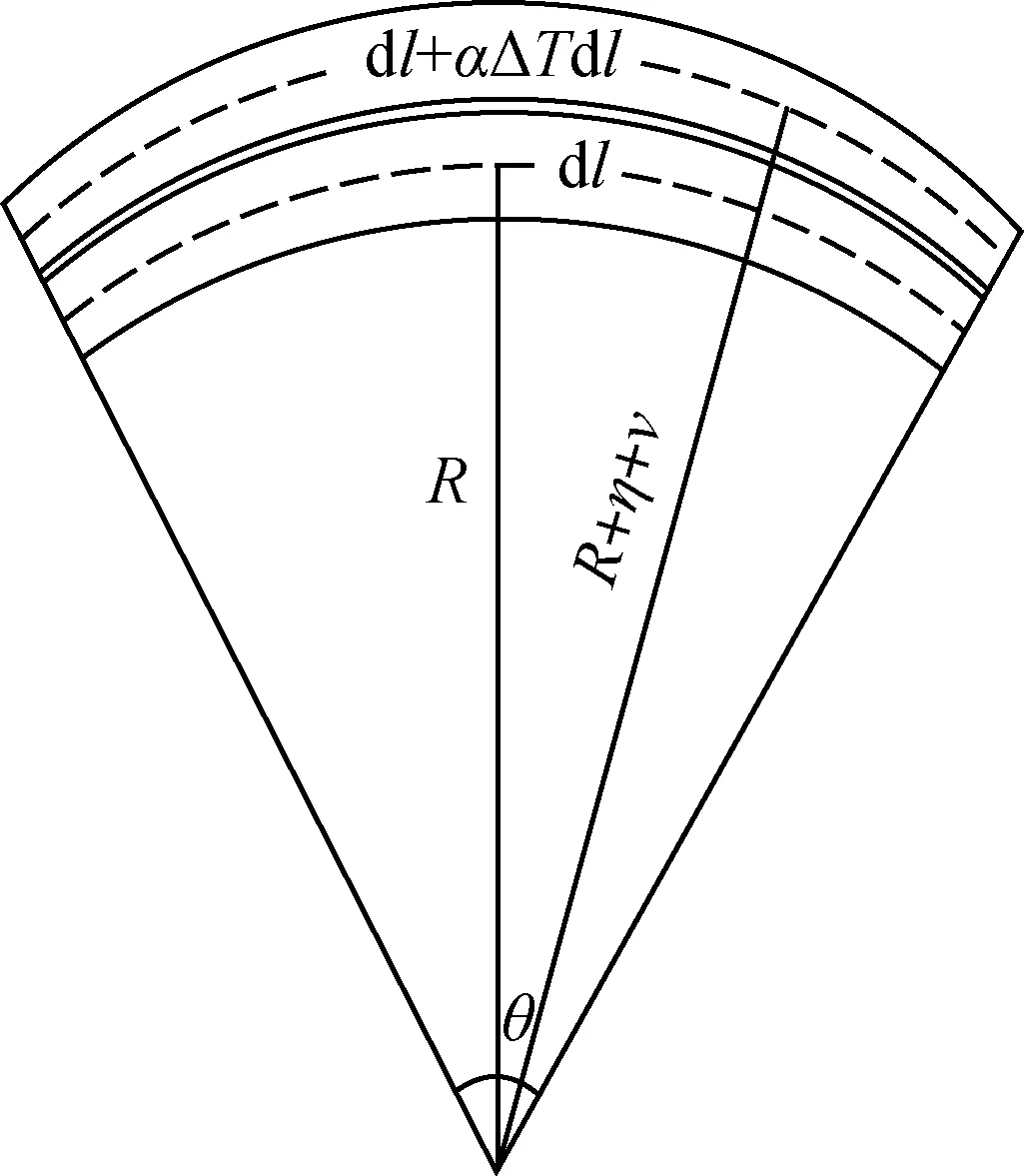
圖2 溫差作用下鋼化真空玻璃變形協調

根據變形協調關系，同時考慮玻璃板的泊松效應，溫差下鋼化真空玻璃在任一方向單位長度的變形協調滿足關系如式(1)所示。

(1)

式(1)可以簡化為

(2)

式中：μ為鋼化玻璃基材的泊松比。

由式(2)可看出，鋼化真空玻璃的彎曲曲率半徑與玻璃基片厚度成正比，與基片的線膨脹系數及兩側溫差成反比。曲率半徑越小，說明鋼化真空玻璃彎曲程度越大，對鋼化真空玻璃造成的危害越大。

3 鋼化真空玻璃溫差變形的熱-變形力學模型

鋼化真空玻璃溫差變形試驗可以得到溫差和尺寸對其變形的影響，但是服役中的鋼化真空玻璃尺寸不同，不能對其一一試驗得出變形結果。因此，通過建立鋼化真空玻璃數值模型，模擬鋼化真空玻璃溫差變形，通過對比試驗結果，分析鋼化真空玻璃數值模型的可靠性，進而可對任意尺寸的鋼化真空玻璃在其應用環境中溫差變形進行預測。由有限元軟件ABAQUS建立的鋼化真空玻璃模型如圖3所示。

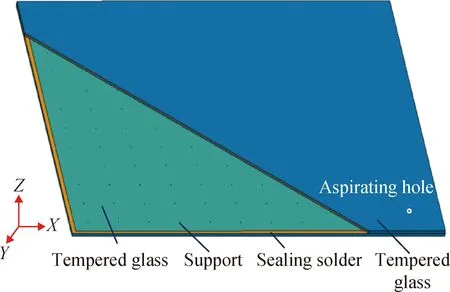
圖3 鋼化真空玻璃模型

為研究鋼化真空玻璃變形情況，對鋼化真空玻璃的簡化模型做出以下假設：(1)彈性體假設，鋼化玻璃是脆性材料，未超過極限荷載,均表現為理想彈性特性；(2)角點邊界無位移，即鋼化真空玻璃變形過程中，低溫面鋼化玻璃的四個邊角點Z軸方向位移為0；(3)連續均勻性假設，即鋼化玻璃、焊料、支撐物都是連續均勻材料。

3.1 鋼化真空玻璃模型的基本參數設定

鋼化真空玻璃由三部分組成：鋼化玻璃基片、焊料及支撐物，其中模型尺寸與試驗所用規格相同。焊料的有效寬度為0.7 mm，厚度為0.5 mm。支撐物采用Q235B不銹鋼柱，其直徑和高度均為0.5 mm。材料力學參數如表2所示。

表2 鋼化真空玻璃材料參數匯總

3.2 初始條件和邊界條件設置

為研究鋼化真空玻璃在服役狀態下的變形特征，對模型進行初始條件和邊界條件的設置。

(1)在鋼化真空玻璃上下表面施加101 kPa的大氣壓，保證其內部為真空狀態。

(2)將鋼化真空玻璃兩側初始溫度設置為30 ℃，在后續步驟中，將受熱一側鋼化玻璃溫度修改為升溫后的溫度(70～110 ℃)。

(3)將鋼化真空玻璃常溫面四個邊角點Z軸方向的位移設置為0，由此玻璃中心點位移即為鋼化真空玻璃受高溫后的最大變形量。

3.3 鋼化真空玻璃溫差變形數值模擬結果分析

根據鋼化真空玻璃溫差變形試驗中玻璃的尺寸和溫差設置，建立鋼化真空玻璃熱-變形力學模型，研究鋼化真空玻璃溫差變形規律及數值模型的可靠性。以長、寬尺寸為347 mm×1 344 mm的鋼化真空玻璃受熱變形為例說明數值模擬結果，如圖4所示。

從圖4可看出鋼化真空玻璃溫差變形具有中心對稱的特征。由于常溫玻璃面四角點的Z軸方向固定，鋼化真空玻璃溫差變形呈球面，與理論分析相符。其最大變形量在玻璃中心，向四周逐漸減小。鋼化真空玻璃溫差變形的試驗結果和數值分析結果對比分析如表3所示。

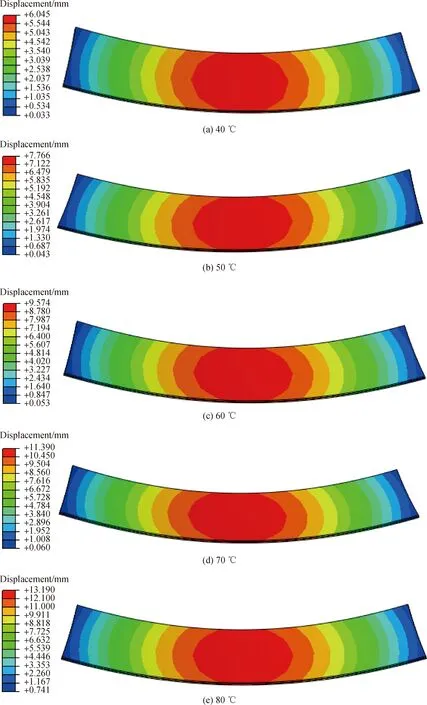
圖4 347 mm×1 344 mm鋼化真空玻璃在不同溫差下的變形數值模擬

由表3中模擬變形結果看出，鋼化真空玻璃溫差變形數值模擬的協調變形規律與試驗相吻合。即同一尺寸下的鋼化真空玻璃變形量隨溫差增大而增大；同一溫差下，鋼化真空玻璃長邊尺寸越大，變形量越大。

根據表3中誤差結果可看出，鋼化真空玻璃溫差變形數值模擬結果與實測結果基本一致，相對誤差均在5%以下，驗證了鋼化真空玻璃熱-變形力學模型是可靠的。但模擬結果與試驗結果始終存在差值，可能導致誤差的原因有以下兩個方面：

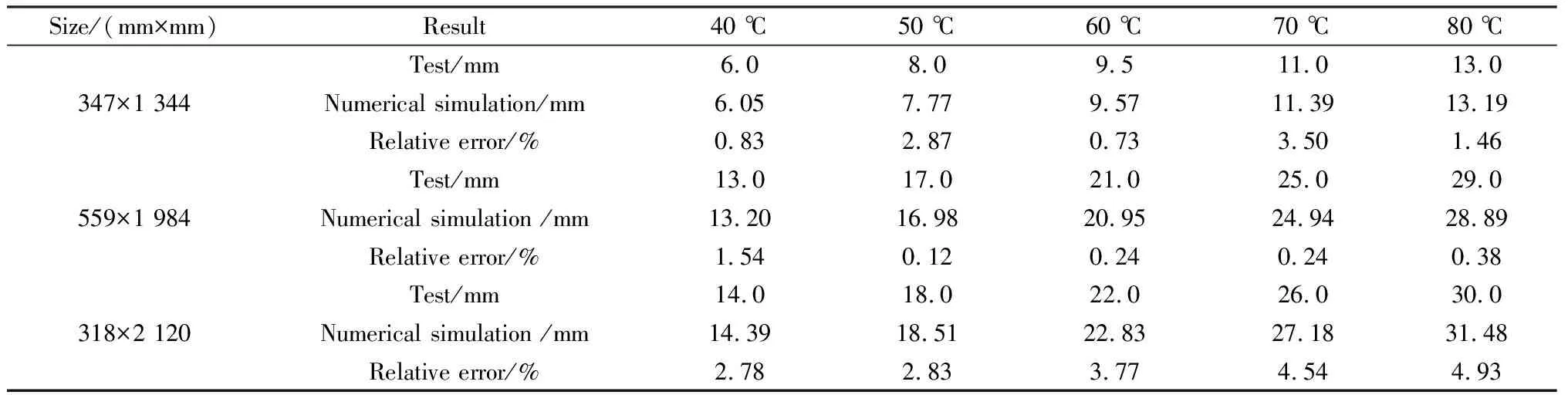
表3 鋼化真空玻璃溫差試驗和數值模擬結果

(1)試驗所使用的交叉測量法，只能減小而不能完全消除測量誤差，且受到儀器精度限制,測試結果精度有限。

(2)數值模擬所建立的鋼化真空玻璃模型是一個簡化的理想模型，模型忽略了封接焊料寬度和厚度不均勻對鋼化真空玻璃溫差變形的影響。

4 結 論

(1)鋼化真空玻璃彎曲曲率半徑與鋼化玻璃基片的厚度成正比，與基片的線膨脹系數及兩側溫差成反比。曲率半徑越小，則鋼化真空玻璃彎曲程度越大，越容易漏氣失效。

(2)鋼化真空玻璃在溫差下的變形隨兩側溫差及鋼化玻璃基片長邊尺寸的增大而增大，且長邊尺寸越大，受溫差影響的變形越明顯。

(3)數值模擬結果與溫差變形試驗結果吻合較好，說明了基于有限元軟件ABAQUS的鋼化真空玻璃熱-變形力學模型具有一定可靠性，可為各尺寸鋼化真空玻璃溫差協同變形的研究提供參考依據。