隨機粗糙面散射中遮蔽效應算法的改進

宋 哲，徐 哲，龐 勇，馬思遠，劉春楠

(遼寧師范大學 物理與電子技術學院，遼寧 大連 116029)

自然界中絕大部分物體表面都是隨機粗糙面，研究隨機粗糙面的電磁散射特性是獲取物體表面特征的關鍵途徑，在遙感領域[1]、零件檢測領域[2]、醫學領域[3]等領域有廣泛應用.隨機粗糙面散射特性的研究主要有兩種方式：數值計算和理論近似.數值計算方法主要有矩量法[4]、有限元法[5]、時域有限差分法[6]等，特點是計算量大，結果較為精確.理論近似方法主要有微擾法[7]、基爾霍夫近似法[8]等，特點是計算量小，易于理解.其中，基爾霍夫近似法計算效率高，且精度與數值計算法接近，得到廣泛應用.其核心思想是將粗糙面劃分為有限個微面元，每個微面元近似為平面，則光波在微面元上發生菲涅耳反射，由此獲得微面元上的本地場，再結合Statton-Chu積分方程得到粗糙面在空間中的散射場.

基爾霍夫近似方法的局限性在于它認為粗糙面上所有的面元都會被照射以及被散射觀測點觀測到，但事實上，當光波以一定角度入射到粗糙面上時會產生陰影區，使部分面元沒有光照射，同時，對于空間某一觀測角度也會存在部分面元的反射光因為被其他面元遮擋而無法到達觀測點，這種現象就是遮蔽效應.Beckmann首先提出了遮蔽效應的概念，并給出了單站散射的遮蔽函數表達式[9].Smith研究并給出了高斯分布下隨機粗糙表面的遮蔽概率函數[10].Wagner在Beckmann單站散射遮蔽函數的基礎上提出了雙站散射遮蔽函數[11].王安祥等人將實驗測量和遺傳模擬退火算法相結合，對雙向反射分布函數(BRDF)模型中遮蔽函數的參數進行了反演，發現反演得到的遮蔽函數參數能夠反映表面粗糙度[12].柳祎等人建立了含有遮蔽函數的偏振度模型，研究了不同粗糙度下金屬與非金屬紅外自發輻射的偏振度，發現粗糙度對非金屬表面紅外自發輻射偏振度的影響大于金屬，可用于區分金屬和非金屬[13].郭立新等人利用基爾霍夫近似給出了考慮遮蔽效應的分形粗糙表面散射截面近似公式，并討論了不同分形維數和空間基頻下遮蔽效應對雙站散射截面的影響[14].馬保科等人運用射線追蹤法研究了一維粗糙面的遮蔽效應和二次散射，計算了一維粗糙面的散射系數[15].陳明等人利用射線追蹤法研究了帶限分形粗糙面的遮蔽效應，分析了影響粗糙面遮蔽效應的因素[16].Yoshifumi等人提出一種包含多次散射的粗糙面射線追蹤(RSRT)模型，精確計算了散射分布[17].

當前遮蔽效應的研究主要有兩種方式：遮蔽概率函數和幾何遮蔽.遮蔽概率函數法是通過提出表面任意面元被遮蔽概率的函數來計算遮蔽效應的，計算量小但精確度稍差.幾何遮蔽法是通過射線追蹤，根據光線與粗糙面的位置關系來逐點判斷被遮蔽情況，計算準確但計算量大.本文將傳統的幾何遮蔽方法進行了改進，在不改變原有精確度的情況下，縮短了幾何遮蔽效應的運算時間，并在此基礎上采用基爾霍夫近似法分別計算了S波和P波入射到隨機粗糙面時的散射場分布.

1 基于Kirchhoff近似法分析隨機粗糙面的散射

呈現高斯分布的隨機粗糙面在自然界中十分常見，可用線性濾波法來構建隨機粗糙面.描述粗糙面的指標主要有相關長度l(二維粗糙面x和y方向的相關長度分別為lx，ly)和均方根高度δ，則隨機粗糙面各處的高度分布可表示為[18]

(1)

其中，M、N為x和y方向離散點的數目，Lx、Ly分別為粗糙面在x和y方向的長度，(xm,xn)為離散點坐標，當離散點的間隔為Δx和Δy時，xm=mΔx，yn=nΔy，km、kn為x和y方向的波數，km=2πm/Lx，kn=2πn/Ly，F(km,kn)為傅里葉系數，可以表示為

(2)

N(0,1)為滿足高斯分布的一組隨機生成數，S(km,kn)是二維高斯粗糙面的功率譜密度，表達式為

(3)

根據式(1)～式(3)，可分別生成M=N=500、lx=ly=3 μm、δ=0.1 μm和δ=0.3 μm的隨機粗糙面，如圖1所示.

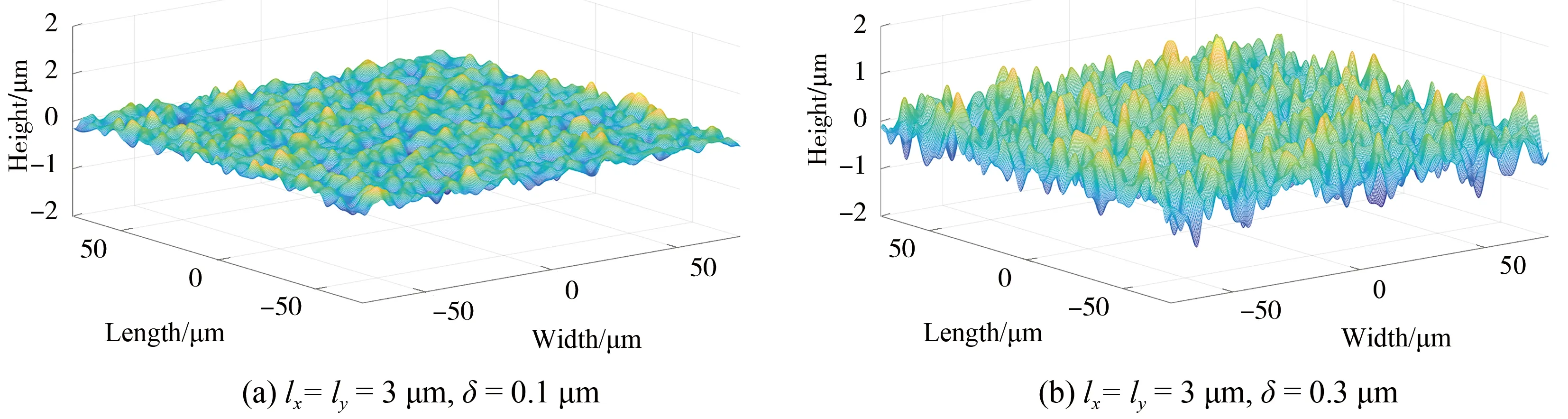
圖1 隨機粗糙面示意圖

當平面波ki照射到隨機粗糙面上時會發生散射，根據基爾霍夫近似理論，將粗糙面劃分為若干個近似平面的微面元，光波在微面元上發生菲涅爾反射.圖2是光波在微面元上反射時入射場與反射場的示意圖，θ為微面元上的光波入射角，θr=θ為微面元上的光波反射角，n為微面元的法向量，kr為反射波矢，Ei為入射場，Er為反射場，則微面元上的本地場E(r′)為入射場與反射場的疊加，即

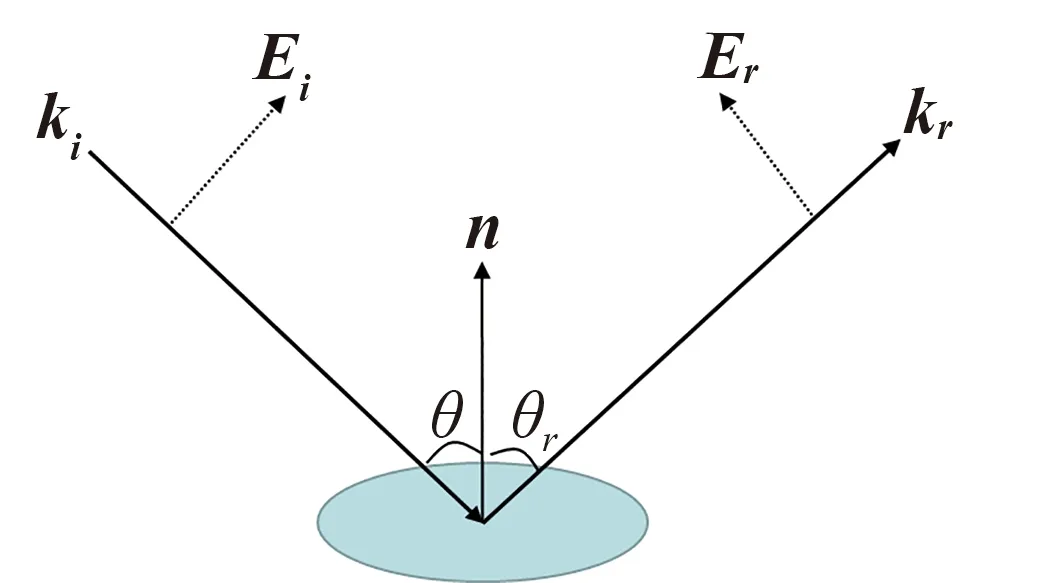
圖2 微面元入射場和反射場示意圖

E(r′)=Ei(r′)+Er(r′).

(4)

r′為微面元的位置矢量.借助于Stratton-Chu積分方程，可得到半球空間內任意位置的散射場[19]:

(5)

其中,r為空間某一觀察點的位置矢量，ds′為單個微面元面積，G(r,r′)為格林函數，其遠場近似形式為

(6)

其中，r為空間觀測點到原點的距離，ks為散射波矢，k為波數.

2 幾何遮蔽效應

利用式(4)得到的散射場包含了粗糙面所有面元的貢獻，忽略了有些面元可能沒有被照射到或無法被觀測到的情況，即面元的遮蔽效應，這些面元對散射場是沒有貢獻的，在入射角或散射角較大時遮蔽效應更加顯著，因此應該對粗糙面散射場進行遮蔽修正.

遮蔽效應包括入射遮蔽和散射遮蔽，入射遮蔽指由于粗糙面上的起伏使入射光被遮擋而無法照到的面元，散射遮蔽指由于面元反射的光線被其它面元遮擋而不能直接到達半球空間觀測點的面元，二者需要分開討論.

2.1 入射遮蔽效應

傳統的入射幾何遮蔽主要是基于射線追蹤法來計算被遮蔽的面元，即將光線認為是三維坐標系下的射線，通過追蹤射線與微面元是否相交來判斷哪些面元是被遮蔽的.如判斷微面元1是否被遮蔽的思路是：假設入射光線ki能照到面元1上，計算粗糙面上除面元1外所有面元是否與ki有交點，若有交點，則面元1被遮蔽，否則面元1沒有被遮蔽，如圖3中面元1被面元2遮蔽.這種方式雖然能夠很準確的判斷粗糙表面各面元被遮擋的情況，但時間復雜度較高.

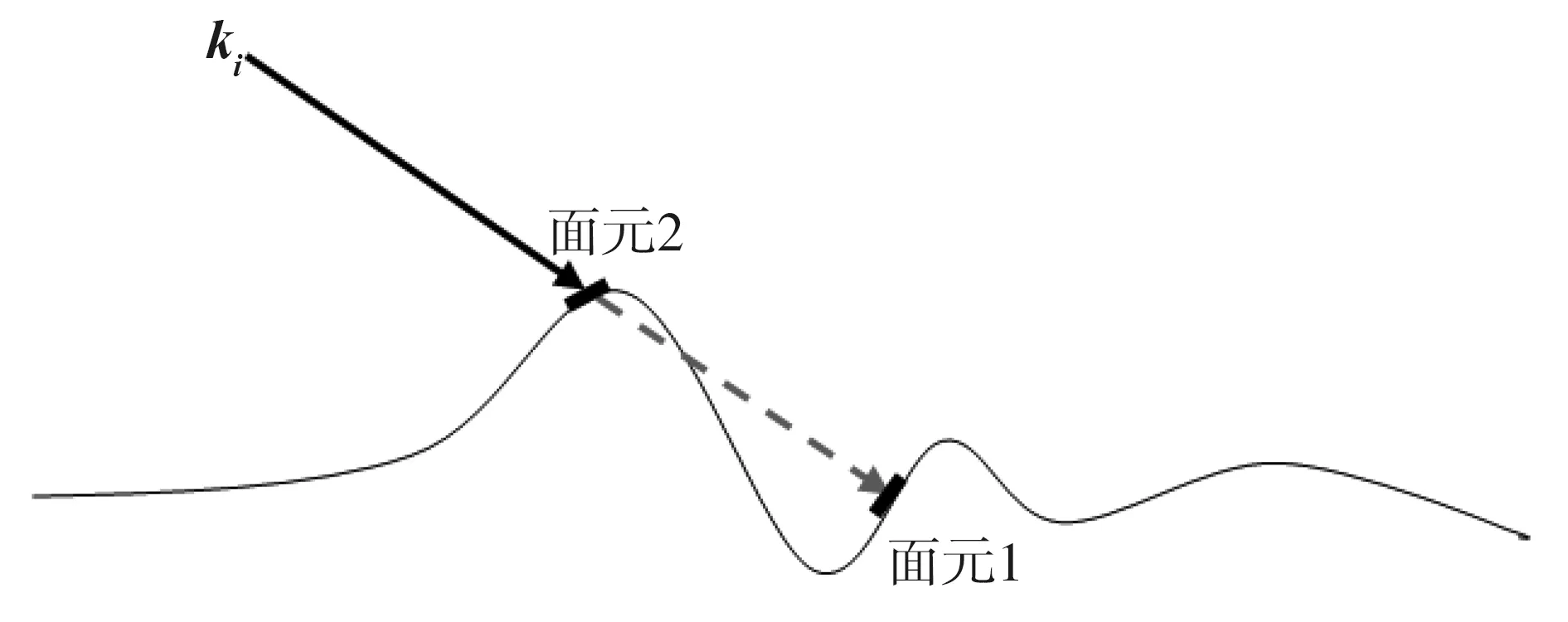
圖3 面元1被遮擋情況示意圖

設入射光線ki的方位角為0°，建立坐標系使xoz面為入射面，ki的方向指向x軸的正方向，z軸的負方向，因此二維隨機粗糙面的入射遮蔽效應可以轉化為一維粗糙面的遮蔽效應，如圖4所示.從圖中可以看出，入射光線在粗糙面上會產生陰影區，使陰影中的面元被遮蔽，每段遮蔽面元都起始于一個被照射面元和被遮蔽面元的“臨界面元”，如面元1，終止于入射到面元1的光線延長線與粗糙面的交點面元2，這段被遮蔽的面元都位于入射光線的下方，因此判斷一個面元是否被遮蔽，只要找出該面元在入射光方向最近的臨界面元，再判斷該面元是否在入射光線下方即可.

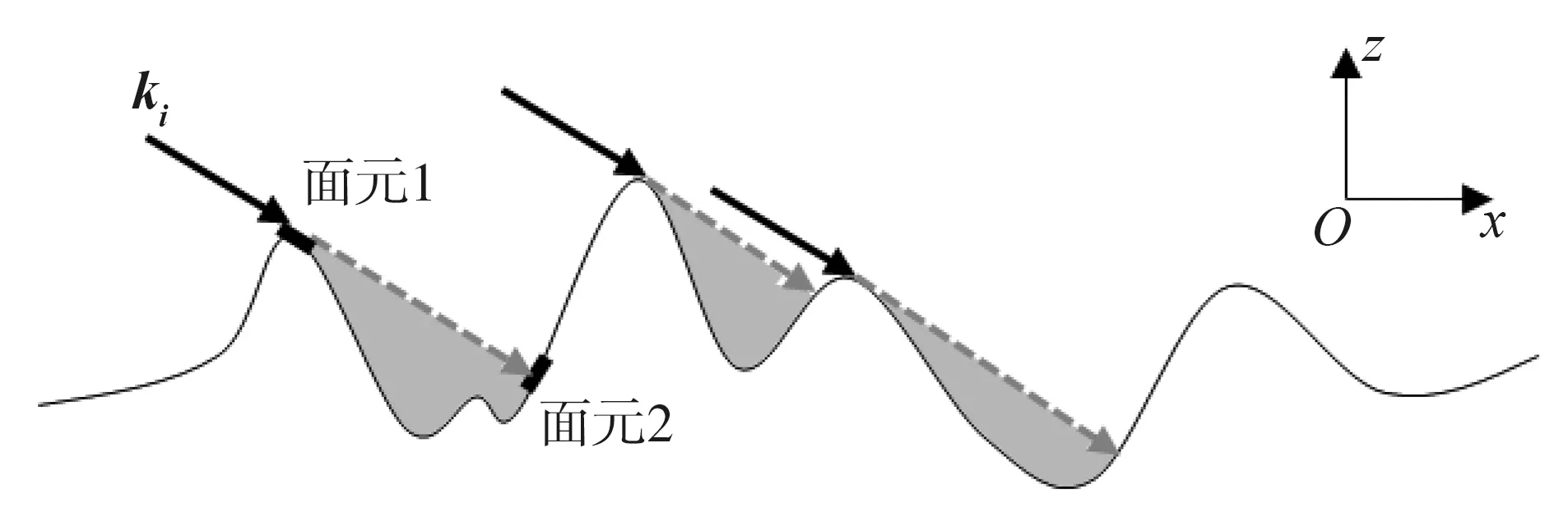
圖4 入射遮蔽效應示意圖

首先沿x正方向計算入射光線ki與每個微面元法線n是否滿足

ki·n=0.

(7)

若式(7)成立，那么該面元即為臨界面元.設臨界面元的坐標為(x1,z1)，則通過臨界面元的入射光線方程為

(8)

其中,kix和kiz為ki在x和z方向的分量，x和z為光線上的點.

設兩個相鄰臨界面元之間任一面元坐標為(x2,z2)，從臨界面元起沿x方向依次代入式(8)，若

(9)

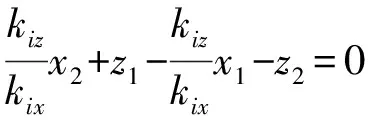
2.2 散射遮蔽效應

散射光線的方向可以為半球空間中的任意方向，因此應考慮二維粗糙面的遮蔽.傳統二維粗糙面光線追蹤法的思路是：判斷一個面元是否被遮蔽須遍歷除該面元及其相鄰面元以外的所有面元，求該面元的散射光線與其他面元是否有交點，若有交點，則該面元被遮蔽；否則沒有被遮蔽.

在實際的光線傳播過程中，散射光能夠經過的面元是有限的，如圖5(a)所示，ks是二維粗糙面上任意面元1的散射光，虛線代表散射光可能經過的面元.圖5(b)是二維粗糙面在xoy面的投影，其中,網格為粗糙面上各微面元的投影，k′s為ks的投影，陰影方框為k′s經過的投影面元.因此在計算其他面元是否對面元1的散射光線有遮擋只需判斷陰影投影面元對應的粗糙面面元對其是否有遮擋，若有遮擋，則面元1 被遮蔽，無需判斷粗糙面上除面元1以外的所有面元，可以大大減少計算量.

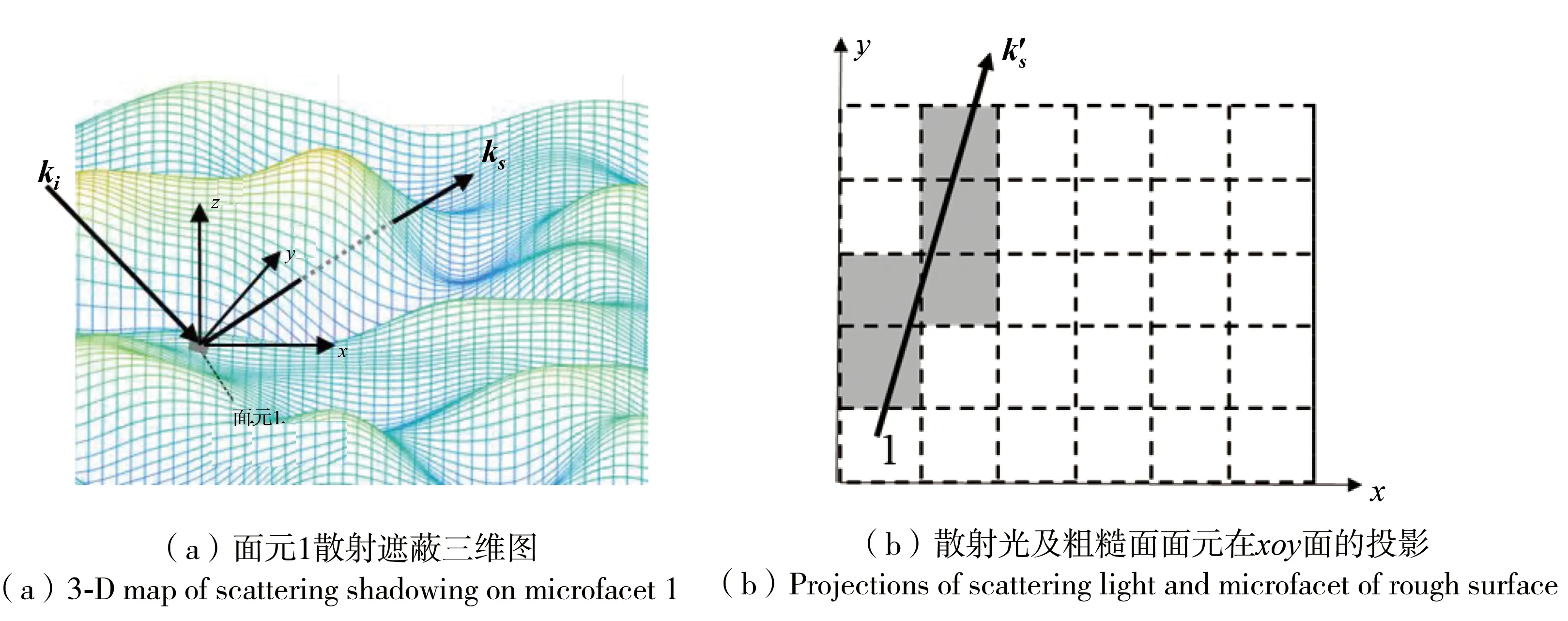
圖5 粗糙面散射遮蔽效應示意圖

首先，若散射光線ks與面元1的法向量n滿足ks·n<0，說明面元1的散射光不能直接發射到半球空間，面元1被遮擋.若ks·n≥0，則設k′s的斜率kxy為

(10)

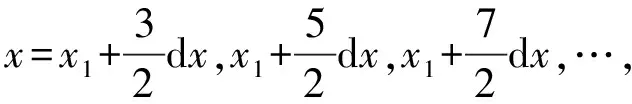
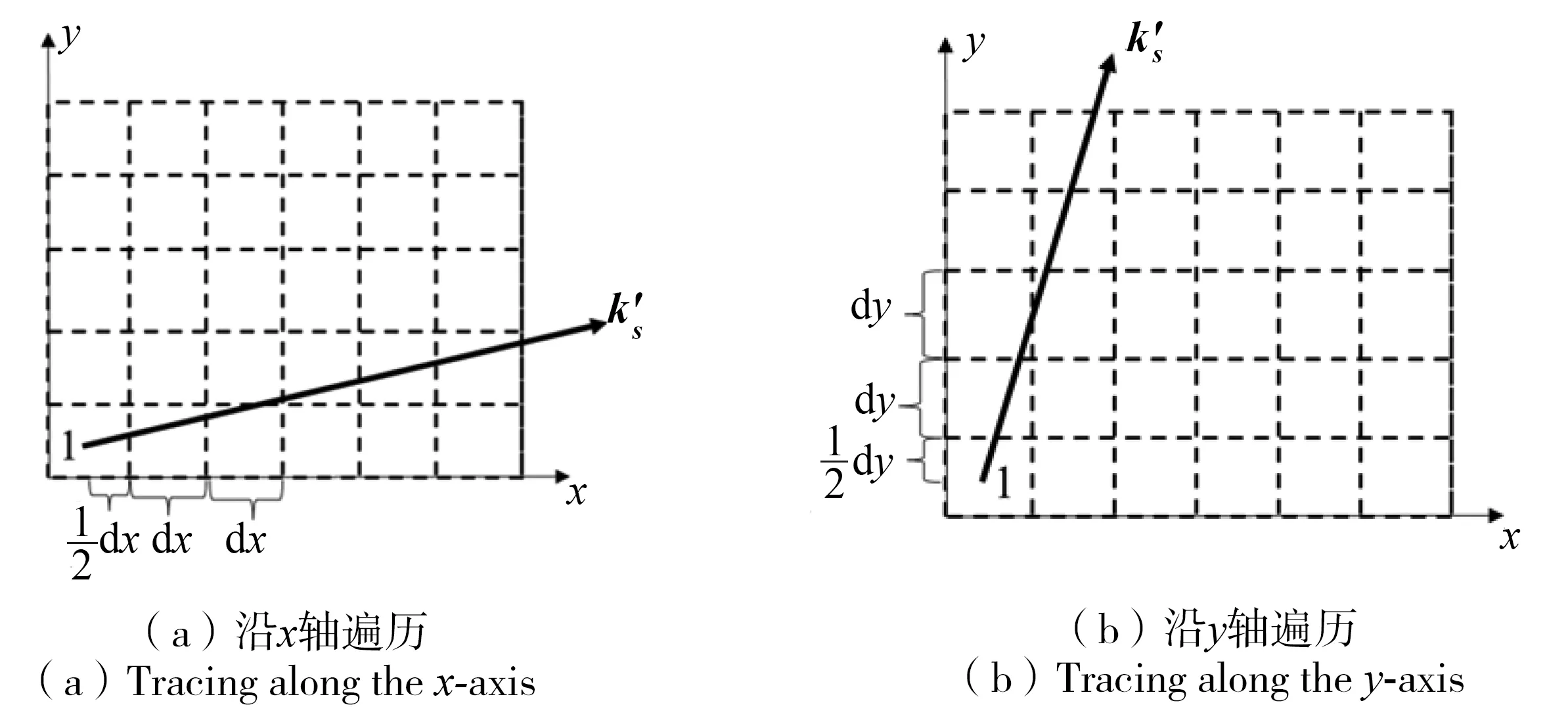
圖6 搜索k′s經過的面元

設面元1的坐標為(x1,y1,z1)，法向量為n=(nx,ny,nz)，面元1的散射光線為ks=(kx,ky,kz)，與k′s相交的投影面元對應的粗糙面面元2坐標為(x2,y2,z2)，法向量為n′=(n′x,n′y,n′z)，則面元1的散射光線方程為

(11)

面元2所在平面的平面方程為

(x-x2)n′x+(y-y2)n′y+(z-z2)n′z=0.

(12)

將式(11)和式(12)聯立可得到面元1的散射光線ks與面元2所在平面的交點c=(xc,yc,zc).若xc和yc滿足

(13)

則交點在面元(x2,y2,z2)內，說明面元1被遮蔽.

2.3 改進效果

選取lx=ly=4 μm、δ=0.5 μm的隨機粗糙面，計算入射角為θi=30°，散射角為θs=70°，散射方位角為φs=45°時的遮蔽效應，改進前與改進后的計算時間統計如表1所示，其中,N為x和y方向劃分面元數量，tx為原始算法的程序執行時間，ty為改進后算法的程序執行時間，運算平臺為i7-7500U CPU，頻率為2.90 GHz，內存為8 GB，編程軟件為matlab R2019b.

由表1可知，相對傳統射線追蹤算法，本文改進算法計算遮蔽效應的時間大大縮短，并且隨著粗糙面面元數量的增加，改進算法的優勢更明顯.

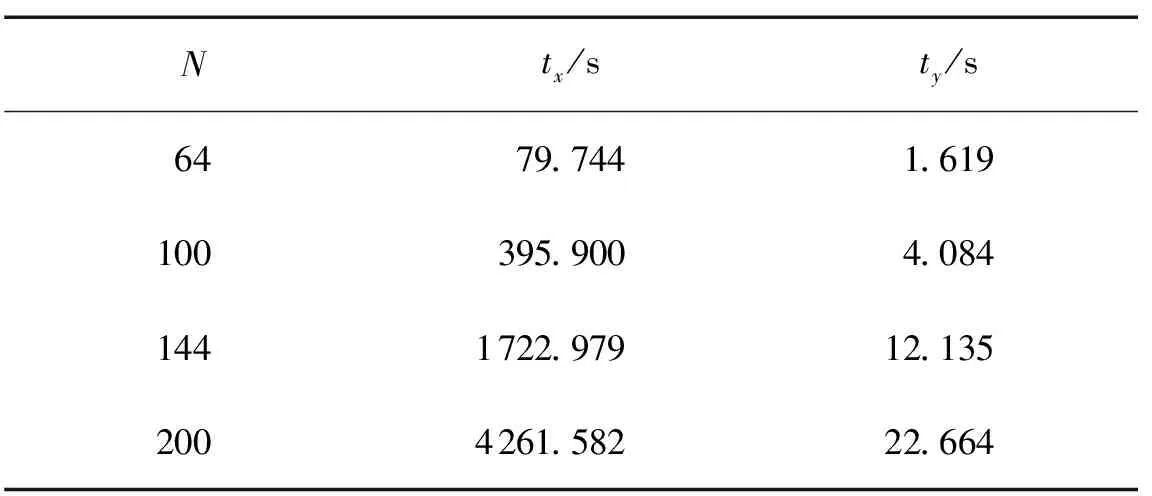
表1 改進后的程序執行時間

3 隨機粗糙面散射光強數值計算

選取lx=ly=4 μm、δ=0.4 μm的金屬鐵隨機粗糙表面為對象，當入射光波長為λ=0.905 μm時，金屬鐵的折射率為n=3.12+3.87i.根據式(4)和上述的遮蔽效應，分別模擬計算了S波、P波以30°角入射時，入射面內散射光強的分布，如圖7所示，圖中散射光強均歸一化到S波入射時散射光強的最大值.由圖可知本文模擬結果與文獻[20]的結果符合較好，說明本文提出的遮蔽效應計算方法是正確的.圖8給出了S波、P波30°角入射時半球空間散射光強的分布，可見半球空間中散射光強的分布是關于入射面(散射方位角為0°)對稱的，并主要集中在與入射光鏡像方向(即散射角為30°，散射方位角為0°)附近，散射角方向半寬度約40°，散射方位角方向半寬度約60°，近似在鏡像方向有最大值，P波散射光強小于S波散射光強.

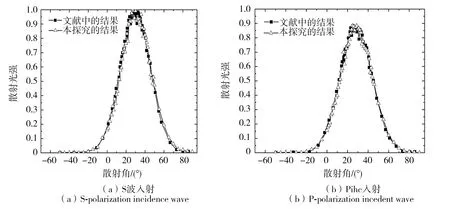
圖7 入射面內散射光強分布

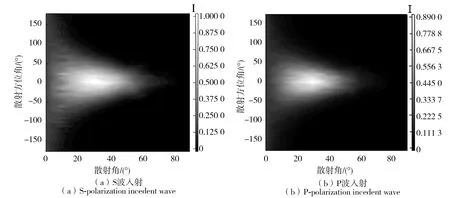
圖8 全角度散射光強分布

4 結 論

粗糙面在自然界中十分常見，對粗糙面的散射場進行深入研究在目標檢測、識別等領域具有重要意義.本文利用線性濾波法生成了不同相關長度和均方根高度的高斯型二維隨機粗糙面，采用基爾霍夫近似方法分析了隨機粗糙面的散射.針對傳統幾何遮蔽運算中時間復雜度高的問題，提出了幾何遮蔽的改進算法.對于入射遮蔽，判斷某一面元是否被遮蔽只要找出該面元在入射光方向最近的臨界面元，再判斷該面元是否在過臨界面元的入射光線下方即可.對于散射遮蔽，判斷面元是否被遮擋，只需要判斷該面元的散射光線與此散射光在粗糙面上投影所經過的面元是否有交點即可，無需判斷粗糙面上所有面元.入射遮蔽的時間復雜度由O(N4)(O為描述時間復雜度的函數)降為O(N2)，散射遮蔽的時間復雜度由O(N4)降為O(N3)，計算效率得到很大提升.模擬計算了S波和P波入射到鐵表面時入射面內散射光強的分布，與文獻結果進行對比，基本吻合，證明了改進后方法的有效性.計算了隨機粗糙面的全角度散射光強，結果表明散射光強分布關于入射面對稱，且主要集中在與入射光鏡像方向附近，散射角方向半寬度約40°，散射方位角方向半寬度約60°，P波散射光強小于S波散射光強.研究結果能夠為目標探測提供理論參考.