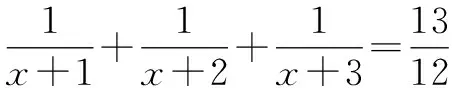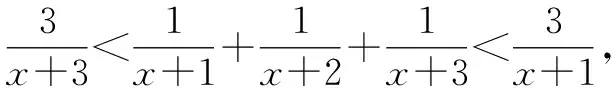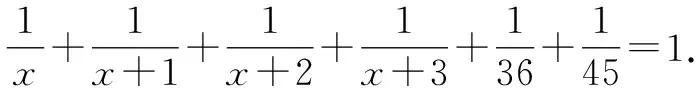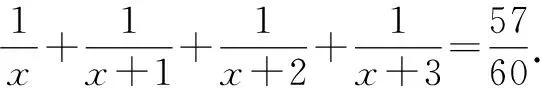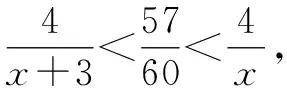初中數學解題中放縮法的運用分析
?江蘇省南京市第八中學 李鳴午
在最近的初中數學競賽題乃至教材(比如蘇科版等)中都陸陸續續出現了借助于放縮法理論工具進行解答的試題.可見,放縮法在初中數學解題中的重要性愈來愈明顯.筆者結合具體的例子嘗試著對放縮法在初中數學中的具體運用展開分析,歸納提煉出解題的方法及思考路徑.通常而言,把代數式子的某個具體項或是某一項所涉及到的某個具體因式加以放大或是縮小處理即不等取代,從而使它向結論的方向轉化的一種數學方法,叫“放縮法”.比如,在證明A 放縮法在初中數學不等式習題中是常用的一種方法.借助于放縮法的特性,可以巧妙地化解有關不等式的證明問題[1]. 綜上所述,原不等式成立. 初中數學問題中,有一類習題是關于最值的問題.一般情況下,當難以順利地確定出最大值或者最小值時,合理運用放縮法,便可以有效化解這一類最值問題. 例2已知二次函數y=x2+ax+b的圖象和x軸2個交點對應的橫坐標依次是m,n,同時|m|+ |n|≤1.假定與上述的條件相吻合的b對應的最大、最小值依次是P,Q,試求|P|+ |Q|的數值[2]. 解:由m,n為一元二次方程x2+ax+b=0的2個實根,根據韋達定理,可知m+n=-a,mn=b. 又|m+n|≤|m|+|n|≤1,|m-n|≤|m|+|n|≤1. 由于原方程式存在實數根,因此Δ≥0,也就是a2-4b≥0. 初中數學習題中,經常遇到有關完全平方數的問題.由于完全平方數本身具有性質上的獨特性,如果能夠有意識地把握住這一點,同時合理運用好放縮法這一工具,能夠使這類問題迎刃而解[3]. 例3求使m2+m+7屬于完全平方數的全部整數m的值. 解析:(1)如果m≥7,那么m+7≤2m. 因此,m2+m+7處于2個連續的整數的平方之間,而非完全平方數. (2)如果0 (3)如果m=0,那么m2+m+7的值為7,非完全平方數. (4)如果m<0,那么使n=-m,由于n為正整數,因此m2+m+7=n2-n+7.就二次三項式n2-n+7而言,如果n>7,那么-n<-7,且有-n+7<0.也就是n2-n+7 如果n≤7,將n=1,2,3,4,5,6,7依次代入到n2-n+7中,通過運算可以發現,僅僅在n=2或7的時候,n2-n+7屬于完全平方數.因為n=-m,所以m=-2或-7. 綜上所述,與條件相吻合的整數m的值分別為1,6,-2,-7. 上述問題的化解,不僅僅使同學們掌握了借助于放縮法判斷單個整數是否屬于完全平方數的手段,同時訓練了數學思想方法中重要的分類討論法.對上述問題還能夠進行以下的變式練習:當n為自然數時,求證4n2+4n+4不可能屬于完全平方數. 初中數學習題中,不定方程問題相對比較復雜,如果按部就班地求解,步驟顯然會變得非常繁瑣.此時,恰當地使用放縮法可以達到事半功倍的效果[4]. 綜上所述,方程的正整數解是x=1. 事實上,上述有關不定方程的相關問題能夠進一步推廣到以下例子. 由x>0,可得 由于x為正整數,因此x=2,3,4. 通過檢驗x=3符合題意. 故a=3,b=4,c=5,d=6. 綜上所述,基于以上4個不同的初中數學題型的探討及其解答,不難發現放縮法在初中數學解題教學中具有非常重要的作用.按照中學數學課程標準中“要培養學生分析問題和解決問題的能力”的相關要求,在初中數學教學中,應有意識地培養數學思想方法的有效運用,并達到創新性使用的目的.因此,通過放縮法的運用,有意識地培養學生的“應用數學意識”,并落實到初中數學解題的教學中去,使學生了解數學的廣泛應用,從而提高學生對數學學習的興趣,并逐步形成運用數學知識解決問題的良好習慣.1 不等式問題中放縮法的運用


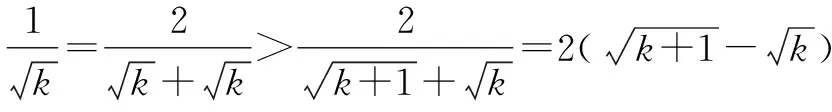
2 最值問題中放縮法的運用



3 完全平方數問題中放縮法的運用
4 不定方程問題中放縮法的運用