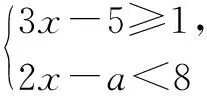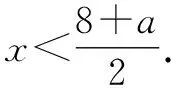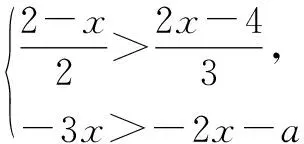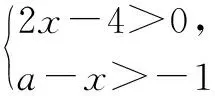含參一元一次不等式(組)問題求解策略
?山東省廣饒縣英才中學 徐樹光
1 引言
若一個不等式中除了含有未知數以外,還含有其他字母,則稱這個不等式為含參數的不等式.一般解題策略是先把不等式化為一邊是未知數,另一邊是數字或含參數的表達式,再根據題目的其他條件對表達式的正負情況討論解答.下面以2020年中考題為例探求含參一元一次不等式(組)問題的求解策略[1].
2 直接使用口訣
由兩個一元一次不等式構成的不等式組,共有四種情況.已知a 利用這個口訣,有時可以快速解題. 因此應填:a≥1. 點評:用口訣解“不等式組有解或無解”問題比較方便,但需要注意解集中等號的取舍,這對初學不等式的學生是一個難點.對此類問題還可以作以下變式: 由于參數的存在,各不等式解集端點的值大小關系待定,用分類討論作答,可看出不同情況下的解集,符合題意的范圍即為要求的答案. 當a=2時,原不等式組的解集是x>1; 當a<2時,原不等式組的解集是x>1. 所以a的取值范圍是a≤2. 點評:分類討論將所求問題細化,多次使用口訣解答,找到滿足題意的參數的范圍;同時,也排除了不合題意的參數范圍. 不等式中的參數問題本質是在運動與變化中尋找滿足題意的范圍,有時臨界點較多,利用數形結合可以使問題直觀形象,降低思維難度,尤其對等號的取舍有重要的支撐作用. 例3(2020年天水改編)若關于x的不等式3x+a<2的最大整數解為2,則a的取值范圍是. 圖1 圖2 圖3 因此,a的取值范圍是-7≤a<-4. 點評:數軸是數形結合的有力工具,利用數軸將不等式的解集直觀表示出來,可以快速準確地建立含參不等式,對難于抉擇的端點也可一目了然. 當一個問題有多種可能性,或不易直接解答,可從問題的反面分析研究,即利用補集思想解決. A.m>-1 B.m≥-1 C.m≤-1 D.m<-1 解析:解不等式組,得x>1,且x≤-m.考慮從反面出發,求原不等式組無解時,a的取值范圍.由前面的口訣,知-m≤1,即m≥-1時,原不等式組無解,即不等式有解的范圍是m<-1.故選:D. 點評:正難則反是一種重要的思維方式,巧妙運用這個策略,適當轉變思路,嘗試逆向思維對題目進行分析,能夠降低思維難度,減少運算量. 不等式中有關取值范圍的問題,對端點的取舍容易出錯,因此對于一些選擇題,只需把端點處理好,采取端點驗證法,可以減少運算量. A.0≤a≤2 B.0≤a<2 C.0 解:從選項中發現,解決本題的關鍵在于0和2是否可取. 由3x-5≥1,得x≥2. 當a=0時,不等式組的解集是2≤x<4,有兩個整數解,不合題意,所以舍去a=0.排除A,B選項. 當a=2時,不等式組的解集為2≤x<5,有三個整數解,符合題意,所以a=2可取. 因此應選:C. 點評:對于一個數學問題,能直接解答固然很好,而從不同角度思考問題,特別在考試的有限時間內快速得出答案,既可節省時間,又可提高正確率,是非常有益可取的做法. 以上含參不等式的五種求解方法,要因題而異,根據題設靈活選用,尤其是等號的處理,要正確理解.下面讓我們運用這幾種方法大顯身手吧! A.a≥2 B.a<-2 C.a>2 D.a≤2 解析:解不等式組得x<2且x 解析:解不等式組,得x>2且x 解析:解不等式組,得x<4-a且x>-1.則不等式組有解時,滿足-1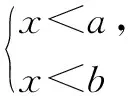
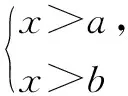
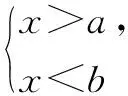
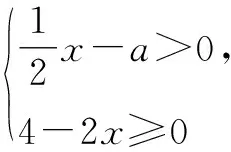
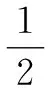
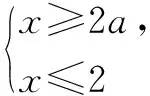
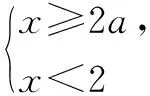
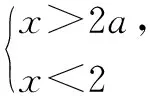
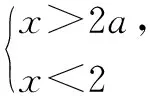
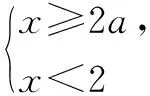
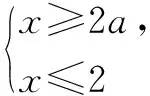
3 分類討論
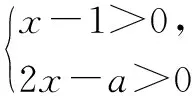
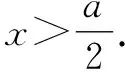
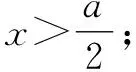
4 數形結合
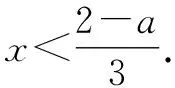
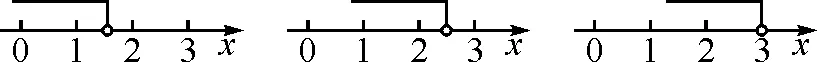
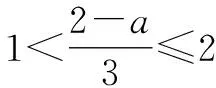
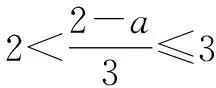
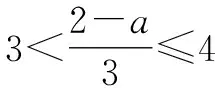
5 補集思想
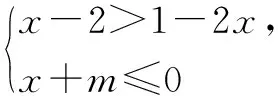
6 端點驗證