初中學生數學解題錯誤的案例研究
?廣州市玉巖中學 李小兵
《義務教育數學課程標準》明確要求,教師要耐心地引導學生分析錯誤產生的原因,并鼓勵他們自己去改正,從而增強學習數學的興趣和信心.因此,關注初中學生數學學習中出現的問題,盡可能幫助學生避免或減少解題錯誤并予以糾正,能夠有效地提高初中數學課堂教學質量.
1 知識性錯誤
知識性錯誤是指對概念及定理的認識模糊不清或錯誤運用公式與法則導致的錯誤;基本技能不熟練,運算基本功不扎實,遺漏或隨意添加條件導致的錯誤;等等.
1.1 概念不清
概念是學生思維的基本形式,也是解題的重要依據.學生在解題過程中由于對概念、規律的內容認識不清或不能正確理解它們的確切含義而產生的一些錯誤就是概念性錯誤.
例1下列方程哪些是一元二次方程?
(1)ax2+bx+c=0;
(2)x2=0;
(4)2x2-x-1=0;
(5)3x(x-1)=3x2+1;
(6)(1-m)x2+mx-2=0.
錯解:(1),(2),(3),(4),(5),(6).
分析:例1中對一元二次方程概念的理解,特別容易忽視方程ax2+bx+c=0中系數a,b,c的限制條件.授新課時應講明——(1)a≠0,b,c為常數;(2)三種特殊形式,即ax2=0(a≠0),ax2+bx=0(a≠0,b為常數),ax2+c=0(a≠0,c為常數);(3)方程要先化簡為一般形式,牢牢抓住二次項系數a≠0.
1.2 法則不明
初中代數法則多、公式多且易混、易錯.學生運算出現問題往往是公式記憶錯誤,運算法則混淆等.
例2計算:(1)(-4)2=,-22=;(2)(3x-2)2=.
錯解:(1)-8 ,4;(2)9x2-4
分析:例2(1)錯解的原因是將乘方的運算法則與數的運算法則相混淆了.例2(2)中把乘法公式中完全平方公式和平方差公式記混淆了.
2 邏輯性錯誤
邏輯性錯誤主要表現為推理欠嚴密,條理不清,自相矛盾.有些學生思維發展水平低,推理能力弱,數學知識、能力、方法儲備不足,推理思路不明,從而得出不準確的結論[1].
2.1 變形不恒等
把代數式當等式來變形、化簡.

錯解:原式=2(x-2)-2(x+2)=2x-4-2x-4=-8.
分析:對于例3,學生在進行分式計算時,易將代數式的變形與等式的變形混在一起,錯誤地將分式轉化為整式,從而違背恒等變形這個原則.
2.2 混淆“或”與“且”
“或”表示選擇的關系,二者必居其一.“且”表示同時滿足.在使用“且”和“或”時不能混為一談.


x2+4x+3≠0.
整理,得(x+3)(x+1)≠0.

分析:例4中,當x=-3或x=-1時,分母都等于零.要使分式中的分母不等于0,則x既不能等于-3也不能等于-1,兩者是一個并列的關系,所以應該用“且”.
2.3 偷換命題
學生在運用三角形中位線定理、等腰三角形三線合一性質、垂徑定理解題時,往往將性質或判定的題設和結論混淆,導致論題改變,發生錯誤.
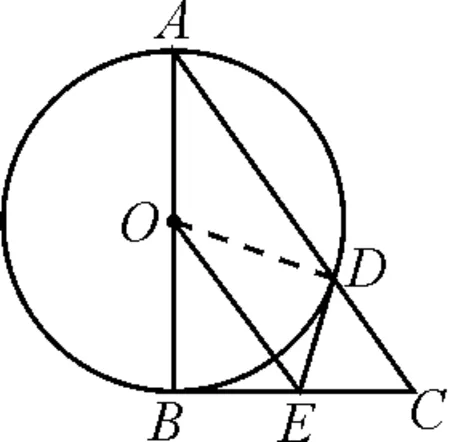
圖1
例5如圖1,⊙O是Rt△ABC中以直角邊AB為直徑的圓,⊙O與斜邊AC交于點D,過點D作⊙O的切線DE交BC于點E.求證:OE是Rt△ABC的中位線.
錯解:連結OD.
∵∠ABC=90°,AB為直徑,
∴EB是⊙O的切線.
又∵DE是⊙O的切線,
∴∠BOE=∠DOE.
∴∠BOD=∠BOE+∠DOE=2∠BOE.
又∠BOD=2∠A,
∴∠BOE=∠A.
∴OE∥AD.
∵O是AB的中點,
∴OE是△ABC的中位線.
分析:三角形中位線定理是由E是BC的中點和O是AB的中點得出OE∥AD.例5中由OE∥AD和O是AB的中點得出OE是△ABC的中位線,顯然是沒有正確認識三角形中位線定理,但可進一步由平行線分線段成比例定理得出E是BC的中點.
3 策略性錯誤
策略性錯誤是指考慮不周全導致解題思路受阻或解題方向錯誤,或選擇非最優解法明顯增加了解題的難度與出錯機會,使得問題最終得不到解決.
3.1 忽視題目中的隱含條件
解題時有些條件隱含于已知條件或圖形中,但由于學生馬虎大意,未深刻把握數學的嚴謹性要求,忽視題目中的隱含條件以致得出錯誤結論.
例6已知關于x的方程x2-2(k-1)x+k2=0有兩個實數根x1,x2,且x1+x2=x1x2-1,求k的值.
錯解:由題意可得x1+x2=2(k-1),x1x2=k2.
所以-2(k-1)=k2-1.
解得k1=1,k2=-3.
分析:對于含字母系數的一元二次方程或二次函數的問題,學生往往忽略考慮二次項系數不為零、根的判別式Δ≥0等隱含條件,因考慮不周全出錯.例6中求k的值要進一步檢驗根的判別式.
3.2 忽視“分類思想”造成漏解或錯解
解題時,如遇到等腰三角形、相似三角形或動點、動直線問題,常常要分類討論所有可能情況,否則答案不完整.
例7在平面直角坐標系xOy中,點P在x軸上,點A(1,1).若△AOP為等腰三角形,請求出點P的坐標.
錯解:滿足條件的等腰三角形AOP的點P坐標為(1,0)和(2,0).
分析:應分三種情況討論.
(1)當AO=AP時,以A為圓心,AO為半徑作圓與x軸的交點即為點P,則P(2,0);
(2)當OP=AP時,作OA的垂直平分線,交x軸的于點P,則P(1,0);
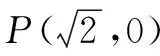
3.3 解題方法繁瑣造成錯誤
同一道題,不同的解題思路或輔助線作法對解題有不同的影響,有的會直接增加題目的計算量和難度,有的會導致思維障礙解不出來.
例8如圖2,四邊形ABCD是正方形,點E是邊BC的中點,∠AEF=90°,且EF交正方形外角平分線CF于點F.求證:AE=EF.
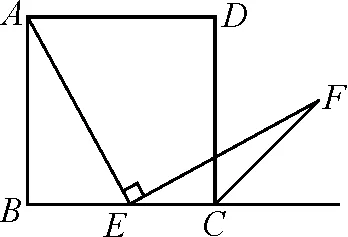
圖2

圖3
證法1:如圖3,取AB的中點M,連結EM.可證△AEM≌△EFC(ASA),從而得AE=EF.

圖4
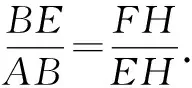
分析:上述兩種方法雖然都通過作輔助線利用全等證出線段相等,但顯然證法1更簡單,證法2在尋找全等的條件時難度更大,實際操作中學生會因缺全等條件而半途而廢.
4 心理性錯誤
心理性錯誤主要表現為缺乏堅強的意志和信心,導致解題出錯的急躁心理現象.良好的心理素質,可以克服心理障礙而減少錯誤.
4.1 解題思維定式,思維慣性
有些數學題目在形式上相似,在解法上也雷同.學生解題時容易產生慣性思維,“先入為主”匆忙下結論,因負遷移而導致錯誤.
例9解一元二次方程x(x+2)=3x.
錯解:將方程兩邊除以x,得(x+2)=3.
所以,此方程的解是x=1.
分析:例9中方程兩邊同時除以x的前提條件是x≠0,而x=0恰好是此方程的一個解.憑經驗約分造成漏解.
4.2 思維抑制或情緒焦慮
心理學的研究表明,考試中學生臨場過分焦慮,心理壓力過大以致于出現暫時性思維障礙,稱為思維抑制.考試中,遇到運算數字較大的計算或不熟悉的題型一時找不到思路,就會產生焦慮,有時產生暫時的遺忘,干擾思維的正常運行,導致會而不對,對而不全.
例10已知二次函數y=mx2+(1-2m)x+1-3m與x軸相交于不同的兩點A,B.
(1)證明此二次函數的圖象一定經過一個定點P,并求出點P的坐標.


分析:例10證明過定點、求最值問題因不常見往往使學生望而卻步,心理上有思維障礙.
4.3 審題馬虎、理解膚淺
粗心大意源于不良的學習習慣.審題是解題的關鍵,許多學生在審題時粗心大意,經常看錯題或看漏條件,沒能正確地理解題意導致錯誤的產生.
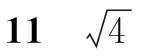
錯解:選A.
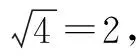
德國哲學家黑格爾曾說過:“錯誤本身乃是達到真理的一個必然的環節.”錯題,既是學生積累學習經驗和學習資料的寶庫,又是教師發現教學問題、改進教法、及時調整教學策略的重要手段[2].因此,利用好錯題資源,分析產生錯誤的原因,總結解題經驗,就一定能提高數學解題水平.

