耗散型隨機非線性薛定諤方程的隨機共形多辛方法

苗利軍，陳紅宇

(遼寧師范大學 數(shù)學學院, 遼寧 大連 116029)

對于隨機偏微分方程，解析解的推導是十分困難.因此，數(shù)值方法成為研究方程解析解的有力工具.為了保證數(shù)值解長期模擬的可靠性和有效性，數(shù)值方法應盡可能地保持原始系統(tǒng)的固有性質(zhì).耗散型隨機非線性薛定諤方程[1]是一類特殊的隨機偏微分方程,具有隨機共形多辛幾何結構，在非線性光學和等離子體物理等領域都有重要應用.近幾年，構造數(shù)值格式保持耗散型隨機非線性薛定諤方程的幾何結構越來越受到學者們的廣泛關注，例如:Hong等人[1]研究了耗散型隨機非線性薛定諤方程的隨機共形多辛方法，文獻[2]提出了乘性噪聲驅(qū)動的隨機非線性薛定諤方程的隨機共形多辛守恒律，并構造數(shù)值格式保持該系統(tǒng)的隨機共形多辛幾何結構.受以上文章的啟發(fā)，本論文將構造數(shù)值格式來保持加性噪聲驅(qū)動的耗散型隨機非線性薛定諤方程的隨機共形多辛幾何結構.

1 耗散型隨機非線性薛定諤方程

考慮以下加性噪聲驅(qū)動的耗散型隨機非線性薛定諤方程[3]:

(1)

其中，λ=±1，耗散系數(shù)a>0，ε為噪聲尺度，復值Wiener過程W(t)是定義在給定的賦σ-域流的概率空間(Ω,F,{Ft}t≥0,P)上的Q-Wiener 過程.

記v=px，w=qx，z=(p,q,v,w)T，上述方程可以轉(zhuǎn)化為如下形式

Mdtz+K?xzdt=-aMzdt+?S0(z)dt+?S1(z)°dW1+?S2(z)°dW2，

(2)

其中，

以及“°”表示方程在Stratonovich型隨機積分意義下成立.

定理1.1[1]方程(2)滿足隨機共形多辛守恒律

dtω(t,x)+?xκ(t,x)dt=-aω(t,x)dt，

(3)

即

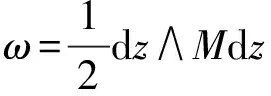
注1如果a=0，ε≠0，隨機共形多辛守恒律(3)為隨機多辛守恒律[4]:

dtω(t,x)+?xκ(t,x)dt=0.

注2如果ε=0,a≠0，隨機共形多辛守恒律(3)為共形多辛守恒律[5-6]:

dtω(t,x)+?xκ(t,x)dt=-aω(t,x)dt.

注3對于方程(1)，當a=0,ε=0時，確定的非線性薛定諤方程滿足多辛守恒律[7]:

命題1.1對任意a>0，下面的等式成立：

dt(eatω(t,x))+?x(eatκ(t,x))dt=0.

證式(3)兩邊同時乘以eat有

eatdtω(t,x)+eat?xκ(t,x)dt=-aeatω(t,x)dt，

則

[eatdtω(t,x)+aeatω(t,x)dt]+eat?xκ(t,x)dt=0，

從而

dt(eatω(t,x))+?x(eatκ(t,x))dt=0.

2 隨機共形Euler box格式

引入微分算子

基于文獻[6]，構造耗散型隨機非線性薛定諤方程(1)的隨機共形Euler box格式:

(4)

其中,

定理2.1隨機共形Euler box格式(4)具有離散的隨機共形多辛守恒律:

(5)

證將式(4)變形為

(6)

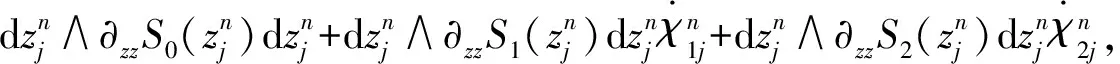
而上面等式左邊的前兩項

左邊的后兩項

因此，

(7)

故

命題2.2對任意a>0，下面的等式成立：

證式(7)的兩端同乘eatn，得到

則

因此