GaAs多線切割切片翹曲度的有限元分析
康洪亮
(中國電子科技集團公司第四十六研究所,天津 300220)
翹曲度(Warp)是描述晶片加工質量的一個重要幾何參數。翹曲度定義為切片的中心平面與基準參考平面之間的最大距離與最小距離之差。翹曲度屬于體缺陷,除在晶體生長中調整熱場和拉晶參數外,切片線切工藝中鋼線張緊力、鋼線速度、進給速度、鋼線線徑、溫度等都會影響翹曲度,研究線切工藝參數與切片翹曲度間關系,對于控制切片翹曲度具有重要意義。科研生產中當切片翹曲度指標超標時,需對影響翹曲度的工藝參數進行全面的分析研究,開展工藝試驗,耗資費時。因此極有必要研究兩者之間的理論關系,為優化相應工藝參數,達到快速改善切片翹曲度的目的。采用Abaqus軟件對砷化鎵晶棒線切過程進行有限元建模分析,在有限元模型中,晶片總厚度偏差為零,即可將未變形前切片面視為基準面,切片面受熱變形后的平面視為中心平面。采用切片表面節點變形位移來間接反映切片翹曲度。
1 多線切割熱分析理論基礎
研究多線切割過程中的熱力學問題主要包括兩方面內容:傳熱問題分析,確定模型的線切溫度場;熱應力問題,確定模型的應力應變場。結合鍍銅鋼線鋸切割砷化鎵晶棒時,溫度場直接影響切片熱應力應變場,而熱應力場對溫度場耦合影響幾乎可忽略,因此本文對砷化鎵晶棒線切熱分析選用Abaqus順序耦合熱應力分析法。
1 多線切割溫度場分析基礎理論
線切過程中砷化鎵晶棒的溫度隨熱載荷移動重新分布,線切溫度場與熱載荷加載時間有關,因此屬于非穩態傳熱。
1.1 溫度場數學模型
線切過程中,熱源位置是變化的,根據傅立葉傳熱定律與能量守恒定律,建立砷化鎵晶棒線切過程中無內熱源三維傳熱瞬態溫度場的微分方程:
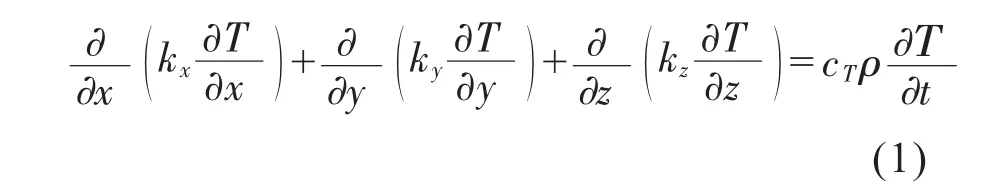
式(1)中,kx、ky、kz分別為砷化鎵晶體沿x、y、z方向的熱傳導系數;cT、ρ分別為晶體的比熱容、密度;T為晶體溫度。
式(1)左端表示由x、y、z方向傳入晶體的熱量,右端表示晶體升溫所需熱量。
在求解域(Ω)的溫度場分布應滿足的邊界條件。邊界條件分如下三類:
第一類邊界條件Γ1(給定溫度值),是強制邊界條件:
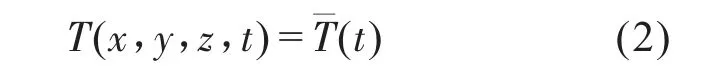
第二類邊界條件Γ2(給定熱流密度):

式(3)中,qv為切口表面上的熱流密度,nx、ny、nz為邊界外法線的方向余弦。
熱流密度為物體單位面積橫截面在單位時間內通過的熱量。對于線切加工的熱流密度大致可以理解為施加在單位面積上的功率[1-4]:

式(4)中,P為線鋸切割功率,ξ表示線鋸切割能量損耗系數,為無量綱量,A為切口橫截面積。線鋸切割功率P可表示為鋼絲張緊力與鋼絲運動速度的乘積:

根據線鋸切割加工原理得到線切能量損耗系數ξ可以近似表示為:

式(6)中,α為鋼絲的弓角。
每一分析步材料切除層體積V可以近似表示為[1]:

式(7)中,L為鋼絲與工件接觸長度;d為切口寬度;h為每一分析步晶體進給長度。
因此,把式(5)和式(7)代入式(4)便可得到線切加工中的熱流密度[1-3]:
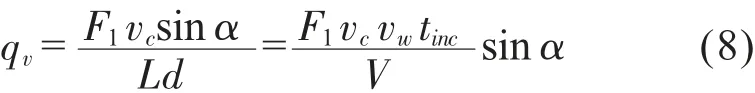
式(8)中,vw為晶體進給速度;tinc為每一分析步時間。
第三類邊界條件Γ3(給定對流換熱系數):
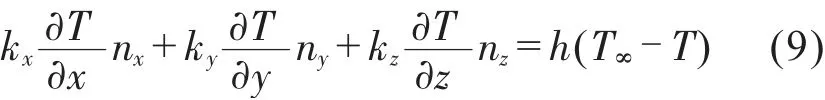
式(9)中,h為對流換熱系數,自然對流換熱系數與強制對流換熱系數其值有所不同。
1.2 熱應力分析基礎理論
砷化鎵晶體為脆性材料,本文不考慮其塑性,根據熱彈性力學理論。當物體內部溫度的分布不均會引起部件熱脹冷縮,在部件內部產生熱應力,依據線性熱力學理論,物體內部微元體的總應變由溫度變化引起的應變和應力引起應變兩部分組成。則由溫差ΔT引起的應變為εfij=[α]ΔT,總應變εij為:
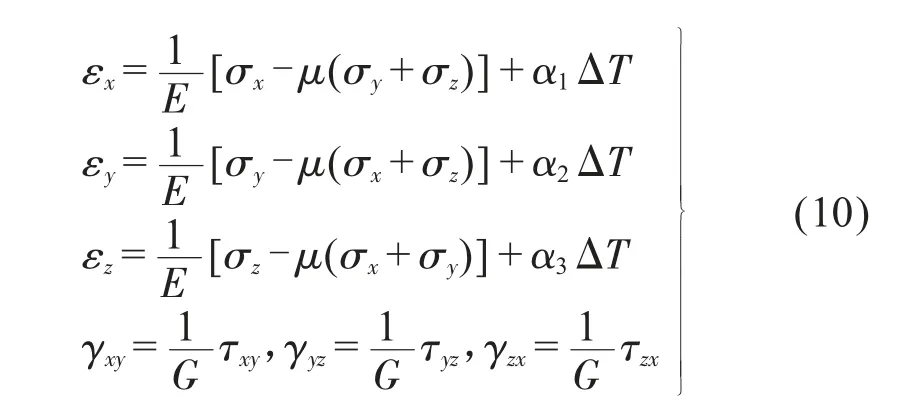
式(10)指標形式為:
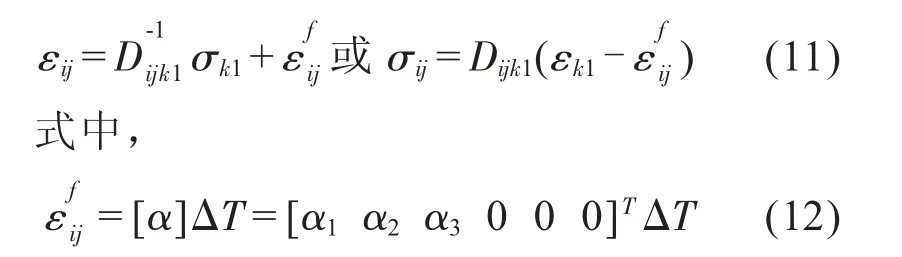
除了物理方程與普通的彈性問題有所不同,熱應力問題的平衡方程、邊界條件以及幾何方程均相同,根據虛功原理δU-δW=0得:

將結構離散化求變分,最后得到單元節點力與節點位移關系式:

式(14)中:pfe為溫度等效載荷。由于溫度場直接影響切片熱應變場,而熱應變場對溫度場的耦合影響幾乎可忽略不計,因此本文選擇順序耦合熱應力應變有限元分析模型。
2 砷化鎵晶棒多線切割熱分析有限元模型建立
首先建立砷化鎵晶體線切溫度場三維有限元模型,采用生死單元算法來模擬材料去除,通過施加動態載荷步來模擬熱載荷的移動,在切口表面和新形成線切晶面設置為強迫對流換熱邊界,在晶體外表面設置為自然對流換熱邊界,如圖1所示。

圖1 砷化鎵晶棒多線切割Abaqus有限元建模示意圖
圖1為砷化鎵晶棒多線切割Abaqus有限元建模示意圖。其中分析步類型設置為General:Heat transfer(Transient),在Interaction功能模塊中設置對流換熱邊界,在“預定義場”中設置初始溫度邊界條件為室溫22℃,模型選用DC3D8(八節點隱式線性熱傳導單元)。
然后進行熱應力分析,將溫度場結果作為邊界條件,刪除之前定義的分析步和“預定義場”。分析步類型設置為General:Static,General,“預定義場”,在Load模塊中Create Predefined Field,選定類別Other中Temperature,在Distribution里選擇From results or database file:File name:導入文件名,文件為之前溫度場結果文件,單元類型選擇C3D8L(八節點六面體線性非協調模式單元)。
本文在計算熱載荷qv時,室溫設為22℃,鋼絲速度為5 m/s、晶棒進給速度為0.15 mm/min,鋼絲張緊力為20 N、鋼絲弓角為1.5°。晶體表面與空氣的自然對流換熱系數一般為1~10 W/(m2·℃),與冷卻液的強迫對流換熱系數為1×l04~3×l04W/(m2·℃)。但隨著切割深度的不斷增加,冷卻液進入切縫的能力也在逐漸變化,參考文獻[1]并結合實驗,切縫中的對流換熱系數可歸納為:
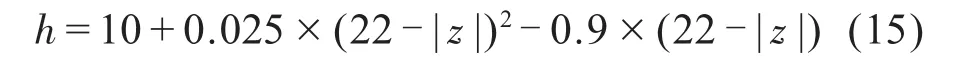
式(15)中,z為切割深度坐標,原點在晶棒圓心。
砷化鎵晶棒材料屬性見表1。
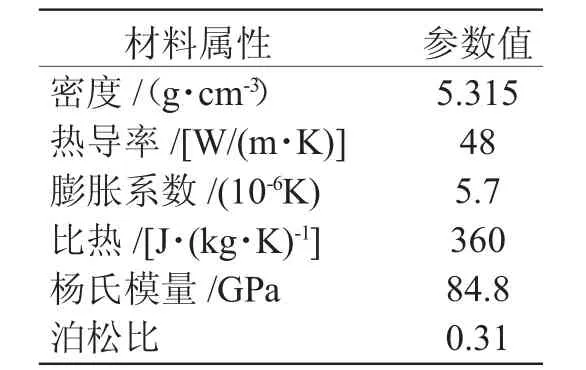
表1 砷化鎵晶棒材料屬性
3 熱分析仿真結果分析與討論
3.1 鋼絲張緊力對翹曲度影響
在鋼絲速度vc=5 m/s,晶棒進給速度vw=0.15 mm/min,鋼絲線徑d=0.12 mm時,通過改變式(8)中張緊力F1,分析鋼絲張緊力與切片翹曲度之間關系,如圖2所示。
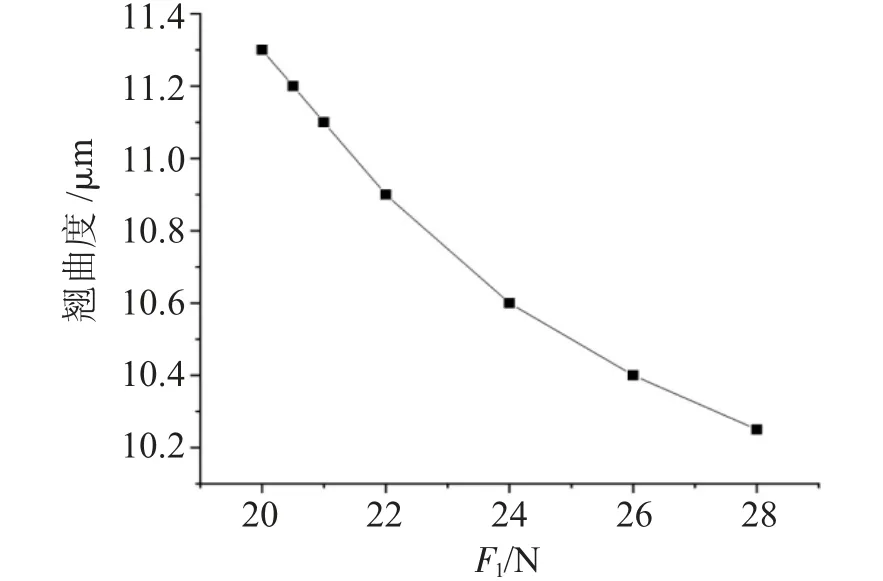
圖2 鋼絲張緊力對砷化鎵切片翹曲度的影響
從圖2中可以看出,隨著張緊力的增大,翹曲度逐漸減小。這是因為張緊力越大,鋼絲繃得越緊,鋼絲的弓角越小,切削能量損耗系數越小,進入切片內部熱量減小,而切片散熱能力大小基本相似,因此切片溫升有所減小,切片翹曲度減小。然而鋼絲張緊力過大時,鋼絲易達到抗拉強度導致拉斷,同時會降低導輪和過線輪的使用壽命,因此應該綜合考慮選擇基本滿足晶片幾何參數條件下的張緊力。
3.2 鋼絲速度對翹曲度影響
在鋼絲張緊力F1=20 N,進給速度vw=0.12~0.22 mm/min,鋼絲線徑d=0.12 mm時,通過改變式(8)中鋼絲速度vc,分析鋼絲速度與切片翹曲度之間關系,如圖3所示。
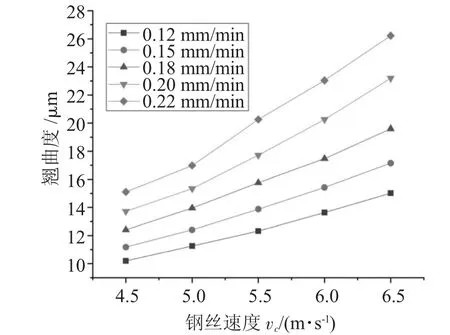
圖3 鋼絲速度對砷化鎵切片翹曲度的影響
圖3為分別在不同的進給速度下鋼絲速度對切片翹曲度影響。從圖3中可以看出,同一進給速度下,隨著鋼絲速度增大切片翹曲度逐漸增大。這是因為鋼絲速度越大,線鋸切割功率越大,線切阻力越大,切削產生熱量越多,而鋼絲弓角保持不變,即切削熱損耗系數不變,單位時間進入切片內熱量增多,切片散熱能力不變,切片翹曲度變大。
3.3 進給速度對翹曲度影響
在鋼絲張緊力F1=20 N,鋼絲速度vc=4.5~6.5 m/s,鋼絲線徑d=0.12 mm時,通過改變式(8)中晶棒進給速度vw,進一步分析進給速度對切片翹曲度的影響情況,結果如圖4所示。可以看出同一鋼絲速度下,隨著進給速度增大,切片翹曲度逐漸增大。這是因為隨著進給速度增大,單位時間內材料切除量增多,產生熱量增多,同時切削熱損耗系數也越大,單位時間進入切片內熱量越多,而切片散熱能力基本保持不變,切片翹曲度增大。比較圖3與圖4發現,相較于鋼絲速度變化,進給速度變化對切片翹曲度影響更明顯。
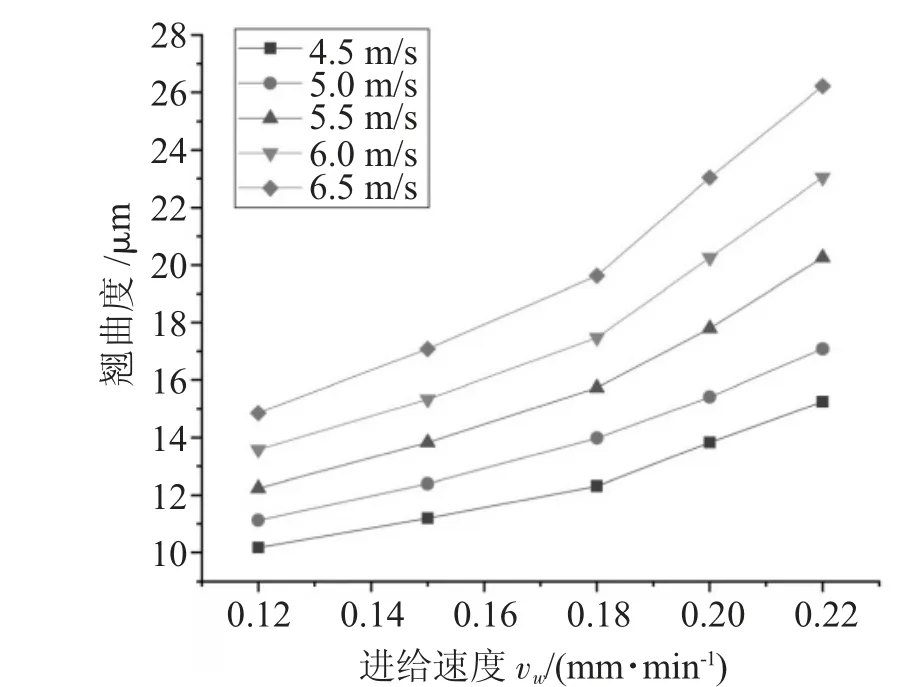
圖4 進給速度對砷化鎵切片翹曲度的影響
3.4 鋼絲線徑對翹曲度影響
在鋼絲張緊力F1=20 N,鋼絲速度vc=5 m/s,進給速度vw=0.15 mm/min時,通過改變鋼絲線徑d=0.12 mm,分析線徑與翹曲度關系,如圖5所示。
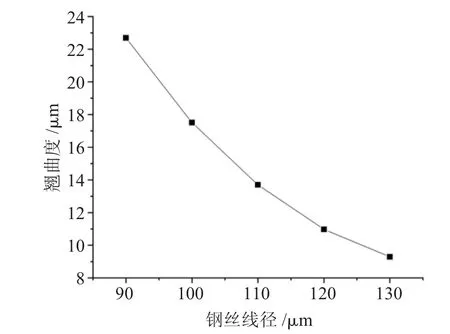
圖5 不同線徑對砷化鎵切片翹曲度的影響
由于砷化鎵晶棒價格昂貴,較小線徑可提高單位尺寸砷化鎵晶棒出片數,鋼絲線徑減小成為一種發展趨勢。鋼絲線徑對切片翹曲度影響在計算模型中主要通過改變切縫寬度d體現。從圖5可以看出:隨著鋼絲線徑減小,切片翹曲度逐漸增大,這是因為隨著鋼絲線徑減小,線切區域減小帶來切縫變窄,單位面積作用熱載荷增大,通過熱傳導進入切片熱量增多,而切片散熱能力減弱,升溫越高,因此不同線徑之間翹曲度相差明顯。但線徑過小,會導致線切過程中因偶發因素導致斷線的幾率升高,對于砷化鎵晶棒而言,由于砷化鎵材料硬度較小,斷線后重新布線續切也會導致切片表面產生線痕。因此在實際生產中,需要綜合考慮各方面因素,選擇最優的線徑。
4 結束語
本文建立了砷化鎵晶棒多線切割順序耦合熱應變分析有限元模型,以切片表面節點位移反映切片翹曲度。首先建立溫度場三維有限元模型,模擬切割過程溫度場分布;然后以溫度場結果為邊界條件,建立熱應變分析模型;按照不同的張緊力、進給速度、鋼線速度等工藝參數組合進行仿真模擬,計算出相應的翹曲度值,研究翹曲度與各工藝參數之間的關系。結果表明:多線切工藝參數主要通過影響切片散熱能力影響切片翹曲度。切片翹曲度隨著鋼絲速度和進給速度增大而增大,隨著鋼絲張緊力和線徑增大而減小,且相對于鋼絲速度進給速度變化對切片翹曲度影響更明顯。在實際生產中選擇工藝參數時,在設備允許的條件下應選擇較大的鋼線張緊力,在兼顧生產效率和成本的條件下,應選擇較小的鋼線速度、晶棒進給速度和鋼線線徑。

