結合GIS與FNN-SGD的雷波縣泥石流易發性評價

董艾嘉，鄔春學

（上海理工大學光電信息與計算機工程學院，上海 200093）

0 引言

雷波縣位于四川省西南部，地質災害對雷波縣可持續發展的制約日益顯著［1-2］。自然災害從本質上來說是多面性與不可預測的［3］，泥石流易發性分析是評估危害和風險的第一步，其顯示了一個地區發生泥石流的可能性與其地貌特征有關［4］。泥石流災害的發生會給當地居民帶來很大的安全隱患，因此對雷波縣泥石流易發性進行評價是非常必要的［5］。

泥石流易發性評價結果會影響對雷波縣泥石流易發地的預測，因此找出精度較高的模型是實現泥石流易發性評價的重要前提［6］。隨著GIS 技術的發展，傳統的多元統計方法可分為概率和確定性預測，已廣泛應用于災害預測與評估中［7］。隨著科技的進一步發展，機器學習技術在地質災害預測中也得到了廣泛應用，從神經網絡到前饋神經網絡（Feedforward Neural Network，FNN），由單層感知器到多層感知器，克服了感知器不能對線性不可分數據進行識別的弱點。文獻［8］通過神經網絡模型，可較好地處理區域內災害易發性與影響因子的非線性關系，對評價因子的權重計算更準確。邏輯回歸（Logistic Regression，LR）通過建立多元線性回歸方程，可明確表示因變量與一個或多個自變量之間的多元回歸關系，從而預測泥石流的易發地。文獻［9］采用邏輯回歸模型對干熱河谷區進行泥石流易發性評價，可為該地區泥石流預測和防治提供參考依據。隨機森林（Random Forest，RF）可處理具有高維特征的輸入樣本，且不需要降維，能夠評估各個評價因子在分類問題上的重要性。文獻［10］將隨機森林模型應用于泥石流敏感性分析，無需提前設置因子權重，即可對評價因子進行重要性分析，便于分析各評價因子對泥石流發育的影響。隨機梯度下降（Stochastic Gradient Descent，SGD）可將特征縮放及均值歸一化，以保證特征取值在合適的范圍內。文獻［11］采用隨機梯度下降法選取合適的學習速率，使得模型以較快速度收斂到最優解，因為每次選取一個樣本計算隨機梯度，從而大大減小了每次更新所用時間。

考慮到雷波縣泥石流樣本數量的有限性，雖然隨機過采樣通過簡單復制樣本的策略增加少數類樣本可實現樣本均衡，但是容易造成模型過擬合，從而導致模型學習到的信息過于特別而不夠泛化，因此本文采用改進的隨機過采樣算法（Synthetic Minority Oversampling Technique，SMOTE）。泥石流災害點共有39 個，潛在泥石流災害點有114 個，將其視為正樣本（153 個），通過合成少數類過采樣技術，將少數類樣本合成新樣本添加到數據集中。最終使得泥石流負樣本與正樣本數量相同，得到新的均衡的負樣本（153 個），從而使正負樣本比例均衡。隨機選擇70%的正樣本（153個）和負樣本（153個）作為訓練樣本，剩余30%的數據作為測試樣本。

評價因子的選擇也是保證評價模型準確、合理的關鍵前提。在分析雷波縣地質條件和社會活動的基礎上，結合雷波縣地質災害分布情況，利用研究區域資料、地理資源網站、遙感影像提取了14 個對泥石流有影響的因子，每個評價因子相互獨立，并分析各個因子之間的聯系，采用頻率比（Frequency Ratio，FR）對評價因子進行輔助分析［12］。其中10 個因子影響顯著，包括降水量、高程、坡度、坡向、巖性、剖面曲率、歸一化植被指數、到河流距離、土地利用情況、到公路距離與雷波縣泥石流發生之間存在明顯關聯，可作為雷波縣泥石流易發性評價體系中的評價因子。

泥石流易發性分布圖可為地質災害的防治管理提供依據［13］。利用FNN-SGD 模型對雷波縣泥石流的易發性進行評價，并與前饋神經網絡、邏輯回歸、隨機森林3 種模型的結果進行分析比較，將雷波縣泥石流易發性劃分為5 個等級，利用GIS 繪制易發性分布圖，并使用ROC 曲線驗證模型的準確率，得出前饋神經網絡、邏輯回歸、隨機森林、FNN-SGD 的準確率分別為97.6%、93.1%、95.4%、98%，預測成功率分別為96.3%、90.9%、93.6%、97.1%。準確率與預測成功率之間的差值可體現模型的穩定性，按照由大到小排序分別為邏輯回歸（2.2%）、隨機森林（1.8%）、前饋神經網絡（1.3%）、FNN-SGD（0.9%）。由此可知，FNN-SGD模型比較穩定、可靠，具有良好的泛化能力。

本文在上述研究基礎上，創新地提出一種前饋神經網絡結合隨機梯度下降（Feedforward Neural Network and Stochastic Gradient Descent，FNN-SGD）模型，并與前人研究的單模型進行比較，驗證該模型的準確率和穩定性。結果表明，前饋神經網絡相比隨機森林對于評價因子權重的計算更為準確；邏輯回歸模型在建模過程中受到的主觀干擾較大；FNN-SGD 模型相比其他模型的準確率更高、效果更好，可提高雷波縣泥石流易發性區域劃定精度，更適用于雷波縣泥石流易發性評價。

1 相關技術

1.1 優化隨機過采樣

對于特定的研究區域，泥石流作用下的面積總是小于總面積，使得樣本數據不平衡。對于某一不平衡數據集，分類越不平衡，準確度越低。當數據相對平衡時，分類效果最好。數據平衡是通過改變數據分布來實現的，其中最常見的策略是過度采樣和采樣不足［14］。

本研究的主要目的是預測雷波縣的泥石流易發性分布。由于雷波縣的泥石流樣本數量有限，而且不同研究區域引發泥石流的外部因素與地形條件存在較大差異，因此采用研究區域以外的泥石流災害樣本數據進行平衡的方法是不可取的［15］。

在實際應用中，泥石流數據很難滿足多元正態分布及變量之間的相互獨立。本文將泥石流災害點視為正樣本，非泥石流災害點視為負樣本，若正負樣本不均衡將會對算法的學習過程造成很大干擾，較少的正樣本有可能會被預測為數量較多的負樣本。為解決正負樣本不平衡的問題，本研究采用SMOTE 算法，其是一種優化的隨機過采樣算法。泥石流災害點共有39 個，潛在泥石流災害點有114個，將其視為正樣本（153 個），通過合成少數類過采樣技術，將少數類樣本合成新樣本添加到數據集中。

隨機選取一個少數類樣本，以歐式距離為標準計算出其到所有樣本的距離，得出k 近鄰。根據樣本不均衡比例，設定一個采樣比例來確定采樣倍數n。對任意一個少數類樣本x，從其k 近鄰中隨機選若干樣本。對于任意一個隨機選出的近鄰，挑選［0，1］之間的隨機數乘以隨機近鄰與x特征向量的差，然后再加x，如公式：

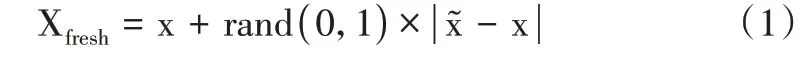
最終，使得泥石流負樣本與正樣本數量相同，得到新的均衡的負樣本（153個），使得正負樣本比例均衡。

泥石流易發性預測統計模型是通過訓練樣本建立自變量與因變量之間的關系，然后通過檢驗樣本驗證其關系。因此，機器學習模型需要用兩個單獨的數據樣本進行訓練與檢驗。為識別與區分訓練集和驗證集，可使用不同策略，采用最適用的一次性隨機選擇方法［16］。本文研究區域分為306 個單元，其中39 個單位是歷史災難點，114 個單位是潛在的泥石流災難點，將其視為正樣本，剩余的153個單元視為負樣本。在構建模型前，隨機選擇70%的正樣本（153 個）和負樣本（153 個）作為訓練樣本，剩余30%的數據作為測試樣本。

1.2 前饋神經網絡

前饋神經網絡（Feedforward Neural Network，FNN）的研究從20 世紀60 年代開始，其是目前應用最廣泛、發展最迅速的神經網絡之一［17］。前饋神經網絡采用一種單向多層結構，其中每一層包含若干個神經元［18］。在神經網絡中，各神經元可接收前一層神經元的信號，并將輸出結果輸入到下一層。本研究是將降雨量、高程、坡度、坡向、巖性、剖面曲率、NDVI、到河流距離、土地利用情況、到公路距離共10 個特征量作為輸入層，兩層隱藏層先計算輸入層的特征量，再進行數據分析，將是否發生泥石流作為輸出結果，最后轉換成外界能夠識別的信息。從評價因子作為輸入層到是否發生泥石流作為輸出層單向傳播，多層前饋神經網絡結構如圖1所示。

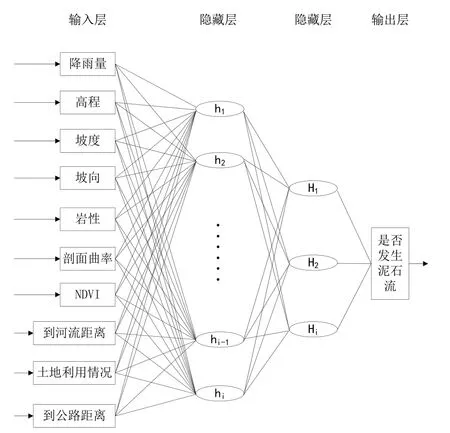
Fig.1 Structure of feedforward neural network圖1 多層前饋神經網絡結構

在多層前饋神經網絡中，每一層相當于一個單層的前饋神經網絡，采用生長法更符合認識事物的規律。輸入與輸出之間的變換關系為：

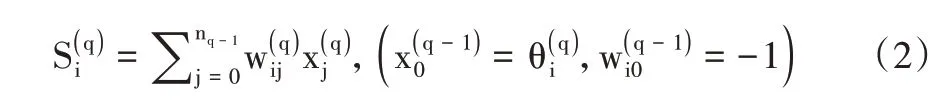
式中，對于第q 層，x 是輸入的特征向量，即評價因子；wij是xi到的連接權是按照不同特征的分類結果：

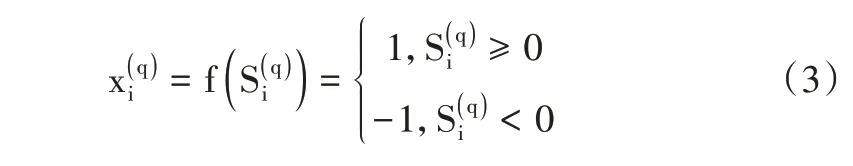
式中，i=1，2，…，nq；j=1，2，…，nq-1；q=1，2，…，Q。對于第q 層，會形成一個nq-1維的超平面。函數表示對于輸入x 的分類結果，類別1 表示正例，類別0 表示負例。

1.3 邏輯回歸

邏輯回歸模型（Logistic Regression，LR）可以明確因變量與一個或多個自變量之間的多元回歸關系。將泥石流事件認為是二分類問題，不直接預測標簽是0 或1 分別表示泥石流事件的負或正，而是預測輸出數值是0 或1 的概率，因此邏輯回歸模型根據所選的因變量計算目標事件的發生概率。

式中，P 表示泥石流事件發生的概率，Y 表示泥石流事件，由以下公式進行計算：

式中，θ0為方程的常數值或截距，θ1，θ2，…，θn為最佳參數，X0，X1，…，Xn 為訓練數據的向量。本研究的預測函數為：

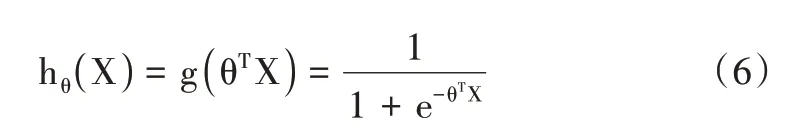
式中，hθ(X)表示對于X 的分類結果，θT表示訓練過的一組權值，X 表示需要預測的向量。分類結果為類別1（事件正例）和類別0（事件負例）的概率分別為：

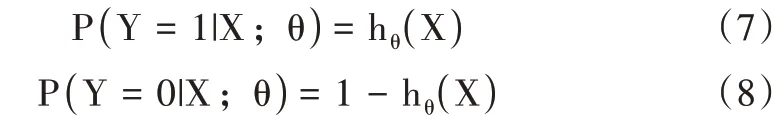
1.4 隨機森林

隨機森林（Random Forest，RF）是多個決策樹的組合，一般決策樹的數量越多，泛化結果越好。多個決策樹對數據進行分類時，可給出自變量的相對重要性占比，評價自變量對泥石流造成的影響。針對泥石流易發性評價的研究采用一種基于統計學習理論的機器學習算法，通過集成多棵決策樹，然后采用投票方式選出分類結果。在數據預處理階段，對于不平衡的分類數據集，隨機森林模型可平衡誤差；在評價指標選取階段，隨機森林模型處理多維度和大量數據集的速度快，比決策樹的非線性擬合能力強；在易發性評價階段，隨機森林模型可分析出評價指標的重要性，模型的可解釋性強。

在本研究中，樹的數量（k）和用于分割節點的預測變量數量（m）是形成隨機森林所需定義的參數。為保證算法的收斂性和良好的預測結果，采用CART 決策樹通過基尼指數進行特征選擇，使用基尼指數最小的特征對子節點進行劃分。將樹的數量k固定為500，選取預測變量m 為3。

假設有M 個特征X1，X2，…，Xm，基尼指數的公式為：

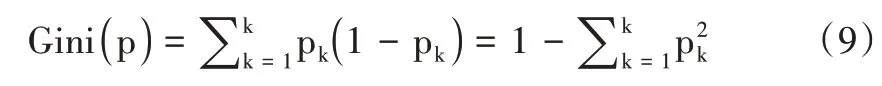
式中，k表示類別數量，pk表示類別k所占比例。

對于處理好的數據集，采用70%的樣本構建隨機森林模型進行計算，剩余30%的樣本對訓練集進行驗證。從訓練數據N 中有放回地隨機抽取k個樣本，然后通過n 次隨機采樣得到n 個訓練集。對于n 個訓練集，分別訓練n 個決策樹模型。根據訓練數據的特征M，隨機選取m 個特征作為該節點的分裂特征集。

1.5 FNN-SGD

前饋神經網絡結合隨機梯度下降（Feedforward Neural Network and Stochastic Gradient Descent，FNN-SGD）模型是一個有單個輸出節點的前饋神經網絡，當此節點輸出越接近1（泥石流發生的正例），越可能符合泥石流發生的條件，越接近0（泥石流發生的負例）則越不可能發生泥石流。本研究通過交叉熵判斷兩個概率分布之間的距離。設p 為泥石流發生的概率，q為泥石流未發生的概率：

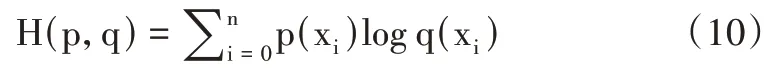
H(p，q)表示泥石流發生的正、負概率分布之間的距離。前饋神經網絡的輸出不一定是一個概率分布，雷波縣泥石流事件總數是有限的，概率分布函數需滿足：

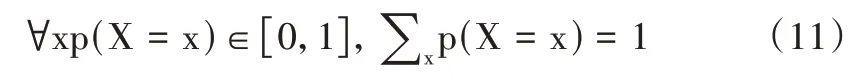
式中，x 表示任意事件，任意事件的發生概率都在［0，1］范圍內。通過上述方式將非線性單元進行映射，接下來對樣本進行分類，然后識別出相應類別。隨機梯度下降可用于求解非線性的最小二乘問題，在前饋神經網絡求解過程中，沿梯度下降方向求解極小值，沿梯度上升方向求解極大值。

在機器學習中，為擬合輸入樣本，建立了目標函數h(θ)。目標函數計算公式如下：

式中，j 表示參數個數，為評估模型擬合質量，用損失函數度量擬合程度。l(θ)損失函數計算公式如下：

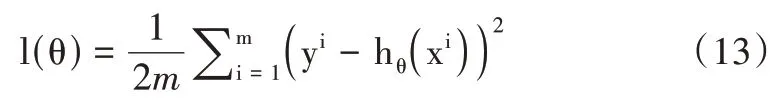
式中，m表示總迭代次數，這里的1/2 是為了方便求導，l(θ)函數的收斂曲線表示模型擬合程度，對應的模型參數為最優參數。θ計算公式如下：

式中，θ表示初始化參數，?θ表示梯度，η 表示下降系數，即梯度下降的步長。首先計算出損失函數的梯度，然后沿梯度方向使損失值逐漸減小，得出最小的函數損失值，從而得到最優解。

雖然機器學習模型如前饋神經網絡、邏輯回歸、隨機森林等單個的機器學習模型在地質災害評價體系中應用廣泛，但是基于多模型組合的應用較少。本文將FNNSGD 應用于泥石流易發性評價中，并與單模型進行對比分析，以驗證該模型應用于泥石流易發性評價中的準確率和穩定性。

1.6 模型評估

采用頻率比法（Frequency Ratio，FR）定量分析泥石流發生的影響因素與泥石流發生的關系。本文的FR 是在分析影響因子和泥石流災害點的基礎上，計算影響因子與泥石流災害點之間的關系。FR 值計算公式如下：

式中，下標i 為所考慮的每個變量的第i 類，Di為控制因子第i 類所包含的泥石流災害點數，D 為研究區域泥石流災害點總數，Ui為控制因子第i 類所包含的泥石流災害單元總數，U 為研究區域單元總數。當FR 大于1 時，表示該評價因子與事件的相關性更強；反之，表示相關性更弱。因此，以頻率比為參考，驗證模型對評價因子的選擇與評價是否合理。

如果沒有適當的評估或驗證，模型及獲得地圖的科學價值較低。因此，對模型結果進行評價與驗證是泥石流易發性評價不可或缺的任務。近年來，人們采用多種方法來評估模型的不確定性和預測能力，如準確率曲線和預測成功率曲線、列聯表、ROC（Receiver Operating Characteristic）曲線和AUC（Area Under Curve）曲線等。AUC 是衡量地質敏感性評價效果的標準指標。本研究采用FR 對評價因子進行分析，通過ROC 曲線和AUC 曲線對FNN、LR、RF、FNN-SGD 建立的模型進行評價與驗證（見圖2）。

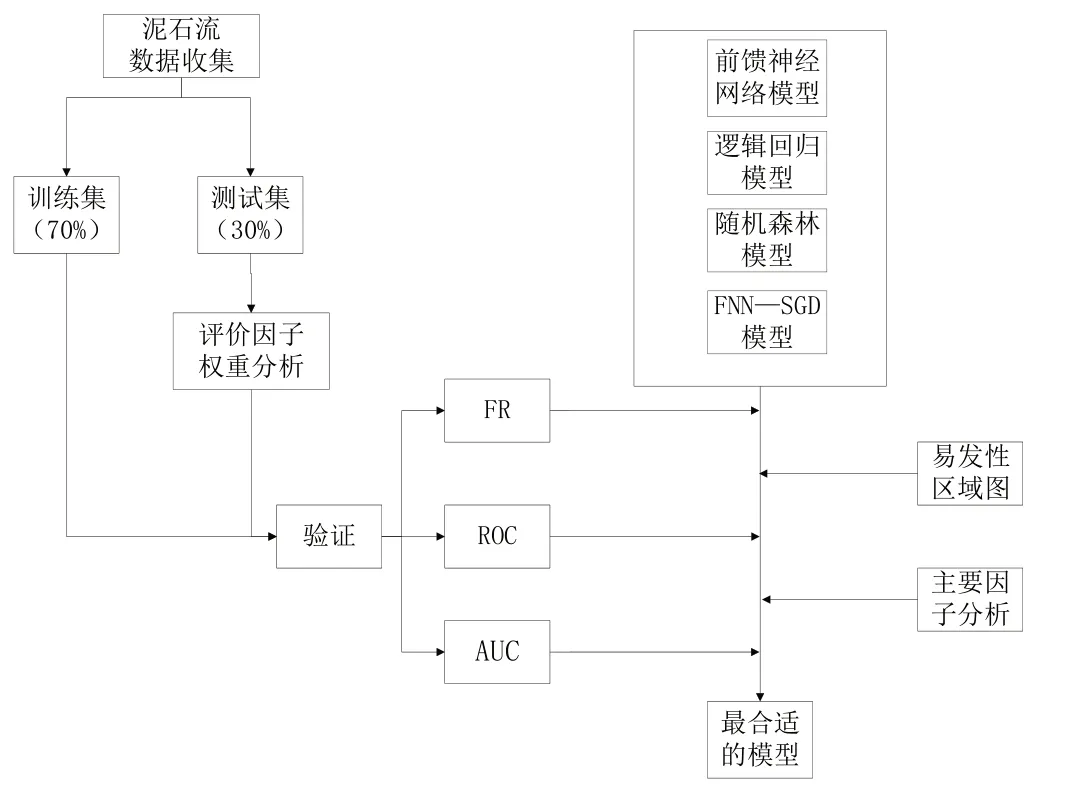
Fig.2 Research flow圖2 研究流程

2 實驗與分析

2.1 研究區域

研究區域雷波縣位于四川省西南邊緣、涼山彝族自治州東部、金沙江下游北岸，是歷史上泥石流地質災害較為頻繁的地區。其地處北緯27°49'-28°36'，東經103°10'-52'之間，面積2 932km2；海拔高度為380～4076m，相對差近3 700m；地質構造復雜，地貌種類多，有大江大湖、高山峽谷、瀑布溶洞、森林草原等；屬于亞熱帶山地立體氣候，年均降雨量900ms，屬于多雨地區，日照1 250h，氣溫13℃，常年空氣濕度保持在70%左右。

雷波縣曾發生過多次泥石流，分別在2002 年8 月9 日（碉樓溝）、2007 年5 月20 日（莫紅溝）、2015 年5 月7 日（部分鄉鎮），給當地造成了巨大的經濟損失和人員傷亡。因此，能否快速、有效地根據泥石流發生的歷史數據，分析與判斷泥石流的易發生區域，對預防泥石流地質災害、減少當地人民的生命和財產損失具有極其重要的意義。本文針對此問題進行研究，基于GIS 和FNN-SGD 對泥石流易發性區域進行分析，并給出對泥石流易發性區域情況的分析和判斷。

雷波縣以山地地貌為主，構造活動強烈，地質環境復雜。雷波縣現存由國土資源部門負責防治的地質災害隱患點150 處，其中滑坡66 處，崩塌34 處，泥石流35 處，不穩定斜坡15 處，共威脅4 121 戶19 393 人。最后，確定本研究所選的區域位置，如圖3 所示（彩圖掃OSID 碼可見，下同）。

一份完整、準確的泥石流清單地圖對于模型訓練與驗證是必不可少的，因為建模方法是基于過去和現在對未來的假設。在本研究中，數據分別來自中國氣象科學數據共享服務網的全國降雨量數據、地理空間數據云的DEM 數字高程數據（GDEMV2 30M 分辨率數字高程數據）、LANDSAT 系列數據（Landsat 8 OLI_TIRS 衛星數字產品）、Globe-Land30 的2020 版30m 全球地表覆蓋數據與OpenStreetMap的路網數據。評價因子數據來源如表1所示。

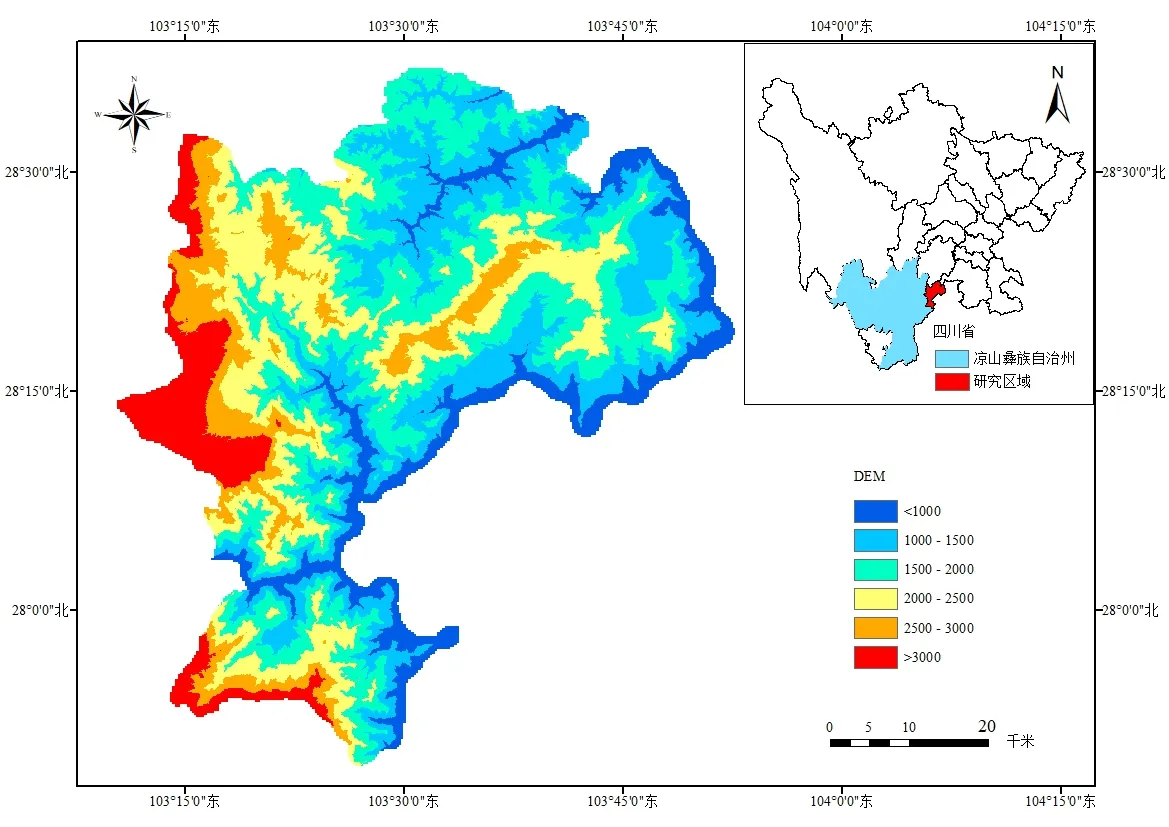
Fig.3 Location of the study area in Sichuan圖3 研究區域在中國四川省的位置

選取真正影響模型結果的評價因子作為輸入參數是開展泥石流易發性評價的關鍵。地形、地質和氣候因素對泥石流的分布與活動起著至關重要的作用。因此，數據的可用性、可靠性和實用性也被考慮在內。本研究的控制因素包括：①降雨條件；②地形條件（高程、坡度、坡向、等高線、剖面曲率）；③地質條件（巖性）；④植被條件；⑤河流分布（河網密度、到河流距離）；⑥人類活動條件（土地利用情況、路網密度、到公路距離）。

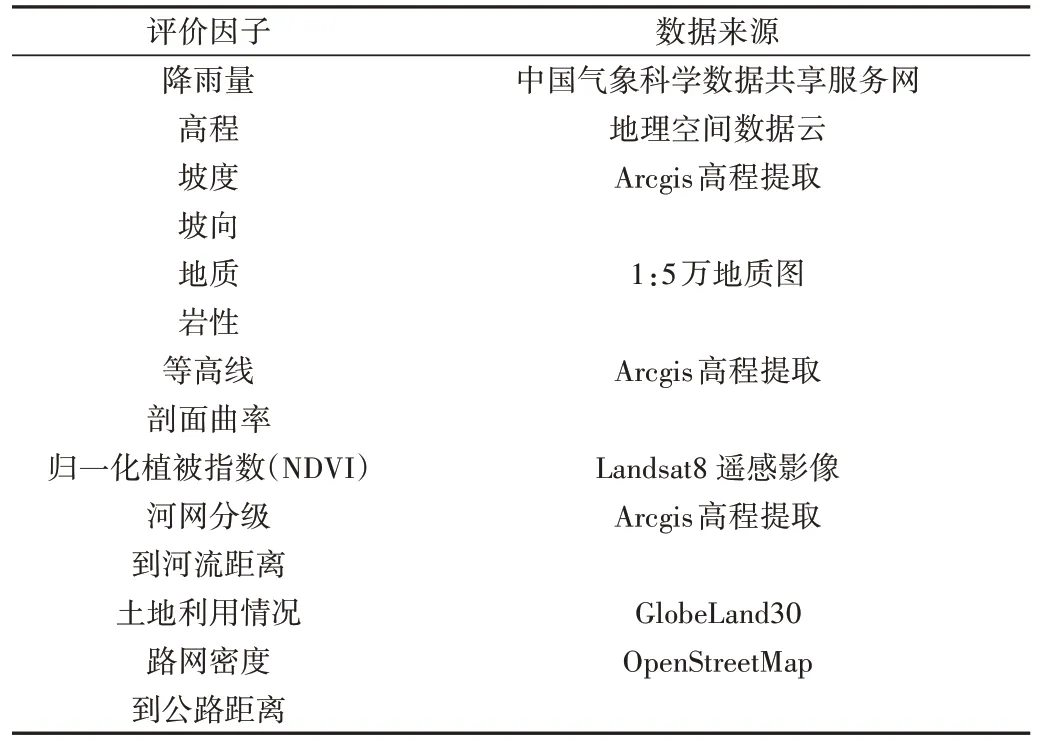
Table1 Data sources of evaluation factors表1 評價因子數據來源

按照雷波縣泥石流災害分布特點將每個評價因子的子類劃分為4～9 類，使每個間隔單元盡可能服從正態分布。得到該研究區域的降雨量、高程、坡度、坡向、剖面曲率、等高線、地質、巖性、NDVI、河網分級、到河流距離、土地利用情況、路網密度、到公路距離共14 個評價因子圖（見圖4）。

2.2 降雨條件

四川省涼山彝族自治州雷波縣流域內的季節性降雨引起一段時間內水位上漲，有可能引起泥石流。本研究將雷波縣2009-2019 年6-9 月降雨量（累計）用自然間斷點法分 為5 類：601～640mm，640～666mm，666～688mm，688～710mm，710～743mm，如圖4（a）所示。

降雨是誘發泥石流災害最重要的外部因素之一，可能會催化邊坡失穩。以研究區域雷波縣（站點編號：56 485，位置：28.27N、103.58E，海拔：1 255.8m）的逐月、逐日降雨量數據為參考，本研究選取2009-2019 年的月平均降雨量作為災害爆發的誘導因子，如圖5所示。

2.3 地形條件

與地貌相關的因子來自于數字高程模型（Digital Elevation Model，DEM），從地理空間數據云獲得30m 分辨率的DEM，可用ArcGIS 中的Data Management Tools、Spatial Analyst Tools、3D Analyst Tools 等工具得出坡度、坡向等相關信息。

海拔是另一個常用的調節因子，其不僅影響降雨和植被狀況，而且有助于泥石流的發生。利用ArcGIS 中的工具，首先將DEM 數據進行拼接，然后按照涼山彝族自治州雷波縣的行政區提取拼接的DEM 數據，最后通過投影柵格得到高程。本研究區域的高程以500m 為間隔，分為6類：0～400m，400～600m，600～800m，800～1 000m，1 000～1 500m，>1 500m，如圖4（b）所示。

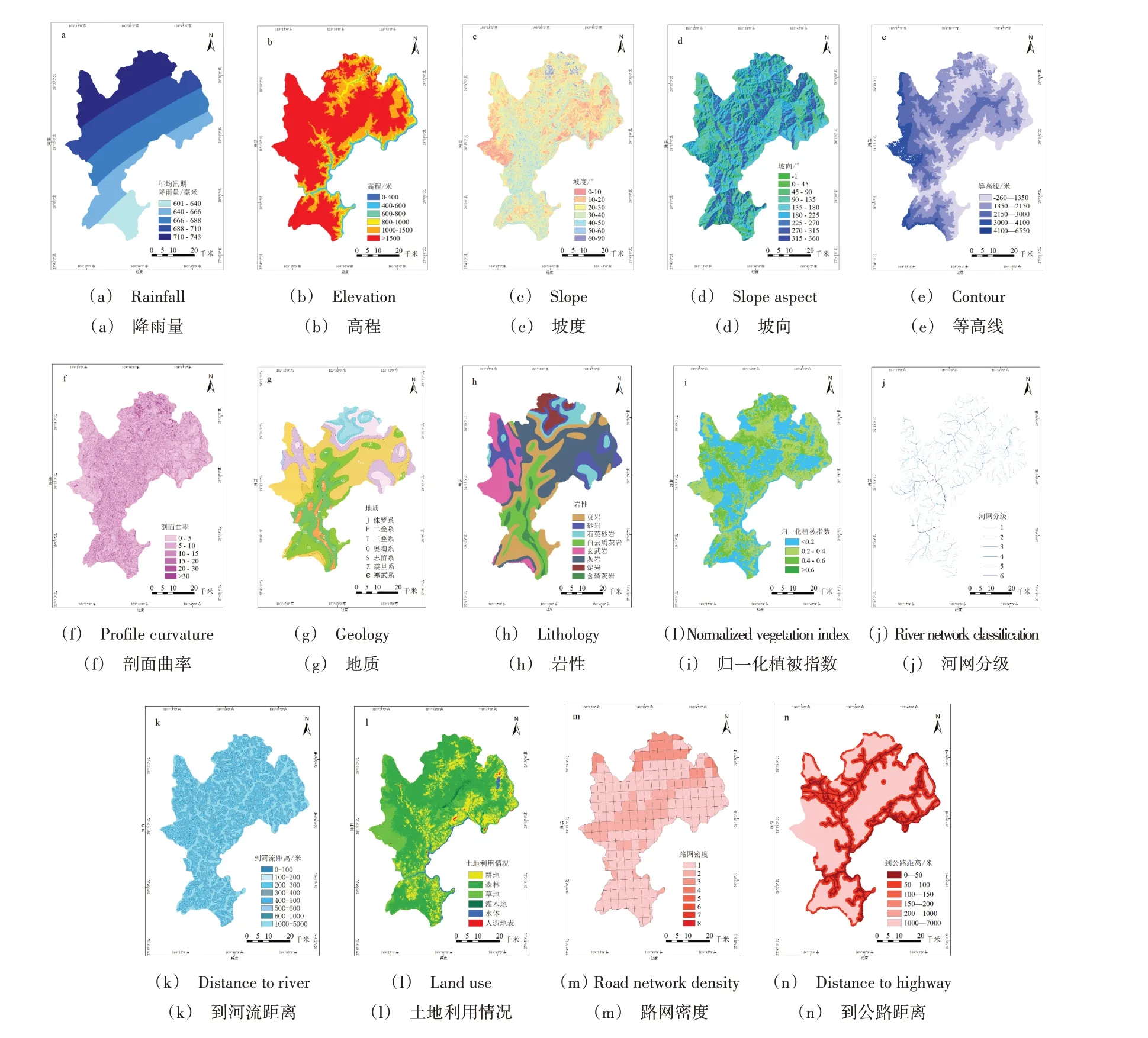
Fig.4 Classification map of evaluation factors in Leibo County圖4 雷波縣評價因子分類圖

Fig.5 Average monthly precipitation（cumulative）in Leibo county from 2009 to 2019圖5 2009-2019年雷波縣每月降水量（累計）平均值

坡度通常被認為是影響邊坡穩定性最重要的因素之一，其不僅能引起邊坡重力變形，而且能控制應力分布。利用ArcGIS 中的工具從上述高程數據中獲取坡度，本研究區域的坡度圖分為7 類：0°～10°，10°～20°，20°～30°，30°～40°，40°～50°，50°～60°，60°～90°。坡度圖顯示斜角在0°～90°之間，以10°為間隔，如圖4（c）所示。

坡向表示單元格所在位置面對的指南針方向，此因素可通過影響太陽輻射暴露，從而調節斜坡上的土地覆蓋和水分蒸發情況。利用ArcGIS 中的工具從上述高程數據中得到坡向，本研究區域將坡向數據分為9 個基本方向：-1，0°～45°，45°～90°，90°～135°，135°～180°，180°～225°，225°～270°，270°～315°，315°～360°，以45°為間隔，其中-1 是當單元格沒有下坡方向（即平坦區域）時給出的值，如圖4（d）所示。

等高線是地形圖上高程相等且相鄰的各點所連成的閉合曲線。等高線每上升1 000m，溫度降低6℃。一般來說，等高線稀疏，坡度平緩；等高線密集，坡度陡峭。本研究用自然間斷點的分級方法將等高線劃分為5 類：-260～1 350m，1 350～2 150m，2 150～3 000m，3 000～4 100m，4 100～6 550m，如圖4（e）所示。

剖面曲率代表地形表面的起伏程度，對泥石流的形成有一定輔助作用。剖面曲率值＞0時，地形表面會朝下凹；相反，曲率值＜0時地形會朝上凸；曲率值為0 時，地面為水平。本研究將剖面曲率劃分為6 類：0～5，5～10，10～15，15～20，20～30，>30，如圖4（f）所示。

2.4 地質條件

雷波縣位于“川滇南北向構造帶”與“盆地新華夏系沉降帶”交接地帶，縣域西部以南北向構造帶為主，中部和東部則以北東向構造帶為主，東部有少量南北向構造。本研究將地質情況分為7 類，分別為：侏羅系、二疊系、三疊系、奧陶系、志留系、震旦系、寒武系，如圖4（g）所示。

泥石流在不同巖性中的發育程度不同，當巖石層遭到破壞，碎屑為泥石流的形成提供了充足的物質。雷波縣的巖性可分為8 類，分別為：白云巖、泥巖、砂巖、石英砂、頁巖、灰巖、含磷巖、玄武巖。雷波縣巖性分布圖如圖5（h）所示。

2.5 植被條件

從地理空間數據云的Landsat 8 系列獲取植被覆蓋圖像，接下來利用ArcGIS 提取雷波縣行政界限的圖像，再使用柵格計算器計算歸一化植被指數。歸一化植被指數（NDVI）計算公式如下：

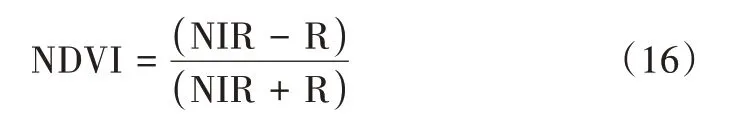
式中，NIR、R 分別為近紅外波段和紅外波段處的反射率值。由此公式計算出本研究區域的歸一化植被指數（NDVI），再將植被覆蓋度的范圍設置為0～1，共分為4 類：0～0.2、0.2～0.4、0.4～0.6、0.6～1，如圖4（i）所示。

2.6 河網條件

河網是滑坡的重要制約因素，其可以通過切割、軟化、侵蝕等方式長期改變河岸邊坡的地質條件。根據上述獲取的DEM 數據，利用ArcGIS 中的工具，首先填充DEM 洼地，然后通過水文分析得出本研究區域的河流流向、流量，可看出水流脈絡，接下來利用柵格計算器，使用con 函數得出對河網的分析結果，可看到精細的河網結構，再使用Strahler方法將不同等級的溪流用不同顏色表示出來，最后將柵格河網矢量化。本研究將河流密度劃分為6 個等級，如圖4（j）所示。

針對到河流距離，本文使用歐氏距離進行分析，將到河流距離根據泥石流災害分布特點重新劃分為8 類：0～100m，100～200m，200～300m，300～400m，400～500m，500～600m，600～1 000m，1 000～5 000m，如圖4（k）所示。

2.7 人類活動條件

從變化的地質條件來看，土地利用情況也可被認為是人類活動的指標，如耕地、森林和人造地表等。從Globe-Land30 2020 版16m 分辨率高分一號（GF-1）多光譜影像中獲取涼山彝族自治州雷波縣的地表覆蓋數據，本研究利用ArcGIS 中的工具按照行政邊界提取雷波縣的地表數據后，從這些特征中提取屬性信息，包括耕地、森林、草地、灌木地、水體與人造地表。本研究區域的土地利用情況分為6類，如圖4（l）所示。

公路建設在山區發展過程中起著重要作用，但開挖活動往往會影響邊坡的穩定性。因此，路網密度可作為另一個外部變量。從OpenStreetMap 中獲取涼山彝族自治州雷波縣的路網數據，利用ArcGIS 中的工具創建漁網，再將漁網與路網相交，通過柵格計算器計算路網密度，對道路（鐵路、公路、水路）長度總和與每個單元格面積之比進行計算，生成地形圖（單位：km/km2）。本研究將路網密度分為8類，如圖4（m）所示。

一般來說，泥石流災害點與主干道路越接近，泥石流發生后路人面臨的危險性越大?？紤]到劃分緩沖距離的合理性，本研究將到公路距離分為6 類：0～50m，50～100m，100～150m，150～200m，200～1 000m，1 000～7 000m，如圖4（n）所示。

3 實驗結果及分析

3.1 評價因子分析

與頻率比法（Frequency Ratio，FR）相比，4 種模型對評價因子的分析存在顯著差異?；陬l率比法，可更詳細地探索各評價因子與泥石流之間的潛在關系。雷波縣泥石流易發性頻率比值如表2所示。

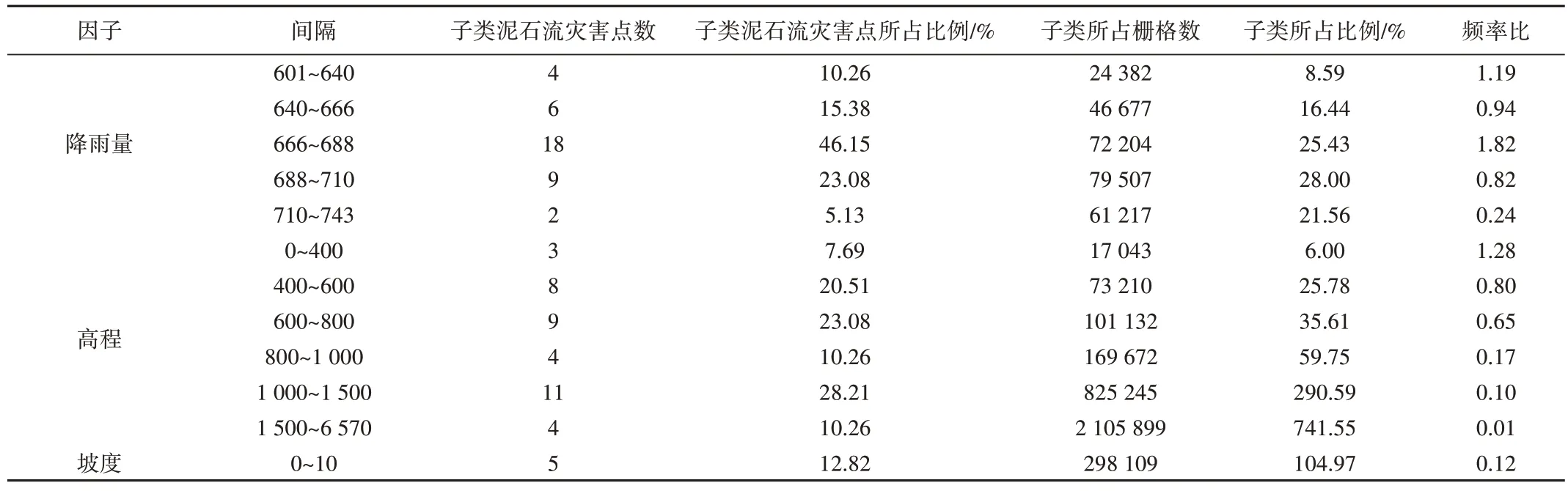
Table 2 Frequency vatio of debris flow susceptibility表2 泥石流易發性頻率比值

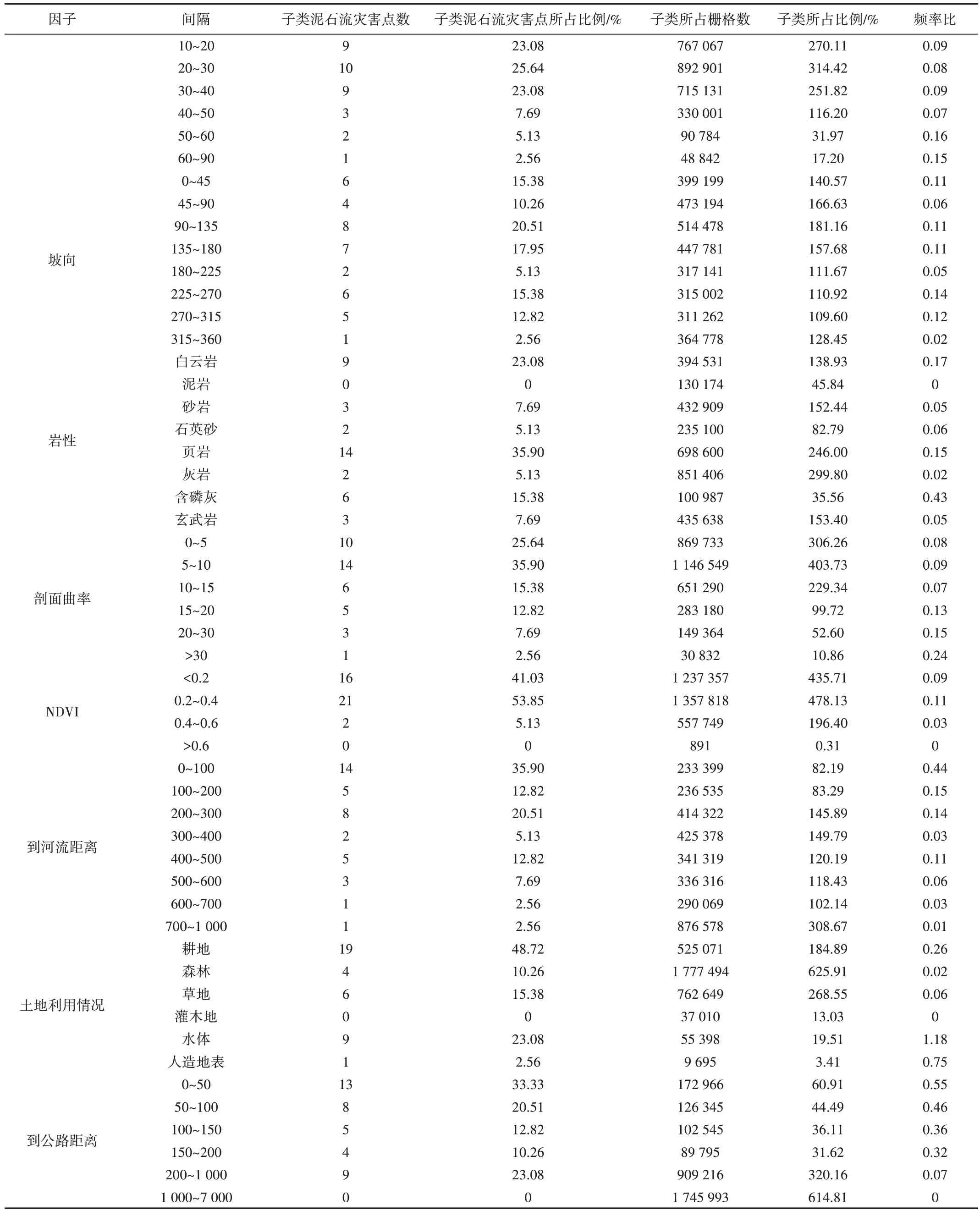
續表

由表2 可知，降雨量、高程和土地利用情況對泥石流災害的敏感度更高。以降雨量為例，降雨量的子類666～688mm 相較于降雨量的其他子類對泥石流災害更敏感。通過上述例子依次判斷剩余評價因子的子類敏感度，得到高程的子類0～400m、坡度的子類50°～60°、坡向的子類225°～270°、剖面曲率的子類>30、巖性的子類含磷灰、歸一化植被指數的子類0.2～0.4、到河流距離的子類0～100m、土地利用情況的子類水體、到公路距離的子類0～50m 對泥石流災害更敏感。

3.2 模型結果

本研究將四川省涼山彝族自治州雷波縣的泥石流易發性分為5 類：極低易發性區域、低易發性區域、中易發性區域、高易發性區域、極高易發性區域，得到雷波縣的泥石流易發性分布圖，如圖6所示。

Fig.6 Distribution map of debris flow susceptibility in Leibo county圖6 雷波縣泥石流易發性分布圖

3.2.1 前饋神經網絡

前饋神經網絡模型將10 個評價因子作為輸入進行學習與訓練得出訓練結果，再利用ArcGIS 軟件得到泥石流地質災害易發性分布圖（見圖6（a））。根據自然間斷點方法將易發性評價結果分為：極高、高、中、低、極低，面積占比分別為：9.8%、15.42%、21.79%、26.49%、26.5%，各分區所對應的災害點數量分別為：18、12、8、1、0，位于高易發區域及以上的災害點數量占總災害點數量的76.92%。

前饋神經網絡得到評價因子相對重要性占比如圖7所示，分析結果表明：降雨量、到公路距離、高程是影響泥石流災害形成最重要的3 個因子，占全部因子重要性的63%；巖性、土地利用情況、坡度、剖面曲率也對泥石流災害的形成影響較大；坡向、NDVI、到河流距離對泥石流災害的形成影響較小，重要性僅占9%。

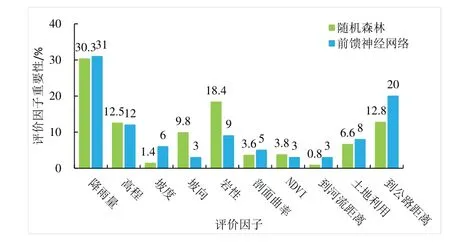
Fig.7 Relative importance ratio of evaluation factors圖7 評價因子相對重要性占比

3.2.2 邏輯回歸

邏輯回歸模型采用主效應方法對10 個評價因子進行學習與訓練，再利用ArcGIS 軟件得到泥石流地質災害易發性分布圖（見圖6（b））。根據自然間斷點方法將易發性評價結果分為：極高、高、中、低、極低，面積占比分別為：5.8%、14.23%、17.73%、23.99%、38.25%，各分區所對應的災害點數量分別為：10、14、4、8、3，位于高易發區域及以上的災害點數量占總災害點數量的61.54%。

邏輯回歸模型因其具有擬合模型的簡單性和擬合系數的可解釋性而被廣泛應用于各個領域，并被多次應用于泥石流易發性評價。根據模型中系數的正負符號，可直接判斷各自變量與因變量之間的關系，廣義線性模型系數也可用來評估評價因子的相對重要性。然而，邏輯回歸模型一般采用逐步回歸的方法對變量進行過濾，只留下少數統計上顯著的變量，這會導致對默認值有顯著影響的部分變量信息丟失。泥石流易發性評價過程涉及多個評價因子，邏輯回歸模型無法自主克服自變量之間的多重共線性對結果的影響。因此，該模型難以很好地分析泥石流的誘發因子，有時甚至會得出與以往經驗相反的結論。

3.2.3 隨機森林

隨機森林模型通過對數據的學習與訓練，得出了10個評價因子的重要性占比，再利用ArcGIS 軟件得到泥石流地質災害易發性分布圖（見圖6（c））。根據自然間斷點方法將易發性評價結果分為：極高、高、中、低、極低，面積占比分別為：6.91%、11.14%、17.43%、24.23%、40.3%，各分區所對應的災害點數量分別為：14、12、10、3、0，位于高易發區域及以上的災害點數量占總災害點數量的66.67%。

隨機森林得到評價因子相對重要性占比如圖7 所示，分析結果表明：降雨量、巖性、到公路距離、高程是影響泥石流災害形成最重要的4 個因子，占全部因子重要性的73.94%；土地利用情況、坡向也對泥石流災害的形成影響較大；坡度、剖面曲率、NDVI、到河流距離對泥石流災害的形成影響較小，重要性僅占9.61%。

隨機森林模型具有處理高維、小樣本和不平衡數據的能力，對模型依賴性沒有預先的假設，并且可以處理分類數據和連續數據。隨機森林模型的應用較好地保留了原始的控制信息，這些評價因子有助于更好地了解地質災害。所得結果的值越大，對泥石流發生的貢獻越大。然而，其結果并不像邏輯回歸模型那樣積極或消極。本文僅對每個評價因子的重要性進行排序，即每個因子默認都會促進泥石流的發生，但其效果是不同的。

3.2.4 FNN-SGD

FNN-SGD 模型首先通過前饋神經網絡模型訓練樣本，然后計算出損失函數的最小值，再通過隨機梯度下降的方向讓損失值逐步減小，從而得到最優解。利用ArcGIS軟件得到泥石流地質災害易發性分布圖（見圖6（d）），根據自然間斷點方法將易發性評價結果分為：極高、高、中、低、極低，面積占比分別為：9.19%、18.16%、25.18%、29.49%、17.98%，各分區所對應的災害點數量分別為：23、9、6、1、0，位于高易發區域及以上的災害點數量占總災害點數量的 82.05 %。

FNN-SGD 模型利用最初的數據集進行訓練，作為FNN 模型的第一層學習器，將FNN 模型輸出的結果作為特征帶入SGD 模型中進行二次學習，最后輸出結果。通過對多個模型的輸出結果進行泛化，可提升泥石流易發性預測精度。

在FNN-SGD 模型構建的易發性分區中，高和極高易發性區域主要分布于雷波縣東南部，中易發性區域分布于雷波縣西南部，低和極低易發性區域分布于雷波縣西北部和東北部。

本文將四川省涼山彝族自治州雷波縣的泥石流易發性分為5 類：極高、高、中、低、極低，通過4 個模型預測5 類易發性區域面積占雷波縣總面積的比值，以及各區域泥石流災害點分布情況，分別如表3、表4所示。

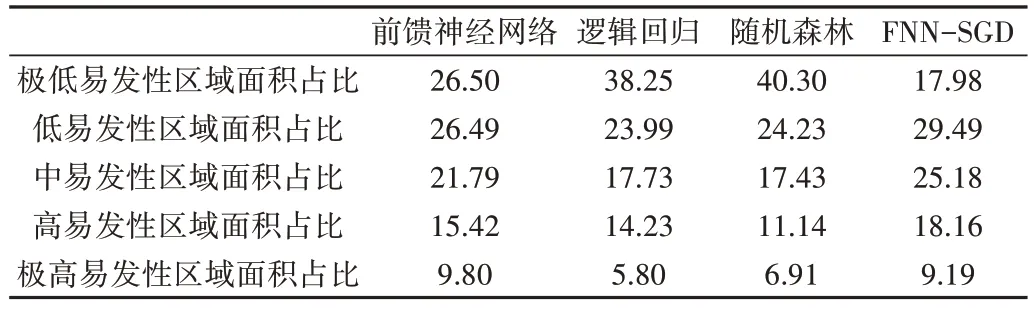
Table 3 Partition area proportion of the four models表3 4種模型所對應的分區面積占比情況 %

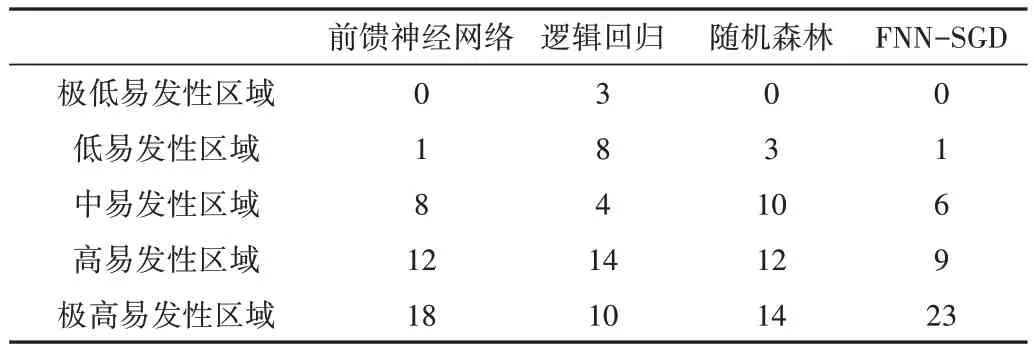
Table 4 Distribution of debris flow disaster points corresponding to the four models表4 4種模型所對應的分區泥石流災害點分布情況

3.3 模型結果驗證

驗證是雷波縣泥石流易發性評價中不可或缺的一部分，某種程度上決定了模型制圖質量。為更好地評估模型精度，使用ROC 曲線進行驗證。訓練集4 種模型的準確率ROC 曲線如圖8 所示，驗證集4 種模型的預測成功率ROC曲線如圖9所示。

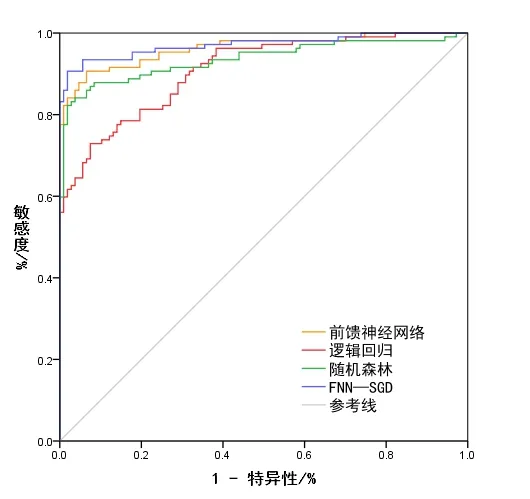
Fig.8 Accuracy ROC curve圖8 準確率ROC曲線

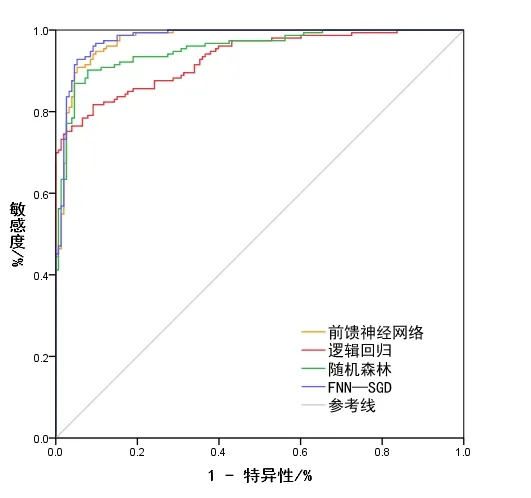
Fig.9 ROC curve for predicting success rate圖9 預測成功率ROC曲線

4 種模型的準確率及預測成功率如表5 所示。成功率與預測率之間的差值可體現模型的穩定性，按照差值由大到小排序，分別為邏輯回歸（2.2%）、隨機森林（1.8%）、前饋神經網絡（1.3%）、FNN-SGD（0.9%）。由此可知，FNN-SGD模型穩定性強、可靠，具有良好的泛化能力。

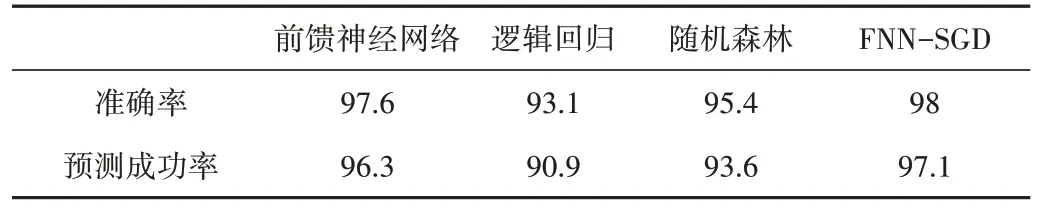
Table 5 Accuracy rate and prediction success rate of four models表5 4種模型準確率及預測成功率 %

因此，通過綜合考慮ROC 曲線驗證及泥石流在實際情況中易發性的對比分析，FNN-SGD 模型的準確率和預測成功率相比其他3 個單模型的效果更好，更適用于雷波縣泥石流易發性評價。根據FNN-SGD 模型的雷波縣泥石流易發性評價結果和區域重要程度兩方面進行分析，得出雷波縣的泥石流易發性區域。

4 結語

本文通過ROC 曲線對4 種模型的性能進行驗證，實驗結果表明，FNN-SGD 模型與前饋神經網絡、邏輯回歸和隨機森林相比，FNN-SGD 模型的準確率更高、穩定性更強。根據FNN-SGD 模型結果繪制雷波縣泥石流易發性分布圖，高和極高易發性區域主要分布于雷波縣東南部，中易發性區域主要分布于雷波縣東北部，低和極低易發性區域主要分布于雷波縣西北部。雷波縣泥石流易發性區域的具體分布情況為：高和極高易發性區域主要分布于雷波縣的巴姑鄉、寶山鎮、渡口鎮、卡哈洛鄉、馬頸子鎮、莫紅鄉、千萬貫鄉、上田壩鎮、永盛鎮；中易發性區域主要分布于雷波縣的桂花鄉、黃瑯鎮、箐口鄉、山棱崗鄉、瓦崗鎮、汶水鎮；低和極低易發性區域主要分布于雷波縣的柑子鄉、谷堆鄉、金沙鎮、錦城鎮、拉咪鄉、西寧鎮。

因此，相比于與其他3 種模型，FNN-SGD 模型得到的泥石流易發性分布圖具有更強的適應性與合理性。未來泥石流易發性評價研究還有待進一步深入，本研究的結論對于降低雷波縣區域性的泥石流風險及制定土地利用規劃具有一定借鑒意義。