結構影響線識別：反問題可識別性分析與降維貝葉斯不確定性量化

慕何青，龐振浩，王 浩，蘇 成

(1. 華南理工大學土木與交通學院，廣東，廣州 510641；2. 華南理工大學亞熱帶建筑科學國家重點實驗室，廣東，廣州 510641；3. 中國地震局工程力學研究所地震工程與工程振動重點實驗室，黑龍江，哈爾濱 150080；4. 東南大學土木工程學院，江蘇，南京 211189；5. 東南大學混凝土及預應力混凝土結構教育部重點實驗室，江蘇，南京 210096)

結構影響線描述了以移動單位集中荷載作為輸入、以指定截面靜力響應作為輸出的映射關系[1]，其直接反映結構的實際狀態。因此，結構影響線識別是移動荷載下既有結構評估的理論基礎[2]，已被廣泛地應用于結構損傷演化[3?6]、結構模型修正[7?9]、橋梁動態稱重[10?12]等方面。影響線識別方法主要分為兩類[2]：空間域方法和頻率域方法。在空間域方法中，OBRIEN 等[13]基于最小二乘法求解影響線函數的有限散點；YAMAGUCHI 等[14]在引入多項式函數來描述影響線的基礎上求解影響線函數；王寧波等[15]考慮多項式分段函數與橋梁動力效應消除；IENG[16]采用極大似然估計；陳志為等[17]結合正則化方法和三次B 樣條曲線方法，并在實驗室鋼筋混凝土橋梁試驗中驗證方法；ZHENG 等[18]提出正則化最小平方QR 分解法；KHUC 和CATBAS[19]針對橋梁橫向效應較大的寬橋提出基于迭代逼近進行影響面識別；ZHENG等[20]提出基于經驗模態分解的橋梁靜影響線識別方法；朱前坤等[21]基于計算機視覺識別人行橋撓度影響線；ZHOU 等[22]提出大數據和仿射區間分析方法；ZHENG 等[23]基于節點編碼重排將二維影響面識別轉化為一維影響線識別。在頻率域方法中，HUNT[24]提出通過消除多軸效應來提取橋梁影響線的方法；FR?SETH 等[25]提出頻域正則化濾波器進行影響線提取；YAN 等[26]提出靜力響應傳遞比函數法。

結構影響線識別本質上是基于系統輸入-輸出含噪數據反向對靜力系統指定截面的響應函數進行識別。已有研究雖然取得了進展，但它們在以下兩個方面存在局限性：1) 缺乏反問題可識別性分析；2) 缺乏不確定性量化。反問題可識別性分析是為了厘清系統識別的參數的解的情況。對于一般情況下未知函數形式的待識別影響線，其對應的參數向量的維度是無窮。由于無窮維參數是不可識別的，已有的識別方法的模型參數化形式可分成兩類：第一類是直接參數化，參數是加載位置對應的影響值[13,16,18]；第二類是間接參數化，參數是選定位置對應的影響值[14?15,17,19]。無論是哪一種參數化形式，嚴格地進行反問題可識別性分析都是影響線識別的前提。不確定性量化是基于測量輸入-輸出含噪數據估計影響線參數的后驗概率密度函數。已有識別方法一般是給出參數最優值估計。然而，實際工程通常伴隨著顯著的不確定性源(測量信息不完備、測量誤差、模型誤差、未知干擾等)，導致工程反問題的解同樣伴隨著顯著的不確定性。忽略這些不確定性將導致結構響應預測與評估的可靠性降低。

針對上述兩個局限性，本文在貝葉斯概率框架的基礎上開展關于影響線識別的反問題可識別性分析與貝葉斯不確定性量化。貝葉斯概率是基于貝葉斯理論表征觀測者對未知命題的置信度[27]。在工程力學系統識別領域，BECK 與KATAFYGIOTIS是建立貝葉斯概率框架的先驅者[28?33]。該概率框架被不斷發展并應用于不同問題，包括可靠度問題[34?35]、模態參數更新問題[36?37]、有限元模型修正[38?39]、系統模型選擇[40?41]等。

反問題可識別性分析(Model Identifiability)這一概念最初是由BECK 與KATAFYGIOTIS[28]提出。可識別性分析的對象是參數最優值，可識別性分析的定量指標是參數最優值的唯一性。反問題可識別性分析可建立在參數最大似然估計值的基礎上進行。該分析將模型可識別性分成全局模型可識別、局部模型可識別、模型不可識別三種情況。只有在全局模型可識別的前提下，反問題存在唯一解。貝葉斯不確定性量化是基于參數后驗概率密度函數。首先，本文進行基于直接參數化的影響線識別，包括系統輸入與輸出構造、反問題可識別性分析、參數最優值。經分析得出：一方面，直接參數化無法保證全局模型可識別；另一方面，現有方法即使是全局模型可識別的情況下也無法進行不確定性量化。然后，為保證反問題是全局模型可識別且同時獲取參數后驗概率密度函數，本文提出基于降維貝葉斯不確定性量化的影響線后驗識別，包括系統輸入與輸出重構、反問題可識別性分析、后驗概率密度函數。最后，本文進行新光大橋吊桿拉力影響線識別與簡支梁橋應變影響線識別，并驗證提出方法的有效性。

1 基于直接參數化的影響線識別

1.1 系統輸入與輸出構造

基于上述公式進行參數求解的前提是厘清參數的解的情況。橋梁影響線識別是一個反問題。該反問題在某些情況下是病態的(例如，參數的解有無窮多個)。病態反問題的求解結果是無法用于實際工程的。因此，在影響線識別之前，需要進行嚴格的反問題可識別性分析。

1.2 反問題可識別性分析

1.3 參數最優值

在全局模型可識別的情況下(情況3)，反問題存在唯一解。通過考慮?lnp(Φ|W,L)/??=0，參數最優值：

上述這種僅通過目標函數進行參數最優值估計的做法，是已有方法的普遍做法。然而，實際工程通常伴隨著顯著的不確定性源(測量信息不完備、測量誤差、模型誤差、未知干擾等)，導致工程反問題的解同樣伴隨著顯著的不確定性。忽略這些不確定性將導致結構評估與預測的可靠性降低。

為保證反問題是全局模型可識別且獲取參數后驗概率密度函數，本文在下一節提出基于降維貝葉斯不確定性量化的影響線后驗識別，包括降維參數化與基于貝葉斯定理的參數后驗概率密度函數。

2 基于降維貝葉斯不確定性量化的影響線后驗識別

2.1 基于降維參數化的系統輸入與輸出重構

降維參數化是間接參數化的一種，其目的在于引入不直接取決于數據測量方案的參數化形式，從而降低參數維度，提高全局模型可識別的可能性。

下面將對比直接參數化與降維參數化的反問題可識別性。

2.2 反問題可識別性分析

3 新光大橋吊桿拉力影響線識別

本節應用提出的降維貝葉斯估計進行新光大橋吊桿拉力影響線識別。為了檢驗提出方法的有效性，首先，介紹系統輸入與輸出數據；然后，對比不同工況(不同數據與降維模型)的影響線識別效果；最后，對比不同降維互異位置向量(受“影響線參數位置間隔長度”控制，下文會具體描述)的影響線識別效果。

新光大橋是廣州市內跨越珠江主航道的一座特大型橋梁，該橋采用三角剛架與下承式無鉸系桿拱相結合的結構體系，為一座總跨徑S=782 m的三跨連續剛構中承式拱橋，其跨徑組合為177 m+428 m+177 m(圖1(a))[43]。吊桿是新光大橋的重要受力構件，其主要承受橋面系傳來的豎向荷載。該橋共設置6 條車道，包括3 條上行車道和3 條下行車道，車道布置如圖1(b)所示。

圖1 新光大橋概況 /m Fig. 1 Overview of the Xinguang Bridge

系統輸入與輸出數據是車輛荷載與含噪荷載效應。車輛荷載以模擬車隊的形式進行加載[44]。車隊代表車型采用《公路橋涵設計通用規范》[45]的五軸車：其前軸至后軸的軸距分別為3 m、1.4 m、7 m、1.4 m，第一軸至第五軸的軸重分別為30 kN、120 kN、120 kN、140 kN、140 kN(總重550 kN)。車隊交通流考慮車隊車輛數Q(單位：輛)和時變車間距d(后車與前車的距離，單位：m)。其中代表車型、Q、d都可根據實際情況進行調整。為了檢驗提出方法在不同車輛荷載下的影響線識別效果，車流數Q取Q20 與Q80 兩種情況，分別對應20 輛車與80 輛車；隨機車間距d考慮d80 與d100 兩者情況，分別對應均值為80 m 與100 m、標準差都為1 的高斯分布，因此，一共有Q20-d80、Q20-d100、Q80-d80、Q80-d100 這4 種車輛荷載情況。荷載效應選取C1 車道(圖1(b))對應的主跨跨中吊桿(見圖1(a)中5#)拉力。荷載效應數據通過將上述車隊加載到主跨跨中吊桿對應C1 車道的影響線獲取。荷載效應采樣開始于車隊首輛車進入橋梁，采樣間隔為車隊首輛車每前進10 m，采樣結束于車隊末輛車離開橋梁。含噪聲的荷載效應獲取如下：基于車輛荷載與影響線獲得未含噪聲的荷載效應，在此基礎上疊加噪聲獲得含噪聲的荷載效應。噪聲通過隨機采樣獲取，其服從獨立高斯分布：均值為0，標準差為未含噪聲的荷載效應數據集標準差的5%(對應的是5%的噪聲水平)。

通過考慮兩種降維模型(2.1 的第1 降維模型(m1)與第2 降維模型(m2))與4 種數據(Q20-d80、Q20-d100、Q80-d80、Q80-d100)與的組合，獲得8 種工況(m1-Q20-d80、m1-Q20-d100、m1-Q80-d80、m1-Q80-d100、m2-Q20-d80、m2-Q20-d100、m2-Q80-d80、m2-Q80-d100)，并對比它們的影響線識別效果。兩種降維模型基于同樣的降維互異位置向量X：X={xi|xi=?x.i,i=0,1,···,floor,xceil=S,floor=?S/?x」,ceil=「S/?x?}，其中 ?.」 與 「.?分別是向下與向上取整函數， ?x為影響線參數位置間隔長度(單位：m)，此處設?x=10。

表1 匯總了車輛荷載工況與降維貝葉斯方法參數工況。圖2 展示了不同工況的識別影響線后驗最優值與后驗95%置信區間。需要說明的是，后驗95%置信區間是基于后驗(p+1)維的高斯分布G(mΘ?,mΣ?)得出。該圖同時展示了實際影響線用于識別值與實際值的對比。圖2(a)和圖2(c)分別展示了第1 和第2 降維模型的后驗最優值；圖2(b)和圖2(d) 分別展示了第1 和第2 降維模型的后驗95%置信區間。結果表明：1)本文提出的兩個降維模型的影響線最優值與不確定性量化結果均能滿足實際結構影響線識別；2)第2 降維模型比第1 降維模型更優—它能獲取更準確的函數峰值區域后驗估計值與給出更小的后驗置信區間。圖3給出了不同工況的識別影響線識別殘差絕對值與標準差的箱線圖。箱線圖從上到下五條線依次是：最大值、四分之三等分點、二分之一等分點(中位數)、四分之一等分點、最小值。其中，圖3(a)殘差絕對值箱線圖是基于圖2(a)與圖2(c)；圖3(b)標準差箱線圖是基于圖2(b)與圖2(d)。結果表明：1)對于同一個降維模型，交通流Q和車輛間距d增大，殘差絕對值與標準差兩者的中位數與波動范圍會相應降小；2)第2 降維模型比第1 降維模型更優—這與圖2 的結論一致。上述結果背后的原因是：在[0,300]與(482,782]的區域，真實影響線幾乎為0，該段區域兩個降維模型的結果類似；在[300,482]的區域，真實影響線非常陡峭，第1 降維模型假設 ?x內影響線為常數限制了其表現、而第2 降維模型假設 ?x內影響線為直線滿足要求。在一般情況下，如果存在多個降維模型，擁有更多參數的降維模型由于解的空間更大，所以它能更好地擬合影響線數據。

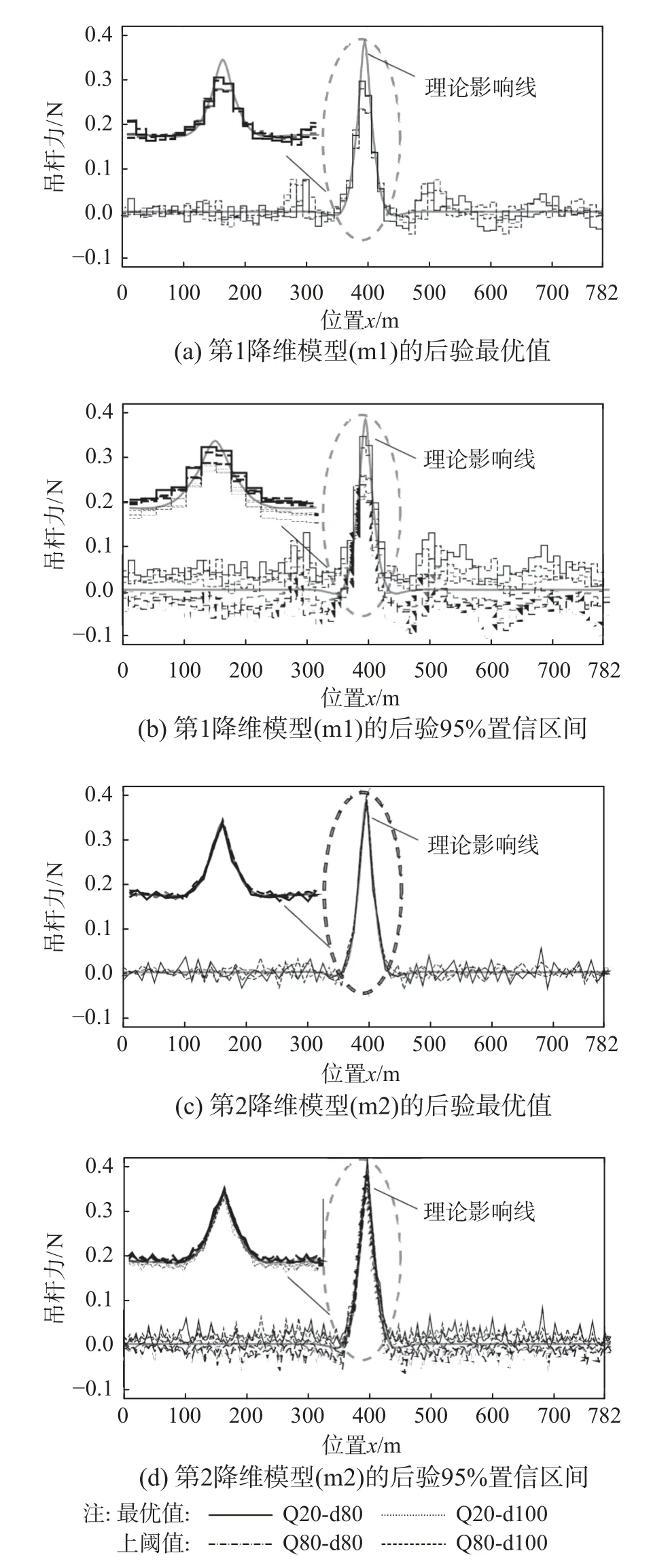
圖2 不同工況的識別影響線后驗最優值與后驗95%置信區間Fig. 2 Posterior optimal values and 95% confidence intervals of identified influence lines of different cases

圖3 不同工況下識別影響線的殘差絕對值與標準差箱線圖Fig. 3 Box plots of absolute values of residuals and standard deviations of identified influence lines of different cases

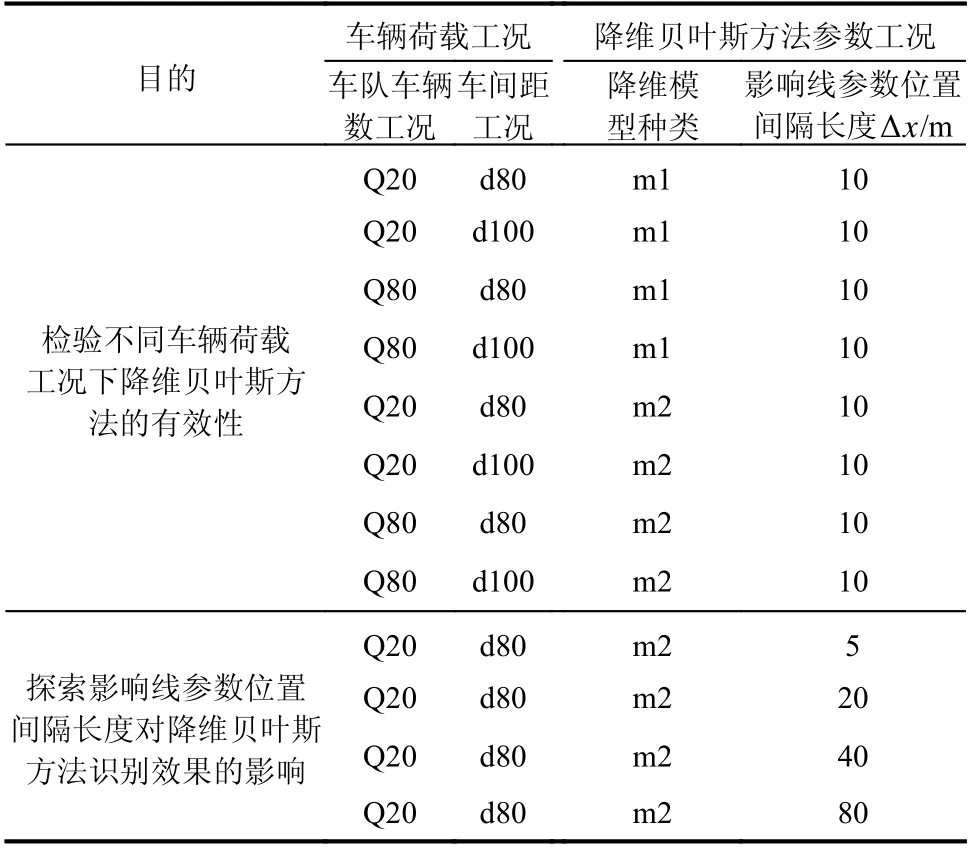
表1 車輛荷載工況與降維貝葉斯方法參數工況Table 1 Different cases of vehicle loads and parameters of reduced-dimension Bayesian uncertainty quantification

為了對比不同降維互異位置向量的影響線識別效果，對m2-Q20-d80 工況考慮不同的?x={5,10,20,40,80}。圖4 展示了m2-Q20-d80 工況下不同參數位置間隔長度的識別影響線的殘差絕對值與標準差箱線圖。可以看出：1) ?x從10 減小到5，識別效果變差；2) ?x從10 增加到80，識別效果變差。以下對上述結果進行解釋：一方面，?x減小，參數數目增加，但每個 ?x內的荷載樣本量減少—等價于參數識別的數據信息減少；另一方面， ?x增加，參數數目降低—等價于參數解空間的維度降低。因此， ?x的選擇區間不宜過大或過小。在此工況下， ?x的合適選擇區間是[10,20]。此區間內，降維貝葉斯的影響線識別結果能兼顧穩定性與準確性。一般情況下，建議以橋梁最小跨徑的5%～10%為 ?x的初始選擇，通過減小或增加 ?x，觀測識別結果的變化，最終結合工程判斷進行選取。

圖4 m2-Q20-d80 工況下不同參數位置間隔長度的識別影響線的殘差絕對值與標準差箱線圖Fig. 4 Box plots of absolute values of residuals and standard deviations of identified influence lines by different interval lengths of position of parameter under the case of m2-Q20-D80

4 簡支梁橋應變影響線識別

本節基于簡支梁橋實測數據[2,17]與模擬數據，對應變影響線進行識別。該簡支梁試驗橋梁跨徑為25 m，采用等截面形式，截面彈性模量EI=9.3×107kN·m2，應變計安裝于跨中。加載車輛為四軸車輛，第2～4 軸與第1 軸的距離分別為1.95 m、6.20 m 和7.60 m，第1～4 軸的軸重分別為11.9 t、11.9 t、23.9 t 和23.9 t。卡車的位置由安裝在加載車輛前軸上方的GPS 傳感器采集，車輛行駛速度為1 m/s，采樣頻率為10 Hz。實測輸入數據來自于車輛軸重與定位GPS 傳感器。實測輸出數據來自于跨中應變計采集數據集。模擬輸出數據來自于未含噪聲的模擬應變疊加噪聲，其中：未含噪聲的模擬應變通過實測輸入數據下進行跨中應變理論影響線加載獲得；噪聲通過隨機采樣獲取，其服從獨立高斯分布：均值為0，標準差為未含噪聲的荷載效應數據集標準差的5%(對應的是5%的噪聲水平)。

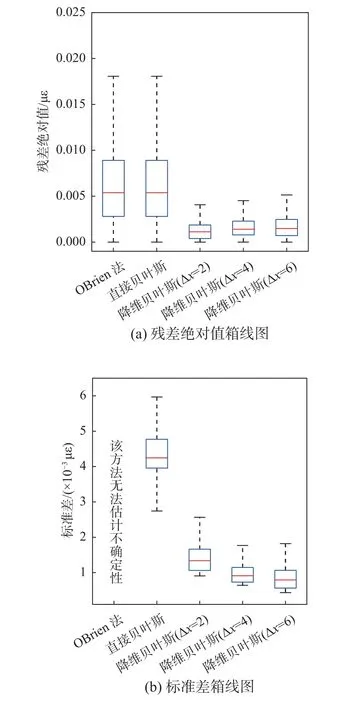
本文對比了三種方法：1) OBrien 提出的最小二乘法[13](記為：OBrien 法)；2)基于直接參數化的貝葉斯方法[16](記為：直接貝葉斯)；3) 本文提出的降維貝葉斯方法(記為：降維貝葉斯)。其中，OBrien 法形式與式(10)等價；直接貝葉斯僅考慮第1 小節的直接參數化(也就是，不考慮2.1 小節的參數降維)，在式(5)的基礎上直接引入貝葉斯概率框架，獲取非降維參數的后驗概率密度函數：其服從于一個h維的高斯分布—其均值與OBrien 法獲得的最優參數一致、其協方差矩陣為Fisher Information 矩陣。降維貝葉斯采用第2 降維模型(m2)，其背后原因是跨中應變影響線理論上為折線。需要注意的是：1) 前兩者方法對應的參數維度是h，而本文提出的降維貝葉斯對應的降維參數維度是p(p

圖5 展示了實測數據和模擬數據下三種方法的識別影響線。圖5(a)展示了跨中應變實測數據和模擬數據，其中，橫軸表示加載車輛第1 軸位置；圖5(b)、圖5(c)和圖5(d)分別是OBrien 法、直接貝葉斯和降維貝葉斯(?x=4)對應的影響線識別結果。結果表明：1)影響線最優值方面，相對于OBrien 法和直接貝葉斯，降維貝葉斯的結果更準確且更平滑；2)影響線不確定性量化方面，OBrien 法無法給出置信區間、直接貝葉斯可以給出置信區間、降維貝葉斯的置信區間更平滑。這些結果均表明，參數降維與貝葉斯不確定性量化是改善影響線識別效果的兩個重要因素；3)模擬數據與實測數據對應的影響線識別結果存在差異，這一點結論與論文[2,17]一致。通常情況下，實測過程中會存在許多未知的不確定性源，這更表明需要引入貝葉斯概率框架對影響線識別結果進行不確定性量化。

圖5 實測數據和模擬數據下三種方法的識別影響線Fig. 5 Identified influence lines by three different methods using measured and simulated datasets

圖6 展示了模擬數據下三種方法的識別影響線的殘差絕對值與標準差箱線圖。同時，為討論參數 ?x(即：影響線參數位置間隔長度)取值對降維貝葉斯的影響，本文對降維貝葉斯考慮三種參數工況： ?x=2,4,6。可以看出：1)對于圖6(a)殘差絕對值箱線圖，一方面，OBrien 法與直接貝葉斯一致—這是因為它們兩者都是基于同樣的直接參數化，因此兩者的最優值與殘差都一致；另一方面，不同工況下降維貝葉斯的殘差各分位數結果更低，比前兩種方法都好；2)對于圖6(b)標準差箱線圖，OBrien 法無法估計不確定性；直接貝葉斯可以估計標準差；不同工況下降維貝葉斯的標準差各分位數更低，比直接貝葉斯更好；3)影響線參數位置間隔長度的選取在合理范圍內，降維貝葉斯的影響線識別結果能兼顧穩定性與準確性。

圖6 模擬數據下三種方法的識別影響線的殘差絕對值與標準差箱線圖Fig. 6 Box plots of absolute values of residuals and standard deviations of identified influence lines by three different methods using simulated datasets

5 結論

本文在貝葉斯概率框架的基礎上開展關于影響線識別的反問題可識別性分析與貝葉斯不確定性量化。反問題可識別性分析是建立在均勻先驗的參數后驗最優值的基礎上將模型可識別性分成全局模型可識別、局部模型可識別、模型不可識別三種情況。只有在全局模型可識別的前提下，反問題存在唯一解。為保證反問題是全局模型可識別且同時獲取參數后驗概率密度函數，本文提出基于降維貝葉斯不確定性量化的影響線后驗識別。本文的主要結論如下：

(1)直接參數化無法保證全局模型可識別；現有方法即使是全局模型可識別的情況下也無法進行不確定性量化。

(2)降維參數化可保證反問題是全局模型可識別的；可基于貝葉斯定理獲得參數后驗概率密度函數。參數降維與貝葉斯不確定性量化是改善影響線識別效果的兩個重要因素。

(3)如果存在多個降維模型，擁有更多參數的降維模型由于解的空間更大，因此能更好地擬合影響線數據。影響線參數位置間隔長度的選取在合理范圍內，降維貝葉斯的影響線識別結果能兼顧穩定性與準確性。一般情況下，建議以橋梁最小跨徑的5%～10%為間隔長度的初始選擇，通過減小或增加間隔長度，觀測識別結果的變化，最終結合工程判斷進行選取。