數學文化在中考數學試題中的滲透
——以2018—2022年寧波市中考數學為例

徐 爭 張維忠

(浙江師范大學教師教育學院 321004)

《義務教育數學課程標準(2022年版)》強調數學課程要以核心素養為導向，關注數學文化，繼承和弘揚中華優秀傳統文化，同時反映現代科技與社會發展需要[1]．張維忠教授提出課程中的數學文化具有豐富聯系，可從縱橫兩個方向理解數學與外部的聯系，縱向指的是與學生數學學習文化背景及數學現實間的聯系，橫向指的是與其他學科間的聯系[2]，他將高考中的數學文化分為數學與生活、數學史、數學與科技、數學與藝術四類[3]．唐恒鈞教授根據數學文化運用水平將其統一為附加型、整合型，其中整合型可細分為可分離型和不可分離型[4]．

浙江省初中學業水平考試數學試題以義務教育數學課程標準和浙教版初中數學教材為命題依據，強調對學生數學核心素養的有效考查．數學文化在數學試題中的重要性不斷提高，而近年來寧波市推動初中教育高質量發展，數學文化類試題、情境應用題也成為寧波市初中學業水平考試數學試題的一大亮點，旨在培養學生數學核心素養，突出數學學科育人價值．本文以近五年寧波市中考數學試題為例，從數學與生活、數學史、數學與科技、數學與藝術四個方面，對數學文化試題進行評析，以期為中考數學試題命制提供一些建議．

1 試題特征

表1是2018—2022年寧波市中考數學有關于數學文化試題的統計．

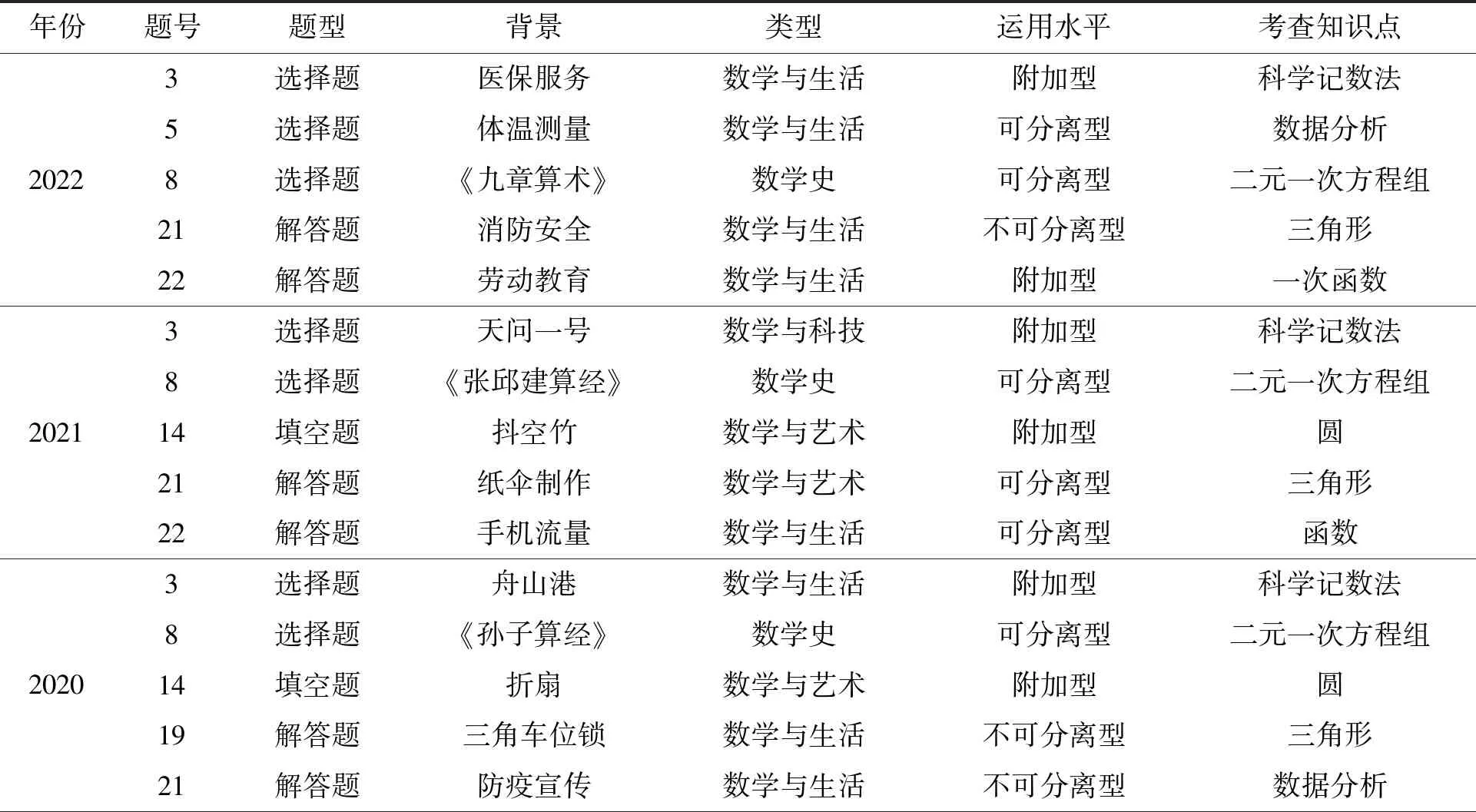
表1 2018—2022寧波市中考數學卷中的數學文化試題

續表

這五年的寧波市中考數學卷涉及數學文化試題共20題，在內容分布上具有以下特征：

(1)試題數量方面，2018年2題，2019年3題，約占10%；2020—2022年都有5題，約占22%．由此可見，數學文化試題越來越受寧波市中考數學命題者的重視．

(2)題型設置方面，2018年、2019年、2022年主要為選擇題及解答題，2020—2021年選擇題、填空題及解答題都有涉及．題型的設置基本不變，主要側重點為選擇題、解答題上的考查．

(3)試題背景方面，試題背景既有考試當年的時事熱點，如醫保服務、防疫宣傳等，也有體現中華民族優秀傳統文化的著作，如《九章算術》等，以及寧波本地文化，如舟山港等，還有中華優秀民間藝術，如抖空竹、紙傘制作、折扇等．

(4)類型方面，數學與生活相關的試題較多，共12題，約占60%；其次是數學史和數學與藝術，依次為4題與3題，分別占20%和15%；最少的是數學與科技類試題，僅1題．表明寧波市中考數學命題者更加重視數學與生活之間的聯系，但需要加強對科技與數學試題結合的重視．

(5)運用水平方面，試題以可分離型和附加型為主，共17題，約占85%，其中可分離型6題、附加型11題.這表明試題命制時沒有很好地將數學文化與數學試題有機融合，做到用數學解決文化中存在的問題.

(6)考查知識點方面，試題每年考查的知識點與題型基本類似，主要集中在科學記數法、數據分析、三角形、二元一次方程組、函數、圓這幾部分內容．試題難度基本不大，屬于基礎題，主要考查學生對基礎知識的掌握與應用程度．

2 2018—2022年數學文化試題賞析

2.1 數學與生活

例1(2022·寧波)每年的11月9日是我國的“全國消防安全教育宣傳日”，為了提升全民防災減災意識，某消防大隊進行了消防演習．如圖1，架在消防車上的云梯AB可伸縮(最長可伸至 20 m，且可繞點B轉動，其底部B離地面的距離BC為2 m，當云梯頂端A在建筑物EF所在直線上時，底部B到EF的距離BD為9 m．

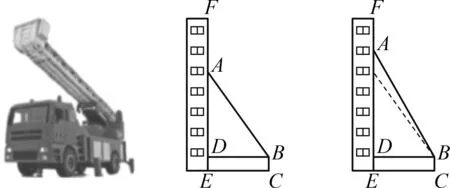
圖1 圖2

(1)若∠ABD=53°，求此時云梯AB的長；

(2)如圖2，若在建筑物底部E的正上方19 m處突發險情，請問在該消防車不移動位置的前提下，云梯能否伸到險情處？請說明理由．

(參考數據：sin 53°≈0.8，cos 53°≈0.5， tan 53°≈1.3)

評析關注消防就是關愛生命，11月9日恰好與火警電話119相同，因此1992年起我國將11月9日定為全國消防安全教育宣傳日，以增強大家對消防安全的重視，提升全民防災減災意識．本題基于消防安全背景，將消防演習與三角形知識有機融合，考查學生對銳角三角函數的掌握．既使學生能夠利用直角三角形的知識解題，也能讓學生在解題時感受數學在消防中、生活中的應用，即如何利用數學知識進行消防搶救，感受數學的魅力，更加重視消防安全與人身安全．

例2(2020·寧波)某學校開展了防疫知識的宣傳教育活動．為了解這次活動的效果，學校從全校1 500名學生中隨機抽取部分學生進行知識測試(測試滿分100分，得分x均為不小于60的整數)，并將測試成績分為四個等第：基本合格(60≤x<70)，合格(70≤x<80)，良好(80≤x<90)，優秀(90≤x≤100)，制作了如圖3的統計圖(部分信息未給出)．

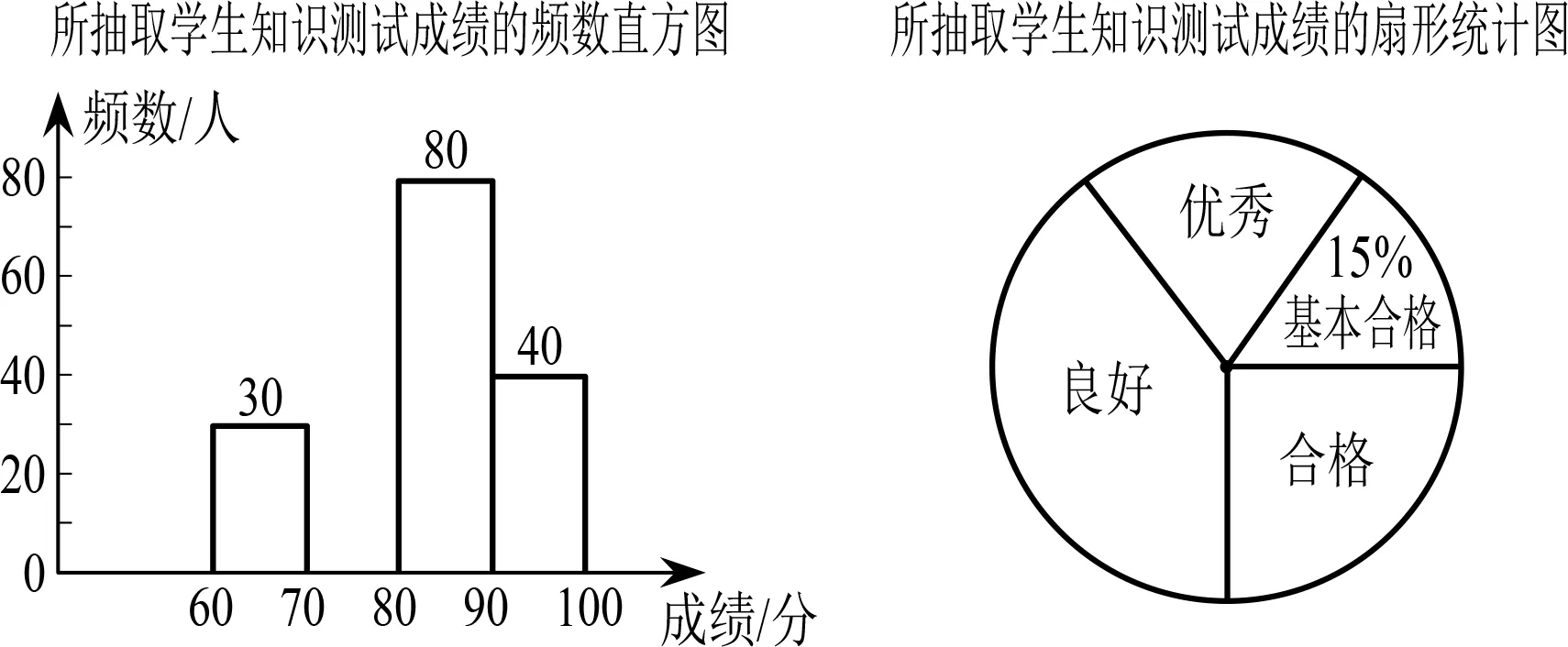
圖3

由圖中給出的信息解答下列問題：

(1)求測試成績為合格的學生人數，并補全頻數直方圖；

(2)求扇形統計圖中“良好”所對應的扇形圓心角的度數；

(3)這次測試成績的中位數是什么等第？

(4)如果全校學生都參加測試，請你根據抽樣測試的結果，估計該校獲得優秀的學生有多少人.

評析數學源于生活，又應用于生活．2020年由于新型冠狀病毒肺炎的出現，全國各省市各級學校紛紛開展防疫工作，保證師生健康．防疫宣傳在疫情防控中起到重要作用，本題就以防疫宣傳為背景，考查學生對頻數分布直方圖、扇形統計圖及中位數等知識的掌握程度，培養學生數據觀念、運算能力等方面的數學核心素養．學生也能在解題中進一步增強防疫知識，并激起對抗擊疫情一線的醫務工作人員和社會各界人士的敬意．

2.2 數學史

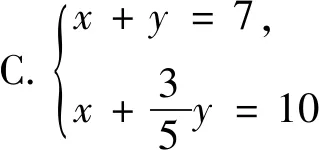
評析《九章算術》是中國古代數學的重要著作之一，它的出現標志著中國古代數學體系的形成．《九章算術》共九章，記錄了246個數學問題，取得了豐碩的數學成果．浙教版七年級下冊第二章閱讀材料部分就專門介紹了《九章算術》中的“方程”．本題以《九章算術》為背景材料，選取其中一個數學問題，要求學生能從實際問題中抽象出二元一次方程組得到對應的等量關系，即原來的米加后來的谷子為10斗，原來的米加后來的谷子舂成的米為7斗，考查學生的數學抽象能力．《九章算術》中的題目多為社會生產生活問題，學生通過本題能夠感受古代勞動人民與數學家的智慧，了解中華優秀傳統文化，增強民族自豪感與文化自信．

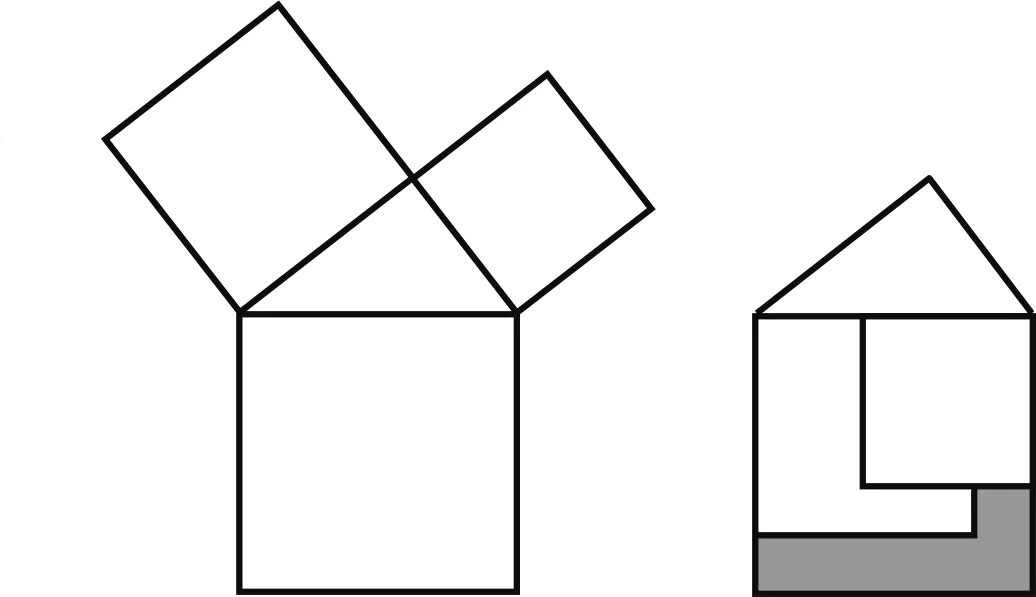
圖4 圖5

例4(2019·寧波)勾股定理是人類最偉大的科學發現之一，在我國古算書《周髀算經》中早有記載．如圖4，以直角三角形的各邊為邊分別向外作正方形，再把較小的兩張正方形紙片按圖5的方式放置在最大正方形內．若知道圖中陰影部分的面積，則一定能求出( )．

A．直角三角形的面積

B．最大正方形的面積

C．較小兩個正方形重疊部分的面積

D．最大正方形與直角三角形的面積和

評析《周髀算經》同樣是我國傳統數學的重要著作，是算經的十書之一，主要成就是記載了商高同周公的對話，“勾三股四弦五”，即勾股定理．學生在八年級上冊學習了勾股定理，但學生往往只了解商高、趙爽弦圖、畢達哥拉斯定理，對《周髀算經》并不熟悉．本題就對勾股定理的背景進行了強有力的補充，主要考查勾股定理的應用及陰影面積的求法，屬于中難題．學生需要根據勾股定理、正方形面積公式得出陰影面積的表達式，再與選項中的面積相比較，進而得出答案．本題以學生掌握的勾股定理為出題方向，培養學生的運算能力、推理能力，同時也能提升學生對傳統數學著作和成果的認識，增強數學學習興趣．

2.3 數學與藝術

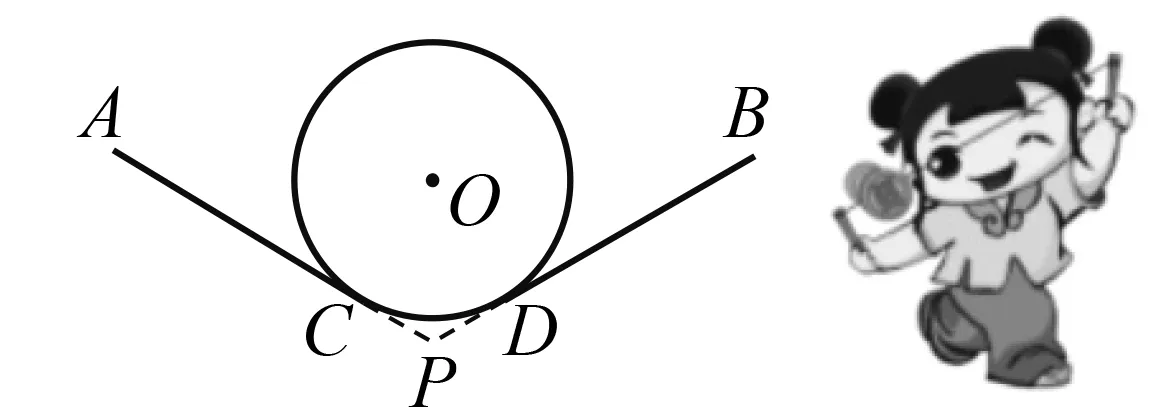
圖6

評析抖空竹流行于北京等地，歷史悠久，是國家級非物質文化遺產之一，具有重要的傳承價值，同時也是雜技藝術的重要表演形式．對江浙滬的學生而言，抖空竹相對來說比較陌生，它需要四肢巧妙配合，有利于鍛煉者的身體健康．本題以抖空竹為背景，主要考查學生對切線性質、弧長計算的掌握程度，解題關鍵就在∠COD的值．本題既能提高學生的抽象能力、運算能力，也能吸引學生繼續了解民間傳統藝術，感受中華五千年的文化孕育，加強文化自信．

2.4 數學與科技

例6(2021·寧波)2021年5月15日，“天問一號”著陸巡視器成功著陸于火星烏托邦平原，此時距離地球約320 000 000 km．數320 000 000科學記數法表示為( )．

A．32×107B．3.2×108

C．3.2×109D．0.32×109

評析2021年中國進行首次火星探測，天問一號探測器成功著陸，實現中國航天發展史上的6個首次，展現中國在航天發展上的創新和突破，標志著中國航天史上的重大進步．未來若干年，中國將繼續實施行星探測工程，陸續實施天問二號、三號等任務，完成科學研究，實現技術的遞進式發展．本題屬于基礎題，以天問一號著陸為背景，主要考查學生對科學記數法的掌握，提升學生運算能力及民族自豪感．

3 總結與建議

通過對2018—2022年寧波市中考數學試題的分析，我們可以發現，以寧波市為代表的中考數學命題越來越注重時事熱點，重視數學文化在中考數學試題中的滲透．這有利于強化課程的育人導向，培養學生核心素養，同時提升學生民族自豪感，增強文化自信．但存在以下幾個問題：(1)數學文化試題分布并不均衡，題目大多集中在數學與社會生活．我國的科技事業不斷發展，創新能力大大增強，但無論是寧波市中考還是其他省市中考，都較少體現數學與科技間的聯系；(2)每年涉及數學文化的試題與題型基本類似，如2018—2022年都在科學記數法考點設置數學文化背景，2020—2022年都在二元一次方程組上設置數學史背景等，數學文化在中考試題中的滲透較單一，新穎度不夠．基于以上結論，本文提出以下建議．

3.1 命題關注最新科技成果與傳統藝術

2022年全國乙卷理科卷就以嫦娥二號衛星、古代建筑為命題背景，中考數學命題同樣可關注長征二號運載火箭發射成功、探索二號科考船深海科考等最新科技成果，以及書法、音樂、繪畫、戲曲等方向的傳統藝術，凸顯中華文化底蘊，體現新時代中國力量，提高民族自信．同時使得考查形式靈活新穎，培養學生發現問題、分析問題、解決問題的能力，提升學生數學核心素養．

3.2 命題注重學科間融合

數學文化不僅體現在數學領域，還體現在其他學科中．比如高考數學命題中就曾將美術中的斷臂維納斯與黃金分割有機結合、將音樂中的鋼琴基礎知識與數列有機結合等，實現學科間的交流與互動，讓學生體會數學的基礎作用，感受數學文化的獨特魅力．

3.3 命題挖掘教材中的數學文化

浙教版、人教版等各版本的初中數學教材中都有不少的數學文化素材，比如數學家生平、數學家成果、數學家故事、數學著作等，這些都可以作為中考數學試題命制的重要來源．試題命制者可以挖掘教材中的數學文化，將其有機融入到數學試題中，讓學生更加重視教材，更加了解數學史，繼承與弘揚中華優秀民族文化．