一道課本不定方程應用題的運用

?福建省三明市明溪縣城關中學 楊發寧

1 課本原題

(人教版七年級下冊第112頁)

例1現有1角、5角、1元硬幣各10枚，從中取出15枚，共值7元.1角、5角、1元硬幣各取多少枚[1]？

分析：先設三種硬幣的數量分別為x，y，z，再利用已知的等量關系列出三元一次方程組并解方程組，然后由整除性質即可確定所求整數解問題的答案.

解法一：設1角、5角、1元的硬幣分別取x枚、y枚、z枚，那么

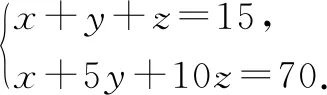
①

②

而x,y,z都為正整數，且z<7，1+9z是4的倍數，則z=3.此時y=7，x=5符合題意.

所以1角取5枚，5角取7枚，1元取3枚.

解法二：設1角、5角、1元的硬幣各取x枚、y枚、z枚，根據題意，得

③

④

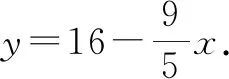
由x，y，z都為不小于10的整數，可知x=5或10.

當x=5時，y=7，z=3，符合題意.

當x=10時，y=-2，z=7，不符合題意.

所以，1角取5枚、5角取7枚、1元取3枚.

下面主要以近年“中考題”為例作些剖析.

2 在選擇題中的應用

例2(2020年黑龍江龍東中考)在一次知識競賽中，為嘉獎成績突出的同學，主辦方計劃用200元采購a，b，c三種文具，其中a種文具的單價為每個10元，b種文具的單價為每個20元，c種文具的單價為每個30元，在所有錢都剛好用完且c種文具不多于兩個的情況下，有多少種采購方案( ).

A.8種 B.10種 C.12種 D.14種

分析：根據題目文字得到兩個關鍵信息——購買三種獎品的總金額為200元；c種獎品個數為1或2.根據題目需要設出兩個未知數，得出一個二元一次方程，再根據二元一次方程的解都為整數及a，b，c的實際意義確定二元一次方程的解.

解：設購買a種獎品m個，b種獎品n個.

當c種獎品個數為1時，根據題意得10m+20n+30=200，即m+2n=17.

因為m，n都是正整數，則0<2n<17，所以n=1，2，3，4，5，6，7，8.

當c種獎品個數為2時，根據題意得10m+20n+60=200，即m+2n=14.

因為m，n都是正整數，則0<2n<14，所以n=1，2，3，4，5，6.

綜上所述，共有8+6=14種購買方案.故選：D.

點評：解題的第一步應該了解題目的含義，找出題目的關鍵信息；再根據題意設未知數列出方程或方程組；最后根據實際意義，由方程的解為自然數，得出符合題意的解.

3 在填空題中的應用

例3(2020年黃石中考改編)數學課上何老師講到我國古代的數學成就——《九章算術》，書中有這樣一個數學問題：“今有牛五、羊二，直金十九兩；牛二、羊五，直金十六兩．問牛、羊各直金幾何？”翻譯成現代文：“今知道5頭牛和2只羊，加起來一共價值19兩銀子；2頭牛和5只羊，加起來一共價值16兩銀子問每頭牛、每只羊分別值銀子多少兩？”．如果某商人準備用19兩銀子買牛和羊(要求既有牛也有羊，且銀兩須全部用完)，那么商人的購買方法共有種，列出所有的可能購買方案．

分析：先根據題意求出每頭牛、每只羊值的銀子數；再根據“19兩銀子購買牛、羊”列一個二元一次方程，求出這個二元一次方程的整數解即可.

解：設每頭牛值x兩銀子，每只羊值y兩銀子.

所以每頭牛值3兩銀子，每只羊值2兩銀子．

設19兩銀子購買a頭牛，b只羊.

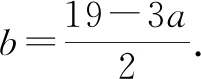
因為a，b都是正整數，所以a=5或3或1.即當a=5時，b=2；當a=3時，b=5；當a=1時，b=8.

所以，商人共有三種購買方法.購買5頭牛，2只羊；購買3頭牛，5只羊；購買1頭牛，8只羊．

點評：本題主要考查了運用二元一次方程(組)解決實際問題的能力.首先根據題意列出二元一次方程組并解之，求出牛與羊的單價；再根據題意列出一個二元一次方程即不定方程，根據實際意義與整除的性質，求出不定方程的正整數解.

4 在解答題中的應用

例4(2021年杭州模考)現有120 t口罩要運輸到上海抗疫救災，可供選擇的車型有甲、乙、丙三種，三種車的具體信息如表1所示：

表1 每輛車的運載能力和運費信息

(1)為提高運送效率，可以調用甲、乙、丙三種車型參與運送，每輛車均滿載，已知它們的總輛數為16，你能使用方程組求出所有可能的運送方案嗎?

(2)哪種方案的運費最少?最少是多少元?

分析：(1)設甲型車有x輛，乙型車有y輛，丙型車有z輛，列出方程組，再根據x，y，z均為非負整數，從而得出答案.

(2)根據(1)中方案得出運費，進行比較即可.

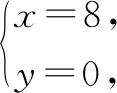
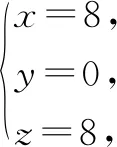
所以有三種運送方案：甲型車8輛，丙型車8輛；甲型車6輛，乙型車5輛，丙型車5輛；甲型車4輛，乙型車10輛，丙型車2輛.

(2)三種方案的運費分別為

400×8+600×8=8 000(元)；

400×6+500×5+600×5=7 900(元)；

400×4+500×10+600×2=7 800(元).

因為8000>7900>7800，所以調用甲型車4輛，乙型車10輛，丙型車2輛時運費最少，且最少是7 800元.

點評：本題涉及三個未知數，但只有兩個等量關系，只能列出兩個三元一次方程，可先消元，將兩個三元一次方程轉化為一個二元一次方程，再用含一個未知數的式子表示另一個未知數，利用整體思想和篩選法討論未知數的實際意義解決問題.

從上面的例子可以看出：通過一道課本簡單習題的解決，引出多道較難的中考題，我們感到課本習題大有可為.正如美國著名數學教育家G.波利亞所說：“數學問題的解決僅僅只是一半，更重要的是解題之后的回顧.”從簡單的題目中提煉解題方法，反思題目中的數學思想、解題策略，并變式研究是解題教學必不可少的環節.我們要以課本習題為藍本，分析題目的特征，認真研究解法，精選同類問題的變式進行適當訓練，歸納同類問題的通法.特別是近年來的一些中考題，因為中考題有一定的導向性和啟發性，反映中考命題方向和命題規律.通過“做”題的過程，對“列方程解應用題”進行系統復習，讓學生經歷獨立探究、思考、理性推理、深刻反思等數學活動過程，形成感性認識與理性思維的提升，培養學生語言文字與數學符號的轉化意識，構建方程模型解決實際問題的模式，完成知識構建，提升數學能力，發展學生數學素養核心素養，獲得適應個人終身發展和社會發展需要的必備品格和關鍵能力.