初中數學主題化跨單元教學設計
——以“三角形”的教學為例

?南京師范大學附屬中學樹人學校 劉春桃

1 問題的提出

推行“雙減”政策，要建立高質量的教育體系，提升教育教學質量，充分發揮課堂主渠道的作用，實現課堂的“減負增效”.隨著新課標的頒布和教改的不斷深入，單元式教學、項目式教學、跨學科式教學等新的教學模式應運而生，在“雙減”背景下，重新審視這些教學模式，單元式教學是實現課堂提質增效的最佳途徑[1]，且易為大多數教師所接受和實施，但這種教學模式在具體實踐過程中仍然存在斷層式或零散式現象，學生對于知識的學習依然處于碎片化、淺層次狀態.事實上，數學知識之間存在橫向或縱向的聯系，為了幫助學生構建完整的知識體系，厘清知識之間的聯系，提出主題化跨單元教學模式，在堅持“學生立場、單元視角、有機整合、高度拓展”基本原則的基礎上，對數學知識進行跨單元整合與拓展，打通“隔斷墻”，抓住核心素養，給與學生真實的“學習力”“生長點”，更能揭示相關數學知識之間的內在關聯，突出知識的系統性和教學的整體性、階段性和連續性，可以有效促進學生對數學知識的整體構建和核心素養的培養.本文中以“三角形”這一主題為例，具體探討主題化跨單元教學設計與實施策略.

2 教材分析

課堂教學的主要依據是教材.教師在進行教學設計和組織教學活動時，應反復研讀和深挖教材，厘清知識之間的聯系，這樣才能明確教學的重難點和目標，才能設計出切實可行的教學方案[2].

“三角形”主題化跨單元教學設計過程中，首先需要教師充分挖掘不同單元、不同學段的相關內容(如表1)，并在明晰前后知識點之間聯系的基礎上，進行系統化、整體化的思考與重構，形成跨單元教學思路.

表1 蘇科版初中數學“三角形”相關內容分布

“三角形”是整個初中階段數學學科的重點，也是高中數學學習的基礎.在蘇科版教材中，關于“三角形”這一主題知識點的聯系，主要表現在研究內容和研究方法兩個方面.

從研究內容上看，涵蓋三角形的確定、全等三角形的判定、相似三角形的判定和解三角形.其中，以三邊、三角的關系確定一個三角形是研究基礎，同時也是判定全等三角形的前提；而相似三角形則是全等三角形的進一步拓展和升華，全等三角形一定是相似三角形，但相似三角形不一定是全等三角形.而銳角三角函數則是建立在直角三角形中邊角之間關系的前提下，從代數的角度去分析三角形的特征.

從研究方法上看，全等三角形的判定和相似三角形的判定，都是從定性的角度去研究三角形的性質和特點.其中，全等三角形的判定定理是相似三角形判定的加強，而相似三角形的判定定理則是全等三角形的弱化.銳角三角函數則是從定量的角度去探究三角形的三條邊和三個角之間的關系.

3 數學教學案例設計

主題化跨單元設計理念下的數學教學核心是整體化和關聯化，要以同一主題將不同單元的內容有機串聯起來，通過對知識結構的整合和螺旋式思維的培育[3]，幫助學生構建完整的知識體系，從而有效解決前后斷層、重復、缺乏新舊知識銜接等諸多問題.基于教材分析，筆者構建了“三角形”主題跨單元內容結構圖(如圖1)，并按照知識點之間的聯系和學生認識水平，有序開展課堂教學活動.

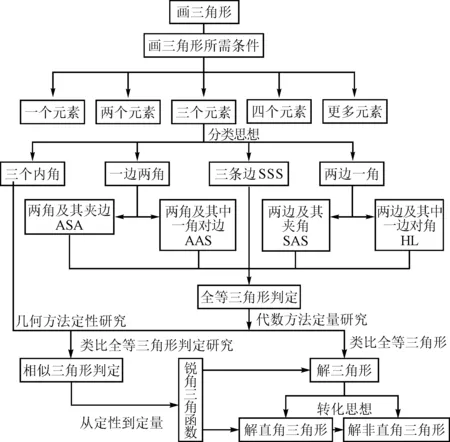
圖1 三角形主題跨單元教學結構內容圖

3.1 畫三角形，引導學生初步認識三角形

“認識三角形”是學生學習三角形的第一個單元，本單元教學的重難點是三角形的概念、分類、三邊關系及如何畫出滿足條件的三角形.為此，在這一環節，筆者以問題串的形式設計了“畫三角形”的探究性活動，將教學重難點融入其中，讓學生在動手、動腦的過程中突破知識難點.

問題1確定一個三角形需要幾個元素？

問題2給定兩個元素可以畫出符合條件的三角形嗎？

問題3給定三個元素能否畫出唯一確定的三角形？

問題4在不畫圖的前提下，若給定四個及以上元素能夠確定符合條件的三角形嗎？

設計意圖：通過問題串引導學生深入探究確定三角形所需的條件，明確在不同分類情況下的不同條件，在強化學生對三角形三邊與三角認知的同時，也為接下來的全等三角形和相似三角形的判定奠定基礎.

3.2 小組合作，探究三角形全等的判定條件

三角形全等的判定，在初中三角形主題的學習中起著承前啟后的作用，是相似三角形判定的重要依據.在主題化跨單元教學過程中，筆者繼續以問題串的形式，引導學生開展小組探究活動，深入學習三角形的特性.

問題5在分別給出1～4個及以上元素的情況下，哪種情況能夠構造出兩個大小與形狀完全一樣的三角形？

問題6能否結合圖形特征，嘗試給出全等三角形的定義與性質？

問題7你是如何判定兩個三角形全等的？有什么依據？

問題8如何尋找全等三角形及判定三角形全等的條件？

探究過程：在課前小測鞏固舊知的基礎上，以動手操作的活動形式，讓學生嘗試構建兩個大小且形狀相同的三角形，找出其中相等的邊和相等的角度，并思考如何判定兩個三角形全等.小組首先借助一副三角板合作探究給定1個元素(一條邊、一個角)和2個元素(兩邊、一邊一角、兩角)的情況，學生經歷操作、歸納得出1個元素、2個元素不能判斷兩個三角形全等的結論；繼續探索給定3個元素(三邊、兩邊一角、一邊兩角、三角)的情況，學生發現給出三邊、兩邊及其夾角、兩角及其夾邊或兩角及其中一角的對邊，可以得出兩個三角形全等的結論.學生交流討論后，教師再利用圖形及動畫進行展示，讓學生有更直觀的感受，最后師生共同歸納總結全等三角形的四種判定方法.

點評：提出問題時條件由少到多、由簡到繁，一步步深入、引導，通過一系列的活動最終得出三角形全等的條件.學生在合作探究中，提高了動手操作能力，有效突破了學習難點，并在小組合作中互幫互助，實現了資源的優質與均衡.

3.3 類比遷移，探究三角形相似的判定條件

從知識的橫向聯系來看，全等三角形是相似三角形的一種特殊情況，相似三角形則是全等三角形判定條件弱化后的進一步探究，二者之間有著極強的相似性.因此，筆者依然采取小組自主探究的方式，通過巧設問題，引導學生類比遷移尋找全等三角形判定條件的方法和思路，深入挖掘判定三角形相似的條件.

問題9閱讀教材，思考相似三角形與全等三角形之間有什么聯系與區別？

問題10猜一猜相似三角形的判定方法與全等三角形的判定方法是否會有聯系？

問題11 能否類比全等三角形判定的研究過程，探究相似三角形的判定條件？

問題12當兩個直角形相似時，它們的邊與角之間存在什么樣的關系？是否可以用邊之間的關系來描述直角三角形中銳角的大小？

設計意圖：在全等三角形的判定的學習中，學生已經體驗了畫三角形和用疊合法描述角相等、線段相等的過程，這為學生探究相似三角形提供了思路與方法.學生通過類比遷移，思考從全等三角形到相似三角形，哪些量不變？哪些量發生了變化？在變與不變中，學生運用相似的定義及預備定理，依照全等三角形判定的四種情形，逐一對相似三角形的判定條件進行探討，并得出結論.同時，借助問題12，構架了從相似三角形到銳角三角比概念的形成過程，實現了從“定性”向“定量”研究的過渡.

3.4 從特殊到一般，探究解三角形的方法

通過對教材的分析，我們發現全等三角形和相似三角形的學習，都是為解三角形作鋪墊，是用代數方法從量的角度對三角形的特征進行研究.

教學中，首先利用校園中的不可測量問題，引導學生從全等三角形、相似三角形等多角度思考解決問題的方法，即如何將“不可測量”問題轉化為“可測量”問題，揭示相似三角形與銳角三角比之間的密切聯系.沿著古人的足跡，師生共同探究、發現：在直角三角形中，當銳角固定時，銳角的對邊與鄰邊之比是定值；當銳角變化時，角的對邊與鄰邊之比也隨之發生變化.這樣滲透了函數思想，揭示銳角三角比是三角函數的基礎，滲透從一般到特殊、從特殊到一般的數學思想方法.緊接著引導學生根據確定三角形的條件，結合全等三角形判定，探究給定什么條件時，可以求解三角形的其他元素？如何求解非直角三角形？從學科角度來看，解三角形問題面對的是一個幾何對象，所以，在此過程中，注重引導學生從數形兩個角度去理解，做到數形的自然融合，體會幾何直觀和代數運算之間的關系.

設計意圖：本節課的重點是需要引導學生從特殊走向一般，得出解任意三角形的方法.

4 結論

總之，課堂上主題化跨單元教學活動的組織和開展，對優化教學內容、發揮學科育人功能、提高學生知識整合能力等方面有著突出的作用.對于教師而言，能夠促進其吃透教材、數學理論，明確各個單元之間的內在聯系，從而在數學課堂上做到游刃有余；對于學生而言，主題化跨單元教學設計，能將不同單元內容合成一個整體，有利于促進他們對知識的整體構建，觸發探究靈感，強化感知能力和綜合學習能力，高效實現對學生進行數學核心素養培育的目標.