通過一題多解 培養關鍵能力*

?福建省泉州師范學院附屬中學 莊惠強

1 引言

教育部于2022年4月頒布的《義務教育數學課程標準(2022年版)》(以下簡稱《新課標》)指出：初中數學核心素養的主要表現包括運算能力、幾何直觀與空間觀念等.運算能力方面要求學生能選擇合理簡潔的運算策略解決問題,通過運算促進數學推理能力的發展[1].

“關鍵能力”指的是學生在運用知識解決問題的過程中所需要的主要學科能力,包括邏輯推理能力、運算求解能力、直觀想象能力、數學建模能力和創新能力五個方面[2].在培養五大關鍵能力的過程中,針對不同的素材,教師要有所側重.本文中結合一題多解案例,闡述如何培養學生運算求解能力.

2 通過一題多解培養學生關鍵能力的案例解析

2.1 案例呈現

如圖1,已知AB=8,點P是線段AB上的一個動點,分別以AP，BP為邊,在線段AB的同側作菱形APCD和菱形PBFE,點P,C,E在同一條直線上,∠DAP=60°,M，N分別是對角線AC，BE的中點,當點P在線段AB上移動時,求點M，N之間距離的最小值.

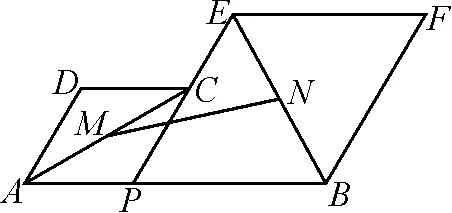
圖1

2.2 培養學生關鍵能力的解析

2.2.1 提升整體思維,培養學生用數學眼光觀察世界 教師要時時刻刻、事事處處站在系統的高度講授知識,讓知識總是以“系統中的知識”的面目出現在學生面前[3].

教師要提升學生的整體思維,概括解題的一般方法,幫助學生積累基本活動經驗.當學生具備解題的基本活動經驗,就能高屋建瓴、整體把握主要矛盾,用數學的眼光觀察問題.初中階段,與計算線段長度或角的度數相關的的通性通法如圖2所示，包括四種情況.

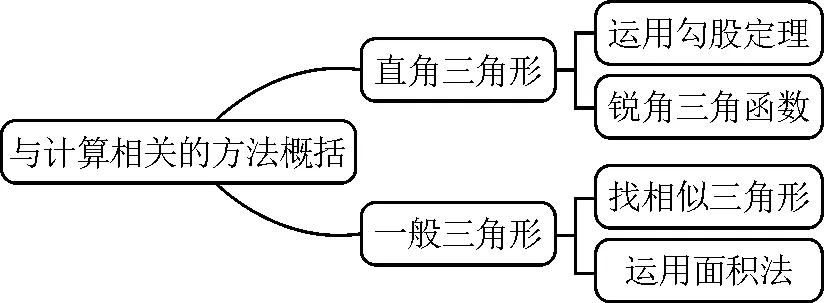
圖2

通過數學的眼光,可以從現實世界的客觀現象中發現數量關系與空間形式, 提出有意義的數學問題；能夠抽象出數學的研究對象及其屬性,形成概念、關系與結構；形成對數學的好奇心與想象力,主動參與數學探究活動, 發展創新意識[1].

本案例中,線段MN是一條獨立的線段,要計算它的長度,通性方法沒有用武之地.從整體眼光來看,把線段MN“置于三角形中”,就能運用以上四種方法計算,因此把眼光重點放在如何構造三角形上.這種結構化思維,能幫助學生撥去迷霧,理清思路.

2.2.2 揭示思維過程,培養學生用數學思維思考世界 在義務教育階段,數學思維主要表現為運算能力、推理意識或推理能力.數學的思維體現為能根據已知事實或原理,合乎邏輯地推出結論,構建數學的邏輯體系；能夠運用符號運算、形式推理等數學方法,分析、解決數學問題和實際問題[1].

(1)加強通性意識,揭示思維過程

因為直角三角形的角與角、邊與邊、邊與角的關系非常穩固,方便計算邊的長度或角的大小,所以首選構造直角三角形.

解法一：如圖3,分別過點M，N作MG⊥AB，NH⊥AB,垂足為G，H,過點M作MI⊥NH于點I.

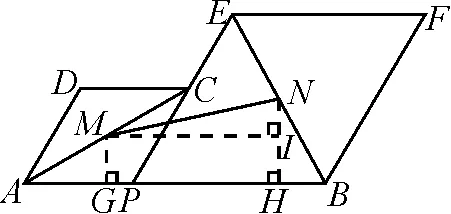
圖3

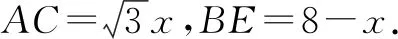
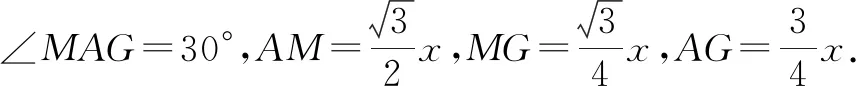
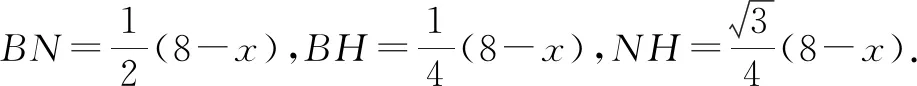
在Rt△MIN中,因為∠MIN=90°,且

所以，可得

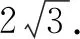
這種思維完全符合學生的認知水平,符合學生的“最近發展區”,學生容易接受、易于找到思維的入口,從“獨立”到“聯系”，化“未知”為“已知”.把線段的長度“置于三角形中”計算,這種思維增強了學生的整體意識,教會學生結構化思維.

(2)梳理解法聯系,尊重思維差異

教師要著眼于知識間的聯系和規律,使學生從系統的高度去把握知識,進行思考,做到八方聯系,渾然一體[3].

解法一是通性通法,優點是容易“切題”,缺點是要作三條輔助線、結構復雜、計算量大.留給學生充足的時間,讓學生展開討論交流,學生的思維差異就會顯現出來.

如圖4,連結MP，NP.因為∠APC+∠BPE=180°,又易得MP是∠APC的角平分線,NP是∠BPE的角平分線,所以∠MPN=90°,即△MPN是直角三角形.與解法一相比,雖然都是構造直角三角形,但是用這種方法構造的直角三角形,圖形簡潔,結構簡單,計算容易,其優越性不言而喻.善于發現并挖掘圖形的特殊特征,是學生學會“數學的思維”的體現,通過計算將已知條件約簡,把條件向前推進一大步,經歷數學“再發現”的過程,發展學生的批判性思維.

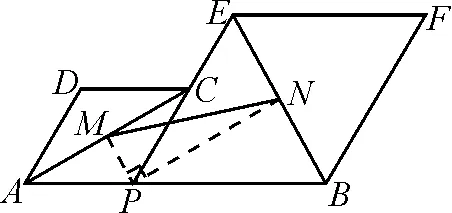
圖4

解法二：如圖4，連結MP，NP,則PM⊥AC，PN⊥BE.

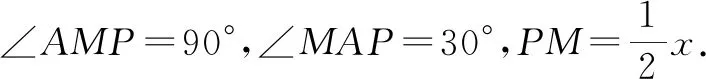
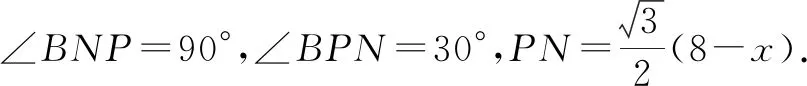
所以，在Rt△MPN中,由∠MPN=90°,可得

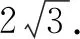
挖掘圖形的特征,找出題目的“個性”,推導出更進一步的結論,為后續的運算求解打下基礎.要尊重學生的思維差異,對于有奇思妙想的學生要給予充分的肯定,對于常規思維的學生,也要給予鼓勵,肯定他們思維的價值,培養他們的學習信心.

2.2.3 領悟數學模型,培養學生用數學語言表達世界 初中階段,數學語言主要表現為模型意識、模型觀念和應用意識.引導學生構造三角形的中位線模型,讓學生從通性通法轉化到數學模型.

根據布魯姆認知理論,回憶、理解與應用屬于低階思維,分析、評價與創造屬于高階思維.本案例中點M，N分別是兩條線段的中點,讓人自然聯想到構造數學模型——三角形的中位線.但是線段MN卻不在一個三角形中,沒辦法直接利用三角形中位線的性質解題.連結PD，PF,根據菱形的性質,對角線的中點也是對角線的交點,構造△PDF,則線段MN是△PDF的中位線,這種思維屬于高階思維的范疇.

如圖5,連結PD，PF.因為M，N分別是對角線AC，BE的中點,所以點P，M，D三點共線,點P，N，F三點共線.

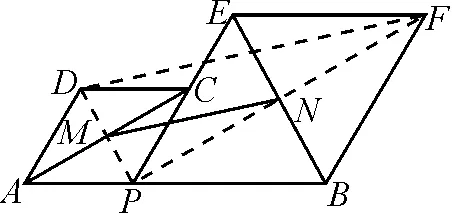
圖5

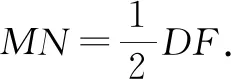
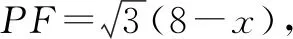
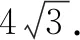
空間觀念有助于理解物體的形態與結構,根據物體之間的位置關系,感知并描述圖形的運動和變化規律.幾何直觀體現在能根據圖形的特征,數形結合構建直觀模型,把握問題的本質,明晰思維的路徑[1].

3 一題多解培養學生關鍵能力的策略

培養學生的關鍵能力，鼓勵多種解法,發展思維的流暢性；鏈接不同解法,啟發思維的靈活性；鼓勵自創解法,促進思維的獨特性[4].基本策略概括如下.

(1)注重提升整體觀念,讓學生擁有數學的眼光

解題教學應該強調通性通法,找出具有相同性質題目解法的“最大公因數”,即尋找解題的“共性”,讓學生解題時有“法”可依、有“章”可循.通過解題提升學生的整體觀念,幫助學生總結運算求解過程中常用的方法,幫助學生尋找解題的一般路徑.解題過程貌似只是考查個別題目的解法,實則是考驗學生對知識的總體把握.厘清概念,準確運用運算法則,迅速找到解題方向、理清解題思路,熟練應用解題技巧,讓學生擁有數學的眼光.

(2)注重把握特殊性質,讓學生擁有數學的思維

林崇德先生認為：思維品質包括敏捷性、靈活性、創造性、批判性與深刻性[5].在強調通性通法的同時,也應該培養學生準確捕捉信息的能力,如代數式之間的聯系、幾何圖形中隱含特殊的性質,都可能為解題提供良好的切入點,讓學生從“有聯系的程序”入手,發展到“做數學”.這是一個從“共性”的總體指導,到尋找題目“個性”的過程,在這個過程中,主要就是引導學生“有邏輯地思考”,培養良好的思維品質,從而讓學生擁有數學的思維.

(3)注重數學思想指導,讓學生擁有數學的語言

數學的解題,離不開數學思想的指引,方程思想、函數思想、模型思想、數形結合思想等能讓學生擁有科學的指導思想.如，數形結合是學生解題最重要的方法之一,“數缺形時少直觀,形缺數時難入微”,數形結合,能夠讓學生實現圖形語言、符號語言與數學語言的熟練切換.模型思想,能讓學生建構獨特的知識體系,讓學生更好地解題.因此，應培養學生的模型思想、應用意識,讓學生擁有數學的語言.

4 結束語

解題教學與知識教學不同,主要按運用已有的知識體系解決問題的數學范式進行[6].這種范式要求學生有大局觀，能把握“共性”,又要細致入微把握事物的“個性”,在數學思想的指導下進行發散性思維,在基本活動經驗的幫助下提高解決問題的能力.

教學的本質就是教會學生學會思維.通過一題多解,教師講課可以做到“少而精”,學生練習“時間足、手段廣”,在提高學生運算求解能力的同時,也會帶動邏輯推理能力、直觀想象能力、數學建模能力與創新能力的提高,從而全面培養學生的數學關鍵能力.